人教版 八年级上册 13.3.2等边三角形专项训练 无答案
文档属性
| 名称 | 人教版 八年级上册 13.3.2等边三角形专项训练 无答案 |
|
|
| 格式 | zip | ||
| 文件大小 | 148.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-07 00:00:00 | ||
图片预览

文档简介
等边三角形专题训练
一、等边三角形与角度计算专题
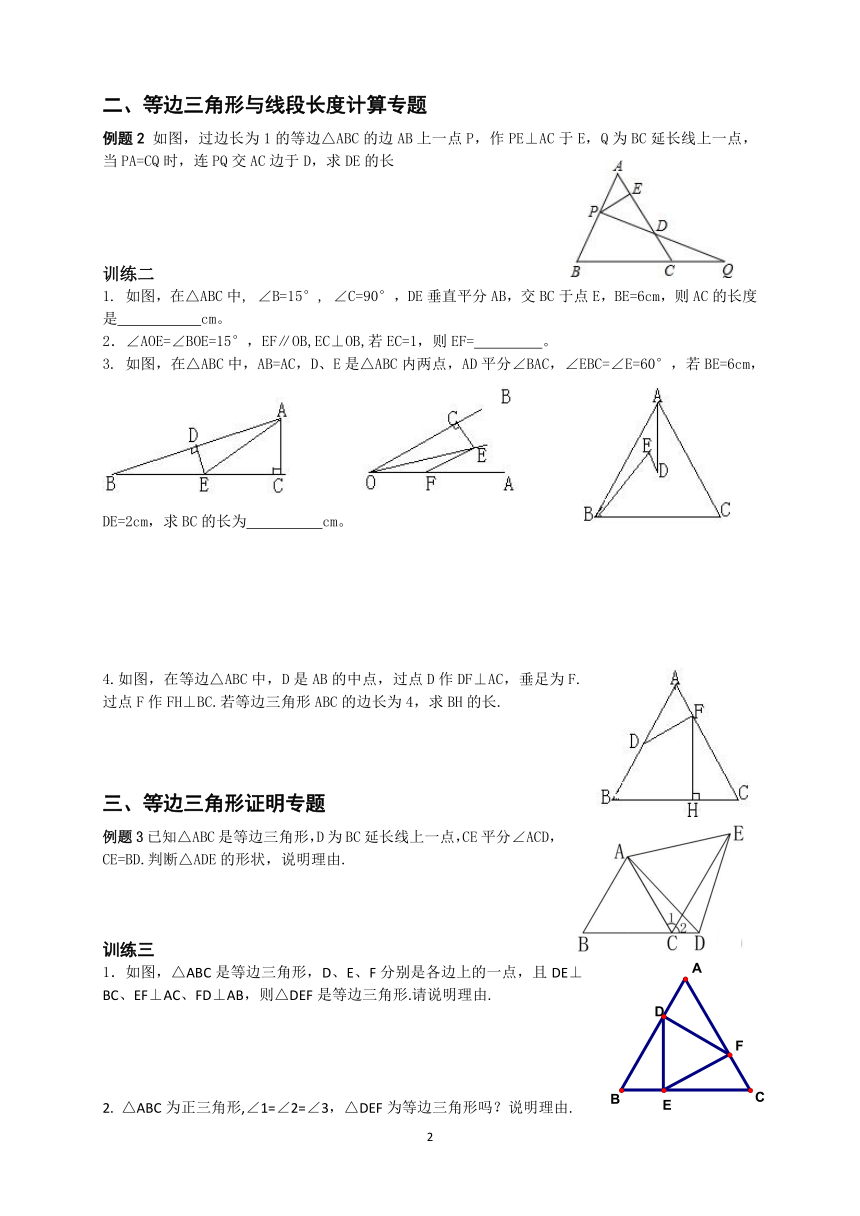
例题1如图,△ABC为等边三角形,且CD=AE,AD与BE相交于点P。
(1)求∠APN的度数;(2)探索BP与PQ的数量关系。
训练一
1.如图,△ABC是等边三角形,点B、C、D、E在一条直线上,且CG=CD,DF=DE,则∠E= 。
2.如图,D为等边三角形ABC内一点,BD=DA,BE=AB,∠DBE=∠DBC,则∠BED的度数为 。
3.如图,C为线段AB上一点,在AB的同侧作等边△ACM和等边△BCN,连接AN、BM,若∠MBN=40°,则∠ANB的大小是 ( )
A 60 B 65 C 70 D 80
4.(2008年广东)(1)如图4,点O是线段AD的中点,分别以AO和DO为边在线段AD的同侧作等边三角形OAB和等边三角形OCD,连结AC和BD,相交于点E,连结BC.求∠AEB的大小;
(2)如图5,ΔOAB固定不动,保持ΔOCD的形状和大小不变,将ΔOCD绕着点O旋转(ΔOAB和ΔOCD不能重叠),求∠AEB的大小.
二、等边三角形与线段长度计算专题
例题2 如图,过边长为1的等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,当PA=CQ时,连PQ交AC边于D,求DE的长
训练二
1. 如图,在△ABC中, ∠B=15°, ∠C=90°,DE垂直平分AB,交BC于点E,BE=6cm,则AC的长度是 cm。
2.∠AOE=∠BOE=15°,EF∥OB,EC⊥OB,若EC=1,则EF= 。
3. 如图,在△ABC中,AB=AC,D、E是△ABC内两点,AD平分∠BAC,∠EBC=∠E=60°,若BE=6cm,DE=2cm,求BC的长为 cm。
4.如图,在等边△ABC中,D是AB的中点,过点D作DF⊥AC,垂足为F.过点F作FH⊥BC.若等边三角形ABC的边长为4,求BH的长.
三、等边三角形证明专题
例题3已知△ABC是等边三角形,D为BC延长线上一点,CE平分∠ACD,CE=BD.判断△ADE的形状,说明理由.
训练三
1.如图,△ABC是等边三角形,D、E、F分别是各边上的一点,且DE⊥BC、EF⊥AC、FD⊥AB,则△DEF是等边三角形.请说明理由.
2. △ABC为正三角形,∠1=∠2=∠3,△DEF为等边三角形吗?说明理由.
3. 如图,△ABC是等边三角形,D是AB边上的一点,以CD为边作等边三角形CDE,使点E、A在直线DC的同侧,连结AE。
求证:AE∥BC
四、等边三角形综合专题
例题4 .如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正三角形ABC和正三角形CDE,AD与BE交于点O.设AD与BC交于点P,BE与CD交于点Q,连接PQ、以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤∠AOB=60°⑥OC平分∠AOE.恒成立的结论有哪些?并证明你的结论。
训练四
1.如图,等边△ABD和等边△CBD的长均为a,现把它们拼合起来,E是AD上异于A、D两点的一动点,F是CD上一动点,满足AE+CF=a.
(1)E、F移动时,△BEF的形状如何
(2)当E、F运动到什么位置时,△BEF面积的最小?
2. (2012 遵义)如图,△ABC是边长为6的等边三角形,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一点,与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,连接PQ交AB于D.
(1)当∠BQD=30°时,求AP的长;
(2)当运动过程中线段ED的长是否发生变化?如果不变,求出线段ED的长;如果变化请说明理由.
3.如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC= α.将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.
(1)求证:△COD是等边三角形;
(2)当α=150°时,试判断△AOD的形状,并说明理由;
(3)探究:当α为多少度时,△AOD是等腰三角形?
五、线段之和最小值专题
例题5 (1)两点一线的最值问题
如图,草原上两居民点A,B在笔直河流l的同旁,一汽车从A处出发到B处,途中需要到河边加水,问选在何处加水可使行驶的路程最短?并在图中画出这一点
(2)两点两线的最值问题
如图A点为马厩,B点为帐篷,牧马人一天要从马厩牵出马,先到草地边某一点牧马,然后到河边去饮水,再回到帐篷,请你确定一天的最短路程。
(3)一点两线的最值问题
如图,点A是总邮局,想在公路MN上建一分局B,在公路EF上建一分局C,使得AB+AC+BC的和最小。
训练五
如图,四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使△AMN周长最小时,则∠AMN+∠ANM的度数为 ( )
A.130° B.120° C.110° D.100°
图5
E
C
A
C
B
D
O
A
B
O
D
PAGE
1
一、等边三角形与角度计算专题
例题1如图,△ABC为等边三角形,且CD=AE,AD与BE相交于点P。
(1)求∠APN的度数;(2)探索BP与PQ的数量关系。
训练一
1.如图,△ABC是等边三角形,点B、C、D、E在一条直线上,且CG=CD,DF=DE,则∠E= 。
2.如图,D为等边三角形ABC内一点,BD=DA,BE=AB,∠DBE=∠DBC,则∠BED的度数为 。
3.如图,C为线段AB上一点,在AB的同侧作等边△ACM和等边△BCN,连接AN、BM,若∠MBN=40°,则∠ANB的大小是 ( )
A 60 B 65 C 70 D 80
4.(2008年广东)(1)如图4,点O是线段AD的中点,分别以AO和DO为边在线段AD的同侧作等边三角形OAB和等边三角形OCD,连结AC和BD,相交于点E,连结BC.求∠AEB的大小;
(2)如图5,ΔOAB固定不动,保持ΔOCD的形状和大小不变,将ΔOCD绕着点O旋转(ΔOAB和ΔOCD不能重叠),求∠AEB的大小.
二、等边三角形与线段长度计算专题
例题2 如图,过边长为1的等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,当PA=CQ时,连PQ交AC边于D,求DE的长
训练二
1. 如图,在△ABC中, ∠B=15°, ∠C=90°,DE垂直平分AB,交BC于点E,BE=6cm,则AC的长度是 cm。
2.∠AOE=∠BOE=15°,EF∥OB,EC⊥OB,若EC=1,则EF= 。
3. 如图,在△ABC中,AB=AC,D、E是△ABC内两点,AD平分∠BAC,∠EBC=∠E=60°,若BE=6cm,DE=2cm,求BC的长为 cm。
4.如图,在等边△ABC中,D是AB的中点,过点D作DF⊥AC,垂足为F.过点F作FH⊥BC.若等边三角形ABC的边长为4,求BH的长.
三、等边三角形证明专题
例题3已知△ABC是等边三角形,D为BC延长线上一点,CE平分∠ACD,CE=BD.判断△ADE的形状,说明理由.
训练三
1.如图,△ABC是等边三角形,D、E、F分别是各边上的一点,且DE⊥BC、EF⊥AC、FD⊥AB,则△DEF是等边三角形.请说明理由.
2. △ABC为正三角形,∠1=∠2=∠3,△DEF为等边三角形吗?说明理由.
3. 如图,△ABC是等边三角形,D是AB边上的一点,以CD为边作等边三角形CDE,使点E、A在直线DC的同侧,连结AE。
求证:AE∥BC
四、等边三角形综合专题
例题4 .如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正三角形ABC和正三角形CDE,AD与BE交于点O.设AD与BC交于点P,BE与CD交于点Q,连接PQ、以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤∠AOB=60°⑥OC平分∠AOE.恒成立的结论有哪些?并证明你的结论。
训练四
1.如图,等边△ABD和等边△CBD的长均为a,现把它们拼合起来,E是AD上异于A、D两点的一动点,F是CD上一动点,满足AE+CF=a.
(1)E、F移动时,△BEF的形状如何
(2)当E、F运动到什么位置时,△BEF面积的最小?
2. (2012 遵义)如图,△ABC是边长为6的等边三角形,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一点,与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,连接PQ交AB于D.
(1)当∠BQD=30°时,求AP的长;
(2)当运动过程中线段ED的长是否发生变化?如果不变,求出线段ED的长;如果变化请说明理由.
3.如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC= α.将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.
(1)求证:△COD是等边三角形;
(2)当α=150°时,试判断△AOD的形状,并说明理由;
(3)探究:当α为多少度时,△AOD是等腰三角形?
五、线段之和最小值专题
例题5 (1)两点一线的最值问题
如图,草原上两居民点A,B在笔直河流l的同旁,一汽车从A处出发到B处,途中需要到河边加水,问选在何处加水可使行驶的路程最短?并在图中画出这一点
(2)两点两线的最值问题
如图A点为马厩,B点为帐篷,牧马人一天要从马厩牵出马,先到草地边某一点牧马,然后到河边去饮水,再回到帐篷,请你确定一天的最短路程。
(3)一点两线的最值问题
如图,点A是总邮局,想在公路MN上建一分局B,在公路EF上建一分局C,使得AB+AC+BC的和最小。
训练五
如图,四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使△AMN周长最小时,则∠AMN+∠ANM的度数为 ( )
A.130° B.120° C.110° D.100°
图5
E
C
A
C
B
D
O
A
B
O
D
PAGE
1
