人教版八年级上册 13.3.2 等边三角形(第一课时)课件(共27张PPT)
文档属性
| 名称 | 人教版八年级上册 13.3.2 等边三角形(第一课时)课件(共27张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-07 21:36:52 | ||
图片预览




文档简介
(共27张PPT)
八年级上册数学 第十三章 轴对称
13.3.2 等边三角形
名称 图 形 定 义 性质与边角关系 判定与边角关系
等
腰
三
角
形
A
B
C
有两条边相等的三角形是等腰三角形.
2.等边对等角.
3. “三线合一”.
4.是轴对称图形. (1条对称轴)
2.等角对等边.
1.两条边相等.
1.两腰相等.
温故知新
等边三角形定义:三条边都相等的三角形叫做等边
三角形.
(正三角形)
等边三角形是特殊的等腰三角形.
我们前面学习三角形分类时,学过一种特殊的等腰三角形是什么三角形?
1.把等腰三角形的性质用于等边三角形,能得到什么结论?
1.等边三角形的内角都相等吗 为什么
等边三角形性质探索:
A
B
C
已知:AB=AC=BC
求证:∠A= ∠ B=∠C= 60°.
证明: ∵AB=AC.
∴∠B=∠C .(等边对等角)
同理 ∠A=∠C .
∴∠A=∠B=∠C.
∵ ∠A+∠B+∠C=180°,
∴ ∠A= ∠B= ∠C=60 °.
等边三角形的内角都相等,并且每一个内角都等于60°.
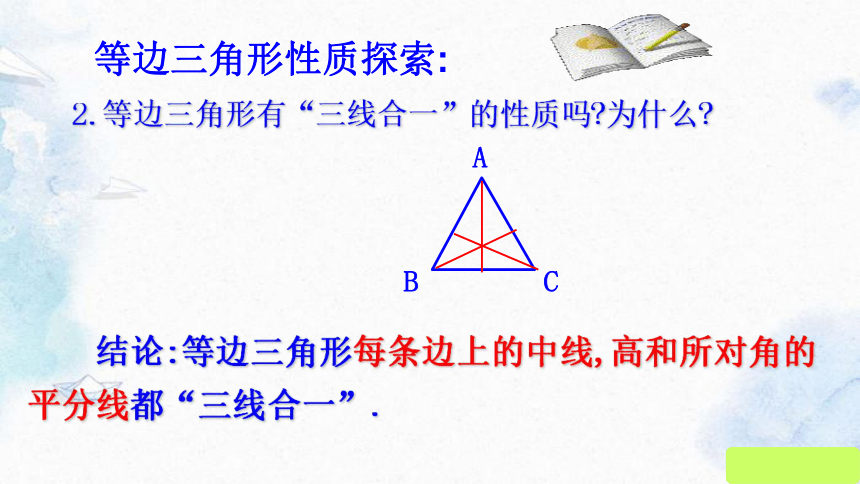
2.等边三角形有“三线合一”的性质吗 为什么
结论:等边三角形每条边上的中线,高和所对角的平分线都“三线合一”.
等边三角形性质探索:
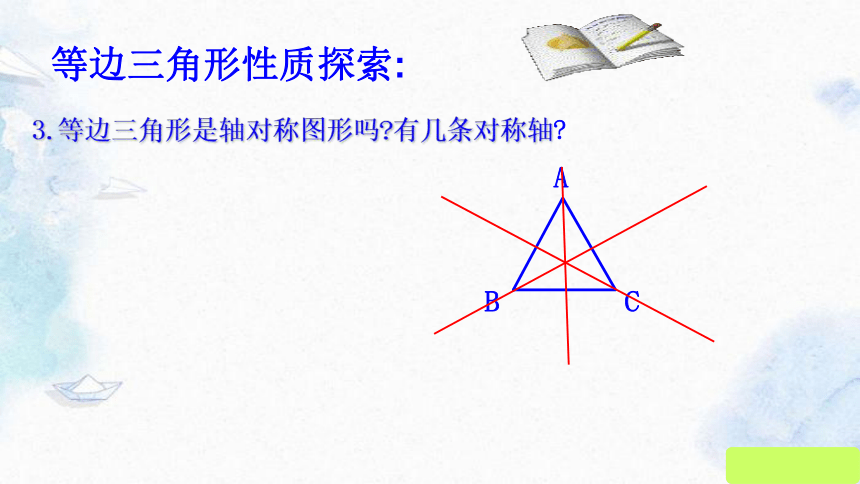
3.等边三角形是轴对称图形吗 有几条对称轴
等边三角形性质探索:
名称 图 形 性质与边角关系
等
边
三
角
形
等边三角形的性质:
2.三个角都相等,且都为60°.
3.“三线合一”.
1.三条边都相等.
4.是轴对称图形,有三条对称轴.
思考题
?
2.一个三角形满足什么条件
就是等边三角形
已知:如图,⊿ABC中, ∠ A=∠B=∠C.
求证:AB=AC=BC.
A
B
C
证明:在⊿ABC中,
∵ ∠ A=∠B(已知),
∴BC=CA(等角对等边).
同理 CA=AB.
∴BC=CA=AB.
⒈ 三个角都相等的三角形是等边三角形吗?
等边三角形判定探索:
问题:如果一个等腰三角形中有一个角是60°,那么这个三角形是什么三角形?
第一种情况:当顶角是600时.
第二种情况:当底角是600时.
分类讨论:
等边三角形判定探索:
有一个内角是60 °的等腰三角形是什么三角形?
假若AB=AC,则∠ B= ∠ C.
1.当顶角∠A=60 °时,∠ B= ∠ C= 60 °.
∴ ∠A= ∠ B= ∠ C=60 °.
∴ △ABC是等边三角形.
2.当底角∠ B= 60时,∠ C=60 °,
∠A=180 -(60 °+60 °)=60. °
∴ ∠A= ∠ B= ∠ C=60 °.
∴ △ABC是等边三角形.
A
B
C
等边三角形判定探索:
等边三角形判定方法:
有一个角是60 °的等腰三角形是等边三角形.
名称 图 形 判定与边角关系
等
边
三
角
形
等边三角形的判定:
2.三个角都相等的三角形.
1.三条边都相等的三角形.
3.有一个角是60°的等腰三角形.
例4,课本(P80),如图:△ABC是等边三角形,DE//BC,分别交AB,AC于点D,E点.
求证:△ADE是等边三角形.
A
D
E
B
C
证明:
∵△ABC是等边三角形,
∵DE∥BC,
∴∠A=∠B=∠C.
∴ ∠ADE=∠B, ∠AED=∠C.
∴ ∠A=∠ADE=∠AED.
∴ △ ADE是等边三角形.
想一想,本题还有
其他证法吗?
D
60 °
60 °
60 °
60 °
60 °
C
A
B
E
在等边三角形ABC中,若DE // BC,分别交AB,AC于点D,E点.
则△ADE是什么
三角形?
△ADE是等边三角形.
A
D
E
B
C
延伸:(小组合作探究)已知: △ABC是等边三角形
(1)如中图:当DE // BC时,若点D、E分别在AB、AC的延长线上,结论依然成立吗?
(2)如右图:当DE // BC时,若点D、E分别在AB、AC的反向延长线上,结论依然成立吗?
例4,课本(P80),如左图:△ABC是等边三角形,DE//BC,分别交AB,AC于点D,E点. 求证:△ADE是等边三角形.
D
E
B
C
A
A
B
C
D
E
1.已知△ABC中,∠A=∠B=60°,AB=3cm, 则 △ABC的周长_______.
2. △ABC是等腰三角形,周长为15cm且∠A=60°,则BC=_______.
9cm
5cm
3.如图,等边三角形ABC中,AD是BC上的高,BDE=∠CDF=60°,
图中有哪些与BD相等的线段?
A
B
E
D
F
C
CD,CF,BE,DE,FD,AF,AE
(P93) 如图,D、E、F分别是等边三角形ABC三边上三点,且AD=BE=CF.
试问:△DEF是什么三角形?
B
E
A
C
D
F
请你说一说这节课的收获和体验,让大家与你一起分享!
等腰三角形 等边三角形
性质 两腰相等
等边对等角
“三线合一”
(底边上的中线、高线、 顶角的角平分线)
4.是轴对称图形(1条对称轴)
三条边相等
三个角相等(都为600 )
“三线合一”
(每条边上的中线、高线、对角的角平分线)
4.是轴对称图形(3条对称轴)
判定 1、定义(两条边相等)
2、等角对等边 1、定义(三条边相等)
2、三个角相等
3、有一个角是600 的等腰三角形
比一比
等边三角形是一种特殊的等腰三角形,你能述说等边三角形与等腰三角形在定义,性质和判定的异同吗
(1)习题13.3(P83)
基础题: 12题
提高题: 14题
(2)本课练习册习题
课后作业
不经历风雨,怎能见彩虹!
没有人能随随便便成功!
谢谢指导,再见!
名称 图 形 概 念 性质与边角关系 判 定
等
边
三
角
形
三边都相等的三角形是等边三角形.
2.三个角都相等,且都为60°.
3. 三线合一.
4.是轴对称图形.
(3条对称轴)
2.三个角都相等.
1.三条边相等.
1.三条边相等.
3.有一个角是60°
的等腰三角形.
等边三角形
B
A
C
D
将两个含有30°的三角尺如图摆放在
一起.你能借助这个图形,找到Rt△ABC的直
角边BC与斜边AB之间的数量关系吗
探究
∵△ABC与△ADC关于AC
成轴对称,
∴AB=AD,
∠BAD =2 ∠BAC= 600.
∴ △ABD是等边三角形.
(有一个角是60°的等腰三角形是
等边三角形)
即AB=AD=BD.
又∵AC⊥BD,
∴BC=DC= 1/2BD= 1/2AB.
B
A
C
D
解:
你能找出Rt△ABC的直角边BC与斜边AB之间的数量关系吗
在直角三角形中,如果一个锐角等于30°,
那么它所对的直角边等于斜边的一半.
A
┓
)
30°
B
C
∵在Rt△ABC中,∠ A=30°,
∴BC= 1/2AC(或 AC=2BC)。
下图是屋架设计图的一部分,点D是
斜梁AB的中点,立柱BC、 DE垂直于
横梁AC,AB=7.4m,∠A=30°.立柱
BC 、 DE要多长
A
B
D
E
C
解:∵DE⊥AC, BC⊥AC, ∠A=30°
∴ BC=1/2 × AB, DE= 1/2 × AD
∴BC=1/2 ×7.4=3.7m
又 AD=1/2 × AB
∴DE=1/2 × AD=1/2 ×3.7=1.85m
答:立柱BC的长是3.7m,
DE的长是1.85m.
A
B
D
E
C
点D是斜梁AB的中点,立柱BC、 DE垂直于横梁AC,AB=7.4m,∠A=30°,立柱BC 、 DE要多长
八年级上册数学 第十三章 轴对称
13.3.2 等边三角形
名称 图 形 定 义 性质与边角关系 判定与边角关系
等
腰
三
角
形
A
B
C
有两条边相等的三角形是等腰三角形.
2.等边对等角.
3. “三线合一”.
4.是轴对称图形. (1条对称轴)
2.等角对等边.
1.两条边相等.
1.两腰相等.
温故知新
等边三角形定义:三条边都相等的三角形叫做等边
三角形.
(正三角形)
等边三角形是特殊的等腰三角形.
我们前面学习三角形分类时,学过一种特殊的等腰三角形是什么三角形?
1.把等腰三角形的性质用于等边三角形,能得到什么结论?
1.等边三角形的内角都相等吗 为什么
等边三角形性质探索:
A
B
C
已知:AB=AC=BC
求证:∠A= ∠ B=∠C= 60°.
证明: ∵AB=AC.
∴∠B=∠C .(等边对等角)
同理 ∠A=∠C .
∴∠A=∠B=∠C.
∵ ∠A+∠B+∠C=180°,
∴ ∠A= ∠B= ∠C=60 °.
等边三角形的内角都相等,并且每一个内角都等于60°.
2.等边三角形有“三线合一”的性质吗 为什么
结论:等边三角形每条边上的中线,高和所对角的平分线都“三线合一”.
等边三角形性质探索:
3.等边三角形是轴对称图形吗 有几条对称轴
等边三角形性质探索:
名称 图 形 性质与边角关系
等
边
三
角
形
等边三角形的性质:
2.三个角都相等,且都为60°.
3.“三线合一”.
1.三条边都相等.
4.是轴对称图形,有三条对称轴.
思考题
?
2.一个三角形满足什么条件
就是等边三角形
已知:如图,⊿ABC中, ∠ A=∠B=∠C.
求证:AB=AC=BC.
A
B
C
证明:在⊿ABC中,
∵ ∠ A=∠B(已知),
∴BC=CA(等角对等边).
同理 CA=AB.
∴BC=CA=AB.
⒈ 三个角都相等的三角形是等边三角形吗?
等边三角形判定探索:
问题:如果一个等腰三角形中有一个角是60°,那么这个三角形是什么三角形?
第一种情况:当顶角是600时.
第二种情况:当底角是600时.
分类讨论:
等边三角形判定探索:
有一个内角是60 °的等腰三角形是什么三角形?
假若AB=AC,则∠ B= ∠ C.
1.当顶角∠A=60 °时,∠ B= ∠ C= 60 °.
∴ ∠A= ∠ B= ∠ C=60 °.
∴ △ABC是等边三角形.
2.当底角∠ B= 60时,∠ C=60 °,
∠A=180 -(60 °+60 °)=60. °
∴ ∠A= ∠ B= ∠ C=60 °.
∴ △ABC是等边三角形.
A
B
C
等边三角形判定探索:
等边三角形判定方法:
有一个角是60 °的等腰三角形是等边三角形.
名称 图 形 判定与边角关系
等
边
三
角
形
等边三角形的判定:
2.三个角都相等的三角形.
1.三条边都相等的三角形.
3.有一个角是60°的等腰三角形.
例4,课本(P80),如图:△ABC是等边三角形,DE//BC,分别交AB,AC于点D,E点.
求证:△ADE是等边三角形.
A
D
E
B
C
证明:
∵△ABC是等边三角形,
∵DE∥BC,
∴∠A=∠B=∠C.
∴ ∠ADE=∠B, ∠AED=∠C.
∴ ∠A=∠ADE=∠AED.
∴ △ ADE是等边三角形.
想一想,本题还有
其他证法吗?
D
60 °
60 °
60 °
60 °
60 °
C
A
B
E
在等边三角形ABC中,若DE // BC,分别交AB,AC于点D,E点.
则△ADE是什么
三角形?
△ADE是等边三角形.
A
D
E
B
C
延伸:(小组合作探究)已知: △ABC是等边三角形
(1)如中图:当DE // BC时,若点D、E分别在AB、AC的延长线上,结论依然成立吗?
(2)如右图:当DE // BC时,若点D、E分别在AB、AC的反向延长线上,结论依然成立吗?
例4,课本(P80),如左图:△ABC是等边三角形,DE//BC,分别交AB,AC于点D,E点. 求证:△ADE是等边三角形.
D
E
B
C
A
A
B
C
D
E
1.已知△ABC中,∠A=∠B=60°,AB=3cm, 则 △ABC的周长_______.
2. △ABC是等腰三角形,周长为15cm且∠A=60°,则BC=_______.
9cm
5cm
3.如图,等边三角形ABC中,AD是BC上的高,BDE=∠CDF=60°,
图中有哪些与BD相等的线段?
A
B
E
D
F
C
CD,CF,BE,DE,FD,AF,AE
(P93) 如图,D、E、F分别是等边三角形ABC三边上三点,且AD=BE=CF.
试问:△DEF是什么三角形?
B
E
A
C
D
F
请你说一说这节课的收获和体验,让大家与你一起分享!
等腰三角形 等边三角形
性质 两腰相等
等边对等角
“三线合一”
(底边上的中线、高线、 顶角的角平分线)
4.是轴对称图形(1条对称轴)
三条边相等
三个角相等(都为600 )
“三线合一”
(每条边上的中线、高线、对角的角平分线)
4.是轴对称图形(3条对称轴)
判定 1、定义(两条边相等)
2、等角对等边 1、定义(三条边相等)
2、三个角相等
3、有一个角是600 的等腰三角形
比一比
等边三角形是一种特殊的等腰三角形,你能述说等边三角形与等腰三角形在定义,性质和判定的异同吗
(1)习题13.3(P83)
基础题: 12题
提高题: 14题
(2)本课练习册习题
课后作业
不经历风雨,怎能见彩虹!
没有人能随随便便成功!
谢谢指导,再见!
名称 图 形 概 念 性质与边角关系 判 定
等
边
三
角
形
三边都相等的三角形是等边三角形.
2.三个角都相等,且都为60°.
3. 三线合一.
4.是轴对称图形.
(3条对称轴)
2.三个角都相等.
1.三条边相等.
1.三条边相等.
3.有一个角是60°
的等腰三角形.
等边三角形
B
A
C
D
将两个含有30°的三角尺如图摆放在
一起.你能借助这个图形,找到Rt△ABC的直
角边BC与斜边AB之间的数量关系吗
探究
∵△ABC与△ADC关于AC
成轴对称,
∴AB=AD,
∠BAD =2 ∠BAC= 600.
∴ △ABD是等边三角形.
(有一个角是60°的等腰三角形是
等边三角形)
即AB=AD=BD.
又∵AC⊥BD,
∴BC=DC= 1/2BD= 1/2AB.
B
A
C
D
解:
你能找出Rt△ABC的直角边BC与斜边AB之间的数量关系吗
在直角三角形中,如果一个锐角等于30°,
那么它所对的直角边等于斜边的一半.
A
┓
)
30°
B
C
∵在Rt△ABC中,∠ A=30°,
∴BC= 1/2AC(或 AC=2BC)。
下图是屋架设计图的一部分,点D是
斜梁AB的中点,立柱BC、 DE垂直于
横梁AC,AB=7.4m,∠A=30°.立柱
BC 、 DE要多长
A
B
D
E
C
解:∵DE⊥AC, BC⊥AC, ∠A=30°
∴ BC=1/2 × AB, DE= 1/2 × AD
∴BC=1/2 ×7.4=3.7m
又 AD=1/2 × AB
∴DE=1/2 × AD=1/2 ×3.7=1.85m
答:立柱BC的长是3.7m,
DE的长是1.85m.
A
B
D
E
C
点D是斜梁AB的中点,立柱BC、 DE垂直于横梁AC,AB=7.4m,∠A=30°,立柱BC 、 DE要多长
