4.2.1 等差数列课件-2021-2022学年高二下学期数学人教A版(2019)选择性必修第二册(共23张PPT)
文档属性
| 名称 | 4.2.1 等差数列课件-2021-2022学年高二下学期数学人教A版(2019)选择性必修第二册(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-07 20:55:30 | ||
图片预览







文档简介
(共23张PPT)
4.2.1 等差数列
2.数列中的每一个数叫做这个数列的项。
各项依次叫做数列的第1项,第2项,···,第n项,
3.数列的分类
(1)按项数分:
项数有限的数列叫有穷数列。
项数无限的数列叫无穷数列。
(2)按项之间的大小关系:
递增数列,
递减数列,
摆动数列,
常数列。
1.数列:
按照确定的顺序排列的一列数。
复习回顾
请看下面几个问题中的数列.
1.北京天坛圜丘坛的地面是由石板铺成,最中间是圆形的天心石,围绕天心石的是9圈扇环形的石板,从内到外的石板数依次为 9,18,27,36,45,54,63,72,81.
情境导入
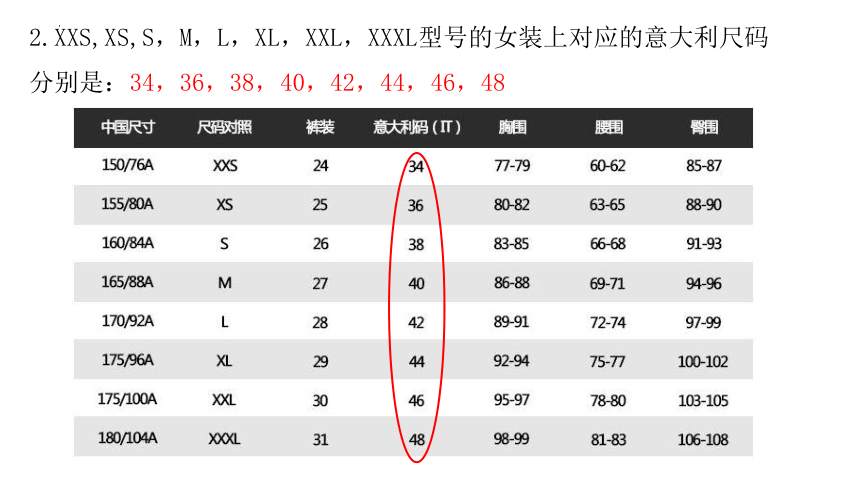
2.XXS,XS,S,M,L,XL,XXL,XXXL型号的女装上对应的意大利尺码分别是:34,36,38,40,42,44,46,48
3.测量某地垂直地面方向上海拔500m以下的大气温度,得到从距离地面20m起每升高100m处的大气温度(单位:℃)依次为
① 9,18,27,36,45,54,63,72,81.
② 38,40,42,44,46,48.
③ 25,24,23,22,21.
对于①,我们发现
18=9+9,27=18+9....81=72+9,
换一种写法,就是
18-9=9,27-18=9....81-72=9.
如果用{an}表示数列①,
那么有a2-a1=9,a3- a2 =9,...a9-a8=9.
问题探究1
什么是等差数列?
思考:你能归纳出等差数列的定义吗?
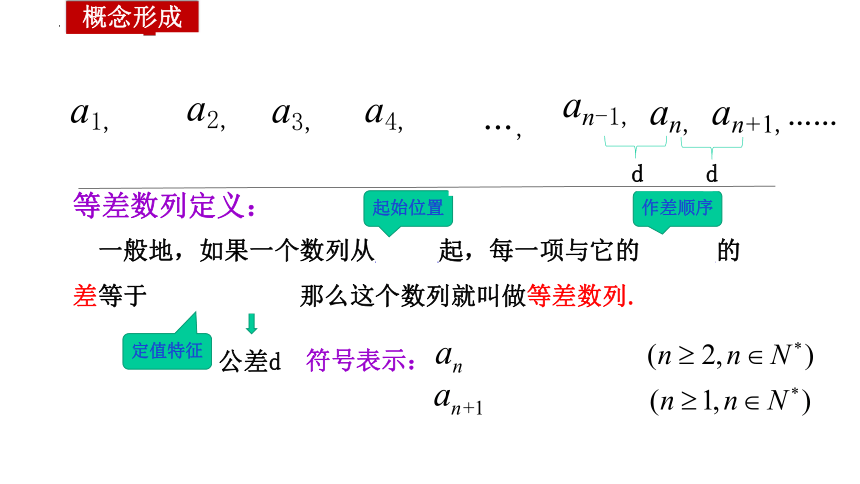
概念形成
等差数列定义:
一般地,如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,那么这个数列就叫做等差数列.
公差d
符号表示:
起始位置
作差顺序
定值特征
a1,
a3,
a4,
an,
an+1,……
…,
d
d
a2,
an-1,
概念辨析
1.判断以下数列是等差数列吗?若是,求出公差。
公差是3
(3)1,1,1,1,1;
公差是0
(2)6,4,2;
公差是-2
(1)4,7,10,13,16;
(4)-3,-2,-1,1,2,3 .
d>0 增数列
d<0 减数列
d=0 常数列
是
是
是
不是
注意:
1. 判断一个数列是不是等差数列,主要是由定义进行判断,即判定an+1-an 是不是同一个常数.
2. 公差d是每一项(从第2项起)与它的前一项的差,而且公差可以是正数,负数,也可以为0.
判断对错:
1. 常数列是等差数列. ( )
2. 若一个数列从第2项起每一项与前一项的差都是常数,则这个数列是等差数列. ( )
3. 数列{an}满足an+1-an=1(n>1),则数列{an}是等差数列. ( )
{an}不一定是等差数列,忽略了第1项.
√
×
×
概念形成
(3)1,1,1,1,1;
(2)6,4,2;
(1)4,7,10,13,16;
(4)-3,-2,-1,1,2,3 .
(1)2008,2012,2016.
(3)48,53,58,63.
(4)28, 21.5, 15, 8.5, 2 ,-4.5.
(2)104.25, 108.5, 112.75, 117,121.25……
由三个数a,A,b组成的等差数列
特点:
由三个数构成
a与b的等差中项.
概念形成
(2)6,4,2;
(1)2008,2012,2016;
由三个数a,A,b组成的等差数列,A为
特点:
由三个数构成
a与b的等差中项.
试一试:在横线填入一个数,让数列成为一个等差数列
(1)2, ,4;(2)-8, ,0;(3)a, ,b
由三个数a,A,b组成的等差数列可以看成是最简单的等差数列,这时A叫做a与b的等差中项.
等差中项
由等差数列的定义,可知
… …
求等差数列1,4,7,10,13,16,…的通项公式
问题探究2
如何求等差数列的通项公式?
问题:如果已知一个等差数列的首项是 a1 ,公差是 d ,那么这个数列的通项an 能求出吗?
所以
由此得到:
问题:如果已知一个等差数列的首项是 a1 ,公差是 d ,那么这个数列的通项an 能求出吗?
分析1:根据等差数列的定义:
不完全归纳
(通项公式)
问题探究2
由此得到:
(通项公式)
分析2:根据等差数列的定义:
累加法
问题探究2
(n ≥ 2)
首项为a1,公差为d的等差数列{an}的通项公式为
等差数列的通项公式的一般形式:an=am+(n-m)d
等差数列的通项公式
a1,an,n,d 知三求一
am=a1 +(m-1)d
an-am =(n-m) d
am=
an-am =
思考
1. 求下列等差数列的通项公式
(1)9,18,27,36,45,54,63,72...
(2)38,40,42,44,46,48...
(3)25,24,23,22,21.
解:(1)an=9+(n-1)×9=9n
(2)an=38+(n-1)×2=2n+36
(3)an=25+(n-1)×(-1)=-n+26
小试牛刀
①公差d≠0的等差数列{an}的图象是点(n,an)组成的集合,这些点均匀分布在直线f(x)=dx+(a1-d)上.
(k+b)
k
an=a1+(n-1)d=dn+(a1-d)
②任给一次函数f(x)=kx+b (k,b为常数),则f(1)=k+b,
f(2)=2k+b, …, f(n)=nk+b,构成一个等差数列{nk+b},
其首项为________,公差为____.
思考 我们知道数列是自变量为n的函数,你认为等差数列与我们熟悉的哪一类函数有关?
等差数列与一次函数的关系
探究新知
1
2
5
a1
x
f(x)
O
3
4
6
a1-d
a2
a3
a4
a5
a6
f(x)=dx+(a1-d)
1
2
a1
x
f(x)
O
3
4
5
6
a1-d
a2
a3
a4
a5
a6
f(x)=dx+(a1-d)
1
2
a6
x
f(x)
O
3
4
5
6
a1-d
a5
a4
a3
a2
a1
f(x)=dx+(a1-d)
结论:当d>0时,数列{an}单调递增; 当d<0时,数列{an}单调递减;当d=0时,等差数列{an}为常数列.
探究:可以从函数的角度,研究等差数列的单调性吗?
探究新知
例1 (1) 已知等差数列{an}的通项公式为an=5-2n,求{an}公差和首项;
(2) 求等差数列 8,5,2,···的第20项.
解: (1)当n≥2时,由{an}的通项公式为an=5-2n,可得
an-1=5-2(n-1) =7-2n.
于是 d=an-an-1=5-2n-(7-2n)=-2, a1=5-2=3.
∴{an}公差为-2,首项为3.
(2) 由已知条件,得 d=5-8=-3,a1=8.
∴an= a1+ (n-1)d =8-3(n-1)=-3n+11.
∴a20 =-3×20+11=-49.
知三求一
典例分析
例2 -401是不是等差数列 -5,-9,-13,…的项?如果是,是第几项?
分析:先求出数列的通项公式,它是一个关于n的方程,再看-401是否能使这个方程有正整数解.
解:由a1=-5,d=-9-(-5)=-4,
所以数列的通项公式为an=-5-4(n-1)=-4n-1.
令-4n-1=-401,解得n=100.
所以,-401是这个数列的项,是第100项。
典例分析
解:(1)a10=a1+9d=2+9×3=29
(2)∵21=3+(n-1)×2 ∴n=10
(3)∵a6=a1+5d,即27=12+5d ∴ d=3
巩固练习
(4)∵a7=a1+6d ,即8=a1+6×( ) ∴a1=10
1.在下列等差数列{an}中,
(1)已知a1=2,d=3,n=10,求a10;
(2)已知a1=3,an=21,d=2,求n;
(3)已知a1=12,a6=27,求d;
(4)已知d= ,a7=8,求a1.
1 等差数列的概念
(1) 等差数列及等差中项的定义;
(2) 等差数列的通项公式;
递推公式、归纳法.
(3) 通项公式的应用.
函数与方程.
2 研究方法
递推公式
应用
通项公式
回顾本节课的探究过程,你学到了什么?
函数与方程
的思想
课堂小结
4.2.1 等差数列
2.数列中的每一个数叫做这个数列的项。
各项依次叫做数列的第1项,第2项,···,第n项,
3.数列的分类
(1)按项数分:
项数有限的数列叫有穷数列。
项数无限的数列叫无穷数列。
(2)按项之间的大小关系:
递增数列,
递减数列,
摆动数列,
常数列。
1.数列:
按照确定的顺序排列的一列数。
复习回顾
请看下面几个问题中的数列.
1.北京天坛圜丘坛的地面是由石板铺成,最中间是圆形的天心石,围绕天心石的是9圈扇环形的石板,从内到外的石板数依次为 9,18,27,36,45,54,63,72,81.
情境导入
2.XXS,XS,S,M,L,XL,XXL,XXXL型号的女装上对应的意大利尺码分别是:34,36,38,40,42,44,46,48
3.测量某地垂直地面方向上海拔500m以下的大气温度,得到从距离地面20m起每升高100m处的大气温度(单位:℃)依次为
① 9,18,27,36,45,54,63,72,81.
② 38,40,42,44,46,48.
③ 25,24,23,22,21.
对于①,我们发现
18=9+9,27=18+9....81=72+9,
换一种写法,就是
18-9=9,27-18=9....81-72=9.
如果用{an}表示数列①,
那么有a2-a1=9,a3- a2 =9,...a9-a8=9.
问题探究1
什么是等差数列?
思考:你能归纳出等差数列的定义吗?
概念形成
等差数列定义:
一般地,如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,那么这个数列就叫做等差数列.
公差d
符号表示:
起始位置
作差顺序
定值特征
a1,
a3,
a4,
an,
an+1,……
…,
d
d
a2,
an-1,
概念辨析
1.判断以下数列是等差数列吗?若是,求出公差。
公差是3
(3)1,1,1,1,1;
公差是0
(2)6,4,2;
公差是-2
(1)4,7,10,13,16;
(4)-3,-2,-1,1,2,3 .
d>0 增数列
d<0 减数列
d=0 常数列
是
是
是
不是
注意:
1. 判断一个数列是不是等差数列,主要是由定义进行判断,即判定an+1-an 是不是同一个常数.
2. 公差d是每一项(从第2项起)与它的前一项的差,而且公差可以是正数,负数,也可以为0.
判断对错:
1. 常数列是等差数列. ( )
2. 若一个数列从第2项起每一项与前一项的差都是常数,则这个数列是等差数列. ( )
3. 数列{an}满足an+1-an=1(n>1),则数列{an}是等差数列. ( )
{an}不一定是等差数列,忽略了第1项.
√
×
×
概念形成
(3)1,1,1,1,1;
(2)6,4,2;
(1)4,7,10,13,16;
(4)-3,-2,-1,1,2,3 .
(1)2008,2012,2016.
(3)48,53,58,63.
(4)28, 21.5, 15, 8.5, 2 ,-4.5.
(2)104.25, 108.5, 112.75, 117,121.25……
由三个数a,A,b组成的等差数列
特点:
由三个数构成
a与b的等差中项.
概念形成
(2)6,4,2;
(1)2008,2012,2016;
由三个数a,A,b组成的等差数列,A为
特点:
由三个数构成
a与b的等差中项.
试一试:在横线填入一个数,让数列成为一个等差数列
(1)2, ,4;(2)-8, ,0;(3)a, ,b
由三个数a,A,b组成的等差数列可以看成是最简单的等差数列,这时A叫做a与b的等差中项.
等差中项
由等差数列的定义,可知
… …
求等差数列1,4,7,10,13,16,…的通项公式
问题探究2
如何求等差数列的通项公式?
问题:如果已知一个等差数列的首项是 a1 ,公差是 d ,那么这个数列的通项an 能求出吗?
所以
由此得到:
问题:如果已知一个等差数列的首项是 a1 ,公差是 d ,那么这个数列的通项an 能求出吗?
分析1:根据等差数列的定义:
不完全归纳
(通项公式)
问题探究2
由此得到:
(通项公式)
分析2:根据等差数列的定义:
累加法
问题探究2
(n ≥ 2)
首项为a1,公差为d的等差数列{an}的通项公式为
等差数列的通项公式的一般形式:an=am+(n-m)d
等差数列的通项公式
a1,an,n,d 知三求一
am=a1 +(m-1)d
an-am =(n-m) d
am=
an-am =
思考
1. 求下列等差数列的通项公式
(1)9,18,27,36,45,54,63,72...
(2)38,40,42,44,46,48...
(3)25,24,23,22,21.
解:(1)an=9+(n-1)×9=9n
(2)an=38+(n-1)×2=2n+36
(3)an=25+(n-1)×(-1)=-n+26
小试牛刀
①公差d≠0的等差数列{an}的图象是点(n,an)组成的集合,这些点均匀分布在直线f(x)=dx+(a1-d)上.
(k+b)
k
an=a1+(n-1)d=dn+(a1-d)
②任给一次函数f(x)=kx+b (k,b为常数),则f(1)=k+b,
f(2)=2k+b, …, f(n)=nk+b,构成一个等差数列{nk+b},
其首项为________,公差为____.
思考 我们知道数列是自变量为n的函数,你认为等差数列与我们熟悉的哪一类函数有关?
等差数列与一次函数的关系
探究新知
1
2
5
a1
x
f(x)
O
3
4
6
a1-d
a2
a3
a4
a5
a6
f(x)=dx+(a1-d)
1
2
a1
x
f(x)
O
3
4
5
6
a1-d
a2
a3
a4
a5
a6
f(x)=dx+(a1-d)
1
2
a6
x
f(x)
O
3
4
5
6
a1-d
a5
a4
a3
a2
a1
f(x)=dx+(a1-d)
结论:当d>0时,数列{an}单调递增; 当d<0时,数列{an}单调递减;当d=0时,等差数列{an}为常数列.
探究:可以从函数的角度,研究等差数列的单调性吗?
探究新知
例1 (1) 已知等差数列{an}的通项公式为an=5-2n,求{an}公差和首项;
(2) 求等差数列 8,5,2,···的第20项.
解: (1)当n≥2时,由{an}的通项公式为an=5-2n,可得
an-1=5-2(n-1) =7-2n.
于是 d=an-an-1=5-2n-(7-2n)=-2, a1=5-2=3.
∴{an}公差为-2,首项为3.
(2) 由已知条件,得 d=5-8=-3,a1=8.
∴an= a1+ (n-1)d =8-3(n-1)=-3n+11.
∴a20 =-3×20+11=-49.
知三求一
典例分析
例2 -401是不是等差数列 -5,-9,-13,…的项?如果是,是第几项?
分析:先求出数列的通项公式,它是一个关于n的方程,再看-401是否能使这个方程有正整数解.
解:由a1=-5,d=-9-(-5)=-4,
所以数列的通项公式为an=-5-4(n-1)=-4n-1.
令-4n-1=-401,解得n=100.
所以,-401是这个数列的项,是第100项。
典例分析
解:(1)a10=a1+9d=2+9×3=29
(2)∵21=3+(n-1)×2 ∴n=10
(3)∵a6=a1+5d,即27=12+5d ∴ d=3
巩固练习
(4)∵a7=a1+6d ,即8=a1+6×( ) ∴a1=10
1.在下列等差数列{an}中,
(1)已知a1=2,d=3,n=10,求a10;
(2)已知a1=3,an=21,d=2,求n;
(3)已知a1=12,a6=27,求d;
(4)已知d= ,a7=8,求a1.
1 等差数列的概念
(1) 等差数列及等差中项的定义;
(2) 等差数列的通项公式;
递推公式、归纳法.
(3) 通项公式的应用.
函数与方程.
2 研究方法
递推公式
应用
通项公式
回顾本节课的探究过程,你学到了什么?
函数与方程
的思想
课堂小结
