解方程(课件)——五年级上册数学 人教版(共18张PPT)
文档属性
| 名称 | 解方程(课件)——五年级上册数学 人教版(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-07 00:00:00 | ||
图片预览





文档简介
(共18张PPT)
第3课时 解方程(1)
第五单元 简易方程
人教版五年级上册
1.使学生初步理解“方程的解”与“解方程”的含义,会检验一个具体值是不是方程的解,掌握检验的格式。
3.经历探索解方程的方法,体验成功,激发学习兴趣。
2.利用等式的性质解简易方程,关注由具体到一般的抽象概括过程,培养学生的代数思想。
【教学目标】
重点:理解“方程的解”和“解方程”的含义。
【重点难点】
难点:理解形如a±x=b的方程原理,
掌握正确的解方程格式及检验方法。
等式的性质1
等式两边加上或减去同一个数,左右两边仍然相等。
等式的性质2
等式两边乘同一个数,或除以同一个不为0的数,左右两边仍然相等。
导入
猜一猜:盒子里有x个球,x可能是哪些数
x表示任意数。
导入
盒子里的个数+3个球=9
x+3=9
x个
9个
x =?
你能根据上图列出方程吗?
新知
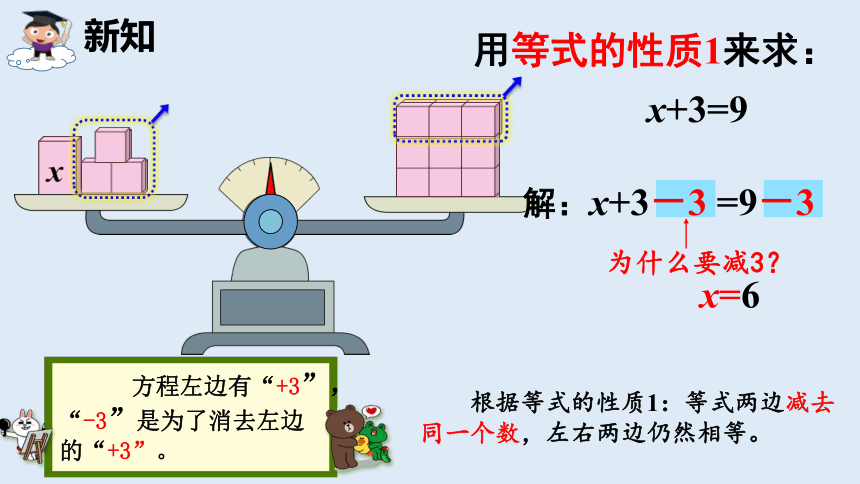
用等式的性质1来求:
x+3=9
x=6
为什么要减3?
解:x+3-3 =9-3
方程左边有“+3”,
“-3”是为了消去左边
的“+3”。
根据等式的性质1:等式两边减去
同一个数,左右两边仍然相等。
新知
x+3 = 9
x+3-3 = 9-3
x = 6
解:
第二行起写解。
等号对齐。
规范解答:
解方程的技巧:
1、先写“解”。
2、然后让方程左边只剩 x,根据等式的性质1,使得方程两边同时加或减去一个相同的数。(也就是遇到加就一起减;遇到减就一起加)
3、之后求出 x的值。
4、最后进行验算。
新知
1、使方程左右两边相等的未知数的值,叫做方程的解。像上面,x=6就是方程x+3=9的解。
2、求方程的解的过程叫做解方程。
x+3 = 9
x = 6
解:
x+3-3 = 9-3
x=6是不是正确的答案呢?检验一下。
=6+3
=9
=方程右边
所以,x=6是方程的解。
方程左边=x+3
新知
1. 解下列方程。
100+ x = 250
解:100+x-100=250-100
x=150
x+12=31
解:x+12-12=31-12
x=19
x-63=36
解:x-63+63=36+63
x=99
为什么加63?
提示:遇到加就一起减;遇到减就一起加。
练习
2. x=2是方程5x=15的解吗?x=3呢?
方程左边=5x
=5×2
=10
≠方程右边
所以, x=2不是方程的解。
方程左边=5x
=5×3
=15
=方程右边
所以, x=3是方程的解。
求出方程的解以后,要养成及时检验的好习惯。不要求检验,也要在心里验算一下。
练习
3. 判断。(对的打“√”,错的打“×”)
(1)求方程的解的过程叫做解方程。 ( )
(2) 12是方程x+4=16的解。 ( )
(3)解方程12+x=28时,方程左右两边要减去12。 ( )
(4) 9=x+4.8不是方程。 ( )
√
×
√
×
练习
4. 解方程并检验。
(1)18+x=32
解: 18+x-18=32-18
x=14
方程左边 =18+x
=18+14
=32
=方程右边
所以,x=14是方程的解。
检验
练习
(2)x-13.4=6.8
解: x-13.4+13.4=6.8+13.4
x=20.2
方程左边 =x-13.4
4. 解方程并检验。
=20.2 -13.4
=6.8
=方程右边
所以,x=20.2是方程的解。
检验
练习
(3)x+6.8=13.6
解: x+6.8-6.8=13.6 -6.8
x=6.8
方程左边 =x+6.8
4. 解方程并检验。
=6.8+6.8
=13.6
=方程右边
所以,x=6.8是方程的解。
检验
练习
(4)x-9=24
解: x-9+9=24+9
x=33
方程左边 =x-9
4. 解方程并检验。
检验
=33-9
=24
=方程右边
所以,x=33是方程的解。
练习
5、列方程表示下面的数量关系,并求出方程的解。
(1)x加上276等于438,求x。
x+276=438
解:x+276-276=438-276
x=162
(2)x减去35.2的差是47.9,求x。
x-35.2=47.9
解: x-35.2+35.2=47.9+35.2
x=83.1
练习
一、解方程的步骤:
1、先写“解”。
2、然后让方程左边只剩 x,根据等式的性质1,使得方程两边同时加或减去一个相同的数。(也就是遇到加就一起减;遇到减就一起加)
3、之后求出 x的值。
4、最后进行验算。
二、使方程左右两边相等的未知数的值,叫做方程的解。像上面,x=6就是方程x+3=9的解。
三、求方程的解的过程叫做解方程。
小结
第3课时 解方程(1)
第五单元 简易方程
人教版五年级上册
1.使学生初步理解“方程的解”与“解方程”的含义,会检验一个具体值是不是方程的解,掌握检验的格式。
3.经历探索解方程的方法,体验成功,激发学习兴趣。
2.利用等式的性质解简易方程,关注由具体到一般的抽象概括过程,培养学生的代数思想。
【教学目标】
重点:理解“方程的解”和“解方程”的含义。
【重点难点】
难点:理解形如a±x=b的方程原理,
掌握正确的解方程格式及检验方法。
等式的性质1
等式两边加上或减去同一个数,左右两边仍然相等。
等式的性质2
等式两边乘同一个数,或除以同一个不为0的数,左右两边仍然相等。
导入
猜一猜:盒子里有x个球,x可能是哪些数
x表示任意数。
导入
盒子里的个数+3个球=9
x+3=9
x个
9个
x =?
你能根据上图列出方程吗?
新知
用等式的性质1来求:
x+3=9
x=6
为什么要减3?
解:x+3-3 =9-3
方程左边有“+3”,
“-3”是为了消去左边
的“+3”。
根据等式的性质1:等式两边减去
同一个数,左右两边仍然相等。
新知
x+3 = 9
x+3-3 = 9-3
x = 6
解:
第二行起写解。
等号对齐。
规范解答:
解方程的技巧:
1、先写“解”。
2、然后让方程左边只剩 x,根据等式的性质1,使得方程两边同时加或减去一个相同的数。(也就是遇到加就一起减;遇到减就一起加)
3、之后求出 x的值。
4、最后进行验算。
新知
1、使方程左右两边相等的未知数的值,叫做方程的解。像上面,x=6就是方程x+3=9的解。
2、求方程的解的过程叫做解方程。
x+3 = 9
x = 6
解:
x+3-3 = 9-3
x=6是不是正确的答案呢?检验一下。
=6+3
=9
=方程右边
所以,x=6是方程的解。
方程左边=x+3
新知
1. 解下列方程。
100+ x = 250
解:100+x-100=250-100
x=150
x+12=31
解:x+12-12=31-12
x=19
x-63=36
解:x-63+63=36+63
x=99
为什么加63?
提示:遇到加就一起减;遇到减就一起加。
练习
2. x=2是方程5x=15的解吗?x=3呢?
方程左边=5x
=5×2
=10
≠方程右边
所以, x=2不是方程的解。
方程左边=5x
=5×3
=15
=方程右边
所以, x=3是方程的解。
求出方程的解以后,要养成及时检验的好习惯。不要求检验,也要在心里验算一下。
练习
3. 判断。(对的打“√”,错的打“×”)
(1)求方程的解的过程叫做解方程。 ( )
(2) 12是方程x+4=16的解。 ( )
(3)解方程12+x=28时,方程左右两边要减去12。 ( )
(4) 9=x+4.8不是方程。 ( )
√
×
√
×
练习
4. 解方程并检验。
(1)18+x=32
解: 18+x-18=32-18
x=14
方程左边 =18+x
=18+14
=32
=方程右边
所以,x=14是方程的解。
检验
练习
(2)x-13.4=6.8
解: x-13.4+13.4=6.8+13.4
x=20.2
方程左边 =x-13.4
4. 解方程并检验。
=20.2 -13.4
=6.8
=方程右边
所以,x=20.2是方程的解。
检验
练习
(3)x+6.8=13.6
解: x+6.8-6.8=13.6 -6.8
x=6.8
方程左边 =x+6.8
4. 解方程并检验。
=6.8+6.8
=13.6
=方程右边
所以,x=6.8是方程的解。
检验
练习
(4)x-9=24
解: x-9+9=24+9
x=33
方程左边 =x-9
4. 解方程并检验。
检验
=33-9
=24
=方程右边
所以,x=33是方程的解。
练习
5、列方程表示下面的数量关系,并求出方程的解。
(1)x加上276等于438,求x。
x+276=438
解:x+276-276=438-276
x=162
(2)x减去35.2的差是47.9,求x。
x-35.2=47.9
解: x-35.2+35.2=47.9+35.2
x=83.1
练习
一、解方程的步骤:
1、先写“解”。
2、然后让方程左边只剩 x,根据等式的性质1,使得方程两边同时加或减去一个相同的数。(也就是遇到加就一起减;遇到减就一起加)
3、之后求出 x的值。
4、最后进行验算。
二、使方程左右两边相等的未知数的值,叫做方程的解。像上面,x=6就是方程x+3=9的解。
三、求方程的解的过程叫做解方程。
小结
