物理人教版(2019)选择性必修第二册2.2电磁感应定律(共24张ppt)
文档属性
| 名称 | 物理人教版(2019)选择性必修第二册2.2电磁感应定律(共24张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-11-07 20:30:23 | ||
图片预览






文档简介
(共24张PPT)
2.2电磁感应定律
用左右手确定方向的电磁学定则
01
法拉第电磁感应定律
02
课后题讲解
03
目录
用左右手确定方向的电磁学定则
ONE
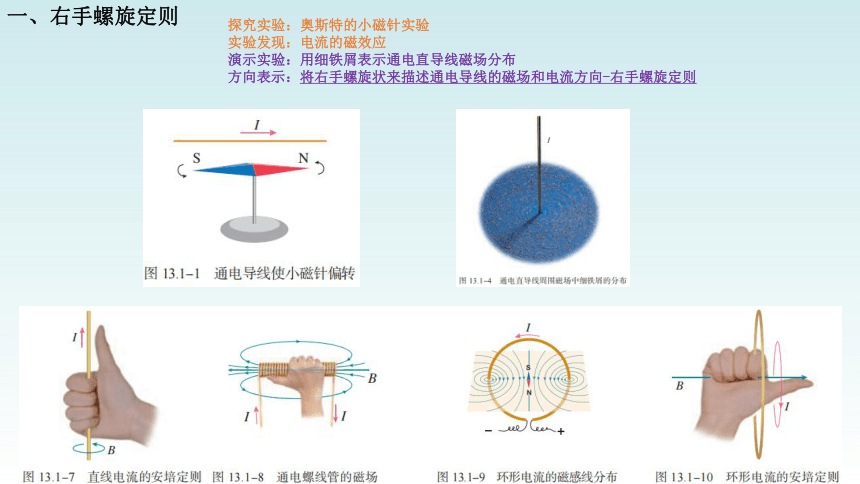
一、右手螺旋定则
探究实验:奥斯特的小磁针实验
实验发现:电流的磁效应
演示实验:用细铁屑表示通电直导线磁场分布
方向表示:将右手螺旋状来描述通电导线的磁场和电流方向-右手螺旋定则
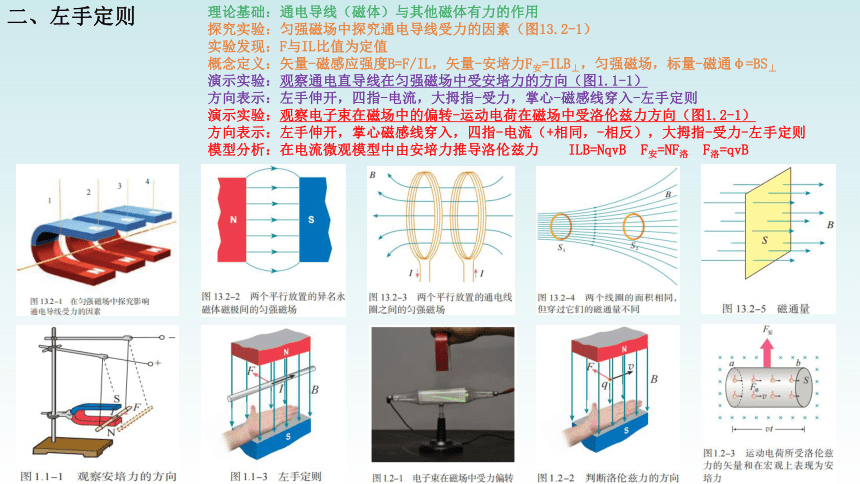
二、左手定则
理论基础:通电导线(磁体)与其他磁体有力的作用
探究实验:匀强磁场中探究通电导线受力的因素(图13.2-1)
实验发现:F与IL比值为定值
概念定义:矢量-磁感应强度B=F/IL,矢量-安培力F安=ILB⊥,匀强磁场,标量-磁通φ=BS⊥
演示实验:观察通电直导线在匀强磁场中受安培力的方向(图1.1-1)
方向表示:左手伸开,四指-电流,大拇指-受力,掌心-磁感线穿入-左手定则
演示实验:观察电子束在磁场中的偏转-运动电荷在磁场中受洛伦兹力方向(图1.2-1)
方向表示:左手伸开,掌心磁感线穿入,四指-电流(+相同,-相反),大拇指-受力-左手定则
模型分析:在电流微观模型中由安培力推导洛伦兹力 ILB=NqvB F安=NF洛 F洛=qvB
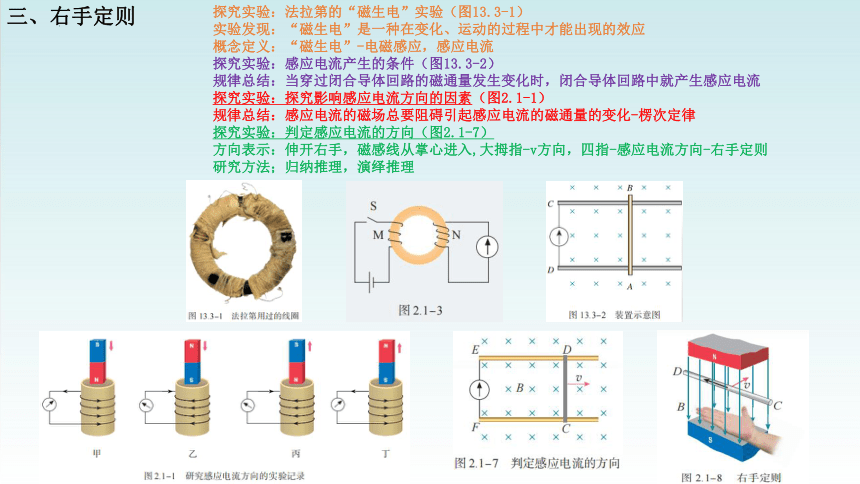
三、右手定则
探究实验:法拉第的“磁生电”实验(图13.3-1)
实验发现:“磁生电”是一种在变化、运动的过程中才能出现的效应
概念定义:“磁生电”-电磁感应,感应电流
探究实验:感应电流产生的条件(图13.3-2)
规律总结:当穿过闭合导体回路的磁通量发生变化时,闭合导体回路中就产生感应电流
探究实验:探究影响感应电流方向的因素(图2.1-1)
规律总结:感应电流的磁场总要阻碍引起感应电流的磁通量的变化-楞次定律
探究实验:判定感应电流的方向(图2.1-7)
方向表示:伸开右手,磁感线从掌心进入,大拇指-v方向,四指-感应电流方向-右手定则
研究方法;归纳推理,演绎推理
法拉第电磁感应定律
TWO
问题:
穿过闭合导体回路的磁通量发生变化,闭合导体回路中就有感应电流。感应电流的大小跟哪些因素有关呢?
实验现象:
1.在用导线切割磁感线产生感应电流的实验中,导线切割磁感线的速度越快、磁体的磁场越强,产生的感应电流就越大。
2.在向线圈中插入条形磁体的实验中,磁体的磁场越强、插入的速度越快,产生的感应电流就越大。
分析:
1.当回路中的电阻一定时,感应电流的大小可能与磁通量变化的快慢有关,而磁通量变化的快慢可以用磁通量的变化率表示。
2.电路中有感应电流,就一定有电动势。如果电路没有闭合,这时虽然没有感应电流,电动势依然存在。
定义:在电磁感应现象中产生的电动势叫作感应电动势。
产生感应电动势的那部分导体就相当于电源。
探究实验:
实验原理:磁体经过线圈时,磁通量发生变化,产生感应电动势,相当于电源,用电压表粗测其数值。
实验装置如图 2.2-1 所示,线圈的两端与电压表相连。
将强磁体从长玻璃管上端同一位置由静止下落,穿过线圈。
分别使线圈距离上管口 20 cm 、30 cm、40 cm 和 50 cm,记录电压表的示数以及发生的现象。
分别改变线圈的匝数、磁体的磁感应强度,重复上面的实验,得出定性的结论。
控制变量:
线圈越低,磁体穿过线圈时的速度就越大,磁通量的变化越快。
线圈匝数越多,感应磁场叠加变强,相当于多个电源串联。
磁体的磁感应强度越大,磁体穿过线圈磁通量变化量增多,变化更快。
法拉第电磁感应定律
德国物理学家纽曼、韦伯在对理论和实验资料进行严格分析后,于 1845 年和 1846 年先后指出:闭合电路中感应电动势的大小,跟穿过这一电路的磁通量的变化率成正比。因法拉第对电磁感应现象研究的巨大贡献,后人称之为法拉第电磁感应定律。(Faraday’s law of electromagnetic induction)
研究对象:闭合回路
导线切割磁感线时的感应电动势
如图 2.2-2 所示,把矩形线框 CDMN 放在磁感应强度
为B的匀强磁场里,线框平面跟磁感线垂直。设线框可动部分导体棒 MN 的长度为l,它以速度v向右运动,在Δt时间内,由原来的位置MN移到M1N1。
这个过程中线框的面积变化量是
穿过闭合电路的磁通量的变化量则是
根据法拉第电磁感应定律
由此求得感应电动势
E=Blv⊥
在国际单位制中,磁感应强度 B、导线长度 l、速度 v
的单位分别是特斯拉(T)、米(m)、米每秒(m/s),E 的单位是伏(V)。
研究对象:磁场中运动的一段导体
如果导线的运动方向与导线方向本身是垂直的,但与磁感线方向有一个夹角 θ(图 2.2-3),速度 v 可以分解为两个分量:
垂直于磁感线的分量 v1 = vsinθ
平行于磁感线的分量 v2 = vcosθ。
后者不切割磁感线,不产生感应电动势。
前者切割磁感线,产生的感应电动势为
一般情况下的感应电动势计算:
E=Blv
最终代入计算的有效部分是B、l、v三者相互垂直的部分。
思考与讨论
如图 2.2-4,导体棒 CD 在匀强磁场中运动。自由电荷会随着导体棒运动,并因此受到洛伦兹力。导体棒中自由电荷相对于纸面的运动大致沿什么方向?为了方便,可以认为导体棒中的自由电荷是正电荷。导体棒一直运动下去,自由电荷是否总会沿着导体棒运动?为什么?导体棒哪端的电势比较高?
以上讨论不必考虑自由电荷的热运动。
导线方向,即感应电流方向,感应电动势的方向,电源内部电流从负到正,正极电势高。
不是闭合回路,无感应电流,也有感应电动势,可用右手定则判断方向,也可通过E=Blv⊥计算大小。
电路闭合,电源两极的电荷会在外电路消耗,需要补充,会在电源内部不断的搬运正电荷到正极;
只有一根导体棒切割磁感线时,无外电路,没有电荷的消耗,所以不需要源源不断的补充电荷,电势差稳定后,自由电荷不再沿导体棒运动。
探究:感应电流的安培力
一段导线在做切割磁感线的运动时相当于一个电源,通
过上面的分析可以看到,这时的非静电力与洛伦兹力有关。
动力学特征:
在图 2.2-2 中,由于导体棒运动产生感应电动势,电路中
有电流通过,导体棒在运动过程中会受到安培力的作用。
可以判断,安培力的方向与推动导体棒运动的力的方向是
相反的。推力是动力,安培力是阻力。
做功与能量特征:
即使导体棒做匀速运动,合外力做功为零,推力也做功。
此时推力做正功,安培力做负功。
如果没有推力的作用,导体棒将克服安培力做功而消耗本身的
机械能。
F推
F安
课后题讲解
THREE
1. 有一个1 000匝的线圈,在0.4 s内通过它的磁通量从0.02 Wb增加到0.09 Wb,求线圈中的感应电动势。如果线圈的电阻是10 Ω,把一个电阻为990 Ω的电热器连接在它的两端,通过电热器的电流是多大?
解析:
先计算感应电动势,作为闭合回路的电源电动势。
再通过闭合回路欧姆定律计算干路电流。
2. 当航天飞机在环绕地球的轨道上飞行时,从中释放一颗卫星,卫星与航天飞机速度相同,两者用导电缆绳相连。这种卫星称为绳系卫星,利用它可以进行多种科学实验。现有一绳系卫星在地球赤道上空沿东西方向运行。卫星位于航天飞机的正上方,它与航天飞机之间的距离是20.5 km,卫星所在位置的地磁场B=4.6×10-5T,沿水平方向由南向北。如果航天飞机和卫星的运行速度都是7.6 km/s,求缆绳中的感应电动势。
解析:
导电缆绳,飞机与卫星连线方向,长l=20.5 km,需换算
地磁场,南北方向,B=4.6×10-5T
缆绳速度v=7.6 km/s,需换算
再代入E=Blv计算
3. 动圈式扬声器的结构如图2.2-5所示。线圈圆筒安放在永磁体磁极间的空隙中,能够在空隙中左右运动。音频电流通进线圈,安培力使线圈左右运动。纸盆与线圈连接,随着线圈振动而发声。这样的扬声器能不能当作话筒使用?也就是说,如果我们对着纸盆说话,扬声器能不能把声音变成相应的电流?为什么?
解析:
可以当作话筒,我们对着纸盆说话,声音使纸盆振动,线圈随着纸盆振动,切割磁感线产生感应电流。
扬声器:
电信号→声信号
通电导线在磁场中受力震动发声。
话筒:
声信号→电信号
闭合回路的部分导线切割磁感线产生感应电流。
4. 如图2.2-6,矩形线圈在匀强磁场中绕OO′轴匀速转动时,线圈中的感应电动势是否变化?为什么?设线圈的两个边长分别是l1和l2,转动时角速度是ω,磁场的磁感应强度为B。试证明:
在图示位置时,线圈中的感应电动势为E=BSω,式中S=l1l2,为线圈面积。
解析:图示位置,只有转轴对边的导线l2在切割磁感线,速度为圆周运动线速度。
E=Bl2v=Bl2ωl1=BSω
闭合回路的磁通量发生变化时也可用导线切割磁感线产生的感应电动势公式。
5. 图2.2-7是电磁流量计的示意图。圆管由非磁性材料制成,空间有匀强磁场。当管中的导电液体流过磁场区域时,测出管壁上M、N两点间的电势差U,就可以知道管中液体的流量
Q—单位时间内流过管道横截面的液体体积。已知管的直径为d,磁感应强度为B,试推出Q与U关系的表达式。假定管中各处液体的流速相同。电磁流量计的管道内没有任何阻碍液体流动的结构,所以常用来测量高黏度及强腐蚀性流体的流量。它的优点是测量范围宽、反应快、易与其他自动控制装置配套。
解析:
管内有导电液体流过时,等效为一段长为d的导体在切割磁感线。
U=E=Bdv。液体的流量Q=vπ(d/2)2
二式联立,消去v,即可。
6. 一长为l的导体棒在磁感应强度为B的匀强磁场中绕其一端以角速度ω在垂直于磁场的平面内匀速转动(图2.2-8),求ab两端产生的感应电动势。
解析:
方法一总结:
虽然此时没有闭合回路,也没有磁通量,但是可以将导体棒扫过的面积转化为面积变化量计算磁通量变化。
两种产生感应电动势方式的本质是一样的。
方法二总结:
各个位置的线速度大小不同,但是方向都垂直与导体棒,将其看成一段段小导线切割磁感线,产生的感应电动势方向也是一致的,可看成串联。
找导线上对称的两段进行研究,
每段产生E=BΔlvr=BΔlwr
两段产生
E合=BΔl(v1+v2)=BΔl(v1+v2)=BΔl2v中=BΔlv
=BΔlw(r1+r2)=BΔlwl 两段等效为一段
导体各位置相加E总=B(l/2)v
=B(l/2)wl=Bl2w
7. 如图,有两个同心导体圆环,内环中通有顺时针方向的电流,外环中原来无电流.当内环中电流逐渐增大时,
外环中感应电流的方向为___.(填顺时针或者逆时针)
外环的运动趋势是___(填收缩或者扩张)
1.用右手螺旋定则判定小圆环内外磁场方向。
大圆环内有所有的叉磁场和部分点磁场。
2.电流增大,点磁场和叉磁场同时增大,磁感线闭合,空间总增加量相同。大圆环内叉磁场增加量大于点磁场增加量,表现为叉磁场增强。
3.通过增反减同,判断出感生磁场为点,电流方向是逆时针。
4.通过左手定则判断大圆环受力,呈扩张趋势。
注意:判断受力不能用“增反”
增反-处于叉磁场中,且叉磁场增强,
本题-大圆环处于点磁场中,叉磁场增强。
8. 如图1所示,闭合线圈abcd在磁场中运动到如图所示位置时,ab边受到的磁场力竖直向上,此线圈的运动情况可能是 ( B )
A.向右进入磁场
B.向左移出磁场
C.以ab为轴转动
D.以cd为轴转动
解析:
由题可知,感应电流由a到b,在线框中沿顺时针方向,感生磁场为叉磁场,愿磁场方向为叉,可知由磁通量减小产生。故AB中B对。
线框随ab轴或cd轴转动时,只有转轴对边有可能切割磁感线,当线框在图示位置时,该边的瞬时速度即圆周运动的线速度,方向与磁场平行,不切割磁感线。
该位置也被定义为交变电流发电机的中性面,有最大的磁通量,无感应电动势。
F
a
b
c
d
谢谢观看
作业:完成2.2节金榜、课时作业
2.2电磁感应定律
用左右手确定方向的电磁学定则
01
法拉第电磁感应定律
02
课后题讲解
03
目录
用左右手确定方向的电磁学定则
ONE
一、右手螺旋定则
探究实验:奥斯特的小磁针实验
实验发现:电流的磁效应
演示实验:用细铁屑表示通电直导线磁场分布
方向表示:将右手螺旋状来描述通电导线的磁场和电流方向-右手螺旋定则
二、左手定则
理论基础:通电导线(磁体)与其他磁体有力的作用
探究实验:匀强磁场中探究通电导线受力的因素(图13.2-1)
实验发现:F与IL比值为定值
概念定义:矢量-磁感应强度B=F/IL,矢量-安培力F安=ILB⊥,匀强磁场,标量-磁通φ=BS⊥
演示实验:观察通电直导线在匀强磁场中受安培力的方向(图1.1-1)
方向表示:左手伸开,四指-电流,大拇指-受力,掌心-磁感线穿入-左手定则
演示实验:观察电子束在磁场中的偏转-运动电荷在磁场中受洛伦兹力方向(图1.2-1)
方向表示:左手伸开,掌心磁感线穿入,四指-电流(+相同,-相反),大拇指-受力-左手定则
模型分析:在电流微观模型中由安培力推导洛伦兹力 ILB=NqvB F安=NF洛 F洛=qvB
三、右手定则
探究实验:法拉第的“磁生电”实验(图13.3-1)
实验发现:“磁生电”是一种在变化、运动的过程中才能出现的效应
概念定义:“磁生电”-电磁感应,感应电流
探究实验:感应电流产生的条件(图13.3-2)
规律总结:当穿过闭合导体回路的磁通量发生变化时,闭合导体回路中就产生感应电流
探究实验:探究影响感应电流方向的因素(图2.1-1)
规律总结:感应电流的磁场总要阻碍引起感应电流的磁通量的变化-楞次定律
探究实验:判定感应电流的方向(图2.1-7)
方向表示:伸开右手,磁感线从掌心进入,大拇指-v方向,四指-感应电流方向-右手定则
研究方法;归纳推理,演绎推理
法拉第电磁感应定律
TWO
问题:
穿过闭合导体回路的磁通量发生变化,闭合导体回路中就有感应电流。感应电流的大小跟哪些因素有关呢?
实验现象:
1.在用导线切割磁感线产生感应电流的实验中,导线切割磁感线的速度越快、磁体的磁场越强,产生的感应电流就越大。
2.在向线圈中插入条形磁体的实验中,磁体的磁场越强、插入的速度越快,产生的感应电流就越大。
分析:
1.当回路中的电阻一定时,感应电流的大小可能与磁通量变化的快慢有关,而磁通量变化的快慢可以用磁通量的变化率表示。
2.电路中有感应电流,就一定有电动势。如果电路没有闭合,这时虽然没有感应电流,电动势依然存在。
定义:在电磁感应现象中产生的电动势叫作感应电动势。
产生感应电动势的那部分导体就相当于电源。
探究实验:
实验原理:磁体经过线圈时,磁通量发生变化,产生感应电动势,相当于电源,用电压表粗测其数值。
实验装置如图 2.2-1 所示,线圈的两端与电压表相连。
将强磁体从长玻璃管上端同一位置由静止下落,穿过线圈。
分别使线圈距离上管口 20 cm 、30 cm、40 cm 和 50 cm,记录电压表的示数以及发生的现象。
分别改变线圈的匝数、磁体的磁感应强度,重复上面的实验,得出定性的结论。
控制变量:
线圈越低,磁体穿过线圈时的速度就越大,磁通量的变化越快。
线圈匝数越多,感应磁场叠加变强,相当于多个电源串联。
磁体的磁感应强度越大,磁体穿过线圈磁通量变化量增多,变化更快。
法拉第电磁感应定律
德国物理学家纽曼、韦伯在对理论和实验资料进行严格分析后,于 1845 年和 1846 年先后指出:闭合电路中感应电动势的大小,跟穿过这一电路的磁通量的变化率成正比。因法拉第对电磁感应现象研究的巨大贡献,后人称之为法拉第电磁感应定律。(Faraday’s law of electromagnetic induction)
研究对象:闭合回路
导线切割磁感线时的感应电动势
如图 2.2-2 所示,把矩形线框 CDMN 放在磁感应强度
为B的匀强磁场里,线框平面跟磁感线垂直。设线框可动部分导体棒 MN 的长度为l,它以速度v向右运动,在Δt时间内,由原来的位置MN移到M1N1。
这个过程中线框的面积变化量是
穿过闭合电路的磁通量的变化量则是
根据法拉第电磁感应定律
由此求得感应电动势
E=Blv⊥
在国际单位制中,磁感应强度 B、导线长度 l、速度 v
的单位分别是特斯拉(T)、米(m)、米每秒(m/s),E 的单位是伏(V)。
研究对象:磁场中运动的一段导体
如果导线的运动方向与导线方向本身是垂直的,但与磁感线方向有一个夹角 θ(图 2.2-3),速度 v 可以分解为两个分量:
垂直于磁感线的分量 v1 = vsinθ
平行于磁感线的分量 v2 = vcosθ。
后者不切割磁感线,不产生感应电动势。
前者切割磁感线,产生的感应电动势为
一般情况下的感应电动势计算:
E=Blv
最终代入计算的有效部分是B、l、v三者相互垂直的部分。
思考与讨论
如图 2.2-4,导体棒 CD 在匀强磁场中运动。自由电荷会随着导体棒运动,并因此受到洛伦兹力。导体棒中自由电荷相对于纸面的运动大致沿什么方向?为了方便,可以认为导体棒中的自由电荷是正电荷。导体棒一直运动下去,自由电荷是否总会沿着导体棒运动?为什么?导体棒哪端的电势比较高?
以上讨论不必考虑自由电荷的热运动。
导线方向,即感应电流方向,感应电动势的方向,电源内部电流从负到正,正极电势高。
不是闭合回路,无感应电流,也有感应电动势,可用右手定则判断方向,也可通过E=Blv⊥计算大小。
电路闭合,电源两极的电荷会在外电路消耗,需要补充,会在电源内部不断的搬运正电荷到正极;
只有一根导体棒切割磁感线时,无外电路,没有电荷的消耗,所以不需要源源不断的补充电荷,电势差稳定后,自由电荷不再沿导体棒运动。
探究:感应电流的安培力
一段导线在做切割磁感线的运动时相当于一个电源,通
过上面的分析可以看到,这时的非静电力与洛伦兹力有关。
动力学特征:
在图 2.2-2 中,由于导体棒运动产生感应电动势,电路中
有电流通过,导体棒在运动过程中会受到安培力的作用。
可以判断,安培力的方向与推动导体棒运动的力的方向是
相反的。推力是动力,安培力是阻力。
做功与能量特征:
即使导体棒做匀速运动,合外力做功为零,推力也做功。
此时推力做正功,安培力做负功。
如果没有推力的作用,导体棒将克服安培力做功而消耗本身的
机械能。
F推
F安
课后题讲解
THREE
1. 有一个1 000匝的线圈,在0.4 s内通过它的磁通量从0.02 Wb增加到0.09 Wb,求线圈中的感应电动势。如果线圈的电阻是10 Ω,把一个电阻为990 Ω的电热器连接在它的两端,通过电热器的电流是多大?
解析:
先计算感应电动势,作为闭合回路的电源电动势。
再通过闭合回路欧姆定律计算干路电流。
2. 当航天飞机在环绕地球的轨道上飞行时,从中释放一颗卫星,卫星与航天飞机速度相同,两者用导电缆绳相连。这种卫星称为绳系卫星,利用它可以进行多种科学实验。现有一绳系卫星在地球赤道上空沿东西方向运行。卫星位于航天飞机的正上方,它与航天飞机之间的距离是20.5 km,卫星所在位置的地磁场B=4.6×10-5T,沿水平方向由南向北。如果航天飞机和卫星的运行速度都是7.6 km/s,求缆绳中的感应电动势。
解析:
导电缆绳,飞机与卫星连线方向,长l=20.5 km,需换算
地磁场,南北方向,B=4.6×10-5T
缆绳速度v=7.6 km/s,需换算
再代入E=Blv计算
3. 动圈式扬声器的结构如图2.2-5所示。线圈圆筒安放在永磁体磁极间的空隙中,能够在空隙中左右运动。音频电流通进线圈,安培力使线圈左右运动。纸盆与线圈连接,随着线圈振动而发声。这样的扬声器能不能当作话筒使用?也就是说,如果我们对着纸盆说话,扬声器能不能把声音变成相应的电流?为什么?
解析:
可以当作话筒,我们对着纸盆说话,声音使纸盆振动,线圈随着纸盆振动,切割磁感线产生感应电流。
扬声器:
电信号→声信号
通电导线在磁场中受力震动发声。
话筒:
声信号→电信号
闭合回路的部分导线切割磁感线产生感应电流。
4. 如图2.2-6,矩形线圈在匀强磁场中绕OO′轴匀速转动时,线圈中的感应电动势是否变化?为什么?设线圈的两个边长分别是l1和l2,转动时角速度是ω,磁场的磁感应强度为B。试证明:
在图示位置时,线圈中的感应电动势为E=BSω,式中S=l1l2,为线圈面积。
解析:图示位置,只有转轴对边的导线l2在切割磁感线,速度为圆周运动线速度。
E=Bl2v=Bl2ωl1=BSω
闭合回路的磁通量发生变化时也可用导线切割磁感线产生的感应电动势公式。
5. 图2.2-7是电磁流量计的示意图。圆管由非磁性材料制成,空间有匀强磁场。当管中的导电液体流过磁场区域时,测出管壁上M、N两点间的电势差U,就可以知道管中液体的流量
Q—单位时间内流过管道横截面的液体体积。已知管的直径为d,磁感应强度为B,试推出Q与U关系的表达式。假定管中各处液体的流速相同。电磁流量计的管道内没有任何阻碍液体流动的结构,所以常用来测量高黏度及强腐蚀性流体的流量。它的优点是测量范围宽、反应快、易与其他自动控制装置配套。
解析:
管内有导电液体流过时,等效为一段长为d的导体在切割磁感线。
U=E=Bdv。液体的流量Q=vπ(d/2)2
二式联立,消去v,即可。
6. 一长为l的导体棒在磁感应强度为B的匀强磁场中绕其一端以角速度ω在垂直于磁场的平面内匀速转动(图2.2-8),求ab两端产生的感应电动势。
解析:
方法一总结:
虽然此时没有闭合回路,也没有磁通量,但是可以将导体棒扫过的面积转化为面积变化量计算磁通量变化。
两种产生感应电动势方式的本质是一样的。
方法二总结:
各个位置的线速度大小不同,但是方向都垂直与导体棒,将其看成一段段小导线切割磁感线,产生的感应电动势方向也是一致的,可看成串联。
找导线上对称的两段进行研究,
每段产生E=BΔlvr=BΔlwr
两段产生
E合=BΔl(v1+v2)=BΔl(v1+v2)=BΔl2v中=BΔlv
=BΔlw(r1+r2)=BΔlwl 两段等效为一段
导体各位置相加E总=B(l/2)v
=B(l/2)wl=Bl2w
7. 如图,有两个同心导体圆环,内环中通有顺时针方向的电流,外环中原来无电流.当内环中电流逐渐增大时,
外环中感应电流的方向为___.(填顺时针或者逆时针)
外环的运动趋势是___(填收缩或者扩张)
1.用右手螺旋定则判定小圆环内外磁场方向。
大圆环内有所有的叉磁场和部分点磁场。
2.电流增大,点磁场和叉磁场同时增大,磁感线闭合,空间总增加量相同。大圆环内叉磁场增加量大于点磁场增加量,表现为叉磁场增强。
3.通过增反减同,判断出感生磁场为点,电流方向是逆时针。
4.通过左手定则判断大圆环受力,呈扩张趋势。
注意:判断受力不能用“增反”
增反-处于叉磁场中,且叉磁场增强,
本题-大圆环处于点磁场中,叉磁场增强。
8. 如图1所示,闭合线圈abcd在磁场中运动到如图所示位置时,ab边受到的磁场力竖直向上,此线圈的运动情况可能是 ( B )
A.向右进入磁场
B.向左移出磁场
C.以ab为轴转动
D.以cd为轴转动
解析:
由题可知,感应电流由a到b,在线框中沿顺时针方向,感生磁场为叉磁场,愿磁场方向为叉,可知由磁通量减小产生。故AB中B对。
线框随ab轴或cd轴转动时,只有转轴对边有可能切割磁感线,当线框在图示位置时,该边的瞬时速度即圆周运动的线速度,方向与磁场平行,不切割磁感线。
该位置也被定义为交变电流发电机的中性面,有最大的磁通量,无感应电动势。
F
a
b
c
d
谢谢观看
作业:完成2.2节金榜、课时作业
