24.2.2直线与圆的位置关系(切线的判定定理)[上学期]
文档属性
| 名称 | 24.2.2直线与圆的位置关系(切线的判定定理)[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 67.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-11-01 22:23:00 | ||
图片预览





文档简介
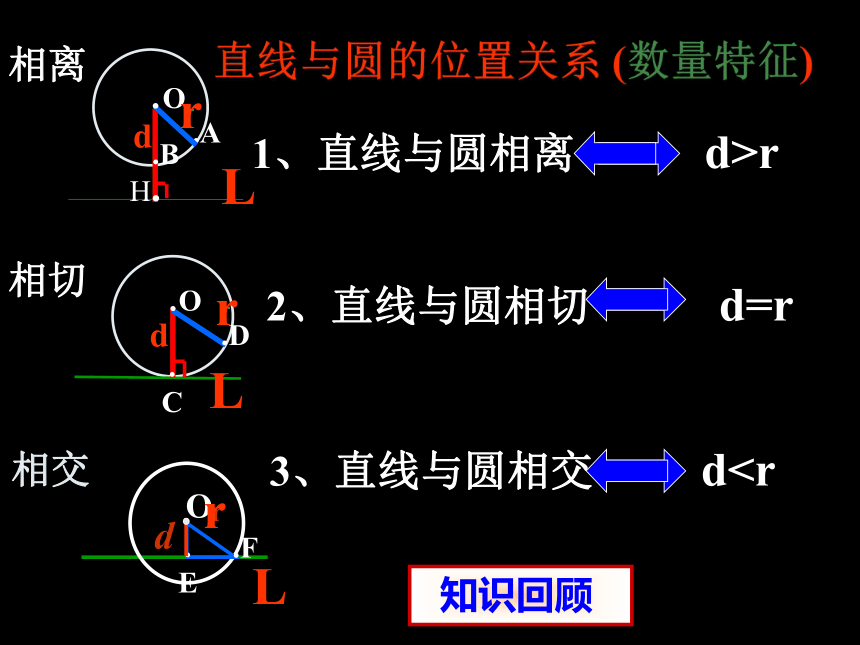
课件14张PPT。24.2.2直线与圆的位置关系dr相离.Adr相切LLH.直线与圆的位置关系 (数量特征).D.Ord相交.
C.O.B.
E.FOLrrr观察与发现
图中直线l是⊙O的切线,怎样判定?答:①直线与圆有唯一公共点;
②直线到圆心的距离等于该圆的半径;
思考判定一条直线是不是圆的切线除了这两种方法外还有其它方法吗?问题1 如图,已知⊙O上一点A ,怎样根据圆的切线的定义过A作⊙O的切线?发现:(1)直线l经过半径OA的外端点A;(2)直线l垂直于半径OA.问题2 观察你所作出的切线,对圆的半径
OA来说,这条切线应具有哪两个特征?问题3 如果一条直线符合了上面两个特征,这条直线是不是圆的切线?OAl作法: 1)连结OA.
2)过点A 作OA的垂线l请你用语言概括所得的结论(二)切线的判定定理:
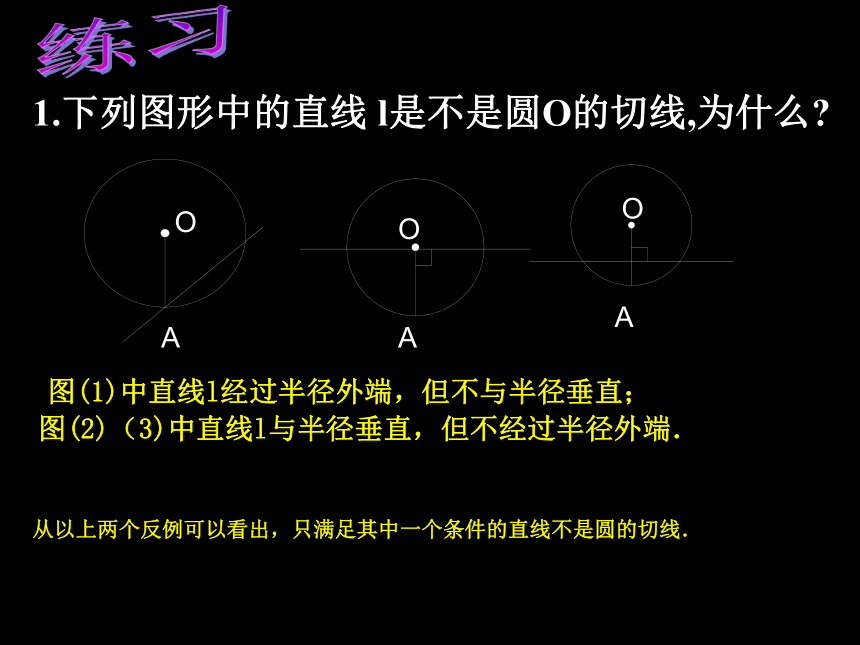
1、切线的判定定理:经过半径外端并且垂直于这条半径的直线是圆的切线.2、对定理的理解:切线需满足两条: ①经过半径外端.②垂直于这条半径. 注意:定理中的两个条件缺一不可. 图(1)中直线l经过半径外端,但不与半径垂直;
图(2)(3)中直线l与半径垂直,但不经过半径外端.
1.下列图形中的直线 l是不是圆O的切线,为什么?练习从以上两个反例可以看出,只满足其中一个条件的直线不是圆的切线.
2.判断下列命题是否正确.
(1)经过半径外端的直线是圆的切线.( )
(2)垂直于半径的直线是圆的切线.( )
(3)过直径的外端并且垂直于这条直径的直线是圆 的切线.( )
(4)和圆有一个公共点的直线是圆的切线.( )
(5)以等腰三角形的顶点为圆心,底边上的高为半径的圆与底边相切.( )
××√√
√
(三)切线的判定方法有三种:①直线与圆有唯一公共点;②直线到圆心的距离等于该圆的半径;③切线的判定定理.(四)应用定理.
例1 已知:直线AB经过⊙O上的点C,
并且OA=OB,CA=CB.
求证:直线AB是⊙O的切线. 直线AB经过半径0C的外端C,并且垂直于半径0C, 所以AB是⊙O的切线. ABCO证明:连结0C∵0A=0B,CA=CB,∴0C是等腰三角形0AB底边AB上的中线.∴AB⊥OC.方法小结: 证明过圆上一点的直线是圆的切线.只要证明这条直线垂直于经过切点的半径.例2.如图,线段AB经过圆心O,交⊙O于点A,C,∠BAD=∠B=30°,边BD交圆于点D。
求证:BD是⊙O的切线证明:连结OD∵ OA=OD , ∴ OD⊥BD又∵直线BD 经过⊙O上的D点∴直线BD是⊙O的切线∴∠ODA=∠A=300ABCD∴∠BDO=90°如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点的切线互相垂直,垂足为D.
求证:AC平分∠DAB.
??????????????
.
???????????????????????????
能力与拓展1.如图所示,△ABC中,AC=BC,以BC为直径的⊙O交AB于D,过点D作DE⊥AC于点E,交BC的延长线于点F.
求证:(1)AD=BD;
(2)DF是⊙O的切线.能力与拓展2.如图所示,在△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于D,E是BC的中点,连接ED并延长交BA的延长线于F.
求证:DE是⊙O的切线∟∟∟1234切线的判定定理:
经过半径外端并且垂直于这条半径的直线是圆的切线.小结:
C.O.B.
E.FOLrrr观察与发现
图中直线l是⊙O的切线,怎样判定?答:①直线与圆有唯一公共点;
②直线到圆心的距离等于该圆的半径;
思考判定一条直线是不是圆的切线除了这两种方法外还有其它方法吗?问题1 如图,已知⊙O上一点A ,怎样根据圆的切线的定义过A作⊙O的切线?发现:(1)直线l经过半径OA的外端点A;(2)直线l垂直于半径OA.问题2 观察你所作出的切线,对圆的半径
OA来说,这条切线应具有哪两个特征?问题3 如果一条直线符合了上面两个特征,这条直线是不是圆的切线?OAl作法: 1)连结OA.
2)过点A 作OA的垂线l请你用语言概括所得的结论(二)切线的判定定理:
1、切线的判定定理:经过半径外端并且垂直于这条半径的直线是圆的切线.2、对定理的理解:切线需满足两条: ①经过半径外端.②垂直于这条半径. 注意:定理中的两个条件缺一不可. 图(1)中直线l经过半径外端,但不与半径垂直;
图(2)(3)中直线l与半径垂直,但不经过半径外端.
1.下列图形中的直线 l是不是圆O的切线,为什么?练习从以上两个反例可以看出,只满足其中一个条件的直线不是圆的切线.
2.判断下列命题是否正确.
(1)经过半径外端的直线是圆的切线.( )
(2)垂直于半径的直线是圆的切线.( )
(3)过直径的外端并且垂直于这条直径的直线是圆 的切线.( )
(4)和圆有一个公共点的直线是圆的切线.( )
(5)以等腰三角形的顶点为圆心,底边上的高为半径的圆与底边相切.( )
××√√
√
(三)切线的判定方法有三种:①直线与圆有唯一公共点;②直线到圆心的距离等于该圆的半径;③切线的判定定理.(四)应用定理.
例1 已知:直线AB经过⊙O上的点C,
并且OA=OB,CA=CB.
求证:直线AB是⊙O的切线. 直线AB经过半径0C的外端C,并且垂直于半径0C, 所以AB是⊙O的切线. ABCO证明:连结0C∵0A=0B,CA=CB,∴0C是等腰三角形0AB底边AB上的中线.∴AB⊥OC.方法小结: 证明过圆上一点的直线是圆的切线.只要证明这条直线垂直于经过切点的半径.例2.如图,线段AB经过圆心O,交⊙O于点A,C,∠BAD=∠B=30°,边BD交圆于点D。
求证:BD是⊙O的切线证明:连结OD∵ OA=OD , ∴ OD⊥BD又∵直线BD 经过⊙O上的D点∴直线BD是⊙O的切线∴∠ODA=∠A=300ABCD∴∠BDO=90°如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点的切线互相垂直,垂足为D.
求证:AC平分∠DAB.
??????????????
.
???????????????????????????
能力与拓展1.如图所示,△ABC中,AC=BC,以BC为直径的⊙O交AB于D,过点D作DE⊥AC于点E,交BC的延长线于点F.
求证:(1)AD=BD;
(2)DF是⊙O的切线.能力与拓展2.如图所示,在△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于D,E是BC的中点,连接ED并延长交BA的延长线于F.
求证:DE是⊙O的切线∟∟∟1234切线的判定定理:
经过半径外端并且垂直于这条半径的直线是圆的切线.小结:
同课章节目录
