24.1.3

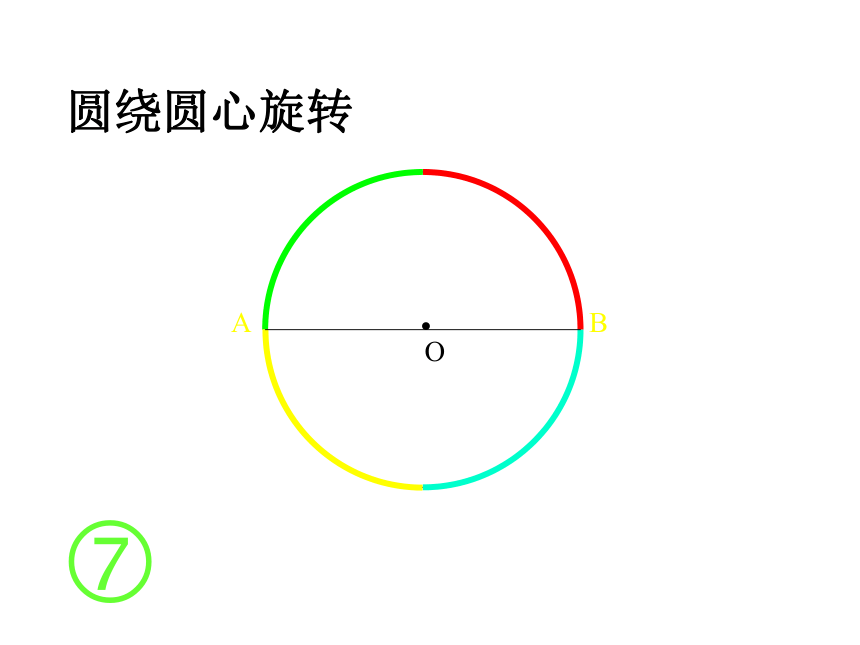
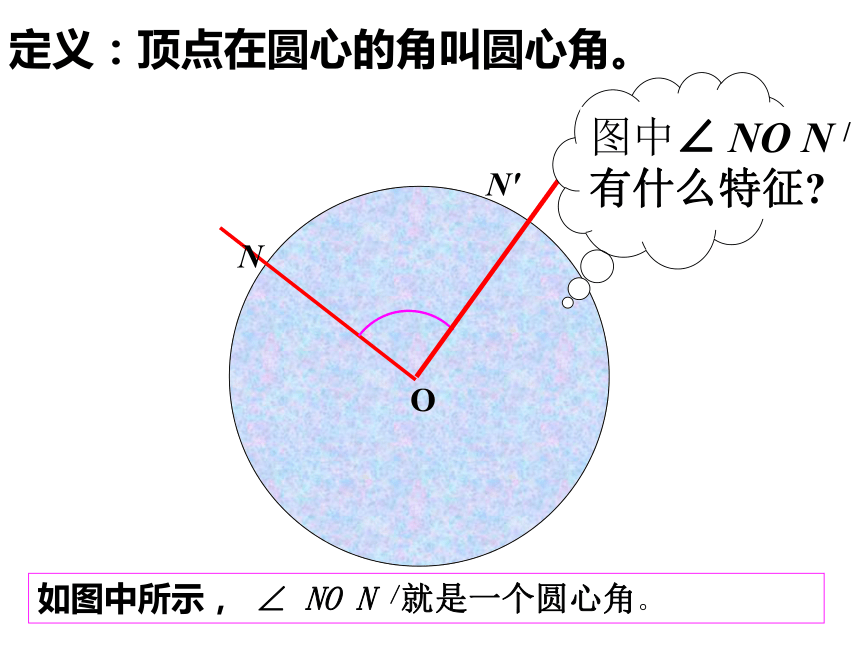
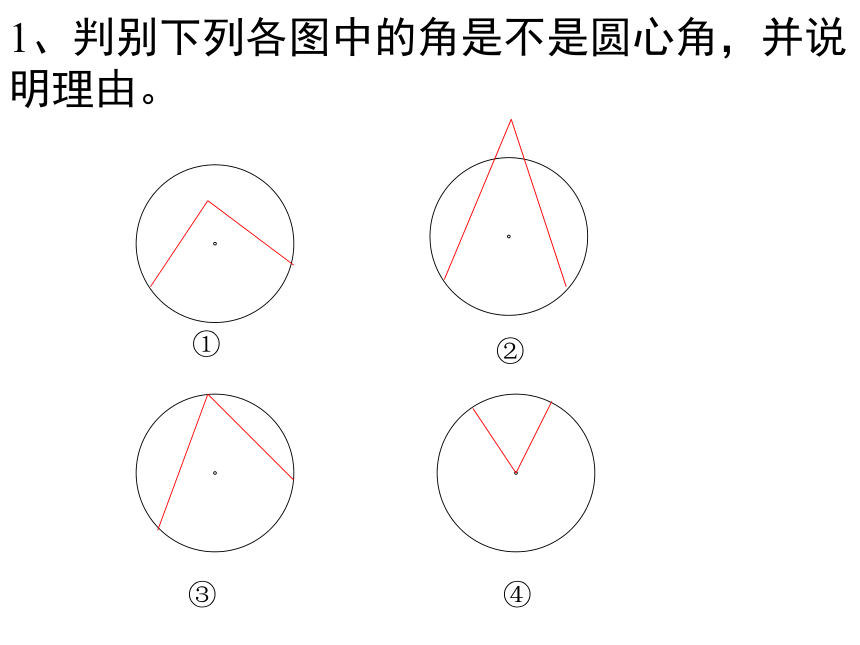
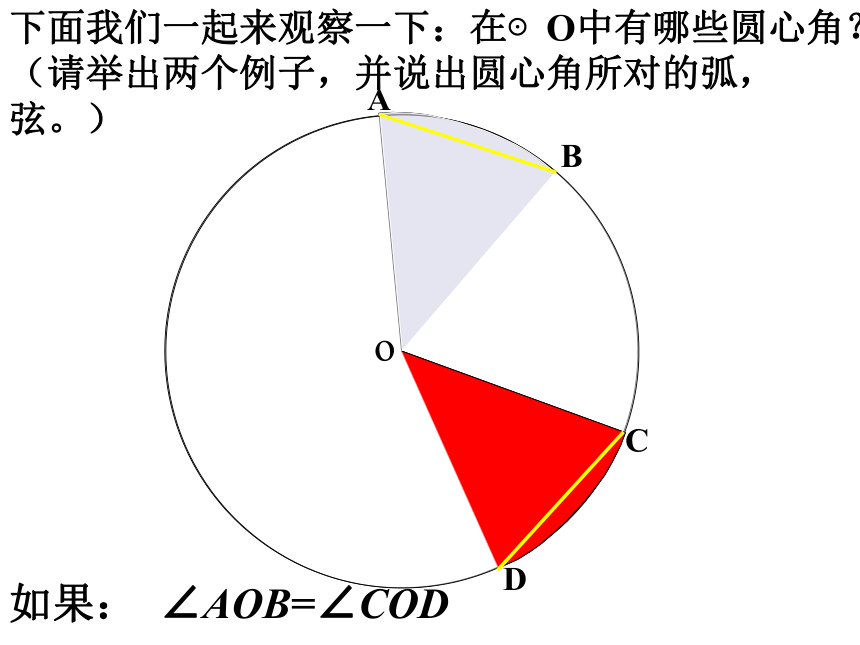
课件19张PPT。24.1.3弧.弦.圆心角AB圆绕圆心旋转?AB圆绕圆心旋转?AB?把圆绕圆心旋转任意一个角度后，仍与原来的圆重合。如图中所示， ∠ NO N /就是一个圆心角。NON'?定义：顶点在圆心的角叫圆心角。1、判别下列各图中的角是不是圆心角，并说明理由。①②③④ABCDo下面我们一起来观察一下：在⊙O中有哪些圆心角？（请举出两个例子，并说出圆心角所对的弧，弦。）如果： ∠AOB=∠COD证明:∵OA=OC ，OB=OD，
∠AOB=∠COD,
∴ 当点A与点C重合时，
点B与点D也重合。

∴　AB=CD，
已知:如图∠AOB=∠ COD,
求证: AB=CD，AB = CD。⌒⌒OAB下面的说法正确吗?为什么?
如图,因为 ，根据圆心角、弧、弦、
的关系定理可知： ⌒⌒圆心角定理：在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦也相等。　　　　　　　　　　　　　推论在同圆或等圆中,如果①两个圆心角,②两条弧,③两条弦,④两条弦心距中,有一组量相等,那么它们所对应的其余各组量都分别相等.如由条件:③AB=A′B′④ OD=O′D′①∠AOB=∠A′O′B′ 抢答题
已知：如图，AB，CD是⊙O的两条弦，
OE，OF为AB、CD的弦心距，根据这
节课所学的定理及推论填空：ABCFDEO（2）如果OE=OF，那么 ， ， ；（4）如果AB=CD，那么 ， ， 。(1)如果∠AOB=∠COD，那么 ， ， ;∠AOB=∠COD AB=CD OE=OF已知:如图,A,B,C,D是⊙O上的点，∠1=∠2。
求证：AC=BD例2:例3：已知：如图, AB、DE是⊙O的两条直径，C是⊙O上一点，且AD=CE。求证：BE=CE⌒⌒1.如图，在⊙O中，AC=BD， ，
求∠2的度数。
?
?︵︵练习2.如图，在⊙O中，AB＝AC，∠B＝70°.
求∠C度数.
3.如图，AB是直径，BC＝CD＝DE，
∠BOC＝40°，求∠AOE的度数 练习︵︵︵︵︵2.如图，在⊙O中，AB＝AC，∠B＝70°.
求∠C度数.
3.如图，AB是直径，BC＝CD＝DE，
∠BOC＝40°，求∠AOE的度数 练习︵︵︵︵︵4.如图，在⊙O中，，∠1＝ ∠2,
试说明:AC= BD
5.如图，已知AD＝BC，
试说明AB=CD练习︵︵今天你学到的什么？