11.2.2三角形的外角 课件(共25张PPT)
文档属性
| 名称 | 11.2.2三角形的外角 课件(共25张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 441.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-08 09:42:18 | ||
图片预览



文档简介
(共25张PPT)
学习目标:
1、掌握三角形的外角定义及内角之间的关系。
2、掌握三角形的外角性质,能对定理进行推理论证。
3、能运用三角形的内角、外角性质定理进行解答或证明有关几何问题。
一、阅读课本P14-15, 回答下列问题
1、三角形的外角的定义是什么?
2、三角形的外角等于 。
3、三角形的外角大于 。
4、三角形的外角和等于 度
5、完成课本第15-16页练习
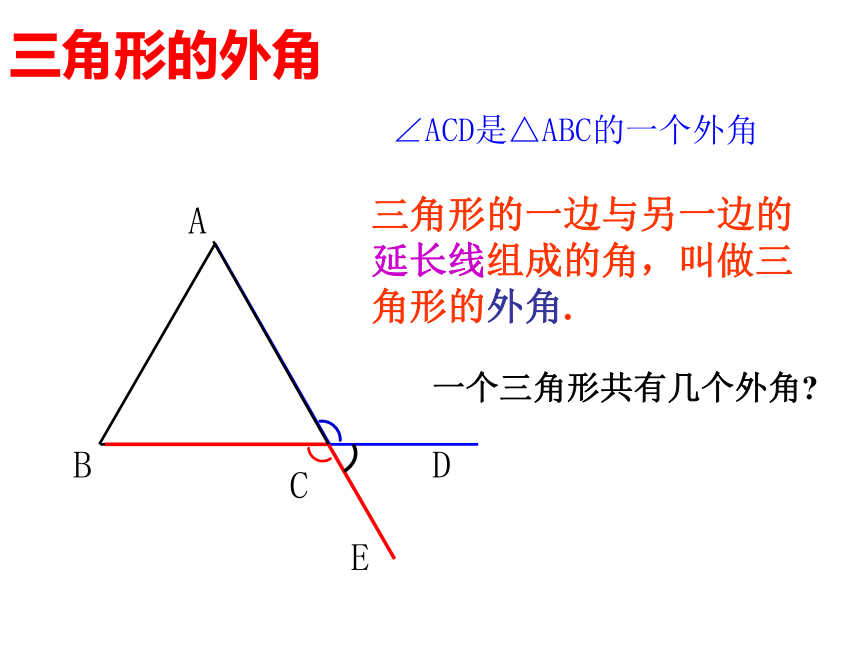
三角形的外角
A
B
C
D
∠ACD是△ABC的一个外角
三角形的一边与另一边的延长线组成的角,叫做三角形的外角.
E
一个三角形共有几个外角
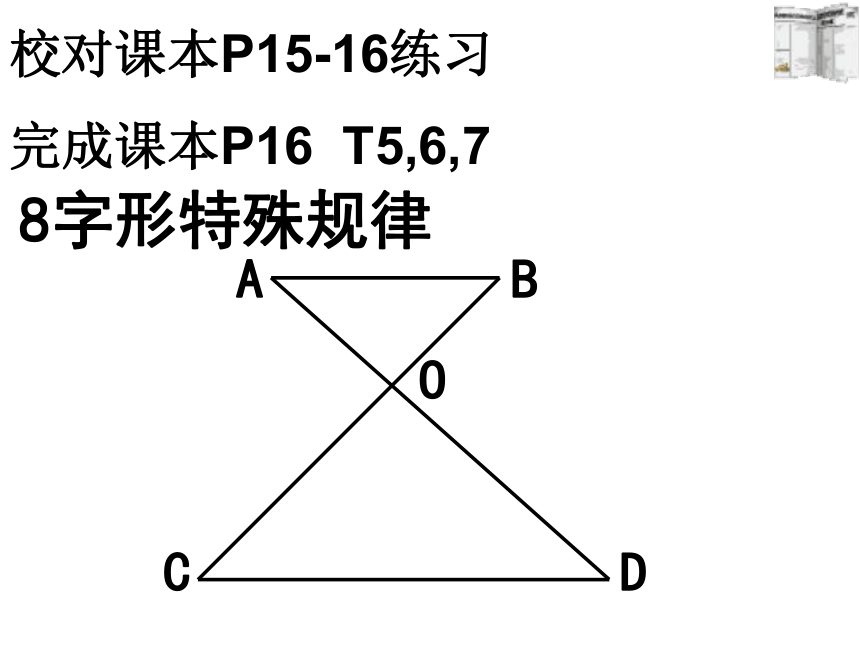
校对课本P15-16练习
完成课本P16 T5,6,7
8字形特殊规律
A
B
C
D
O
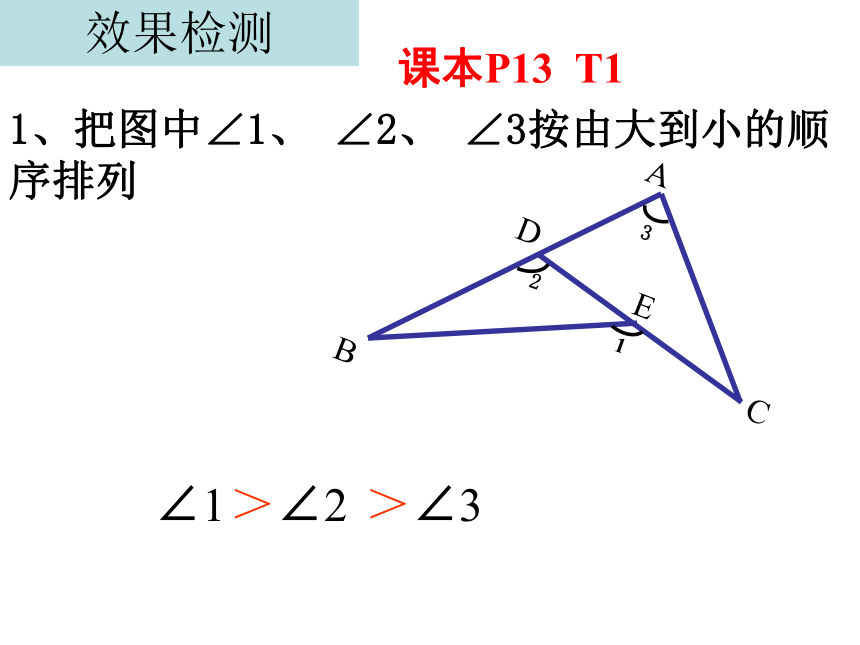
1、把图中∠1、 ∠2、 ∠3按由大到小的顺序排列
B
3
2
1
A
C
D
E
∠1
∠2
∠3
>
>
效果检测
课本P13 T1
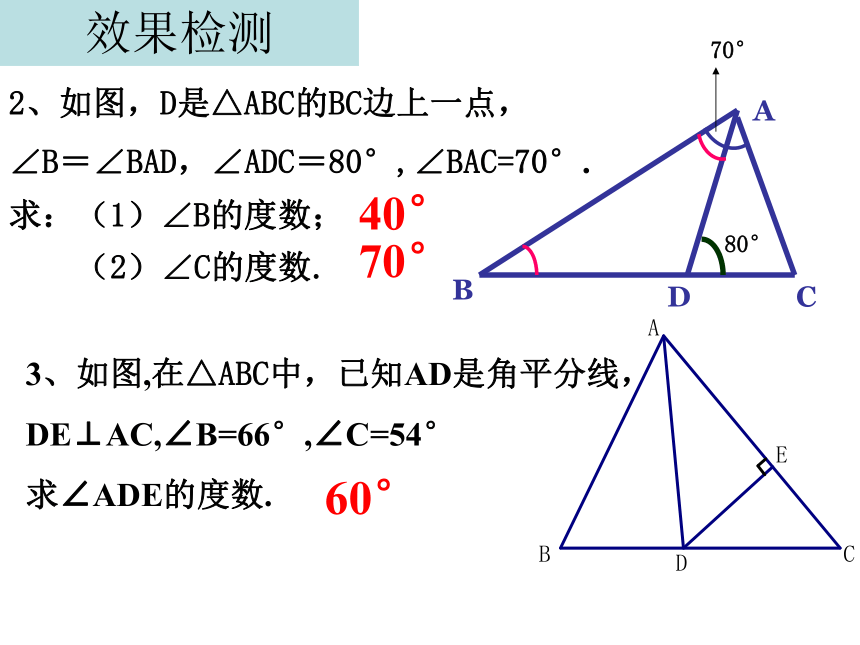
2、如图,D是△ABC的BC边上一点,
∠B=∠BAD,∠ADC=80°,∠BAC=70°.
求:(1)∠B的度数;
(2)∠C的度数.
A
B
C
D
80°
70°
3、如图,在△ABC中,已知AD是角平分线,
DE⊥AC,∠B=66°,∠C=54°
求∠ADE的度数.
效果检测
40°
70°
60°
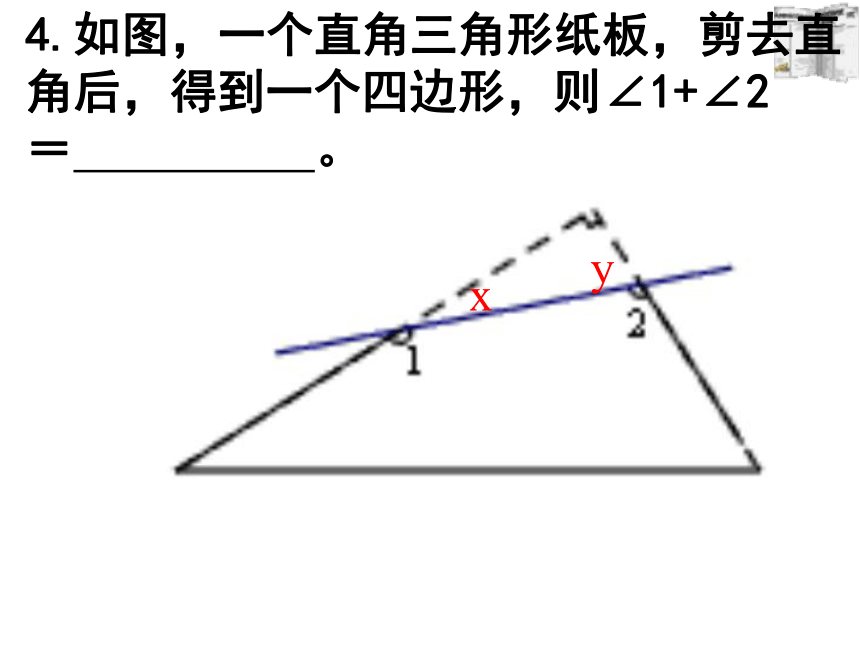
4.如图,一个直角三角形纸板,剪去直角后,得到一个四边形,则∠1+∠2= 。
x
y
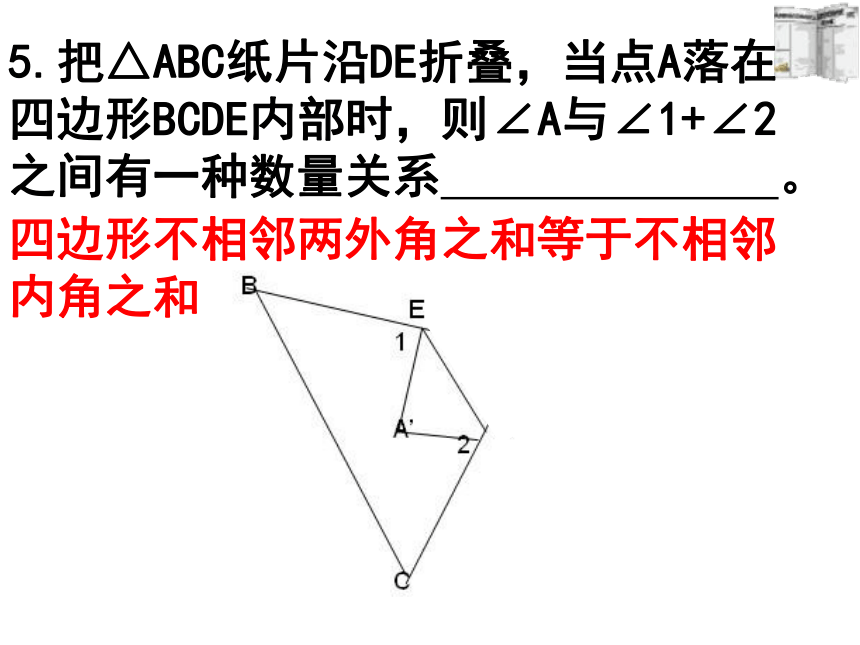
5.把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则∠A与∠1+∠2之间有一种数量关系 。
四边形不相邻两外角之和等于不相邻内角之和
6.在五角星中,
∠A+∠B+∠C+∠D+∠E= .
小亮从A点出发,沿直线前进10米后
最终回到了A点,他共走了 米。
7.某零件如图所示,图纸要求∠A=90°,
∠B=32°,∠BDC=145°∠C= .
∠B、∠C、∠BDC 、∠A三角之间有何关系
E
8.如图是一副三角尺拼成的图案,则∠AEB= .
效果测试
9.如图,求∠A+∠B+∠C+∠D+∠E的度数.(至少两种方法)
F
10.如图,求:∠A+∠B+∠C+
∠D+∠E+∠F= .
11.一副三角板有两个直角三角形,如图叠放在一起,则∠α的度数是= .
12.如图2,∠1+∠2+∠3+∠ 4的值为 .
13.如图,求:∠A+∠B+∠C+∠D+∠E+∠F= .
14.如图,求∠A +∠B +∠C +∠D+∠E +∠F的度数
特殊图形中角的转化问题
截角五角星
15.如图,则∠A+∠B+∠C+∠D+∠E+∠F=______.
16.(1)如图(1),在△ABC中,∠A=α,∠ABC的平分线与
∠ACD的平分线交于点A1得∠A1,求∠A1的度数。
(2)如图(2),∠A1BC的平分线与∠A1CD的平分线交于
点A2,得∠A2 ,…, 则∠An= .
17. 则∠A、∠B、∠C与∠BDC之间有一种数量关系 。
凹角等于不相邻它的三个内角之和
17. 则AP,CP为角平分线,则∠D、∠B、与∠P之间有一种数量关系 。
8字形,两上角之和等于两下角之和
2、《全品》P9-10
课后作业
学习目标:
1、掌握三角形的外角定义及内角之间的关系。
2、掌握三角形的外角性质,能对定理进行推理论证。
3、能运用三角形的内角、外角性质定理进行解答或证明有关几何问题。
一、阅读课本P14-15, 回答下列问题
1、三角形的外角的定义是什么?
2、三角形的外角等于 。
3、三角形的外角大于 。
4、三角形的外角和等于 度
5、完成课本第15-16页练习
三角形的外角
A
B
C
D
∠ACD是△ABC的一个外角
三角形的一边与另一边的延长线组成的角,叫做三角形的外角.
E
一个三角形共有几个外角
校对课本P15-16练习
完成课本P16 T5,6,7
8字形特殊规律
A
B
C
D
O
1、把图中∠1、 ∠2、 ∠3按由大到小的顺序排列
B
3
2
1
A
C
D
E
∠1
∠2
∠3
>
>
效果检测
课本P13 T1
2、如图,D是△ABC的BC边上一点,
∠B=∠BAD,∠ADC=80°,∠BAC=70°.
求:(1)∠B的度数;
(2)∠C的度数.
A
B
C
D
80°
70°
3、如图,在△ABC中,已知AD是角平分线,
DE⊥AC,∠B=66°,∠C=54°
求∠ADE的度数.
效果检测
40°
70°
60°
4.如图,一个直角三角形纸板,剪去直角后,得到一个四边形,则∠1+∠2= 。
x
y
5.把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则∠A与∠1+∠2之间有一种数量关系 。
四边形不相邻两外角之和等于不相邻内角之和
6.在五角星中,
∠A+∠B+∠C+∠D+∠E= .
小亮从A点出发,沿直线前进10米后
最终回到了A点,他共走了 米。
7.某零件如图所示,图纸要求∠A=90°,
∠B=32°,∠BDC=145°∠C= .
∠B、∠C、∠BDC 、∠A三角之间有何关系
E
8.如图是一副三角尺拼成的图案,则∠AEB= .
效果测试
9.如图,求∠A+∠B+∠C+∠D+∠E的度数.(至少两种方法)
F
10.如图,求:∠A+∠B+∠C+
∠D+∠E+∠F= .
11.一副三角板有两个直角三角形,如图叠放在一起,则∠α的度数是= .
12.如图2,∠1+∠2+∠3+∠ 4的值为 .
13.如图,求:∠A+∠B+∠C+∠D+∠E+∠F= .
14.如图,求∠A +∠B +∠C +∠D+∠E +∠F的度数
特殊图形中角的转化问题
截角五角星
15.如图,则∠A+∠B+∠C+∠D+∠E+∠F=______.
16.(1)如图(1),在△ABC中,∠A=α,∠ABC的平分线与
∠ACD的平分线交于点A1得∠A1,求∠A1的度数。
(2)如图(2),∠A1BC的平分线与∠A1CD的平分线交于
点A2,得∠A2 ,…, 则∠An= .
17. 则∠A、∠B、∠C与∠BDC之间有一种数量关系 。
凹角等于不相邻它的三个内角之和
17. 则AP,CP为角平分线,则∠D、∠B、与∠P之间有一种数量关系 。
8字形,两上角之和等于两下角之和
2、《全品》P9-10
课后作业
