高中数学必修第一册人教A版(2019)4.5.2《用二分法求方程的近似解》名师课件(共25张PPT)
文档属性
| 名称 | 高中数学必修第一册人教A版(2019)4.5.2《用二分法求方程的近似解》名师课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-07 00:00:00 | ||
图片预览







文档简介
(共25张PPT)
函数的零点定义:
对于函数y=f(x),我们把使f(x)=0的实数x,叫做函数y=f(x)的零点.
函数零点的求解
方程f(x)=0的根
代数法
函数y=f(x)的图象与x轴交点的横坐标
图象法
等价关系:
方程f(x)=0有实数根
函数y=f(x)的图象与x轴有交点
函数y=f(x)有零点
复习引入
人教A版同步教材名师课件
用二分法求方程的近似解
学习目标
学 习 目 标 核心素养
能借助计算工具用二分法求方程的近似解. 数学运算
学习目标
课程目标
1.了解二分法的原理及其适用条件.
2.掌握二分法的实施步骤.
3.通过用二分法求方程的近似解,使学生体会函数零点与方程根之间的联系,初步形成用函数观点处理问题的意识.
数学学科素养
1.数学抽象:二分法的概念;
2.逻辑推理:用二分法求函数零点近似值的步骤;
3.数学运算:求函数零点近似值;
4.数学建模:通过一些函数模型的实例,让学生感受建立函数模型的过程和方法,体会函数在数学和其他学科中的广泛应用.
猜价格,规则如下:
(1)价格是0至80元之间的整数;
(2)与正确价格误差不超过2元时算猜对
(3)只能给出“高了”、“低了”的提示
问题1:每次猜出一个价格时,大家给出“高了”、“低了”的提示起什么作用?
不断缩小范围,逼近正确价格
问题2:如果限制时间和次数,那么一般情况下怎样猜才能更快的猜对呢?
每次取中点,将范围缩小一半
探究新知
上述过程可以归纳如下:
(1)确定范围和误差要求
(2)取中点
(3)①可能中点正好是正确价格,
②也可能不是,这时要再次确定范围,
重复前两步,就可以不断缩小范围,
逼近正确价格,直到猜对为止。
探究新知
求下列方程的解:
对于(1),很容易求出方程的解;对于方程(2)就不好求出具体的解.参考上面的猜价格游戏规则,来研究方程(2)的解.
探究新知
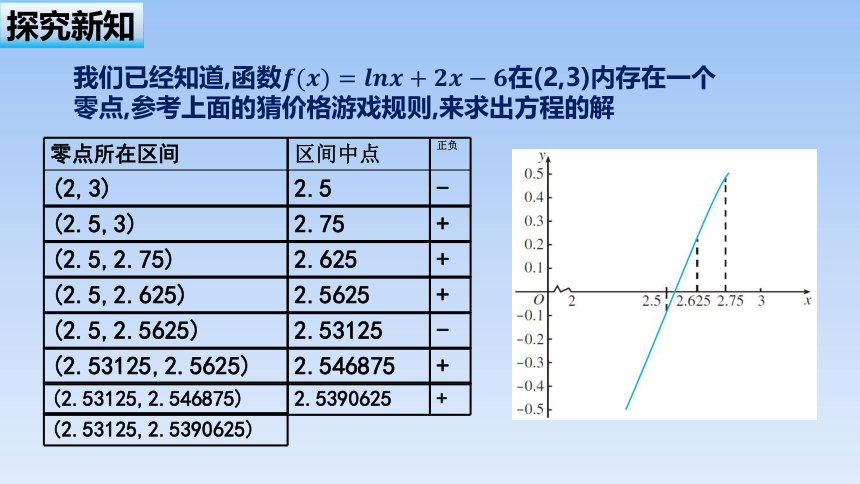
零点所在区间
(2,3)
区间中点
2.5
正负
-
我们已经知道,函数在(2,3)内存在一个零点,参考上面的猜价格游戏规则,来求出方程的解
(2.5,3)
2.75
+
(2.5,2.75)
(2.5,2.625)
(2.5,2.5625)
(2.53125,2.5625)
(2.53125,2.546875)
(2.53125,2.5390625)
2.625
2.5625
2.53125
2.546875
2.5390625
+
+
-
+
+
探究新知
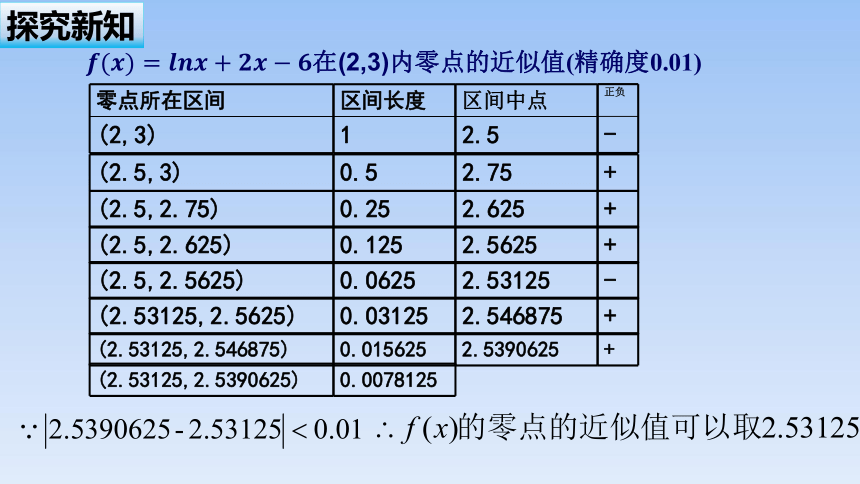
零点所在区间
(2,3)
区间中点
2.5
正负
-
在(2,3)内零点的近似值(精确度0.01)
区间长度
1
(2.5,3)
0.5
2.75
+
(2.5,2.75)
(2.5,2.625)
(2.5,2.5625)
(2.53125,2.5625)
(2.53125,2.546875)
(2.53125,2.5390625)
0.25
0.125
0.0625
0.03125
0.015625
0.0078125
2.625
2.5625
2.53125
2.546875
2.5390625
+
+
-
+
+
探究新知
探究新知
例如,当精确度为0.01时,因为|2.5390625-2.53125|=0.0078125<0.01,所以区间(2.53125,2.5390625)内任意一点都可以作为零点的近似值,也可以将 =2.53125作为函数零点的近似值,也即方程0的近似解.
对于在区间上图象连续不断且的函数,通过不断地把它的零点所在区间一分为二,使所得区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫做二分法(bisection).
(3)计算
(1)确定区间 ,验证 ,给定精确度 ;
(2)求区间 的 c;
①若 ,则 ;
②若 ,则令 ,此时零点
③若 ,则令 ,此时零点
(4)判断是否达到精确度 :即若 ,则得
到零点近似值 ;否则重复(2)~(4).
二分法求函数零点的近似值的一般步骤如下:
探究新知
例1、借助信息技术,用二分法求方程的近似解(精确度为0.1).
原方程即,令,用信息技术画出函数的图象并列出它的对应值表:
解析
典例讲解
例1、借助信息技术,用二分法求方程的近似解(精确度为0.1).
解析
典例讲解
观察图或表,可知,说明该函数在区间(1,2)内存在零点.取区间(1,2)的中点=1.5,用信息技术算得.因为,所以再取区间的中点=1.25,用信息技术算得因为,所以 同理可得,∈(1.375,1.5),∈( 1.375 , 1.4375 ).由于|1.375 - 1.4375|=0.0625<0.1, 所以,原方程的近似解可取为1.375 .
周而复始怎么办 精确度上来判断.
定区间,找中点,中值计算两边看.
同号去,异号算,零点落在异号间.
方法归纳
典例讲解
例2、 求方程 的近似解 (精确度为 0.1) .
解析
做出与的图象,如图所示
由函数与的图像可知,方程有唯一实数解,且在区间内.
设,用计算器计算,列表如下
典例讲解
例2、 求方程 的近似解 (精确度为 0.1) .
解析
取值区间 中点值 中点函数 近似值 区间长度
(0,1) 0.5 -0.0081 1
(0.5,1) 0.75 0.2805 0.5
(0.5,0.75) 0.625 0.1475 0.25
(0.5,0.625) 0.5625 0.073 0.125
由于区间 (0.5,0.625) 的长度为 0.125<0.2, 此时该区间中点0.5625与真正零点的误差不超过0.1,所以函数的零点的一个近似值为0.5625,即方程的近似解为 0.5625.
方法归纳
当二分法的精度要求很高时,手算会十分困难,所以高精度需求下的二分法仅在计算机上实现,并且这也只是一种近似算法,仅能用来确定零点的范围, 不能用来求解零点.
方法归纳
定区间
列表
下结论
估计方程的解所在的初始区问 (一般采用估值法完成)
把计算结果列表表示,不断缩小范围
写出方程的近似解
方法归纳
用数形结合的思想寻找解题思路,具体体现为:①由数化形,由条件绘制相关图形,使图形能充分反映出它们的数量关系,从而解决问题;②由形化数,借助图形,通过观察研究,找出图形中蕴含的数量关系,反映出事物的本质特征;③数形转换,化抽象为直观,化难为易.
变式训练
1.利用二分法求关于 的方程 的正实数解的近似值(精确度为0.1).
解析
令,则关于的方程的正实数解的近似值即为函数 ( )= 的正零点的近似值.
由于,故可取区间作为计算的初始区间用二分法逐次计算,列表如下:
区间 中点的值 中点函数值
(或近似值 )
(2,3) 2.5 0.25
(2,2.5) 2.25 -0.4375
(2.25,2.5) 2.375 -0.10938
(2.375,2.5) 2.4375 0.066406
(2.375,2.4375) 2.40625 -0.02246
因为,所以关于的方程的正实数解的近似值可取.
当堂练习
下列关于函数 的命题中,正确的是 ( )
A、若 且满足 则 是 的一个零点
B、若 是 在 上的零点,则可以用二分法求 的近似值
C、函数 的零点是方程 的根,但 的根不一定是函数 的零点
D 、用二分法求方程的根时,得到的都是近似解
A
2.用二分法求图象是连续不断的函数在 内零点近似值的过程中得到 ,则函数的零点落在下面哪个区间内 ( )
A 、 B 、 C 、 D 、不能确定
A
当堂练习
3.用二分法研究函数 的零点时,第一次经计算得,可得其中一个零点 _____,第二次应计算_____.以上横线上应填的内容分别为 ( )
A、 B、 C、 D 、
B
4.若函数 的一个零点 (正数) 附近的函数值用二分法逐次计算,参考数据如下表:
那么方程 的一个近似解(精确度为0.04)为 ( )
A 、 B 、 C 、 D 、
D
当堂练习
5.已知曲线 与直线 的交点的横坐标是 ,则 的取值范围是( )
A 、 B 、 C 、 D 、
A
归纳小结
二分法
用二分法求函数零点
近似值的步骤
用二分法求给定精确
度的方程的近似解
二分法的定义
作 业
P145:4、5
函数的零点定义:
对于函数y=f(x),我们把使f(x)=0的实数x,叫做函数y=f(x)的零点.
函数零点的求解
方程f(x)=0的根
代数法
函数y=f(x)的图象与x轴交点的横坐标
图象法
等价关系:
方程f(x)=0有实数根
函数y=f(x)的图象与x轴有交点
函数y=f(x)有零点
复习引入
人教A版同步教材名师课件
用二分法求方程的近似解
学习目标
学 习 目 标 核心素养
能借助计算工具用二分法求方程的近似解. 数学运算
学习目标
课程目标
1.了解二分法的原理及其适用条件.
2.掌握二分法的实施步骤.
3.通过用二分法求方程的近似解,使学生体会函数零点与方程根之间的联系,初步形成用函数观点处理问题的意识.
数学学科素养
1.数学抽象:二分法的概念;
2.逻辑推理:用二分法求函数零点近似值的步骤;
3.数学运算:求函数零点近似值;
4.数学建模:通过一些函数模型的实例,让学生感受建立函数模型的过程和方法,体会函数在数学和其他学科中的广泛应用.
猜价格,规则如下:
(1)价格是0至80元之间的整数;
(2)与正确价格误差不超过2元时算猜对
(3)只能给出“高了”、“低了”的提示
问题1:每次猜出一个价格时,大家给出“高了”、“低了”的提示起什么作用?
不断缩小范围,逼近正确价格
问题2:如果限制时间和次数,那么一般情况下怎样猜才能更快的猜对呢?
每次取中点,将范围缩小一半
探究新知
上述过程可以归纳如下:
(1)确定范围和误差要求
(2)取中点
(3)①可能中点正好是正确价格,
②也可能不是,这时要再次确定范围,
重复前两步,就可以不断缩小范围,
逼近正确价格,直到猜对为止。
探究新知
求下列方程的解:
对于(1),很容易求出方程的解;对于方程(2)就不好求出具体的解.参考上面的猜价格游戏规则,来研究方程(2)的解.
探究新知
零点所在区间
(2,3)
区间中点
2.5
正负
-
我们已经知道,函数在(2,3)内存在一个零点,参考上面的猜价格游戏规则,来求出方程的解
(2.5,3)
2.75
+
(2.5,2.75)
(2.5,2.625)
(2.5,2.5625)
(2.53125,2.5625)
(2.53125,2.546875)
(2.53125,2.5390625)
2.625
2.5625
2.53125
2.546875
2.5390625
+
+
-
+
+
探究新知
零点所在区间
(2,3)
区间中点
2.5
正负
-
在(2,3)内零点的近似值(精确度0.01)
区间长度
1
(2.5,3)
0.5
2.75
+
(2.5,2.75)
(2.5,2.625)
(2.5,2.5625)
(2.53125,2.5625)
(2.53125,2.546875)
(2.53125,2.5390625)
0.25
0.125
0.0625
0.03125
0.015625
0.0078125
2.625
2.5625
2.53125
2.546875
2.5390625
+
+
-
+
+
探究新知
探究新知
例如,当精确度为0.01时,因为|2.5390625-2.53125|=0.0078125<0.01,所以区间(2.53125,2.5390625)内任意一点都可以作为零点的近似值,也可以将 =2.53125作为函数零点的近似值,也即方程0的近似解.
对于在区间上图象连续不断且的函数,通过不断地把它的零点所在区间一分为二,使所得区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫做二分法(bisection).
(3)计算
(1)确定区间 ,验证 ,给定精确度 ;
(2)求区间 的 c;
①若 ,则 ;
②若 ,则令 ,此时零点
③若 ,则令 ,此时零点
(4)判断是否达到精确度 :即若 ,则得
到零点近似值 ;否则重复(2)~(4).
二分法求函数零点的近似值的一般步骤如下:
探究新知
例1、借助信息技术,用二分法求方程的近似解(精确度为0.1).
原方程即,令,用信息技术画出函数的图象并列出它的对应值表:
解析
典例讲解
例1、借助信息技术,用二分法求方程的近似解(精确度为0.1).
解析
典例讲解
观察图或表,可知,说明该函数在区间(1,2)内存在零点.取区间(1,2)的中点=1.5,用信息技术算得.因为,所以再取区间的中点=1.25,用信息技术算得因为,所以 同理可得,∈(1.375,1.5),∈( 1.375 , 1.4375 ).由于|1.375 - 1.4375|=0.0625<0.1, 所以,原方程的近似解可取为1.375 .
周而复始怎么办 精确度上来判断.
定区间,找中点,中值计算两边看.
同号去,异号算,零点落在异号间.
方法归纳
典例讲解
例2、 求方程 的近似解 (精确度为 0.1) .
解析
做出与的图象,如图所示
由函数与的图像可知,方程有唯一实数解,且在区间内.
设,用计算器计算,列表如下
典例讲解
例2、 求方程 的近似解 (精确度为 0.1) .
解析
取值区间 中点值 中点函数 近似值 区间长度
(0,1) 0.5 -0.0081 1
(0.5,1) 0.75 0.2805 0.5
(0.5,0.75) 0.625 0.1475 0.25
(0.5,0.625) 0.5625 0.073 0.125
由于区间 (0.5,0.625) 的长度为 0.125<0.2, 此时该区间中点0.5625与真正零点的误差不超过0.1,所以函数的零点的一个近似值为0.5625,即方程的近似解为 0.5625.
方法归纳
当二分法的精度要求很高时,手算会十分困难,所以高精度需求下的二分法仅在计算机上实现,并且这也只是一种近似算法,仅能用来确定零点的范围, 不能用来求解零点.
方法归纳
定区间
列表
下结论
估计方程的解所在的初始区问 (一般采用估值法完成)
把计算结果列表表示,不断缩小范围
写出方程的近似解
方法归纳
用数形结合的思想寻找解题思路,具体体现为:①由数化形,由条件绘制相关图形,使图形能充分反映出它们的数量关系,从而解决问题;②由形化数,借助图形,通过观察研究,找出图形中蕴含的数量关系,反映出事物的本质特征;③数形转换,化抽象为直观,化难为易.
变式训练
1.利用二分法求关于 的方程 的正实数解的近似值(精确度为0.1).
解析
令,则关于的方程的正实数解的近似值即为函数 ( )= 的正零点的近似值.
由于,故可取区间作为计算的初始区间用二分法逐次计算,列表如下:
区间 中点的值 中点函数值
(或近似值 )
(2,3) 2.5 0.25
(2,2.5) 2.25 -0.4375
(2.25,2.5) 2.375 -0.10938
(2.375,2.5) 2.4375 0.066406
(2.375,2.4375) 2.40625 -0.02246
因为,所以关于的方程的正实数解的近似值可取.
当堂练习
下列关于函数 的命题中,正确的是 ( )
A、若 且满足 则 是 的一个零点
B、若 是 在 上的零点,则可以用二分法求 的近似值
C、函数 的零点是方程 的根,但 的根不一定是函数 的零点
D 、用二分法求方程的根时,得到的都是近似解
A
2.用二分法求图象是连续不断的函数在 内零点近似值的过程中得到 ,则函数的零点落在下面哪个区间内 ( )
A 、 B 、 C 、 D 、不能确定
A
当堂练习
3.用二分法研究函数 的零点时,第一次经计算得,可得其中一个零点 _____,第二次应计算_____.以上横线上应填的内容分别为 ( )
A、 B、 C、 D 、
B
4.若函数 的一个零点 (正数) 附近的函数值用二分法逐次计算,参考数据如下表:
那么方程 的一个近似解(精确度为0.04)为 ( )
A 、 B 、 C 、 D 、
D
当堂练习
5.已知曲线 与直线 的交点的横坐标是 ,则 的取值范围是( )
A 、 B 、 C 、 D 、
A
归纳小结
二分法
用二分法求函数零点
近似值的步骤
用二分法求给定精确
度的方程的近似解
二分法的定义
作 业
P145:4、5
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
