圆心角与圆周角的关系[上学期]
文档属性
| 名称 | 圆心角与圆周角的关系[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 549.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-11-05 16:28:00 | ||
图片预览



文档简介
课件34张PPT。www.1230.org 初中数学资源网
圆23.1.3. 圆周角和圆心角的关系
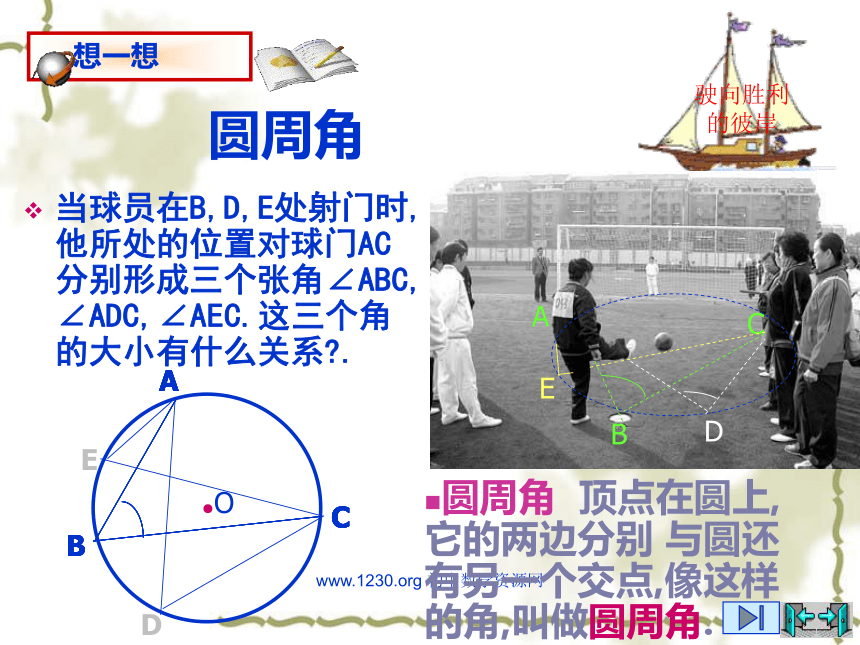
-圆周角定理www.1230.org 初中数学资源网圆周角在射门游戏中(如图),球员射中球门的难易程度与他所处的位置B对球门AC的张角(∠ABC)有关.驶向胜利的彼岸圆周角 顶点在圆上,它的两边分别 与圆还有另一个交点,像这样的角,叫做圆周角.www.1230.org 初中数学资源网圆周角当球员在B,D,E处射门时,他所处的位置对球门AC分别形成三个张角∠ABC, ∠ADC,∠AEC.这三个角的大小有什么关系?.驶向胜利的彼岸圆周角 顶点在圆上,它的两边分别 与圆还有另一个交点,像这样的角,叫做圆周角.www.1230.org 初中数学资源网特征:① 角的顶点在圆上.② 角的两边都与圆相交.圆周角定义: 顶点在圆上,
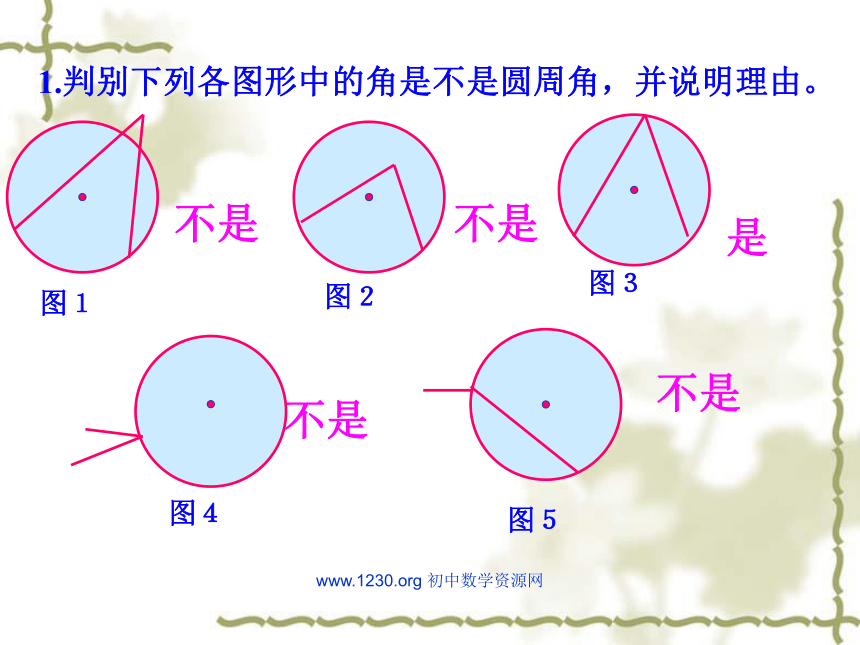
并且两边都和圆相交的角叫圆周角.4Awww.1230.org 初中数学资源网1.判别下列各图形中的角是不是圆周角,并说明理由。不是不是是不是不是图1图2图3图4图5www.1230.org 初中数学资源网 练一练
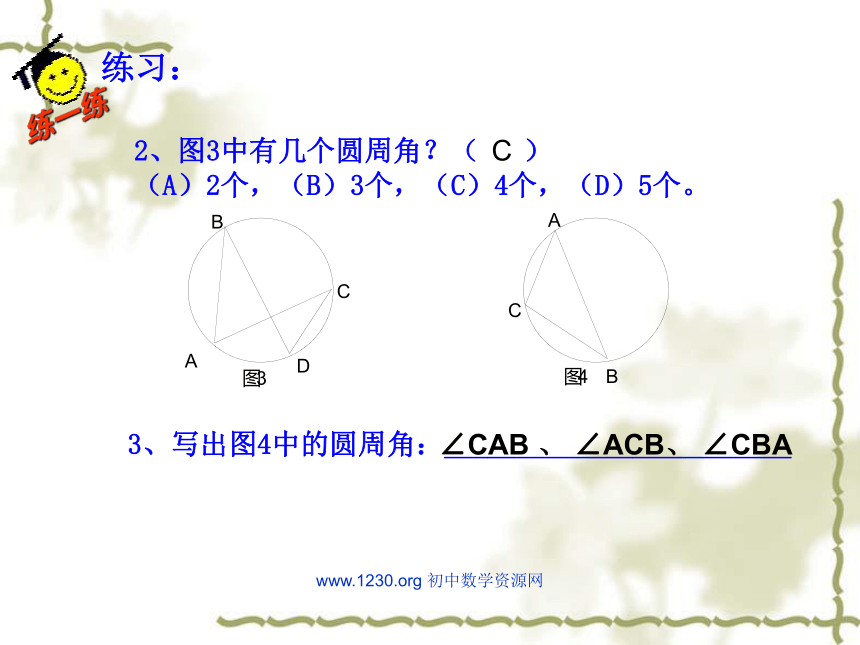
2、图3中有几个圆周角?( )
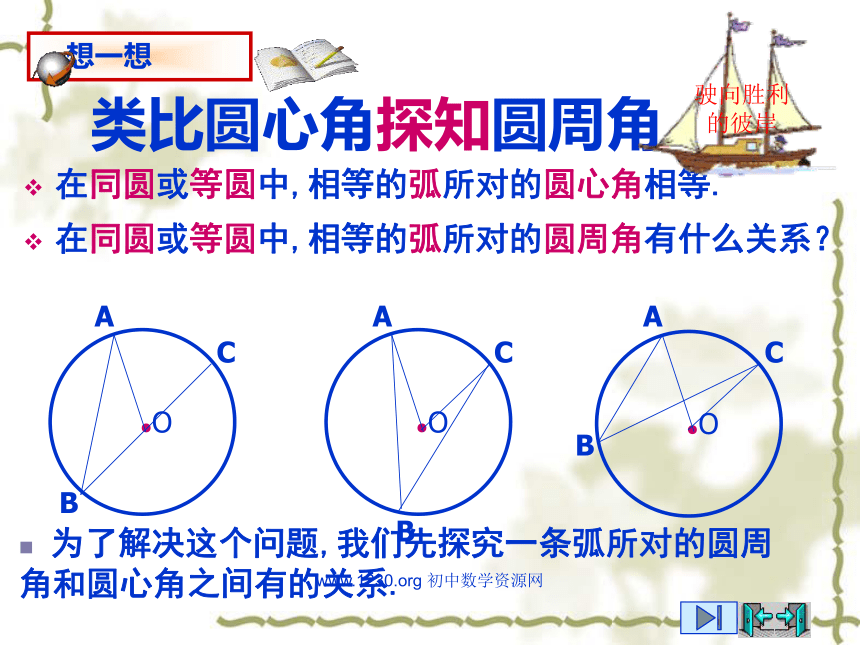
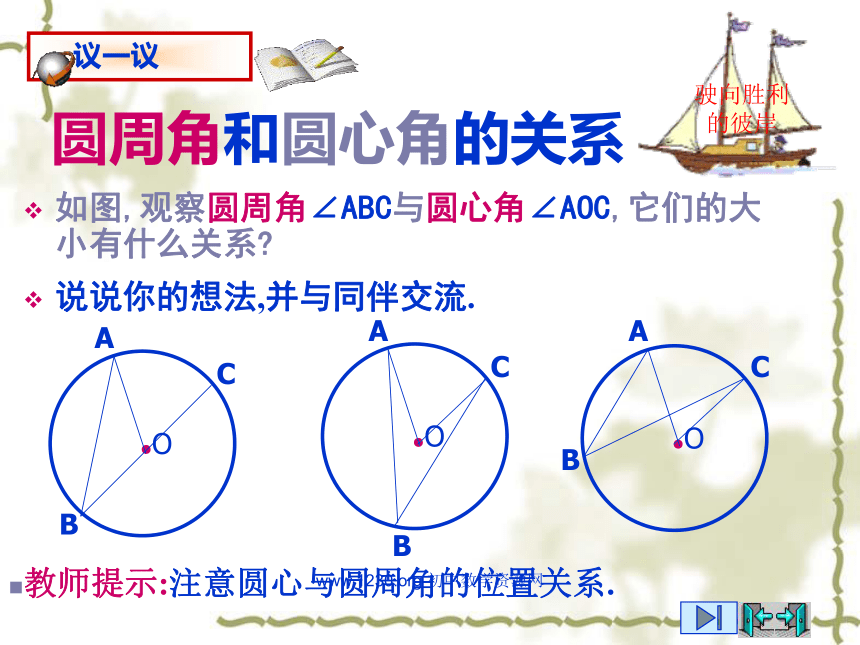
(A)2个,(B)3个,(C)4个,(D)5个。3、写出图4中的圆周角:________________________C∠CAB 、 ∠ACB、 ∠CBA练习:www.1230.org 初中数学资源网类比圆心角探知圆周角在同圆或等圆中,相等的弧所对的圆心角相等.在同圆或等圆中,相等的弧所对的圆周角有什么关系?驶向胜利的彼岸 为了解决这个问题,我们先探究一条弧所对的圆周角和圆心角之间有的关系.www.1230.org 初中数学资源网圆周角和圆心角的关系如图,观察圆周角∠ABC与圆心角∠AOC,它们的大小有什么关系?说说你的想法,并与同伴交流.驶向胜利的彼岸教师提示:注意圆心与圆周角的位置关系.www.1230.org 初中数学资源网驶向胜利的彼岸圆周角和圆心角的关系1.首先考虑一种特殊情况:
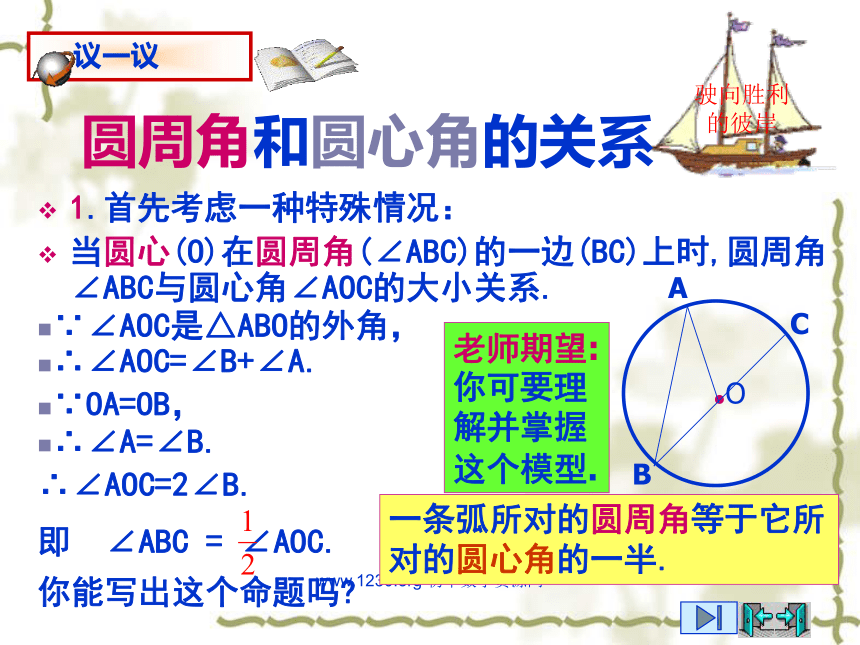
当圆心(O)在圆周角(∠ABC)的一边(BC)上时,圆周角∠ABC与圆心角∠AOC的大小关系.∵∠AOC是△ABO的外角,∴∠AOC=∠B+∠A.∵OA=OB,∴∠A=∠B.∴∠AOC=2∠B.即 ∠ABC = ∠AOC.你能写出这个命题吗?一条弧所对的圆周角等于它所对的圆心角的一半.老师期望:你可要理解并掌握这个模型.www.1230.org 初中数学资源网驶向胜利的彼岸圆周角和圆心角的关系如果圆心不在圆周角的一边上,结果会怎样?
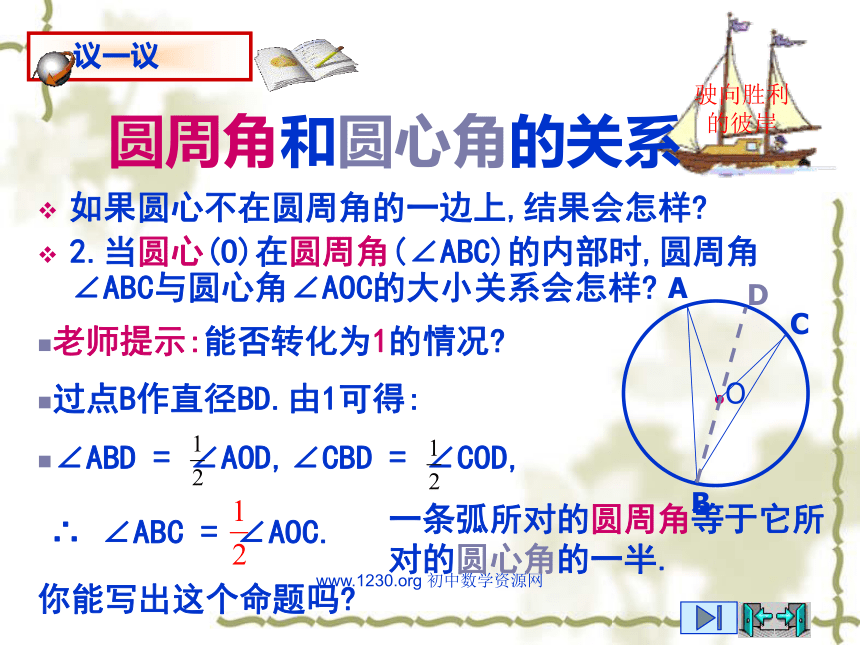
2.当圆心(O)在圆周角(∠ABC)的内部时,圆周角∠ABC与圆心角∠AOC的大小关系会怎样?老师提示:能否转化为1的情况?过点B作直径BD.由1可得: ∴ ∠ABC = ∠AOC.你能写出这个命题吗?一条弧所对的圆周角等于它所对的圆心角的一半.∠ABD = ∠AOD,∠CBD = ∠COD,www.1230.org 初中数学资源网驶向胜利的彼岸圆周角和圆心角的关系如果圆心不在圆周角的一边上,结果会怎样?
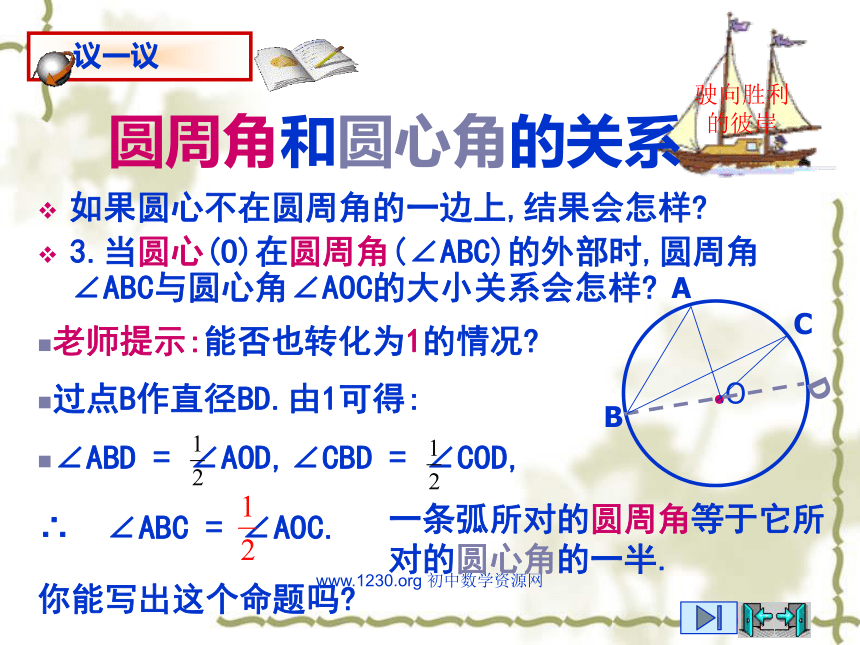
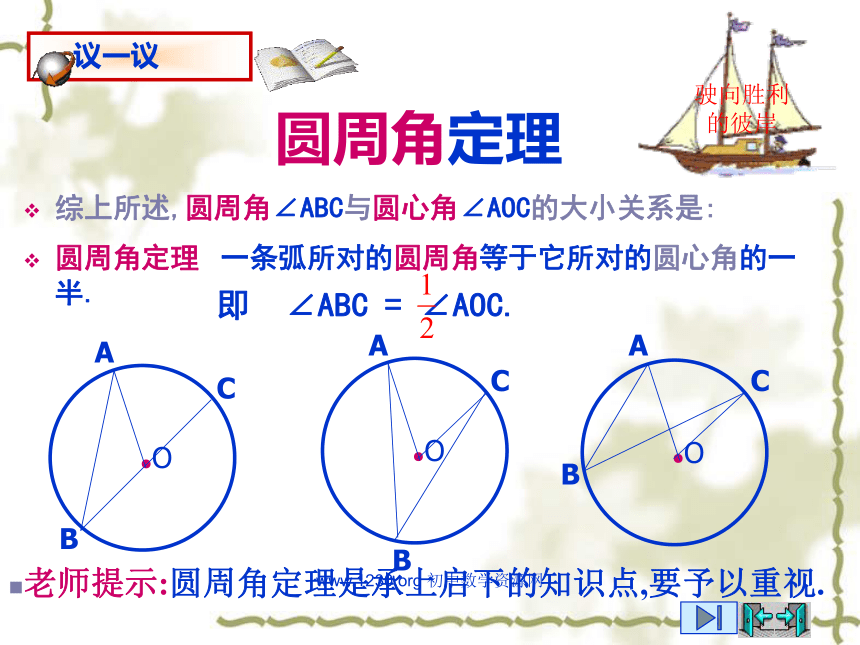
3.当圆心(O)在圆周角(∠ABC)的外部时,圆周角∠ABC与圆心角∠AOC的大小关系会怎样?老师提示:能否也转化为1的情况?过点B作直径BD.由1可得:∴ ∠ABC = ∠AOC.你能写出这个命题吗?一条弧所对的圆周角等于它所对的圆心角的一半.∠ABD = ∠AOD,∠CBD = ∠COD,www.1230.org 初中数学资源网圆周角定理综上所述,圆周角∠ABC与圆心角∠AOC的大小关系是:圆周角定理 一条弧所对的圆周角等于它所对的圆心角的一半.驶向胜利的彼岸老师提示:圆周角定理是承上启下的知识点,要予以重视.即 ∠ABC = ∠AOC.www.1230.org 初中数学资源网驶向胜利的彼岸思考与巩固1.如图,在⊙O中,∠BOC=50°,求∠A的大小. 2.举出生活中含有圆周角的例子.解: ∠A = ∠BOC = 25°.www.1230.org 初中数学资源网驶向胜利的彼岸拓展 化心动为行动1.如图(1),在⊙O中,∠BAD=50°,求∠C的大小.2.如图(2),在⊙O中,∠B,∠D,∠E的大小有什么关系?为什么?
3.如图(3),AB是直径,你能确定∠C的度数吗?CABDBACDE(1) (2) (3)www.1230.org 初中数学资源网圆周角定理:
一条弧所对的圆周角等于它所对的圆心角的一半。ABCO定理: 在同圆或等圆中,
同弧或等弧所对的圆周角相等,
都等于该弧所对的圆心角的一半。 BCDEAwww.1230.org 初中数学资源网探究活动:有关圆周角的度数 1. 探究半圆或直径所对的圆周角 等于多少度? 2.90°的圆周角所对的弦是否是直径?线段AB是⊙O的直径,点C是⊙O上任意一点(除点A、B), 那 么,∠ACB就是直径AB所对的圆周角.想想看,∠ACB会是怎么样的角?为什么呢?www.1230.org 初中数学资源网证明:
因为OA=OB=OC,所以△AOC、△BOC都是等腰三角形,所以∠OAC=∠OCA,∠OBC=∠OCB. 又 ∠OAC+∠OBC+∠ACB=180°,所以 ∠ACB=∠OCA+∠OCB=90°.因此,不管点C在⊙O上何处(除点A、B),∠ACB总等于90°,即:
结论:
半圆或直径所对的圆周角都相等,都等于90°(直角)。反过来也是成立的,即90°的圆周角所对的弦是圆的直径www.1230.org 初中数学资源网问题解答1、圆周角定理的推论1:同圆或等圆中,同弧或等弧所对的圆周角相等;
同圆或等圆中,相等的圆周角所对的弧也相等。2、圆周角定理的推论2:半圆(或直径)所对的圆周角是直角;
90°的圆周角所对的弦是直径。用于找相等的角用于找相等的弧用于判断某个圆周角是否是直角用于判断某条线是否过圆心www.1230.org 初中数学资源网1、圆心角与所对的弧的关系2、圆周角与所对的弧的关系3、同弧所对的圆心角与圆周角的关系探究:圆周角的度数等于它所对弧的度数的一半。圆心角的度数等于它所对弧的度数。同弧所对的圆周角等于该弧所对圆心角的一半www.1230.org 初中数学资源网做做看,收获知多少?一、判断
1、顶点在圆上的角叫圆周角。( )
2、圆周角的度数等于所对弧的度数的一半。( )
二、计算
半径为R的圆中,有一弦分圆周成1:2两部分,则弦所对的
圆周角的度数是 。×√.O60°或120°www.1230.org 初中数学资源网1、100o的弧所对的圆心角等于_______,所对的圆周角等于_______。
2、一弦分圆周角成两部分,其中一部分是另一部分的4倍,则这弦所对的圆周角度数为________________。
3、如图,在⊙O中,∠BAC=32o,则∠BOC=________。
4、如图,⊙O中,∠ACB = 130o,则∠AOB=______。
5、下列命题中是真命题的是( )
(A)顶点在圆周上的角叫做圆周角。
(B)60o的圆周角所对的弧的度数是30o
(C)一弧所对的圆周角等于它所对的圆心角。
(D)120o的弧所对的圆周角是60oB
100o50o36o或144o64o100oD练习www.1230.org 初中数学资源网2.如图,圆心角∠AOB=100°,则∠ACB=___。1.求圆中角X的度数130° C C D Bwww.1230.org 初中数学资源网DABC例题如图;四边形ABCD的四个顶点在⊙O上。
求证;∠B+∠D = 180°
Owww.1230.org 初中数学资源网OABC已知:OA、OB、OC都是⊙O的半径,
∠AOB=2∠BOC
求证:∠ACB= 2 ∠BAC 证明:www.1230.org 初中数学资源网例2已知:如图,在△ABC中,AB=AC,
以AB为直径的圆交BC于D,交AC于E,
求证:⌒ ⌒BD=DE证明:连结AD.∵AB是圆的直径,点D在圆上,∴∠ADB=90°,∴AD⊥BC,∵AB=AC,∴AD平分顶角∠BAC,即∠BAD=∠CAD,∴ ⌒ ⌒BD= DE(同圆或等圆中,相等的圆周角所对弧相等)。www.1230.org 初中数学资源网练习:如图,P是△ABC的外接圆上的一点∠APC=∠CPB=60°。求证:△ABC是等边三角形证明:∵∠ABC和∠APC
都是⌒所对的圆周角。 AC∴∠ABC=∠APC=60°(同弧所对的圆周角相等)同理,∵∠BAC和∠CPB都是⌒所对的圆周角,BC∴∠BAC=∠CPB=60°。∴△ABC等边三角形。www.1230.org 初中数学资源网例4:一个圆形人工湖,弦AB是湖上的一座桥,已知桥AB长100m.测得圆周角∠C=45°求这个人工湖的直径.ABCwww.1230.org 初中数学资源网例4:一个圆形人工湖,弦AB是湖上的一座桥,已知桥AB长100m.测得圆周角∠C=45°求这个人工湖的直径.ABCDwww.1230.org 初中数学资源网练一练:1.说出命题’圆的两条平行弦所夹的弧相等”的逆命题.原命题和逆命题都是真命题吗?请说明理由.2.已知:四边形ABCD内接于圆,BD平分∠ABC,且AB∥CD.求证:AD=BCwww.1230.org 初中数学资源网想一想:如图:AB是⊙O的直径,弦CD⊥AB于点E,G是⌒上任意一点,延长AG,与DC的延长线相交于点F,连接AD,GD,CG,找出图中所有和∠ADC相等的角,并说明理由.ACwww.1230.org 初中数学资源网1如图,⊙O中,AB是直径,半径CO⊥AB,D是CO的中点,DE // AB,求证: ∠COE=2 ∠AOE.提高拓展:www.1230.org 初中数学资源网例3: 船在航行过程中,船长常常通过测定角度来确定是否会遇到暗礁。如图A,B表示灯塔,暗礁分布在经过A,B两点的一个圆形区域内,C表示一个危险临界点,∠ACB就是“危险角”,当船与两个灯塔的夹角大于“危险角”时,就有可能触礁。弓形所含的圆周角∠C=50°,问船在航行时怎样才能保证不进入暗礁区?www.1230.org 初中数学资源网(1)当船与两个灯塔的夹角∠α大于“危险角”时,船位于哪个区域?为什么?(2)当船与两个灯塔的夹角∠α小于“危险角”时,船位于哪个区域?为什么?www.1230.org 初中数学资源网结束寄语要养成用数学的语言去说明道理,用数学的思维去解读世界的习惯.再见
-圆周角定理www.1230.org 初中数学资源网圆周角在射门游戏中(如图),球员射中球门的难易程度与他所处的位置B对球门AC的张角(∠ABC)有关.驶向胜利的彼岸圆周角 顶点在圆上,它的两边分别 与圆还有另一个交点,像这样的角,叫做圆周角.www.1230.org 初中数学资源网圆周角当球员在B,D,E处射门时,他所处的位置对球门AC分别形成三个张角∠ABC, ∠ADC,∠AEC.这三个角的大小有什么关系?.驶向胜利的彼岸圆周角 顶点在圆上,它的两边分别 与圆还有另一个交点,像这样的角,叫做圆周角.www.1230.org 初中数学资源网特征:① 角的顶点在圆上.② 角的两边都与圆相交.圆周角定义: 顶点在圆上,
并且两边都和圆相交的角叫圆周角.4Awww.1230.org 初中数学资源网1.判别下列各图形中的角是不是圆周角,并说明理由。不是不是是不是不是图1图2图3图4图5www.1230.org 初中数学资源网 练一练
2、图3中有几个圆周角?( )
(A)2个,(B)3个,(C)4个,(D)5个。3、写出图4中的圆周角:________________________C∠CAB 、 ∠ACB、 ∠CBA练习:www.1230.org 初中数学资源网类比圆心角探知圆周角在同圆或等圆中,相等的弧所对的圆心角相等.在同圆或等圆中,相等的弧所对的圆周角有什么关系?驶向胜利的彼岸 为了解决这个问题,我们先探究一条弧所对的圆周角和圆心角之间有的关系.www.1230.org 初中数学资源网圆周角和圆心角的关系如图,观察圆周角∠ABC与圆心角∠AOC,它们的大小有什么关系?说说你的想法,并与同伴交流.驶向胜利的彼岸教师提示:注意圆心与圆周角的位置关系.www.1230.org 初中数学资源网驶向胜利的彼岸圆周角和圆心角的关系1.首先考虑一种特殊情况:
当圆心(O)在圆周角(∠ABC)的一边(BC)上时,圆周角∠ABC与圆心角∠AOC的大小关系.∵∠AOC是△ABO的外角,∴∠AOC=∠B+∠A.∵OA=OB,∴∠A=∠B.∴∠AOC=2∠B.即 ∠ABC = ∠AOC.你能写出这个命题吗?一条弧所对的圆周角等于它所对的圆心角的一半.老师期望:你可要理解并掌握这个模型.www.1230.org 初中数学资源网驶向胜利的彼岸圆周角和圆心角的关系如果圆心不在圆周角的一边上,结果会怎样?
2.当圆心(O)在圆周角(∠ABC)的内部时,圆周角∠ABC与圆心角∠AOC的大小关系会怎样?老师提示:能否转化为1的情况?过点B作直径BD.由1可得: ∴ ∠ABC = ∠AOC.你能写出这个命题吗?一条弧所对的圆周角等于它所对的圆心角的一半.∠ABD = ∠AOD,∠CBD = ∠COD,www.1230.org 初中数学资源网驶向胜利的彼岸圆周角和圆心角的关系如果圆心不在圆周角的一边上,结果会怎样?
3.当圆心(O)在圆周角(∠ABC)的外部时,圆周角∠ABC与圆心角∠AOC的大小关系会怎样?老师提示:能否也转化为1的情况?过点B作直径BD.由1可得:∴ ∠ABC = ∠AOC.你能写出这个命题吗?一条弧所对的圆周角等于它所对的圆心角的一半.∠ABD = ∠AOD,∠CBD = ∠COD,www.1230.org 初中数学资源网圆周角定理综上所述,圆周角∠ABC与圆心角∠AOC的大小关系是:圆周角定理 一条弧所对的圆周角等于它所对的圆心角的一半.驶向胜利的彼岸老师提示:圆周角定理是承上启下的知识点,要予以重视.即 ∠ABC = ∠AOC.www.1230.org 初中数学资源网驶向胜利的彼岸思考与巩固1.如图,在⊙O中,∠BOC=50°,求∠A的大小. 2.举出生活中含有圆周角的例子.解: ∠A = ∠BOC = 25°.www.1230.org 初中数学资源网驶向胜利的彼岸拓展 化心动为行动1.如图(1),在⊙O中,∠BAD=50°,求∠C的大小.2.如图(2),在⊙O中,∠B,∠D,∠E的大小有什么关系?为什么?
3.如图(3),AB是直径,你能确定∠C的度数吗?CABDBACDE(1) (2) (3)www.1230.org 初中数学资源网圆周角定理:
一条弧所对的圆周角等于它所对的圆心角的一半。ABCO定理: 在同圆或等圆中,
同弧或等弧所对的圆周角相等,
都等于该弧所对的圆心角的一半。 BCDEAwww.1230.org 初中数学资源网探究活动:有关圆周角的度数 1. 探究半圆或直径所对的圆周角 等于多少度? 2.90°的圆周角所对的弦是否是直径?线段AB是⊙O的直径,点C是⊙O上任意一点(除点A、B), 那 么,∠ACB就是直径AB所对的圆周角.想想看,∠ACB会是怎么样的角?为什么呢?www.1230.org 初中数学资源网证明:
因为OA=OB=OC,所以△AOC、△BOC都是等腰三角形,所以∠OAC=∠OCA,∠OBC=∠OCB. 又 ∠OAC+∠OBC+∠ACB=180°,所以 ∠ACB=∠OCA+∠OCB=90°.因此,不管点C在⊙O上何处(除点A、B),∠ACB总等于90°,即:
结论:
半圆或直径所对的圆周角都相等,都等于90°(直角)。反过来也是成立的,即90°的圆周角所对的弦是圆的直径www.1230.org 初中数学资源网问题解答1、圆周角定理的推论1:同圆或等圆中,同弧或等弧所对的圆周角相等;
同圆或等圆中,相等的圆周角所对的弧也相等。2、圆周角定理的推论2:半圆(或直径)所对的圆周角是直角;
90°的圆周角所对的弦是直径。用于找相等的角用于找相等的弧用于判断某个圆周角是否是直角用于判断某条线是否过圆心www.1230.org 初中数学资源网1、圆心角与所对的弧的关系2、圆周角与所对的弧的关系3、同弧所对的圆心角与圆周角的关系探究:圆周角的度数等于它所对弧的度数的一半。圆心角的度数等于它所对弧的度数。同弧所对的圆周角等于该弧所对圆心角的一半www.1230.org 初中数学资源网做做看,收获知多少?一、判断
1、顶点在圆上的角叫圆周角。( )
2、圆周角的度数等于所对弧的度数的一半。( )
二、计算
半径为R的圆中,有一弦分圆周成1:2两部分,则弦所对的
圆周角的度数是 。×√.O60°或120°www.1230.org 初中数学资源网1、100o的弧所对的圆心角等于_______,所对的圆周角等于_______。
2、一弦分圆周角成两部分,其中一部分是另一部分的4倍,则这弦所对的圆周角度数为________________。
3、如图,在⊙O中,∠BAC=32o,则∠BOC=________。
4、如图,⊙O中,∠ACB = 130o,则∠AOB=______。
5、下列命题中是真命题的是( )
(A)顶点在圆周上的角叫做圆周角。
(B)60o的圆周角所对的弧的度数是30o
(C)一弧所对的圆周角等于它所对的圆心角。
(D)120o的弧所对的圆周角是60oB
100o50o36o或144o64o100oD练习www.1230.org 初中数学资源网2.如图,圆心角∠AOB=100°,则∠ACB=___。1.求圆中角X的度数130° C C D Bwww.1230.org 初中数学资源网DABC例题如图;四边形ABCD的四个顶点在⊙O上。
求证;∠B+∠D = 180°
Owww.1230.org 初中数学资源网OABC已知:OA、OB、OC都是⊙O的半径,
∠AOB=2∠BOC
求证:∠ACB= 2 ∠BAC 证明:www.1230.org 初中数学资源网例2已知:如图,在△ABC中,AB=AC,
以AB为直径的圆交BC于D,交AC于E,
求证:⌒ ⌒BD=DE证明:连结AD.∵AB是圆的直径,点D在圆上,∴∠ADB=90°,∴AD⊥BC,∵AB=AC,∴AD平分顶角∠BAC,即∠BAD=∠CAD,∴ ⌒ ⌒BD= DE(同圆或等圆中,相等的圆周角所对弧相等)。www.1230.org 初中数学资源网练习:如图,P是△ABC的外接圆上的一点∠APC=∠CPB=60°。求证:△ABC是等边三角形证明:∵∠ABC和∠APC
都是⌒所对的圆周角。 AC∴∠ABC=∠APC=60°(同弧所对的圆周角相等)同理,∵∠BAC和∠CPB都是⌒所对的圆周角,BC∴∠BAC=∠CPB=60°。∴△ABC等边三角形。www.1230.org 初中数学资源网例4:一个圆形人工湖,弦AB是湖上的一座桥,已知桥AB长100m.测得圆周角∠C=45°求这个人工湖的直径.ABCwww.1230.org 初中数学资源网例4:一个圆形人工湖,弦AB是湖上的一座桥,已知桥AB长100m.测得圆周角∠C=45°求这个人工湖的直径.ABCDwww.1230.org 初中数学资源网练一练:1.说出命题’圆的两条平行弦所夹的弧相等”的逆命题.原命题和逆命题都是真命题吗?请说明理由.2.已知:四边形ABCD内接于圆,BD平分∠ABC,且AB∥CD.求证:AD=BCwww.1230.org 初中数学资源网想一想:如图:AB是⊙O的直径,弦CD⊥AB于点E,G是⌒上任意一点,延长AG,与DC的延长线相交于点F,连接AD,GD,CG,找出图中所有和∠ADC相等的角,并说明理由.ACwww.1230.org 初中数学资源网1如图,⊙O中,AB是直径,半径CO⊥AB,D是CO的中点,DE // AB,求证: ∠COE=2 ∠AOE.提高拓展:www.1230.org 初中数学资源网例3: 船在航行过程中,船长常常通过测定角度来确定是否会遇到暗礁。如图A,B表示灯塔,暗礁分布在经过A,B两点的一个圆形区域内,C表示一个危险临界点,∠ACB就是“危险角”,当船与两个灯塔的夹角大于“危险角”时,就有可能触礁。弓形所含的圆周角∠C=50°,问船在航行时怎样才能保证不进入暗礁区?www.1230.org 初中数学资源网(1)当船与两个灯塔的夹角∠α大于“危险角”时,船位于哪个区域?为什么?(2)当船与两个灯塔的夹角∠α小于“危险角”时,船位于哪个区域?为什么?www.1230.org 初中数学资源网结束寄语要养成用数学的语言去说明道理,用数学的思维去解读世界的习惯.再见
同课章节目录
