圆的综合水平检测试题[上学期]
文档属性
| 名称 | 圆的综合水平检测试题[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 165.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-11-06 00:00:00 | ||
图片预览

文档简介
圆的综合水平检测试题
一、精心选一选
1,如果两圆相交,那么两圆的公切线共有( )
A. 4条 B. 3条 C. 2条 D. 1条
2,下列三个命题:①圆既是轴对称图形,又是中心对称图形;②垂直于弦的直径平分这条弦;③相等圆心角所对的弧相等;其中是真命题的是( )
A.①② B.②③ C.①③ D.①②③
3,如图1,PA、PB是⊙O的两条切线,切点是A、B.如果OP=4,PA=2,那么∠AOB等于( )
A. 90° B. 100° C. 110° D. 120°
4,如图2,AB是⊙O的直径,CD为弦,CD⊥AB于E,则下列结论中不一定成立的是( )
A.∠COE=∠DOE B.CE=DE C.OE=BE D.
5,如果两圆相交,那么两圆的公切线共有( )
A. 4条 B. 3条 C. 2条 D. 1条
6,如图3,一圆内切四边形ABCD,且AB=16,CD=10,则四边形的周长为 ( )
A.50 B.52 C.54 D.56
7,如图4,△ABC是等边三角形,⊙O与AC相切于A点,与BC交于E点,与AB的延长线交于D点.已知BE=6,CE=4,则BD的长为( )
A.10 B.15 C.25 D.9
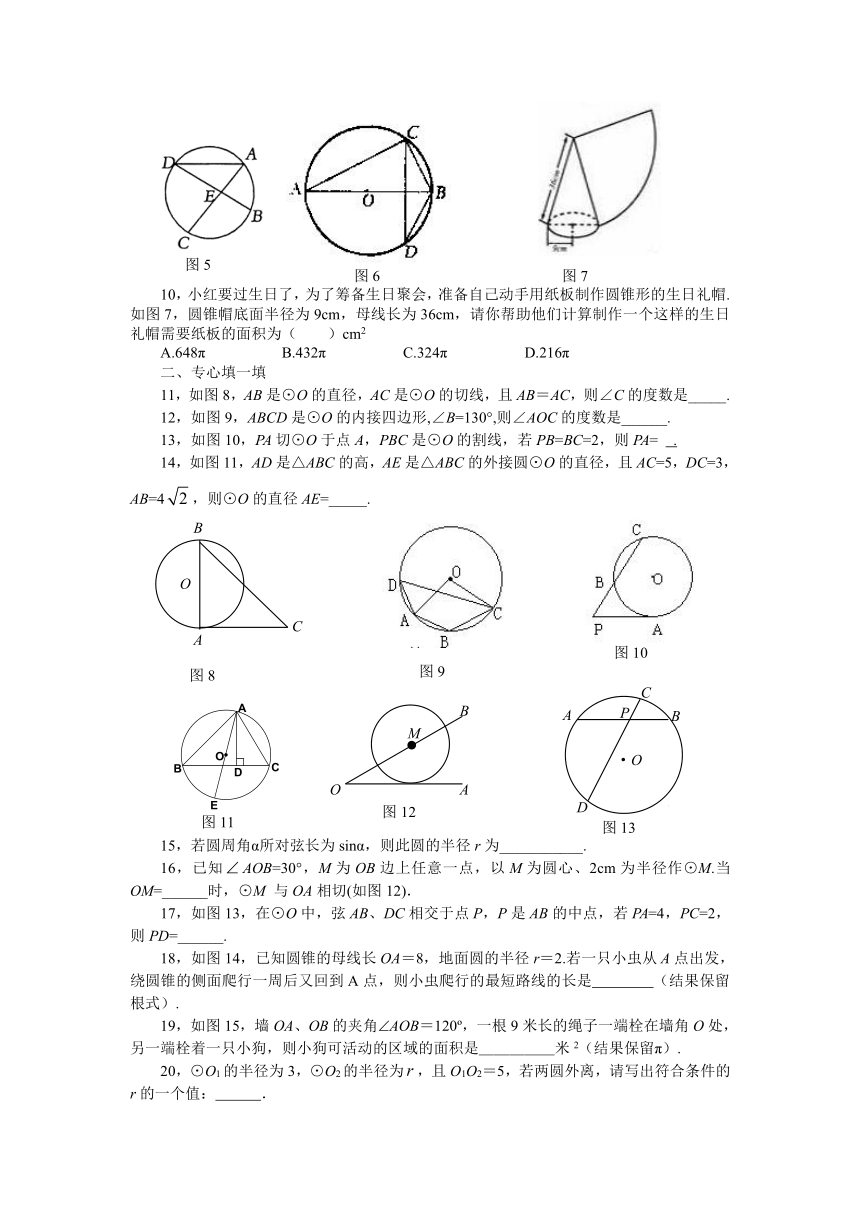
8,如图5,已知∠DEC=80°,弧CD的度数与弧AB的度数的差为20°,则∠DA C的度数为( )
A.35° B.45° C.25° D.50°
9,如图6,已知AB是⊙O的直径,CD是弦且CD⊥AB,BC=6,AC=8,则sin∠ABD的值是( )
A. B. C. D.
10,小红要过生日了,为了筹备生日聚会,准备自己动手用纸板制作圆锥形的生日礼帽.如图7,圆锥帽底面半径为9cm,母线长为36cm,请你帮助他们计算制作一个这样的生日礼帽需要纸板的面积为( )cm2
A.648π B.432π C.324π D.216π
二、专心填一填
11,如图8,AB是⊙O的直径,AC是⊙O的切线,且AB=AC,则∠C的度数是_____.
12,如图9,ABCD是⊙O的内接四边形,∠B=130°,则∠AOC的度数是______.
13,如图10,PA切⊙O于点A,PBC是⊙O的割线,若PB=BC=2,则PA= .
14,如图11,AD是△ABC的高,AE是△ABC的外接圆⊙O的直径,且AC=5,DC=3,AB=4,则⊙O的直径AE=_____.
15,若圆周角α所对弦长为sinα,则此圆的半径r为___________.
16,已知AOB=30°,M为OB边上任意一点,以M为圆心、2cm为半径作⊙M.当OM=______时,⊙M 与OA相切(如图12).
17,如图13,在⊙O中,弦AB、DC相交于点P,P是AB的中点,若PA=4,PC=2,则PD=______.
18,如图14,已知圆锥的母线长OA=8,地面圆的半径r=2.若一只小虫从A点出发,绕圆锥的侧面爬行一周后又回到A点,则小虫爬行的最短路线的长是 (结果保留根式).
19,如图15,墙OA、OB的夹角AOB=120 ,一根9米长的绳子一端栓在墙角O处,另一端栓着一只小狗,则小狗可活动的区域的面积是_____米2(结果保留π).
20,⊙O1的半径为3,⊙O2的半径为,且O1O2=5,若两圆外离,请写出符合条件的r的一个值: .
三、用心做一做
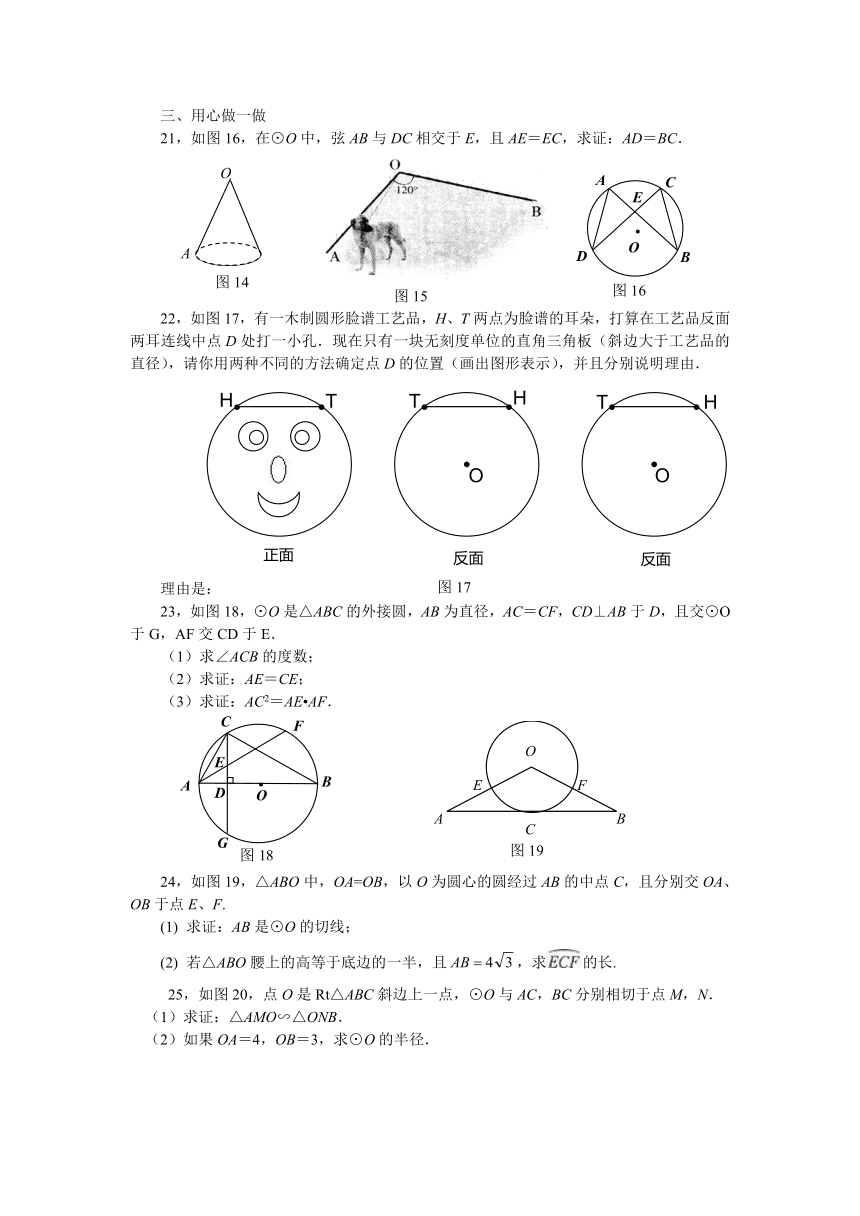
21,如图16,在⊙O中,弦AB与DC相交于E,且AE=EC,求证:AD=BC.
22,如图17,有一木制圆形脸谱工艺品,H、T两点为脸谱的耳朵,打算在工艺品反面两耳连线中点D处打一小孔.现在只有一块无刻度单位的直角三角板(斜边大于工艺品的直径),请你用两种不同的方法确定点D的位置(画出图形表示),并且分别说明理由.
理由是:
23,如图18,⊙O是△ABC的外接圆,AB为直径,AC=CF,CD⊥AB于D,且交⊙O于G,AF交CD于E.
(1)求∠ACB的度数;
(2)求证:AE=CE;
(3)求证:AC2=AE AF.
24,如图19,△ABO中,OA=OB,以O为圆心的圆经过AB的中点C,且分别交OA、OB于点E、F.
(1) 求证:AB是⊙O的切线;
(2) 若△ABO腰上的高等于底边的一半,且,求的长.
25,如图20,点O是Rt△ABC斜边上一点,⊙O与AC,BC分别相切于点M,N.
(1)求证:△AMO∽△ONB.
(2)如果OA=4,OB=3,求⊙O的半径.
26,如图21,已知:AB为⊙O的弦(非直径),E为AB的中点,EO的延长线与⊙O相交于C,CM∥AB,BO的延长线与⊙O相交于F,与CM相交于D.
(1) 求证:EC⊥CD;(2)当EO∶OC=1∶3,CD=4时,求⊙O的半径.
27,如图22,已知四边形ABCD内接于⊙O,A是的中点,AE⊥AC于A,与⊙O及CB的延长线分别交于点F、E,且,EM切⊙O于M.
⑴ △ADC∽△EBA;
⑵ AC2=BC·CE;
⑶ 如果AB=2,EM=3,求cot∠CAD的值.
28,如图23,⊙O1与⊙O2都经过A、B两点,经过点A的直线CD与⊙O1交于点C,与⊙O2交于点D.经过点B的直线EF与⊙O1交于点E,与⊙O2交于点F.
(1)求证:CE∥DF;
(2)在图1中,若CD和EF可以分别绕点A和点B转动,当点C与点E重合时(如图2),过点E作直线MN∥DF,试判断直线MN与⊙O1的位置关系,并证明你的结论.
参考答案:
一、1,C;2,A;3,D;4,C;5,C;6,B;7,D;8,B;9,D;10,C.
二、11,45°;12,100°;13,2;14,5;15,;16,4;17,8;18,;19,27π;20,填0<r<2范围内的任一个数.
三、21,在△AED和△CEB中,因为∠A=∠C,AE=CE,∠AED=∠CEB,所以△AED≌△CEB△AED和△CEB,所以AD=BC.
22,如图:
方法一:如图①,画TH的垂线L交TH于D,则点D就是TH的中点.依据是垂径定理.
方法二:如图②,分别过点T、H画HC⊥TO,TE⊥HO,HC与TE相交于点F,过点O、F画直线L交HT于点D,则点D就是HT的中点.由画图知,Rt△HOC≌Rt△TOE,易得HF=TF,又OH=OT,所以点O、F在HT的中垂线上,所以HD=TD .
方法三:如图③,(原理同方法二).
23,(1)解:∵AB为⊙O的直径,∴∠ACB=90°.(2)证明:∵AB为直径,且AB⊥CG,∴AC=AG, 又∵AC=CF,∴AG=CF,∴∠ACG=∠CAF,∴AE=CE.(3)连结CF,由(2)可知:AG=AC,∴∠ACE=∠AFC ,又∵∠CAE=∠FAC,∴△AEC∽△ACF ,∴,∴AC2=AE·AF.
24,(1)证明:连结OC. ∵OA=OB,AC=BC,∴OC⊥AB.∴AB是⊙O的切线. (2)过B点作BD⊥AO,交AO的延长线于D点.由题意有 AB=2BD,由题目条件,有.在Rt△ABD中,根据正弦定义∴∠A=30°. 在Rt△ACO中,,∠A=30°,则AO=2OC.由勾股定理,求得 OC=2. ∵OA=OB,且∠A=30°,∴∠AOB=120°.由弧长公式可求得的长为.
25,(1)证明:∵ ⊙O与AC,BC分别相切于点M,N,∴O M⊥AC,ON⊥BC.在△AMO和△ONB中, ∠AMO=∠ONB.又∵BC⊥AC,即OM∥BC,∠AOM=∠OBN.故 △AMO∽△ONB. (2)∵ OM∥CN,ON∥CM,OM=ON,∠C是直角,即四边形CMON是正方形.设⊙O的半径为r,即OM=ON=CM=CN=r.在Rt△AMO中,AM=.又∵△AMO∽△ONB,∴.故,解得:.即⊙O的半径是.
26,(1)因为E为弦AB(非直径)的中点,O为圆心,所以∠BEO=90°,因为CD∥AB,所以∠OCD=90°,即EC⊥CD.(2)因为CD∥AB,EO:OC=1:3,所以BO:OD=1:3,设OC=BO=x,则OD=3 x,又CD=4,在Rt△OCD中,由OC2+CD2=OD2,得x2+42=(3 x)2,解得x1=,x2=-(舍去),所以BO=,即⊙O的半径为.
27,⑴∵四边形ABCD内接于⊙O,∴∠CDA=∠ABE,∵ ,∴∠DCA=∠BAE,∴△CAD∽△AEB;⑵过A作AH⊥BC于H,∵A是中点,∴HC=HB=BC,∵∠CAE=90°,∴AC2=CH·CE=BC·CE;⑶∵A是中点,AB=2,∴AC=AB=2,∵EM是⊙O的切线,∴EB·EC=EM2 ①,∵AC2=BC·CE,BC·CE=8 ②,由①+②得:EC(EB+BC)=17,∴EC2=17,∵EC2=AC2+AE2,∴AE=,∵△CAD∽△ABE,∴∠CAD=∠AEC,∴cot∠CAD=cot∠AEC=;
28,(1)在图1中连结AB,因为ABEC是⊙O1的内接四边形,所以∠BAD=∠E.又ADFB是⊙O2的内接四边形,所以∠BAD+∠F=180°,即∠E+∠F=180°,所以CE∥DF;(2)MN与⊙O1相切,在图2中过E作⊙O1的直径EH,连结AH和AB,因为MN∥DF,所以∠MEA=∠D,又因为∠D=∠ABE=∠AHE,所以∠MEA=∠AHE,因为EH为⊙O1的直径,所以∠EAH=90°,所以∠AHE+∠AEH=90°,即∠MEA+∠AEH=90°,又因为EH为⊙O1的直径,所以MN为⊙O1的切线.
图2
C
D
A
O
B
E
B
A
O
图12
图20
C
B
C
F
图4
图23
G
图6
图5
O
M
C
B
D
O
E
A
图21
图1
图22
图17
图9
·O
D
P
B
C
A
图14
A
图
图8
O
C
B
A
D
A
O
图18
图11
图7
图15
图13
图19
图3
·
E
O
D
图16
C
B
A
图10
E
·
B
O
N
M
A
一、精心选一选
1,如果两圆相交,那么两圆的公切线共有( )
A. 4条 B. 3条 C. 2条 D. 1条
2,下列三个命题:①圆既是轴对称图形,又是中心对称图形;②垂直于弦的直径平分这条弦;③相等圆心角所对的弧相等;其中是真命题的是( )
A.①② B.②③ C.①③ D.①②③
3,如图1,PA、PB是⊙O的两条切线,切点是A、B.如果OP=4,PA=2,那么∠AOB等于( )
A. 90° B. 100° C. 110° D. 120°
4,如图2,AB是⊙O的直径,CD为弦,CD⊥AB于E,则下列结论中不一定成立的是( )
A.∠COE=∠DOE B.CE=DE C.OE=BE D.
5,如果两圆相交,那么两圆的公切线共有( )
A. 4条 B. 3条 C. 2条 D. 1条
6,如图3,一圆内切四边形ABCD,且AB=16,CD=10,则四边形的周长为 ( )
A.50 B.52 C.54 D.56
7,如图4,△ABC是等边三角形,⊙O与AC相切于A点,与BC交于E点,与AB的延长线交于D点.已知BE=6,CE=4,则BD的长为( )
A.10 B.15 C.25 D.9
8,如图5,已知∠DEC=80°,弧CD的度数与弧AB的度数的差为20°,则∠DA C的度数为( )
A.35° B.45° C.25° D.50°
9,如图6,已知AB是⊙O的直径,CD是弦且CD⊥AB,BC=6,AC=8,则sin∠ABD的值是( )
A. B. C. D.
10,小红要过生日了,为了筹备生日聚会,准备自己动手用纸板制作圆锥形的生日礼帽.如图7,圆锥帽底面半径为9cm,母线长为36cm,请你帮助他们计算制作一个这样的生日礼帽需要纸板的面积为( )cm2
A.648π B.432π C.324π D.216π
二、专心填一填
11,如图8,AB是⊙O的直径,AC是⊙O的切线,且AB=AC,则∠C的度数是_____.
12,如图9,ABCD是⊙O的内接四边形,∠B=130°,则∠AOC的度数是______.
13,如图10,PA切⊙O于点A,PBC是⊙O的割线,若PB=BC=2,则PA= .
14,如图11,AD是△ABC的高,AE是△ABC的外接圆⊙O的直径,且AC=5,DC=3,AB=4,则⊙O的直径AE=_____.
15,若圆周角α所对弦长为sinα,则此圆的半径r为___________.
16,已知AOB=30°,M为OB边上任意一点,以M为圆心、2cm为半径作⊙M.当OM=______时,⊙M 与OA相切(如图12).
17,如图13,在⊙O中,弦AB、DC相交于点P,P是AB的中点,若PA=4,PC=2,则PD=______.
18,如图14,已知圆锥的母线长OA=8,地面圆的半径r=2.若一只小虫从A点出发,绕圆锥的侧面爬行一周后又回到A点,则小虫爬行的最短路线的长是 (结果保留根式).
19,如图15,墙OA、OB的夹角AOB=120 ,一根9米长的绳子一端栓在墙角O处,另一端栓着一只小狗,则小狗可活动的区域的面积是_____米2(结果保留π).
20,⊙O1的半径为3,⊙O2的半径为,且O1O2=5,若两圆外离,请写出符合条件的r的一个值: .
三、用心做一做
21,如图16,在⊙O中,弦AB与DC相交于E,且AE=EC,求证:AD=BC.
22,如图17,有一木制圆形脸谱工艺品,H、T两点为脸谱的耳朵,打算在工艺品反面两耳连线中点D处打一小孔.现在只有一块无刻度单位的直角三角板(斜边大于工艺品的直径),请你用两种不同的方法确定点D的位置(画出图形表示),并且分别说明理由.
理由是:
23,如图18,⊙O是△ABC的外接圆,AB为直径,AC=CF,CD⊥AB于D,且交⊙O于G,AF交CD于E.
(1)求∠ACB的度数;
(2)求证:AE=CE;
(3)求证:AC2=AE AF.
24,如图19,△ABO中,OA=OB,以O为圆心的圆经过AB的中点C,且分别交OA、OB于点E、F.
(1) 求证:AB是⊙O的切线;
(2) 若△ABO腰上的高等于底边的一半,且,求的长.
25,如图20,点O是Rt△ABC斜边上一点,⊙O与AC,BC分别相切于点M,N.
(1)求证:△AMO∽△ONB.
(2)如果OA=4,OB=3,求⊙O的半径.
26,如图21,已知:AB为⊙O的弦(非直径),E为AB的中点,EO的延长线与⊙O相交于C,CM∥AB,BO的延长线与⊙O相交于F,与CM相交于D.
(1) 求证:EC⊥CD;(2)当EO∶OC=1∶3,CD=4时,求⊙O的半径.
27,如图22,已知四边形ABCD内接于⊙O,A是的中点,AE⊥AC于A,与⊙O及CB的延长线分别交于点F、E,且,EM切⊙O于M.
⑴ △ADC∽△EBA;
⑵ AC2=BC·CE;
⑶ 如果AB=2,EM=3,求cot∠CAD的值.
28,如图23,⊙O1与⊙O2都经过A、B两点,经过点A的直线CD与⊙O1交于点C,与⊙O2交于点D.经过点B的直线EF与⊙O1交于点E,与⊙O2交于点F.
(1)求证:CE∥DF;
(2)在图1中,若CD和EF可以分别绕点A和点B转动,当点C与点E重合时(如图2),过点E作直线MN∥DF,试判断直线MN与⊙O1的位置关系,并证明你的结论.
参考答案:
一、1,C;2,A;3,D;4,C;5,C;6,B;7,D;8,B;9,D;10,C.
二、11,45°;12,100°;13,2;14,5;15,;16,4;17,8;18,;19,27π;20,填0<r<2范围内的任一个数.
三、21,在△AED和△CEB中,因为∠A=∠C,AE=CE,∠AED=∠CEB,所以△AED≌△CEB△AED和△CEB,所以AD=BC.
22,如图:
方法一:如图①,画TH的垂线L交TH于D,则点D就是TH的中点.依据是垂径定理.
方法二:如图②,分别过点T、H画HC⊥TO,TE⊥HO,HC与TE相交于点F,过点O、F画直线L交HT于点D,则点D就是HT的中点.由画图知,Rt△HOC≌Rt△TOE,易得HF=TF,又OH=OT,所以点O、F在HT的中垂线上,所以HD=TD .
方法三:如图③,(原理同方法二).
23,(1)解:∵AB为⊙O的直径,∴∠ACB=90°.(2)证明:∵AB为直径,且AB⊥CG,∴AC=AG, 又∵AC=CF,∴AG=CF,∴∠ACG=∠CAF,∴AE=CE.(3)连结CF,由(2)可知:AG=AC,∴∠ACE=∠AFC ,又∵∠CAE=∠FAC,∴△AEC∽△ACF ,∴,∴AC2=AE·AF.
24,(1)证明:连结OC. ∵OA=OB,AC=BC,∴OC⊥AB.∴AB是⊙O的切线. (2)过B点作BD⊥AO,交AO的延长线于D点.由题意有 AB=2BD,由题目条件,有.在Rt△ABD中,根据正弦定义∴∠A=30°. 在Rt△ACO中,,∠A=30°,则AO=2OC.由勾股定理,求得 OC=2. ∵OA=OB,且∠A=30°,∴∠AOB=120°.由弧长公式可求得的长为.
25,(1)证明:∵ ⊙O与AC,BC分别相切于点M,N,∴O M⊥AC,ON⊥BC.在△AMO和△ONB中, ∠AMO=∠ONB.又∵BC⊥AC,即OM∥BC,∠AOM=∠OBN.故 △AMO∽△ONB. (2)∵ OM∥CN,ON∥CM,OM=ON,∠C是直角,即四边形CMON是正方形.设⊙O的半径为r,即OM=ON=CM=CN=r.在Rt△AMO中,AM=.又∵△AMO∽△ONB,∴.故,解得:.即⊙O的半径是.
26,(1)因为E为弦AB(非直径)的中点,O为圆心,所以∠BEO=90°,因为CD∥AB,所以∠OCD=90°,即EC⊥CD.(2)因为CD∥AB,EO:OC=1:3,所以BO:OD=1:3,设OC=BO=x,则OD=3 x,又CD=4,在Rt△OCD中,由OC2+CD2=OD2,得x2+42=(3 x)2,解得x1=,x2=-(舍去),所以BO=,即⊙O的半径为.
27,⑴∵四边形ABCD内接于⊙O,∴∠CDA=∠ABE,∵ ,∴∠DCA=∠BAE,∴△CAD∽△AEB;⑵过A作AH⊥BC于H,∵A是中点,∴HC=HB=BC,∵∠CAE=90°,∴AC2=CH·CE=BC·CE;⑶∵A是中点,AB=2,∴AC=AB=2,∵EM是⊙O的切线,∴EB·EC=EM2 ①,∵AC2=BC·CE,BC·CE=8 ②,由①+②得:EC(EB+BC)=17,∴EC2=17,∵EC2=AC2+AE2,∴AE=,∵△CAD∽△ABE,∴∠CAD=∠AEC,∴cot∠CAD=cot∠AEC=;
28,(1)在图1中连结AB,因为ABEC是⊙O1的内接四边形,所以∠BAD=∠E.又ADFB是⊙O2的内接四边形,所以∠BAD+∠F=180°,即∠E+∠F=180°,所以CE∥DF;(2)MN与⊙O1相切,在图2中过E作⊙O1的直径EH,连结AH和AB,因为MN∥DF,所以∠MEA=∠D,又因为∠D=∠ABE=∠AHE,所以∠MEA=∠AHE,因为EH为⊙O1的直径,所以∠EAH=90°,所以∠AHE+∠AEH=90°,即∠MEA+∠AEH=90°,又因为EH为⊙O1的直径,所以MN为⊙O1的切线.
图2
C
D
A
O
B
E
B
A
O
图12
图20
C
B
C
F
图4
图23
G
图6
图5
O
M
C
B
D
O
E
A
图21
图1
图22
图17
图9
·O
D
P
B
C
A
图14
A
图
图8
O
C
B
A
D
A
O
图18
图11
图7
图15
图13
图19
图3
·
E
O
D
图16
C
B
A
图10
E
·
B
O
N
M
A
同课章节目录
