24.2.2 直线与圆的位置关系(2)[下学期]
文档属性
| 名称 | 24.2.2 直线与圆的位置关系(2)[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 301.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-11-07 10:04:00 | ||
图片预览





文档简介
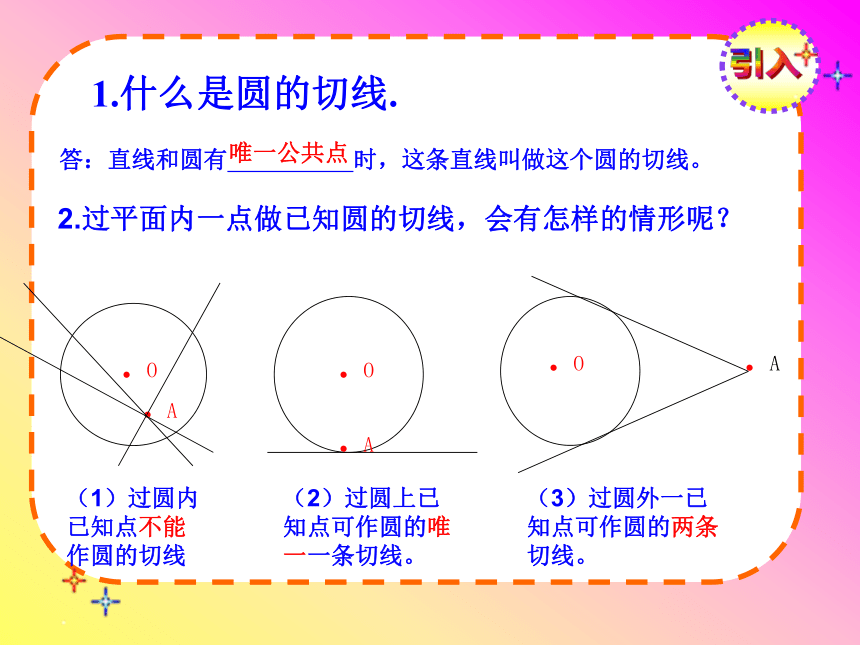
课件15张PPT。24.2.2直线与圆的位置关系(3)制作:罗昭强引入1.什么是圆的切线.
.A.O.A.O.A.O(1)过圆内已知点不能作圆的切线(2)过圆上已知点可作圆的唯一一条切线。(3)过圆外一已知点可作圆的两条切线。答:直线和圆有 时,这条直线叫做这个圆的切线。 2.过平面内一点做已知圆的切线,会有怎样的情形呢?唯一公共点理解切线长:在经过圆外一点的圆的切线上,这点和切点之间的线段的长,叫做这点到圆的切线长。切线长定理:从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角。.Po..A.B几何语言表示为:∵ ,
∴ , .PA,PB为⊙0的切线PA=PBOP平分∠APB12探索如图所示:P是⊙O处一点,PA 、PB为⊙O 的切线,A 和B是切点,直线OP交AB于D,交⊙O于E、F则图中:
(1)共有 对相等线段(圆的半径除外);
(2)共有 对相等的劣弧;
(3)共有 个直角三角形,全等的有____对.
(4)共有 个等腰三角形。
(5)写出图中所有的垂直关系_______________________2262如果PA=4cm,PD=2cm,求半径OA的长。3运用已知:⊙O的半径为3厘米,点P和圆心O的距离OP=6厘米,经过点P和⊙O的两条切线分别为PA、PB,求这两条切线的夹角及切线长。解:连结OA,由切线性质定理得
OA⊥PA,
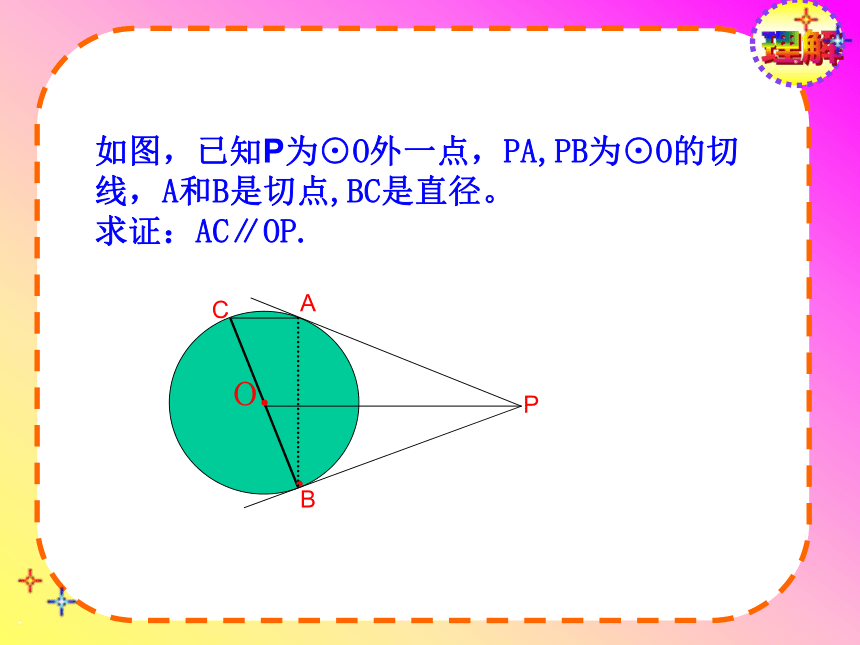
在Rt△POA,∵OA=3,OP=6 理解如图,已知P为⊙O外一点,PA,PB为⊙O的切线,A和B是切点,BC是直径。
求证:AC∥OP.运用.ABCabcrr =a+b-c2直角三角形的两直角边分别是5cm,
12cm 则其内切圆的半径为______。运用如图,在△ABC中,BC=14cm,AC=9cm,AB=13cm,它的内切圆分别和BC,AC,AB切于点D,E,F,求AF,BD和CE的长。解:∵AB,AC分别切⊙O于F,E.∴AF=AE同理:BF=BD,CD=CE设AF=x,BD=y,CE=Z.答:切线长AF=4厘米,BD=9厘米,CE=5厘米。理解2:圆外切四边形的两组对边的和相等。如图:已知四边形ABCD的边AB,BC,CD,DA和⊙o分
别相切于点L,M,N,P
求证:AB+CD=AD+BC证明:∵AB,BC,CD,DA都和⊙o相切,
L,M,N,P是切点∴AL=AP, BL=BM, CN=CM,DN=DP,∴AL+BL+CN+DN=AP+BM+CM+DP
=AP+DP+MB+MC
即
AB+CD=AD+BC圆的外切四边形的两组对边的和相等。运用例:等腰梯形各边都与⊙O相切, ⊙O的直径为6cm,等腰梯形的腰等于8cm,则梯形的面积为_____。868运用DCEO如图:从⊙O外的定点P作⊙O
的两条切线,分别切⊙O于点A
和B, ⑵ ∠DOE的大小是定值 在弧AB上任取一点C,过
点C作⊙O的切线,分别交PA、
PB于点D、E。试证:⑴ △PDE的周长
是定值(PA+PB)(∠AOB/2)若∠P=40°,你能说出∠DOE的度数吗?运用BF如图:AE、BF分别切⊙O于A、B,且AE∥BF,EF切⊙O于C。试证:⑴ AB是⊙O的直径⑵ OE⊥OF ⑶ OC是AE、BF的比例中项⑷ 若⊙O 的半径为6,点C分半圆为1:2两部分,求AE、BF的长。
若以BF、BA所在的直线分别为x轴、y轴,B为原点,请求出EF所在直线的函数解析式。 xy回顾1、判断题:
(1)圆的切线长就是切线的长度。( )
(2)过任一点总可以作圆的两条切线。( )
(3)从圆外一点引圆的两条切线,它们的切线长相等。( )
(4)圆外一点和圆心的连线平分从这点引出的圆的两条切线的夹角( )
(5)圆的外切四边形的两组对边的和相等。( )××√√ √ 2、填空:已知⊙O的半径为3cm,点P和圆心O的距离为6cm,经过点P有⊙ O的两条切线,则切线长为______cm。这两条切线的夹角为_____度。60回顾1.切线长:在经过圆外一点的圆的切线上,这点和切点之间的线段的长,叫做这点到圆的切线长。2.切线长定理:从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角。几何语言表示为:
∵ PA,PB为⊙0的切线,
∴ PA=PB , OP平分∠APB。再见
.A.O.A.O.A.O(1)过圆内已知点不能作圆的切线(2)过圆上已知点可作圆的唯一一条切线。(3)过圆外一已知点可作圆的两条切线。答:直线和圆有 时,这条直线叫做这个圆的切线。 2.过平面内一点做已知圆的切线,会有怎样的情形呢?唯一公共点理解切线长:在经过圆外一点的圆的切线上,这点和切点之间的线段的长,叫做这点到圆的切线长。切线长定理:从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角。.Po..A.B几何语言表示为:∵ ,
∴ , .PA,PB为⊙0的切线PA=PBOP平分∠APB12探索如图所示:P是⊙O处一点,PA 、PB为⊙O 的切线,A 和B是切点,直线OP交AB于D,交⊙O于E、F则图中:
(1)共有 对相等线段(圆的半径除外);
(2)共有 对相等的劣弧;
(3)共有 个直角三角形,全等的有____对.
(4)共有 个等腰三角形。
(5)写出图中所有的垂直关系_______________________2262如果PA=4cm,PD=2cm,求半径OA的长。3运用已知:⊙O的半径为3厘米,点P和圆心O的距离OP=6厘米,经过点P和⊙O的两条切线分别为PA、PB,求这两条切线的夹角及切线长。解:连结OA,由切线性质定理得
OA⊥PA,
在Rt△POA,∵OA=3,OP=6 理解如图,已知P为⊙O外一点,PA,PB为⊙O的切线,A和B是切点,BC是直径。
求证:AC∥OP.运用.ABCabcrr =a+b-c2直角三角形的两直角边分别是5cm,
12cm 则其内切圆的半径为______。运用如图,在△ABC中,BC=14cm,AC=9cm,AB=13cm,它的内切圆分别和BC,AC,AB切于点D,E,F,求AF,BD和CE的长。解:∵AB,AC分别切⊙O于F,E.∴AF=AE同理:BF=BD,CD=CE设AF=x,BD=y,CE=Z.答:切线长AF=4厘米,BD=9厘米,CE=5厘米。理解2:圆外切四边形的两组对边的和相等。如图:已知四边形ABCD的边AB,BC,CD,DA和⊙o分
别相切于点L,M,N,P
求证:AB+CD=AD+BC证明:∵AB,BC,CD,DA都和⊙o相切,
L,M,N,P是切点∴AL=AP, BL=BM, CN=CM,DN=DP,∴AL+BL+CN+DN=AP+BM+CM+DP
=AP+DP+MB+MC
即
AB+CD=AD+BC圆的外切四边形的两组对边的和相等。运用例:等腰梯形各边都与⊙O相切, ⊙O的直径为6cm,等腰梯形的腰等于8cm,则梯形的面积为_____。868运用DCEO如图:从⊙O外的定点P作⊙O
的两条切线,分别切⊙O于点A
和B, ⑵ ∠DOE的大小是定值 在弧AB上任取一点C,过
点C作⊙O的切线,分别交PA、
PB于点D、E。试证:⑴ △PDE的周长
是定值(PA+PB)(∠AOB/2)若∠P=40°,你能说出∠DOE的度数吗?运用BF如图:AE、BF分别切⊙O于A、B,且AE∥BF,EF切⊙O于C。试证:⑴ AB是⊙O的直径⑵ OE⊥OF ⑶ OC是AE、BF的比例中项⑷ 若⊙O 的半径为6,点C分半圆为1:2两部分,求AE、BF的长。
若以BF、BA所在的直线分别为x轴、y轴,B为原点,请求出EF所在直线的函数解析式。 xy回顾1、判断题:
(1)圆的切线长就是切线的长度。( )
(2)过任一点总可以作圆的两条切线。( )
(3)从圆外一点引圆的两条切线,它们的切线长相等。( )
(4)圆外一点和圆心的连线平分从这点引出的圆的两条切线的夹角( )
(5)圆的外切四边形的两组对边的和相等。( )××√√ √ 2、填空:已知⊙O的半径为3cm,点P和圆心O的距离为6cm,经过点P有⊙ O的两条切线,则切线长为______cm。这两条切线的夹角为_____度。60回顾1.切线长:在经过圆外一点的圆的切线上,这点和切点之间的线段的长,叫做这点到圆的切线长。2.切线长定理:从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角。几何语言表示为:
∵ PA,PB为⊙0的切线,
∴ PA=PB , OP平分∠APB。再见
同课章节目录
