13.3.1等腰三角形性质1 课件(共23张PPT)
文档属性
| 名称 | 13.3.1等腰三角形性质1 课件(共23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-08 00:00:00 | ||
图片预览


文档简介
(共23张PPT)
12.3.1等腰三角形的性质
自学目标
1.掌握等腰三角形的性质;
2.能利用等腰三角形的性质解决相关的题目。
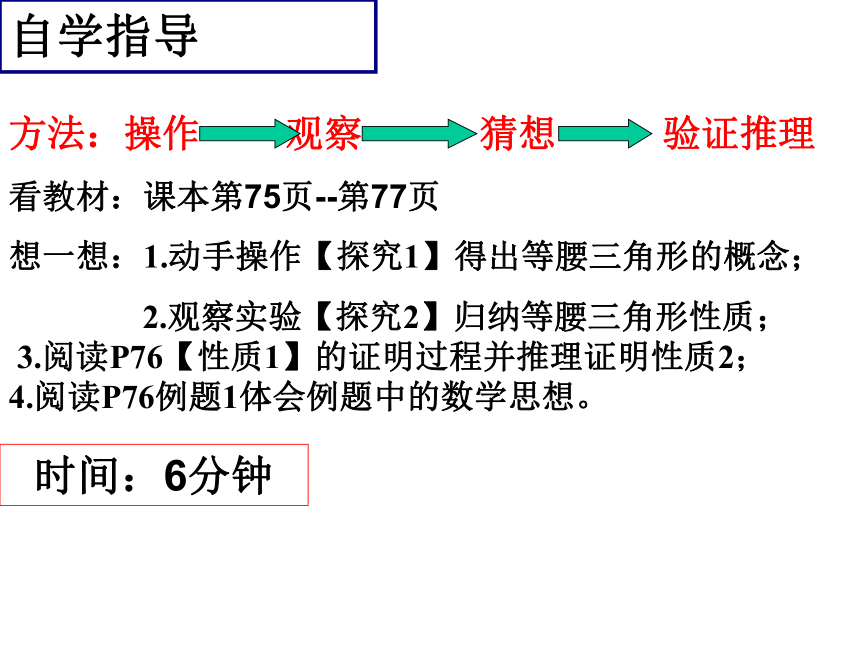
方法:操作 观察 猜想 验证推理
看教材:课本第75页--第77页
想一想:1.动手操作【探究1】得出等腰三角形的概念;
2.观察实验【探究2】归纳等腰三角形性质;
3.阅读P76【性质1】的证明过程并推理证明性质2;
4.阅读P76例题1体会例题中的数学思想。
时间:6分钟
自学指导
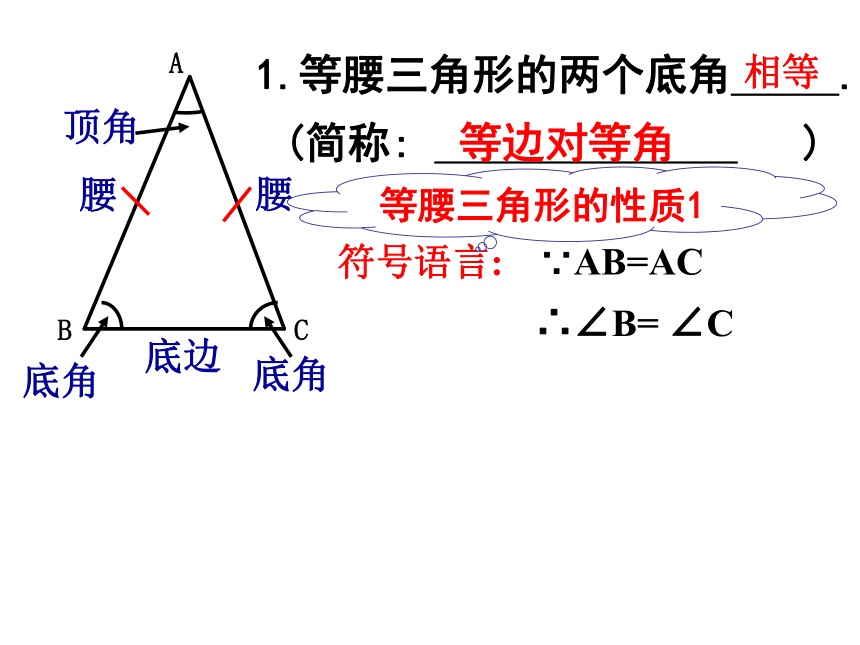
腰
腰
底边
顶角
底角
底角
1.等腰三角形的两个底角 .
∵AB=AC
∴∠B= ∠C
符号语言:
(简称: )
相等
等边对等角
等腰三角形的性质1
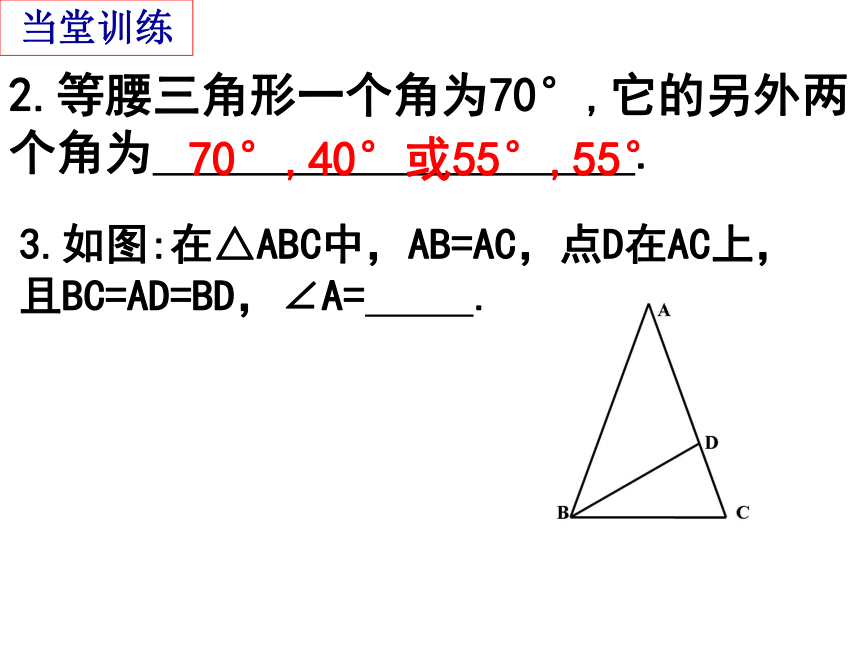
2.等腰三角形一个角为70°,它的另外两
个角为 .
70°,40°或55°,55°
当堂训练
3.如图:在△ABC中,AB=AC,点D在AC上,且BC=AD=BD,∠A= .
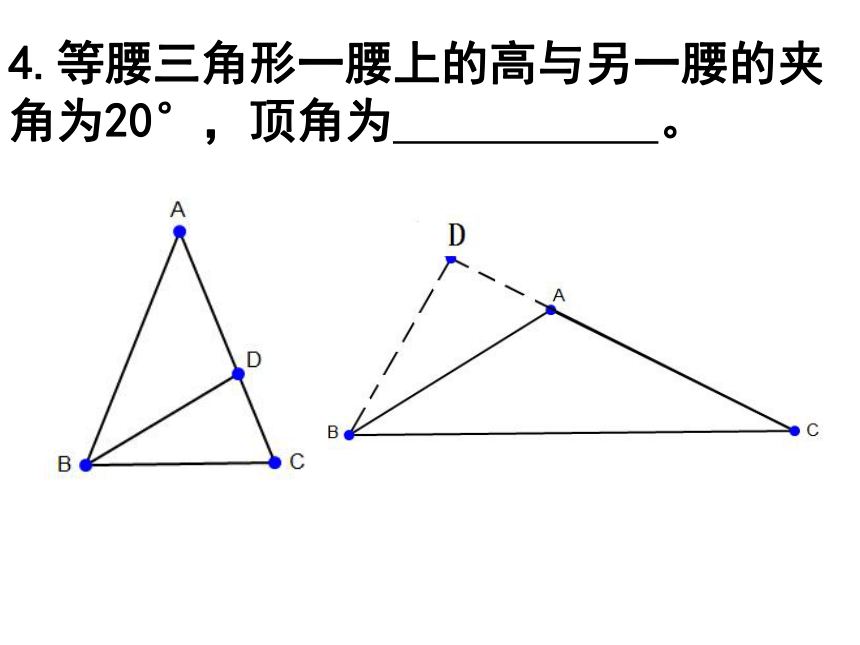
4.等腰三角形一腰上的高与另一腰的夹角为20°,顶角为 。
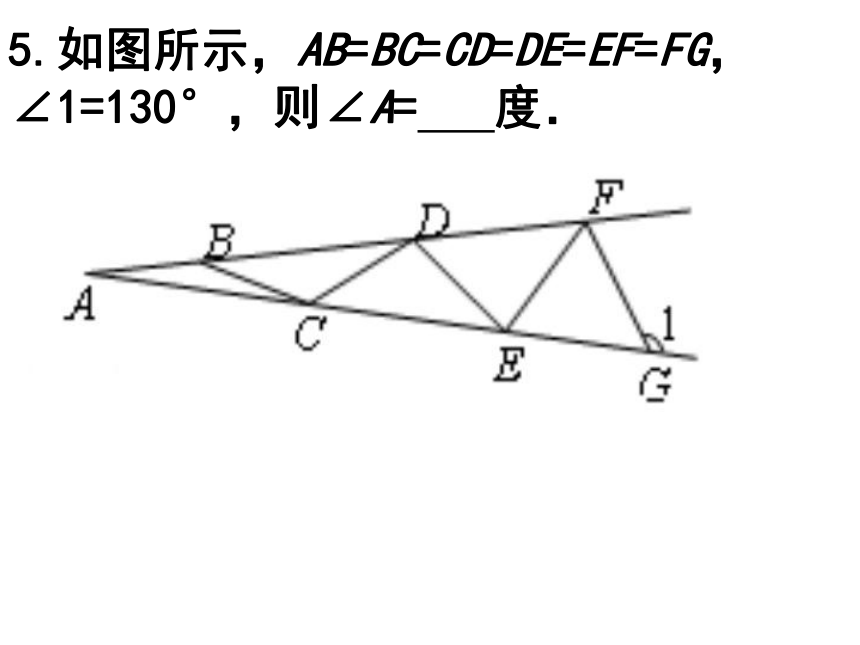
5.如图所示,AB=BC=CD=DE=EF=FG,∠1=130°,则∠A= 度.
效果检测
A
B
C
D
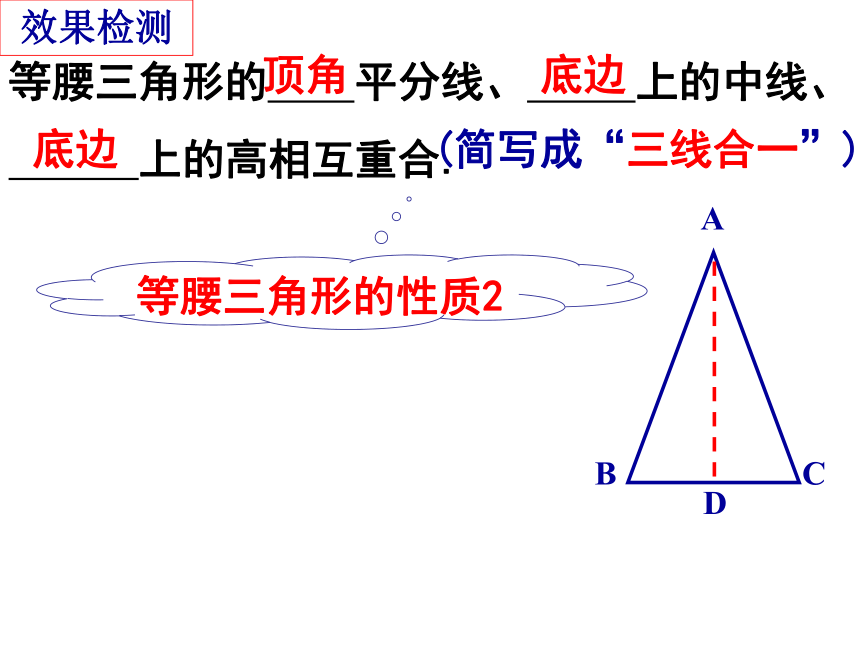
等腰三角形的 平分线、 上的中线、
上的高相互重合.
(简写成“三线合一”).
等腰三角形的性质2
顶角
底边
底边
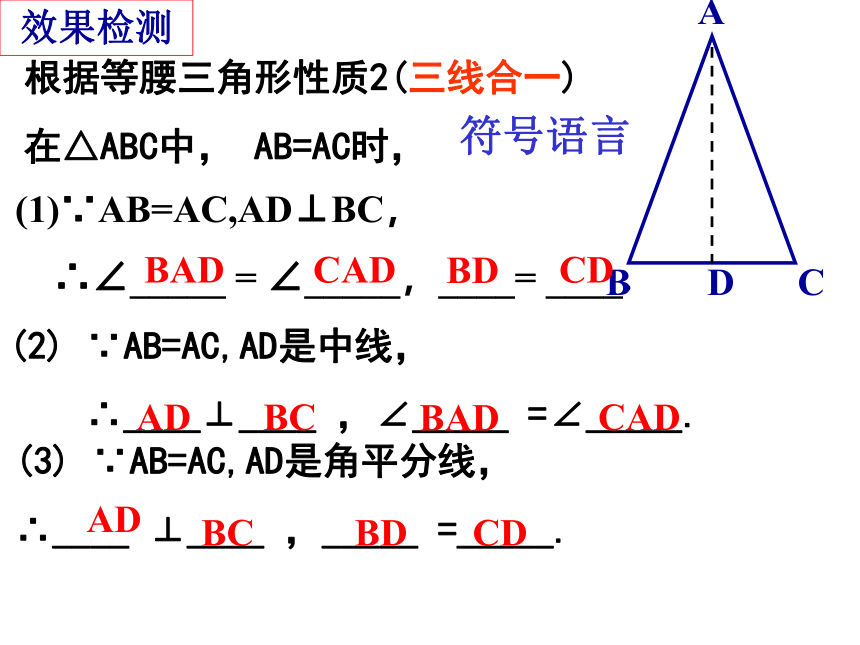
根据等腰三角形性质2(三线合一)
在△ABC中, AB=AC时,
∵AB=AC,AD⊥BC,
∴∠_____ = ∠_____,____= ____.
(2) ∵AB=AC,AD是中线,
∴____⊥____ ,∠_____ =∠_____.
(3) ∵AB=AC,AD是角平分线,
∴____ ⊥____ ,_____ =_____.
A
B
C
D
BAD
CAD
CAD
BD
CD
AD
BC
BD
BAD
BC
CD
符号语言
效果检测
AD
腰
2.两角相等的三角形的是 .
∴AB=AC
∵∠B= ∠C
符号语言:
(简称: )
等腰三角形
等角对等边
等腰三角形的判定
1.在△ABC中,AB=AC,BD=CE, ∠DEF=∠B,求证:△DEF是等腰三角形.
2.在△ABC中,AB=AC,DE⊥BC, 求证:AD=AF
3.在平面直角坐标系中,A(1,3),在坐标轴上找一点P,使△AOP是等腰三角形,则这样的P有多少个?
巧用三线合一
1.在四边形ABCD中,E是AD中点,CE=EF, (1)求证:CD∥AB (2)若BE⊥CF,证明:BE平分∠CBF.
全品P32
等腰直角三角形,AB=AC,点D是BC的中点。
∵∠BAC=90°,AB=AC
点D是BC的中点
∴AD=BD=CD
∠B=∠BAD=∠CAD=∠C=45°
1.如图所示的正方形网格中,网格线的交点称为格点.已知A,B是两格点,如果C也是图中的格点,且使得△ABC为等腰三角形,则点C的个数是( )
当堂训练
1.已知:S△ABC=8,∠A=90°,AB=AC,且BE=AF,D为BC的中点.
(1)图①,判断△DEF的形状;并求四边形AEDF面积
(2)如图②,若E,F分别为AB,CA延长线上的点,△DEF是否仍为等腰直角三角形?
等面积证明等腰三角形的性质
1.在△ABC中,GF⊥AB,GE⊥AC 求证:GF+GE=BD
等面积证明等腰三角形的性质
5.等边△ABC,PE⊥AB,PF⊥AC,PD⊥BC AH⊥BC,求证:PE+PF+PD=AH
2. AB=AC,且BE=CF,AD+EC=AB.
(1)求证:△DEF是等腰三角形;
(2)当∠A=40°时,求∠DEF的度数;
(3)△DEF可能是等腰直角三角形吗?
(4)当∠A为多少度,∠EDF+∠EFD=120°.
等腰三角形的性质
等边对等角
三线合一
2、熟练地进行顶角平分线、
底边中线,底边的高之间
的转化.
1、熟练求解等腰三角形中有关角的度数;
《基础小练习》P41-42
当堂作业
课后作业
1.全品P39-40
2.预习课本P77-78并完成P79练习
12.3.1等腰三角形的性质
自学目标
1.掌握等腰三角形的性质;
2.能利用等腰三角形的性质解决相关的题目。
方法:操作 观察 猜想 验证推理
看教材:课本第75页--第77页
想一想:1.动手操作【探究1】得出等腰三角形的概念;
2.观察实验【探究2】归纳等腰三角形性质;
3.阅读P76【性质1】的证明过程并推理证明性质2;
4.阅读P76例题1体会例题中的数学思想。
时间:6分钟
自学指导
腰
腰
底边
顶角
底角
底角
1.等腰三角形的两个底角 .
∵AB=AC
∴∠B= ∠C
符号语言:
(简称: )
相等
等边对等角
等腰三角形的性质1
2.等腰三角形一个角为70°,它的另外两
个角为 .
70°,40°或55°,55°
当堂训练
3.如图:在△ABC中,AB=AC,点D在AC上,且BC=AD=BD,∠A= .
4.等腰三角形一腰上的高与另一腰的夹角为20°,顶角为 。
5.如图所示,AB=BC=CD=DE=EF=FG,∠1=130°,则∠A= 度.
效果检测
A
B
C
D
等腰三角形的 平分线、 上的中线、
上的高相互重合.
(简写成“三线合一”).
等腰三角形的性质2
顶角
底边
底边
根据等腰三角形性质2(三线合一)
在△ABC中, AB=AC时,
∵AB=AC,AD⊥BC,
∴∠_____ = ∠_____,____= ____.
(2) ∵AB=AC,AD是中线,
∴____⊥____ ,∠_____ =∠_____.
(3) ∵AB=AC,AD是角平分线,
∴____ ⊥____ ,_____ =_____.
A
B
C
D
BAD
CAD
CAD
BD
CD
AD
BC
BD
BAD
BC
CD
符号语言
效果检测
AD
腰
2.两角相等的三角形的是 .
∴AB=AC
∵∠B= ∠C
符号语言:
(简称: )
等腰三角形
等角对等边
等腰三角形的判定
1.在△ABC中,AB=AC,BD=CE, ∠DEF=∠B,求证:△DEF是等腰三角形.
2.在△ABC中,AB=AC,DE⊥BC, 求证:AD=AF
3.在平面直角坐标系中,A(1,3),在坐标轴上找一点P,使△AOP是等腰三角形,则这样的P有多少个?
巧用三线合一
1.在四边形ABCD中,E是AD中点,CE=EF, (1)求证:CD∥AB (2)若BE⊥CF,证明:BE平分∠CBF.
全品P32
等腰直角三角形,AB=AC,点D是BC的中点。
∵∠BAC=90°,AB=AC
点D是BC的中点
∴AD=BD=CD
∠B=∠BAD=∠CAD=∠C=45°
1.如图所示的正方形网格中,网格线的交点称为格点.已知A,B是两格点,如果C也是图中的格点,且使得△ABC为等腰三角形,则点C的个数是( )
当堂训练
1.已知:S△ABC=8,∠A=90°,AB=AC,且BE=AF,D为BC的中点.
(1)图①,判断△DEF的形状;并求四边形AEDF面积
(2)如图②,若E,F分别为AB,CA延长线上的点,△DEF是否仍为等腰直角三角形?
等面积证明等腰三角形的性质
1.在△ABC中,GF⊥AB,GE⊥AC 求证:GF+GE=BD
等面积证明等腰三角形的性质
5.等边△ABC,PE⊥AB,PF⊥AC,PD⊥BC AH⊥BC,求证:PE+PF+PD=AH
2. AB=AC,且BE=CF,AD+EC=AB.
(1)求证:△DEF是等腰三角形;
(2)当∠A=40°时,求∠DEF的度数;
(3)△DEF可能是等腰直角三角形吗?
(4)当∠A为多少度,∠EDF+∠EFD=120°.
等腰三角形的性质
等边对等角
三线合一
2、熟练地进行顶角平分线、
底边中线,底边的高之间
的转化.
1、熟练求解等腰三角形中有关角的度数;
《基础小练习》P41-42
当堂作业
课后作业
1.全品P39-40
2.预习课本P77-78并完成P79练习
