24.1.1 圆[上学期]
文档属性
| 名称 | 24.1.1 圆[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 342.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-10-21 00:00:00 | ||
图片预览






文档简介
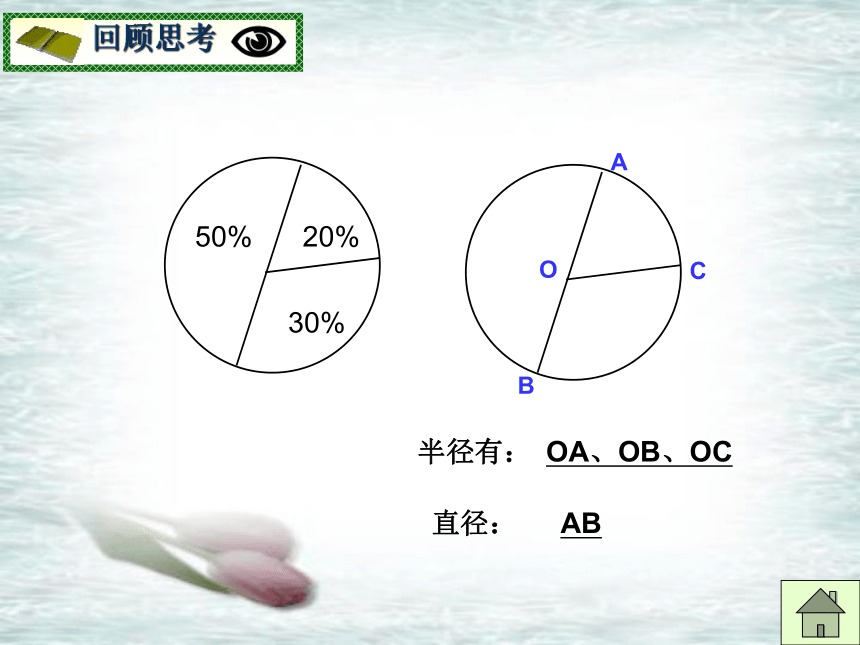
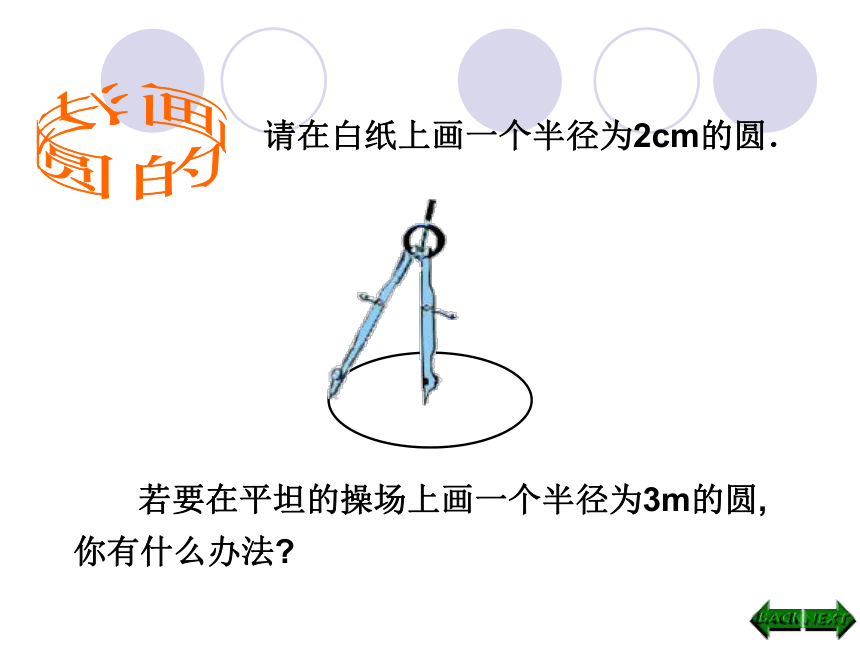
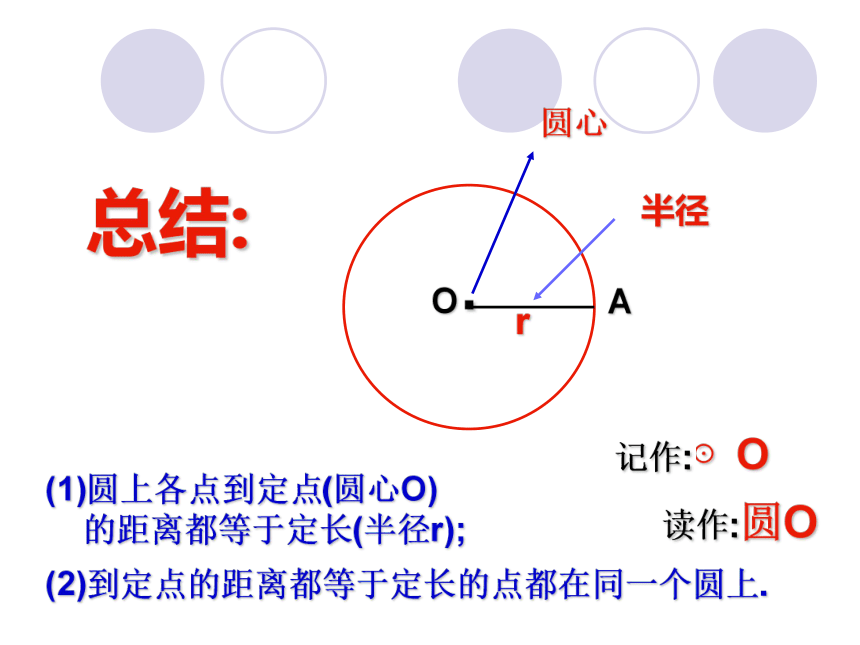
课件25张PPT。第24章 圆一、 创设情境 引入新课圆的世界24.1 圆一石激起千层浪乐在其中一、 创设情境 引入新课圆的世界奥运五环福建土楼一、 创设情境 引入新课圆的世界祥 子小憩片刻一、 创设情境 引入新课圆的世界50%20%30%OACB半径有:OA、OB、OC直径:AB圆的画法请在白纸上画一个半径为2cm的圆. 若要在平坦的操场上画一个半径为3m的圆,你有什么办法? 线段OP绕它固定的一个端点O旋转一周,另一端点P所经过的封闭曲线叫做圆。封闭曲线定点O叫做圆心。线段OP叫做圆的半径。在同一平面内,圆的定义:.OA圆心半径r记作:⊙O读作:圆O总结:(1)圆上各点到定点(圆心O)
的距离都等于定长(半径r);(2)到定点的距离都等于定长的点都在同一个圆上.OA圆的另一定义:r圆心为O、半径为r的圆可以看成
是所有到定点O的距离等于定长
r的点组成的图形。注意:(1)圆心和半径是构成圆的两个重要元素,
圆心确定圆的位置,半径确定圆的大小,
只有当给出圆心和半径这两个要素之后,
才能够确定一个圆。(2)圆是指“圆周”,是曲线,而不是“圆面”。(3)同一个圆的半径处处相等。 车轮为什么做成圆形?探 求 新 知把车轮做成圆形,车轮上各点到车轮中心(圆心)
的距离都等于车轮的半径,
当车轮在平面上滚动时,
车轮中心与平面的距离
保持不变。因此,
当车辆在平坦的路上行驶时,
坐车的人会感觉到非常平稳,
这也是车轮都做成圆形的
数学道理。结论:.OABC弦连接圆上任意两点的线段(图中的线段AB、AC)。直径经过圆心的弦(图中的AB)。弦直径注意:凡直径都是弦,是圆中最长的弦
但弦不一定是直径.即时考你(训案).OADQCBPHGFE如图(1)直径是_______;
(2)弦是_____________;
(3) PQ是直径吗?______;
(4)线段EF、GH
是弦吗?_______.KABCD、DK、AB不是不是●OBCA 1.如图,半径有:______________OA、OB、OC若∠AOB=60°,
则△AOB是_____三角形. 2.如图,弦有:______________AB、BCAC在圆中有长度不等的弦,等边直径是圆中最长的弦。
例题解析例 ⊙O的半径长为2.5 cm,则此圆的最长的弦的长是多少? 解:由于圆的最长的弦过圆心,所以最长的弦是直径,而直径等于半径的2倍,所以圆的最长的弦长为5cm点悟:
由于圆中最长的弦为直径,而直径等于两倍的半径,所以圆的最长的弦的长为5cm。圆弧:连接圆上任意两点间的部分叫做圆弧,简称弧.以A、B为端点的弧记作 AB ,读作:“圆弧AB”或“弧AB”。注意:大于半圆的弧(用三个点表示,如: 或 ),
叫做优弧;小于半圆的弧叫做劣弧. 如:圆的任意一条直径的两个端点把圆分成两条弧,
每一条弧叫做半圆.●OBCA 1.如图,劣弧有:______________2.优弧有:你知道优弧与劣弧的区别么?判断:半圆是弧,但弧不一定是半圆.( )弦与弧1、请写出图中所有的弦;2、请任选一条弦,写出这条弦所对的弧;基础训练1.过圆上一点可以作圆的最长弦有( )条.
A. 1 B. 2 C. 3 D.无数条
2.一点和⊙O上的最近点距离为4cm,最远距离为10cm,
则这个圆的半径是_ ___ __cm.
3.图中有____条直径,____条非直径的弦,圆中以A为一个
端点的优弧有____条,劣弧有____条.
4.如图, ⊙O中,点A、O、D以及点B、O、C分别在一直线
上,图中弦的条数为_____。
5.CD为⊙O的直径,∠EOD=72°,AE交⊙O于B,
且AB=OC,则∠A=_______.A3、712443第5题24°
6、下列说法①直径是弦;②弦是直径;③半圆是弧;④弧是半圆,正确的是 。(填序号)
7、如图,BC是⊙O的直径,点A、E分别在圆上,则圆中弧的条数为 条。
基础训练8、⊙O的半径是2cm,则它的弦长的取值范围是什么??
9、如图,已知:OA、OB是⊙O的两条半径,C、D分别在OA 、OB上,且AC=BD。求证:AD=BC
基础训练拓展训练 爆破时,导火线燃烧的速度是每秒钟0.9cm,点燃导火索的人需要跑到离爆破点120米以外的安全区域,这个导火索的长度为18cm,那么点导火索的人每秒钟跑6.5米是否安全?请谈谈你的收获作 业见试案
的距离都等于定长(半径r);(2)到定点的距离都等于定长的点都在同一个圆上.OA圆的另一定义:r圆心为O、半径为r的圆可以看成
是所有到定点O的距离等于定长
r的点组成的图形。注意:(1)圆心和半径是构成圆的两个重要元素,
圆心确定圆的位置,半径确定圆的大小,
只有当给出圆心和半径这两个要素之后,
才能够确定一个圆。(2)圆是指“圆周”,是曲线,而不是“圆面”。(3)同一个圆的半径处处相等。 车轮为什么做成圆形?探 求 新 知把车轮做成圆形,车轮上各点到车轮中心(圆心)
的距离都等于车轮的半径,
当车轮在平面上滚动时,
车轮中心与平面的距离
保持不变。因此,
当车辆在平坦的路上行驶时,
坐车的人会感觉到非常平稳,
这也是车轮都做成圆形的
数学道理。结论:.OABC弦连接圆上任意两点的线段(图中的线段AB、AC)。直径经过圆心的弦(图中的AB)。弦直径注意:凡直径都是弦,是圆中最长的弦
但弦不一定是直径.即时考你(训案).OADQCBPHGFE如图(1)直径是_______;
(2)弦是_____________;
(3) PQ是直径吗?______;
(4)线段EF、GH
是弦吗?_______.KABCD、DK、AB不是不是●OBCA 1.如图,半径有:______________OA、OB、OC若∠AOB=60°,
则△AOB是_____三角形. 2.如图,弦有:______________AB、BCAC在圆中有长度不等的弦,等边直径是圆中最长的弦。
例题解析例 ⊙O的半径长为2.5 cm,则此圆的最长的弦的长是多少? 解:由于圆的最长的弦过圆心,所以最长的弦是直径,而直径等于半径的2倍,所以圆的最长的弦长为5cm点悟:
由于圆中最长的弦为直径,而直径等于两倍的半径,所以圆的最长的弦的长为5cm。圆弧:连接圆上任意两点间的部分叫做圆弧,简称弧.以A、B为端点的弧记作 AB ,读作:“圆弧AB”或“弧AB”。注意:大于半圆的弧(用三个点表示,如: 或 ),
叫做优弧;小于半圆的弧叫做劣弧. 如:圆的任意一条直径的两个端点把圆分成两条弧,
每一条弧叫做半圆.●OBCA 1.如图,劣弧有:______________2.优弧有:你知道优弧与劣弧的区别么?判断:半圆是弧,但弧不一定是半圆.( )弦与弧1、请写出图中所有的弦;2、请任选一条弦,写出这条弦所对的弧;基础训练1.过圆上一点可以作圆的最长弦有( )条.
A. 1 B. 2 C. 3 D.无数条
2.一点和⊙O上的最近点距离为4cm,最远距离为10cm,
则这个圆的半径是_ ___ __cm.
3.图中有____条直径,____条非直径的弦,圆中以A为一个
端点的优弧有____条,劣弧有____条.
4.如图, ⊙O中,点A、O、D以及点B、O、C分别在一直线
上,图中弦的条数为_____。
5.CD为⊙O的直径,∠EOD=72°,AE交⊙O于B,
且AB=OC,则∠A=_______.A3、712443第5题24°
6、下列说法①直径是弦;②弦是直径;③半圆是弧;④弧是半圆,正确的是 。(填序号)
7、如图,BC是⊙O的直径,点A、E分别在圆上,则圆中弧的条数为 条。
基础训练8、⊙O的半径是2cm,则它的弦长的取值范围是什么??
9、如图,已知:OA、OB是⊙O的两条半径,C、D分别在OA 、OB上,且AC=BD。求证:AD=BC
基础训练拓展训练 爆破时,导火线燃烧的速度是每秒钟0.9cm,点燃导火索的人需要跑到离爆破点120米以外的安全区域,这个导火索的长度为18cm,那么点导火索的人每秒钟跑6.5米是否安全?请谈谈你的收获作 业见试案
同课章节目录
