人教版七年级数学4.1 几何图形 教案
文档属性
| 名称 | 人教版七年级数学4.1 几何图形 教案 |
|
|
| 格式 | zip | ||
| 文件大小 | 968.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-08 10:03:20 | ||
图片预览


文档简介
单元概述 本章的主要内容是学习几何图形与实物的关系,认识点、线、角,并会表示几何图形.学习线段和角的有关概念、几何性质、大小比较、度量与计算,以及简单的应用.本章几何基本概念和相关知识是进一步学习几何的基础,是将来学习平行线、相交线、三角形、四边形、相似、圆等知识的重要基础,在中考中占有重要的地位.
单元总览
4.1 几何图形
4.1.1 立体图形与平面图形
第1课时 (见学生用书P95)
1.能通过观察实际生活中的物体,抽象出几何图形.
2.能通过观察几何图形想象出实物形状.
3.知道几何图形包含立体图形和平面图形两类,注意立体图形与平面图形的区别与联系.
◎重点:识别平面图形与立体图形.
◎难点:实物与几何图形的相互转化.
从城市宏伟的建筑到乡村简朴的住宅,从四通八达的立交桥到街头巷尾的交通标志,从古老的剪纸艺术到现代的城市雕塑,从自然界形态各异的动物到北京的申奥标志……图形世界是多姿多彩的!我们生活在一个图形世界里,这个图形世界中蕴含着大量的几何图形.从这一章开始,我们来探索几何图形的奥秘.
请学生说说所知道的立体图形,教室里都有哪些图形呢 你们能画出来吗
立体图形
阅读教材本课时的相关内容,回答下列问题.
如图,这是一台冰箱.
(1)从整体上看,它的形状是 长方体 .
(2)它有 6 个面,这些面的形状是 长方形 或 正方形 ;它有 12 条棱,这些棱的形状是 线段 ;它有 8 个顶点.
归纳总结 从实物中抽象出的各种图形统称为 几何图形 .有些几何图形的各部分不都在同一平面内,它们是 立体 图形.
将下列实物图与相应的几何图形用线连起来.
平面图形
1.有些几何图形的各部分都在一个平面内,它们是平面图形.
2.立体图形和平面图形有哪些不同点和相同点 请填写下表.
区别 联系
立体图形 各部分 不都 在同一平面内 立体图形中某些部分是平面图形
平面图形 各部分 都 在同一平面内 用平面图形可以构成立体图形
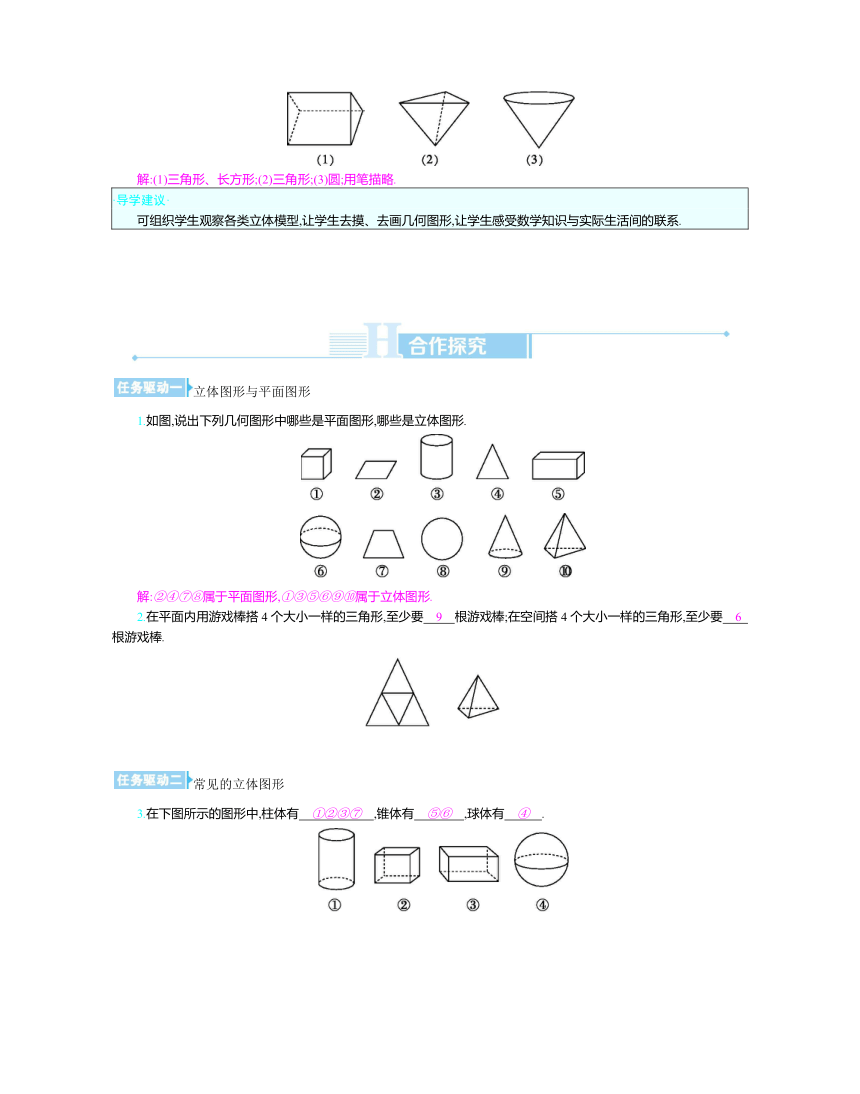
你认为下列立体图形中有哪些平面图形 试着用笔描一描.
解:(1)三角形、长方形;(2)三角形;(3)圆;用笔描略.
·导学建议·
可组织学生观察各类立体模型,让学生去摸、去画几何图形,让学生感受数学知识与实际生活间的联系.
立体图形与平面图形
1.如图,说出下列几何图形中哪些是平面图形,哪些是立体图形.
解:②④⑦⑧属于平面图形,①③⑤⑥⑨⑩属于立体图形.
2.在平面内用游戏棒搭4个大小一样的三角形,至少要 9 根游戏棒;在空间搭4个大小一样的三角形,至少要 6 根游戏棒.
常见的立体图形
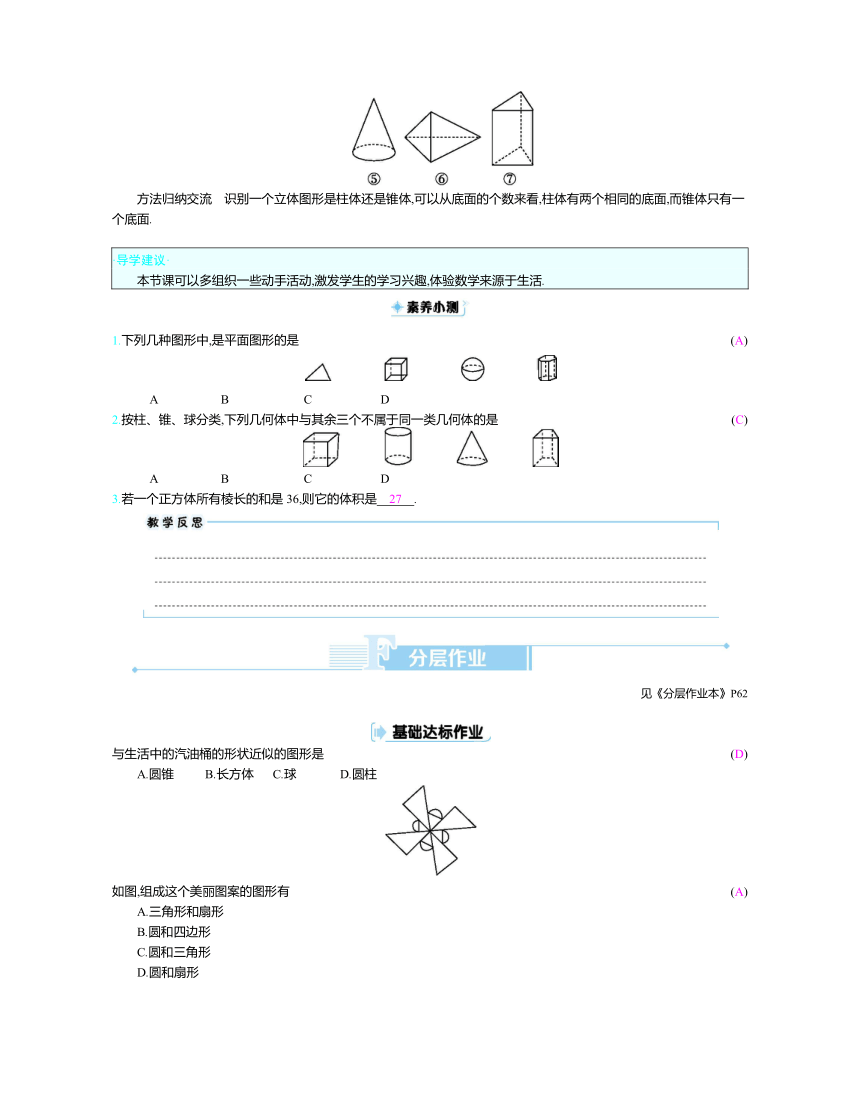
3.在下图所示的图形中,柱体有 ①②③⑦ ,锥体有 ⑤⑥ ,球体有 ④ .
方法归纳交流 识别一个立体图形是柱体还是锥体,可以从底面的个数来看,柱体有两个相同的底面,而锥体只有一个底面.
·导学建议·
本节课可以多组织一些动手活动,激发学生的学习兴趣,体验数学来源于生活.
1.下列几种图形中,是平面图形的是 (A)
A B C D
2.按柱、锥、球分类,下列几何体中与其余三个不属于同一类几何体的是 (C)
A B C D
3.若一个正方体所有棱长的和是36,则它的体积是 27 .
见《分层作业本》P62
与生活中的汽油桶的形状近似的图形是 (D)
A.圆锥 B.长方体 C.球 D.圆柱
如图,组成这个美丽图案的图形有 (A)
A.三角形和扇形
B.圆和四边形
C.圆和三角形
D.圆和扇形
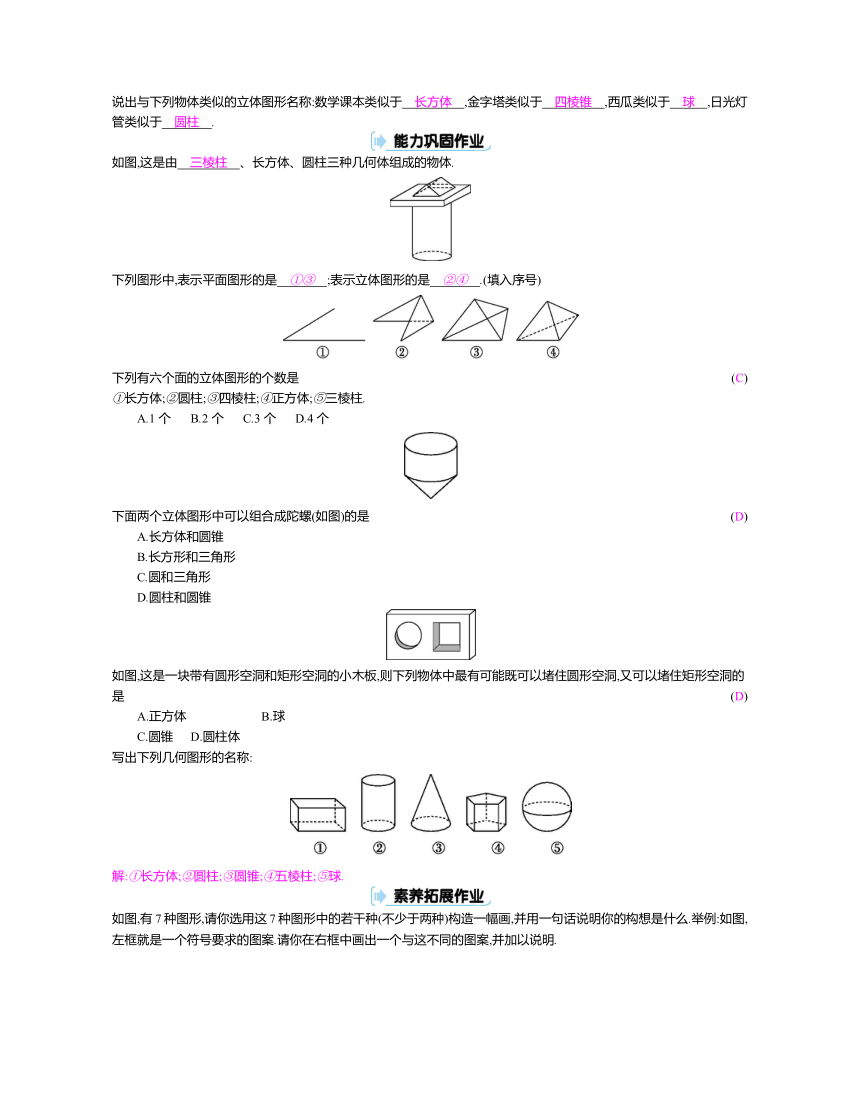
说出与下列物体类似的立体图形名称:数学课本类似于 长方体 ,金字塔类似于 四棱锥 ,西瓜类似于 球 ,日光灯管类似于 圆柱 .
如图,这是由 三棱柱 、长方体、圆柱三种几何体组成的物体.
下列图形中,表示平面图形的是 ①③ ;表示立体图形的是 ②④ .(填入序号)
下列有六个面的立体图形的个数是 (C)
①长方体;②圆柱;③四棱柱;④正方体;⑤三棱柱.
A.1个 B.2个 C.3个 D.4个
下面两个立体图形中可以组合成陀螺(如图)的是 (D)
A.长方体和圆锥
B.长方形和三角形
C.圆和三角形
D.圆柱和圆锥
如图,这是一块带有圆形空洞和矩形空洞的小木板,则下列物体中最有可能既可以堵住圆形空洞,又可以堵住矩形空洞的是 (D)
A.正方体 B.球
C.圆锥 D.圆柱体
写出下列几何图形的名称:
解:①长方体;②圆柱;③圆锥;④五棱柱;⑤球.
如图,有7种图形,请你选用这7种图形中的若干种(不少于两种)构造一幅画,并用一句话说明你的构想是什么.举例:如图,左框就是一个符号要求的图案.请你在右框中画出一个与这不同的图案,并加以说明.
解:
提示:只要设计合理,富有想象力即可.
请你将生活中的物体和它们类似的几何体对应起来.(填序号即可)
解:a—3;b—7;c—4;d—5;e—2;f—1;g—6.
观察下面两行图形,第一行的图形中围绕虚线旋转一周便能与第二行的某个几何体相符合,请动手转一转,连一连.
解:a—2;b—3;c—1.
第2课时 (见学生用书P97)
1.能画出从不同方向看一些基本几何体的示意图,能从不同方向辨认物体的形状.
2.认识简单的立体图形的展开图,能通过展开图想象立体图形.
3.通过从三个方向观察物体及其展开图进一步认识立体图形.
◎重点:从不同的方向看立体图形,立体图形的展开图.
◎难点:通过从三个方向看到的平面图形还原立体图形,通过展开图想象立体图形.
有一首绝句《题西林壁》,其内容是:横看成岭侧成峰,远近高低各不同.不识庐山真面目,只缘身在此山中.
看庐山时,横看、侧看得到的结果不一样.可见看物体不要片面,不能如盲人摸象一般,而应从不同角度去看、去理解,这样得出的结论比片面之词更客观,更有说服力.
从三个方向看立体图形
阅读教材本课时第一个“探究”及其前面的内容,回答下列问题.
填表:
立体图形 从正面看 从左面看 从上面看
圆锥 三角形 三角形 带圆心的圆
正方体 正方形 正方形 正方形
球 圆 圆 圆
立体图形的平面展开图
阅读教材本课时第二个“探究”及其前面的内容,回答下列问题.
“探究”中都是哪些图形的展开图 尝试着用手折一折.
正方体,圆柱,三棱柱,圆锥,长方体.
根据下列立体图形的展开图,填写立体图形的名称.
(1) 长方体 ; (2) 三棱柱 ;(3) 三棱锥 .
·导学建议·
教学中可用几何画板或者动画演示将平面图形折叠又展开的过程.
从三个方向看立体图形
1.如图,该立体图形由三个小正方体组成,请分别画出从它的正面、左面、上面三个方向看所得到的图形.
如图所示:
2.思考:从不同方向看立体图形,会得到相应的 平面图形 .
3.从正面、左面、上面三个方向看一个立体图形,一定会得到三个不同的平面图形吗 请举例说明.
不一定,如从三个方向看球得到的平面图形都是圆.
变式演练 如图,一个斜插吸管的盒装饮料从正面看的图形是 (A)
A B C D
立体图形的平面展开图
4.将一个正方体包装盒剪开铺平,你的小组能得到多少种不同的平面图形 全班共得到多少种不同的平面图形 请将这些平面图形按照所属类型画在下面.
(1)最多四个正方形连成一排.
如图所示:
(2)最多三个正方形连成一排.
如图所示:
(3)最多两个正方形连成一排.
如图所示:
5.思考:下图所示的“田”字形与“凹”字形能不能折叠成正方体 为什么
不能;原因略.
方法归纳交流 在正方体的表面展开图中,每一个顶点至多有3个邻面,所以不存在“田”“凹”“凸”形排列.
变式演练 某正方体有如图所示的三种不同的放置方式,问下底面的数字各是几
解:2,5,1.
·导学建议·
教学中可组织一些活动,让学生通过剪纸、折纸的过程,体会展开图的展开与折叠,并从三个不同方向观察折叠好的立体图形.
1.下列四个几何体中,从正面看和从上面看都是圆的是 (D)
A B C D
2.如图,该几何体从上面看到的形状图是 (D)
A B C D
3.如图,这是一个由5个小正方体和1个圆锥组成的立体图形,从正面看的图形是 (C)
A B C D
4.如图,在以下四个图中,有一个是三棱柱纸盒的展开图,那么这个展开图是 (D)
A B C D
5.将如图所示的图形剪去一个小正方形,使余下的部分恰好能折成一个正方体,下列编号为1、2、3、6的小正方形中不能剪去的是 3 (填编号).
见《分层作业本》P64
如图,这是由四个相同的小正方体组成的立体图形,从上面看到的图形是 (C)
A B C D
下列立体图形中,侧面展开图是扇形的是 (B)
A B C D
下列形状的四张纸板,按图中的线经过折叠可以围成一个三棱柱的是 (C)
A B C D
将一个正方体沿某些棱展开后,能够得到的平面图形是 (C)
A B C D
如图,桌子上放着一个茶壶,小明、小强、小红、小婷四位同学从各自的方向进行观察,那么小强看到的是 (B)
如图,这是一个四棱锥,从上往下看能看到的图形是 (D)
A B C D
用棱长为1的小立方体摆成如图所示的几何体,从左面看这个几何体得到的平面图形的面积是 (B)
A.3 B.4 C.5 D.6
下列选项中可以折叠成如图所示的正方体的是 (A)
A B C D
如图,图①、②、③是图④表示的几何体从三个方向看到的图形,其中①是从 正面 ,图②是从 左面 ,图③是从 上面 .(写出视图名称)
如图,在无阴影的方格中选出两个画出阴影,使它们与图中四个有阴影的正方形一起构成正方体的表面展开图.
解:答案不唯一,如图所示.
图①是一个水平放置的小正方体木块,图②、③是由这样的小正方体木块叠放而成.按照这样的规律继续叠放下去,至第七个叠放的图形时,小正方体木块的总数应是 (C)
A.25 B.66 C.91 D.120
如图,如果约定用字母S表示正方体的侧面,用T表示其上面,B表示其底面.请把相应的字母配在已知加上某些面的记号的正方体的展开图中.
解:如图所示:
用小立方体搭成一个几何体,从正面和左面看到该几何体的平面图如图所示,搭建这样的几何体最多要几个小立方体 最少要几个小立方体 并画出最多和最少时从上面看到的平面图.
解:这样的几何体不只有一种,它最多需要2×4+5=13个小正方体,
它最少需要2+1+2+2+1=8个小正方体.
从上面看:
一个几何体由几个大小相同的小立方体搭成,从上面观察这个几何体,看到的形状如图所示,其中小正方形中的数字表示在该位置的小立方体的个数,请分别画出从正面、左面看到的这个几何体的平面图.
解:如图所示:
4.1.2 点、线、面、体
(见学生用书P99)
1.明确构成几何图形的要素:点、线、面、体.
2.通过探究点、线、面、体之间的关系,培养学生从数学的角度观察事物、分析现象、猜想规律和验证结论的习惯和能力.
3.通过观察平面围绕直线旋转,探究立体图形的形成过程,发展空间想象能力.
◎重点:点、线、面、体之间的关系.
◎难点:点动成线、线动成面、面动成体.
我们生活在一个立体的空间中,在我们的周围,有许多的点、直线、曲线、平面、曲面、立体的事物.
夜空中,繁星点点,坠落的流星划过一道漂亮的弧线.粉笔尖在黑板上运动,形成的图形是线;将粉笔整个横过来,在黑板上一抹,则形成了一个面.
以上种种都与我们本节课所要学的点、线、面、体有莫大关联,这也正体现了数学知识来源于生活.
点、线、面、体的概念
阅读教材本课时的相关内容,回答下列问题.
1.包围着几何体的是 面 ,面与面相交的地方形成 线 ,线与线相交的地方形成 点 .
2.面有 平面 和 曲面 两种,线有 直线 和 曲线 两种.
1.下列现象中,能说明“线动成面”的是 (B)
A.天空划过一道流星
B.汽车雨刷在挡风玻璃上刷出的痕迹
C.抛出一块小石子,石子在空中飞行的路线
D.旋转一扇门,门在空中运动的痕迹
2.如图,圆锥有 两 个面,其中有 1 个是平面, 1 个是曲面,面与面相交有 1 条公共线,且是 曲 线.
3.点、线、面运动的轨迹可以总结为一句话:点动成 线 ,线动成 面 ,面动成 体 .
·导学建议·
学生由于缺乏生活经验,一些生活中的场景并没有见过,可利用多媒体展示给学生.
·学习小助手·
几何体都是由点、线、面、体组成的,点是构成图形的基本元素,点、线、面、体经过运动变化,就能组合成各种各样的几何图形,形成多姿多彩的图形世界.
平面图形的旋转
如图,将直角三角形绕着它的一条直角边旋转一周,就这个旋转过程,请回答下列问题.
(1)直角三角形最左边的顶点,经运动形成了一个怎样的图形
(2)直角三角形水平的边,经运动形成了一个怎样的图形
(3)直角三角形的面经运动形成了一个怎样的图形
解:(1)直角三角形最左边的顶点旋转一周后,形成一个圆,是一条曲线.
(2)直角三角形水平的边旋转一周后,形成一个圆面.
(3)直角三角形的面旋转一周后,形成一个圆锥体.
变式演练 如图,第二行的图形绕虚线旋转一周,便能形成第一行的某个几何体,请把相对应的图形和几何体用线连起来.
解:连接后的图形如下:
·导学建议·
一枚一元硬币(厚度忽略不计)旋转以后,形成一个球体,可以直接在课堂上做实验,让学生通过动手操作,体会生活中点、线、面的运动.
1.下列的立体图形中,有4个面的是 (A)
A.三棱锥 B.三棱柱 C.四棱锥 D.四棱柱
2.笔尖在纸上快速滑动写出一个又一个字,可以说明 (A)
A.点动成线 B.线动成面
C.面动成体 D.不能说明什么问题
3.如图,下列花瓶中,表面可以看作由所给的平面图形绕虚线旋转一周形成的是(D)
A B C D
4.如图,这是一个长为4 cm,宽为3 cm的长方形纸片.
(1)若将此长方形纸片绕长边或短边所在直线旋转一周,能形成的几何体是 ,这能说明的事实是 .
(2)当此长方形纸片绕长边所在直线旋转一周时(如图2),所形成的几何体的体积是多少
(3)当此长方形纸片绕短边所在直线旋转一周时(如图3),所形成的几何体的体积是多少
解:(1)圆柱,面动成体.
(2)绕长边旋转得到的圆柱的底面半径为3 cm,高为4 cm,体积=π×32×4=36π cm3.
(3)绕短边旋转得到的圆柱底面半径为4 cm,高为3 cm,体积=π×42×3=48π cm3.
见《分层作业本》P66
在下列立体图形中,有5个面的是 (A)
A.四棱锥 B.五棱锥
C.四棱柱 D.五棱柱
在下列几何体中,不完全由平面围成的几何体是 (D)
A B C D
如图,左边的图形绕虚线旋转一周形成的图形是 (D)
A B C D
底面是n边形的棱柱共有 (C)
A.n个面 B.(n-1)个面
C.(n+2)个面 D.(n-2)个面
一个长为6 cm,宽为4 cm的长方形绕其一条边旋转一周所形成的几何体的体积是多少
解:当绕长边旋转时,V=π×42×6=96π(cm3);
当绕短边旋转时,V=π×62×4=144π(cm3).
如图,这是一个正七棱柱,它的底面边长都是2 cm,侧棱长是5 cm,观察这个棱柱,回答下列问题.
(1)这个七棱柱共有多少个面 它们分别是什么形状的 哪些面的形状、面积完全相同 侧面的面积是多少 由此你可以猜想得出n棱柱有多少个面
(2)这个七棱柱一共有多少条棱 它们的长度分别是多少
(3)这个七棱柱一共有多少个顶点
(4)通过对棱柱的观察,你能说出n棱柱的顶点数与n的关系及棱的条数与n的关系吗
解:(1)七棱柱有7个侧面,2个底面,共有9个面;上、下两个底面是七边形,侧面是长方形;上、下两个底面的形状相同,面积相等,七个侧面的形状相同,面积相等.要求侧面的面积只需求出一个长方形的面积,再乘7即可,故侧面的面积为2×5×7=70 cm2.
通过上面的分析可知,n棱柱有(n+2)个面.
(2)七棱柱一共有21条棱,它的侧棱长都为5 cm,其余棱长为2 cm.
(3)七棱柱一共有14个顶点.
(4)n棱柱有2n个顶点,有3n条棱.
单元总览
4.1 几何图形
4.1.1 立体图形与平面图形
第1课时 (见学生用书P95)
1.能通过观察实际生活中的物体,抽象出几何图形.
2.能通过观察几何图形想象出实物形状.
3.知道几何图形包含立体图形和平面图形两类,注意立体图形与平面图形的区别与联系.
◎重点:识别平面图形与立体图形.
◎难点:实物与几何图形的相互转化.
从城市宏伟的建筑到乡村简朴的住宅,从四通八达的立交桥到街头巷尾的交通标志,从古老的剪纸艺术到现代的城市雕塑,从自然界形态各异的动物到北京的申奥标志……图形世界是多姿多彩的!我们生活在一个图形世界里,这个图形世界中蕴含着大量的几何图形.从这一章开始,我们来探索几何图形的奥秘.
请学生说说所知道的立体图形,教室里都有哪些图形呢 你们能画出来吗
立体图形
阅读教材本课时的相关内容,回答下列问题.
如图,这是一台冰箱.
(1)从整体上看,它的形状是 长方体 .
(2)它有 6 个面,这些面的形状是 长方形 或 正方形 ;它有 12 条棱,这些棱的形状是 线段 ;它有 8 个顶点.
归纳总结 从实物中抽象出的各种图形统称为 几何图形 .有些几何图形的各部分不都在同一平面内,它们是 立体 图形.
将下列实物图与相应的几何图形用线连起来.
平面图形
1.有些几何图形的各部分都在一个平面内,它们是平面图形.
2.立体图形和平面图形有哪些不同点和相同点 请填写下表.
区别 联系
立体图形 各部分 不都 在同一平面内 立体图形中某些部分是平面图形
平面图形 各部分 都 在同一平面内 用平面图形可以构成立体图形
你认为下列立体图形中有哪些平面图形 试着用笔描一描.
解:(1)三角形、长方形;(2)三角形;(3)圆;用笔描略.
·导学建议·
可组织学生观察各类立体模型,让学生去摸、去画几何图形,让学生感受数学知识与实际生活间的联系.
立体图形与平面图形
1.如图,说出下列几何图形中哪些是平面图形,哪些是立体图形.
解:②④⑦⑧属于平面图形,①③⑤⑥⑨⑩属于立体图形.
2.在平面内用游戏棒搭4个大小一样的三角形,至少要 9 根游戏棒;在空间搭4个大小一样的三角形,至少要 6 根游戏棒.
常见的立体图形
3.在下图所示的图形中,柱体有 ①②③⑦ ,锥体有 ⑤⑥ ,球体有 ④ .
方法归纳交流 识别一个立体图形是柱体还是锥体,可以从底面的个数来看,柱体有两个相同的底面,而锥体只有一个底面.
·导学建议·
本节课可以多组织一些动手活动,激发学生的学习兴趣,体验数学来源于生活.
1.下列几种图形中,是平面图形的是 (A)
A B C D
2.按柱、锥、球分类,下列几何体中与其余三个不属于同一类几何体的是 (C)
A B C D
3.若一个正方体所有棱长的和是36,则它的体积是 27 .
见《分层作业本》P62
与生活中的汽油桶的形状近似的图形是 (D)
A.圆锥 B.长方体 C.球 D.圆柱
如图,组成这个美丽图案的图形有 (A)
A.三角形和扇形
B.圆和四边形
C.圆和三角形
D.圆和扇形
说出与下列物体类似的立体图形名称:数学课本类似于 长方体 ,金字塔类似于 四棱锥 ,西瓜类似于 球 ,日光灯管类似于 圆柱 .
如图,这是由 三棱柱 、长方体、圆柱三种几何体组成的物体.
下列图形中,表示平面图形的是 ①③ ;表示立体图形的是 ②④ .(填入序号)
下列有六个面的立体图形的个数是 (C)
①长方体;②圆柱;③四棱柱;④正方体;⑤三棱柱.
A.1个 B.2个 C.3个 D.4个
下面两个立体图形中可以组合成陀螺(如图)的是 (D)
A.长方体和圆锥
B.长方形和三角形
C.圆和三角形
D.圆柱和圆锥
如图,这是一块带有圆形空洞和矩形空洞的小木板,则下列物体中最有可能既可以堵住圆形空洞,又可以堵住矩形空洞的是 (D)
A.正方体 B.球
C.圆锥 D.圆柱体
写出下列几何图形的名称:
解:①长方体;②圆柱;③圆锥;④五棱柱;⑤球.
如图,有7种图形,请你选用这7种图形中的若干种(不少于两种)构造一幅画,并用一句话说明你的构想是什么.举例:如图,左框就是一个符号要求的图案.请你在右框中画出一个与这不同的图案,并加以说明.
解:
提示:只要设计合理,富有想象力即可.
请你将生活中的物体和它们类似的几何体对应起来.(填序号即可)
解:a—3;b—7;c—4;d—5;e—2;f—1;g—6.
观察下面两行图形,第一行的图形中围绕虚线旋转一周便能与第二行的某个几何体相符合,请动手转一转,连一连.
解:a—2;b—3;c—1.
第2课时 (见学生用书P97)
1.能画出从不同方向看一些基本几何体的示意图,能从不同方向辨认物体的形状.
2.认识简单的立体图形的展开图,能通过展开图想象立体图形.
3.通过从三个方向观察物体及其展开图进一步认识立体图形.
◎重点:从不同的方向看立体图形,立体图形的展开图.
◎难点:通过从三个方向看到的平面图形还原立体图形,通过展开图想象立体图形.
有一首绝句《题西林壁》,其内容是:横看成岭侧成峰,远近高低各不同.不识庐山真面目,只缘身在此山中.
看庐山时,横看、侧看得到的结果不一样.可见看物体不要片面,不能如盲人摸象一般,而应从不同角度去看、去理解,这样得出的结论比片面之词更客观,更有说服力.
从三个方向看立体图形
阅读教材本课时第一个“探究”及其前面的内容,回答下列问题.
填表:
立体图形 从正面看 从左面看 从上面看
圆锥 三角形 三角形 带圆心的圆
正方体 正方形 正方形 正方形
球 圆 圆 圆
立体图形的平面展开图
阅读教材本课时第二个“探究”及其前面的内容,回答下列问题.
“探究”中都是哪些图形的展开图 尝试着用手折一折.
正方体,圆柱,三棱柱,圆锥,长方体.
根据下列立体图形的展开图,填写立体图形的名称.
(1) 长方体 ; (2) 三棱柱 ;(3) 三棱锥 .
·导学建议·
教学中可用几何画板或者动画演示将平面图形折叠又展开的过程.
从三个方向看立体图形
1.如图,该立体图形由三个小正方体组成,请分别画出从它的正面、左面、上面三个方向看所得到的图形.
如图所示:
2.思考:从不同方向看立体图形,会得到相应的 平面图形 .
3.从正面、左面、上面三个方向看一个立体图形,一定会得到三个不同的平面图形吗 请举例说明.
不一定,如从三个方向看球得到的平面图形都是圆.
变式演练 如图,一个斜插吸管的盒装饮料从正面看的图形是 (A)
A B C D
立体图形的平面展开图
4.将一个正方体包装盒剪开铺平,你的小组能得到多少种不同的平面图形 全班共得到多少种不同的平面图形 请将这些平面图形按照所属类型画在下面.
(1)最多四个正方形连成一排.
如图所示:
(2)最多三个正方形连成一排.
如图所示:
(3)最多两个正方形连成一排.
如图所示:
5.思考:下图所示的“田”字形与“凹”字形能不能折叠成正方体 为什么
不能;原因略.
方法归纳交流 在正方体的表面展开图中,每一个顶点至多有3个邻面,所以不存在“田”“凹”“凸”形排列.
变式演练 某正方体有如图所示的三种不同的放置方式,问下底面的数字各是几
解:2,5,1.
·导学建议·
教学中可组织一些活动,让学生通过剪纸、折纸的过程,体会展开图的展开与折叠,并从三个不同方向观察折叠好的立体图形.
1.下列四个几何体中,从正面看和从上面看都是圆的是 (D)
A B C D
2.如图,该几何体从上面看到的形状图是 (D)
A B C D
3.如图,这是一个由5个小正方体和1个圆锥组成的立体图形,从正面看的图形是 (C)
A B C D
4.如图,在以下四个图中,有一个是三棱柱纸盒的展开图,那么这个展开图是 (D)
A B C D
5.将如图所示的图形剪去一个小正方形,使余下的部分恰好能折成一个正方体,下列编号为1、2、3、6的小正方形中不能剪去的是 3 (填编号).
见《分层作业本》P64
如图,这是由四个相同的小正方体组成的立体图形,从上面看到的图形是 (C)
A B C D
下列立体图形中,侧面展开图是扇形的是 (B)
A B C D
下列形状的四张纸板,按图中的线经过折叠可以围成一个三棱柱的是 (C)
A B C D
将一个正方体沿某些棱展开后,能够得到的平面图形是 (C)
A B C D
如图,桌子上放着一个茶壶,小明、小强、小红、小婷四位同学从各自的方向进行观察,那么小强看到的是 (B)
如图,这是一个四棱锥,从上往下看能看到的图形是 (D)
A B C D
用棱长为1的小立方体摆成如图所示的几何体,从左面看这个几何体得到的平面图形的面积是 (B)
A.3 B.4 C.5 D.6
下列选项中可以折叠成如图所示的正方体的是 (A)
A B C D
如图,图①、②、③是图④表示的几何体从三个方向看到的图形,其中①是从 正面 ,图②是从 左面 ,图③是从 上面 .(写出视图名称)
如图,在无阴影的方格中选出两个画出阴影,使它们与图中四个有阴影的正方形一起构成正方体的表面展开图.
解:答案不唯一,如图所示.
图①是一个水平放置的小正方体木块,图②、③是由这样的小正方体木块叠放而成.按照这样的规律继续叠放下去,至第七个叠放的图形时,小正方体木块的总数应是 (C)
A.25 B.66 C.91 D.120
如图,如果约定用字母S表示正方体的侧面,用T表示其上面,B表示其底面.请把相应的字母配在已知加上某些面的记号的正方体的展开图中.
解:如图所示:
用小立方体搭成一个几何体,从正面和左面看到该几何体的平面图如图所示,搭建这样的几何体最多要几个小立方体 最少要几个小立方体 并画出最多和最少时从上面看到的平面图.
解:这样的几何体不只有一种,它最多需要2×4+5=13个小正方体,
它最少需要2+1+2+2+1=8个小正方体.
从上面看:
一个几何体由几个大小相同的小立方体搭成,从上面观察这个几何体,看到的形状如图所示,其中小正方形中的数字表示在该位置的小立方体的个数,请分别画出从正面、左面看到的这个几何体的平面图.
解:如图所示:
4.1.2 点、线、面、体
(见学生用书P99)
1.明确构成几何图形的要素:点、线、面、体.
2.通过探究点、线、面、体之间的关系,培养学生从数学的角度观察事物、分析现象、猜想规律和验证结论的习惯和能力.
3.通过观察平面围绕直线旋转,探究立体图形的形成过程,发展空间想象能力.
◎重点:点、线、面、体之间的关系.
◎难点:点动成线、线动成面、面动成体.
我们生活在一个立体的空间中,在我们的周围,有许多的点、直线、曲线、平面、曲面、立体的事物.
夜空中,繁星点点,坠落的流星划过一道漂亮的弧线.粉笔尖在黑板上运动,形成的图形是线;将粉笔整个横过来,在黑板上一抹,则形成了一个面.
以上种种都与我们本节课所要学的点、线、面、体有莫大关联,这也正体现了数学知识来源于生活.
点、线、面、体的概念
阅读教材本课时的相关内容,回答下列问题.
1.包围着几何体的是 面 ,面与面相交的地方形成 线 ,线与线相交的地方形成 点 .
2.面有 平面 和 曲面 两种,线有 直线 和 曲线 两种.
1.下列现象中,能说明“线动成面”的是 (B)
A.天空划过一道流星
B.汽车雨刷在挡风玻璃上刷出的痕迹
C.抛出一块小石子,石子在空中飞行的路线
D.旋转一扇门,门在空中运动的痕迹
2.如图,圆锥有 两 个面,其中有 1 个是平面, 1 个是曲面,面与面相交有 1 条公共线,且是 曲 线.
3.点、线、面运动的轨迹可以总结为一句话:点动成 线 ,线动成 面 ,面动成 体 .
·导学建议·
学生由于缺乏生活经验,一些生活中的场景并没有见过,可利用多媒体展示给学生.
·学习小助手·
几何体都是由点、线、面、体组成的,点是构成图形的基本元素,点、线、面、体经过运动变化,就能组合成各种各样的几何图形,形成多姿多彩的图形世界.
平面图形的旋转
如图,将直角三角形绕着它的一条直角边旋转一周,就这个旋转过程,请回答下列问题.
(1)直角三角形最左边的顶点,经运动形成了一个怎样的图形
(2)直角三角形水平的边,经运动形成了一个怎样的图形
(3)直角三角形的面经运动形成了一个怎样的图形
解:(1)直角三角形最左边的顶点旋转一周后,形成一个圆,是一条曲线.
(2)直角三角形水平的边旋转一周后,形成一个圆面.
(3)直角三角形的面旋转一周后,形成一个圆锥体.
变式演练 如图,第二行的图形绕虚线旋转一周,便能形成第一行的某个几何体,请把相对应的图形和几何体用线连起来.
解:连接后的图形如下:
·导学建议·
一枚一元硬币(厚度忽略不计)旋转以后,形成一个球体,可以直接在课堂上做实验,让学生通过动手操作,体会生活中点、线、面的运动.
1.下列的立体图形中,有4个面的是 (A)
A.三棱锥 B.三棱柱 C.四棱锥 D.四棱柱
2.笔尖在纸上快速滑动写出一个又一个字,可以说明 (A)
A.点动成线 B.线动成面
C.面动成体 D.不能说明什么问题
3.如图,下列花瓶中,表面可以看作由所给的平面图形绕虚线旋转一周形成的是(D)
A B C D
4.如图,这是一个长为4 cm,宽为3 cm的长方形纸片.
(1)若将此长方形纸片绕长边或短边所在直线旋转一周,能形成的几何体是 ,这能说明的事实是 .
(2)当此长方形纸片绕长边所在直线旋转一周时(如图2),所形成的几何体的体积是多少
(3)当此长方形纸片绕短边所在直线旋转一周时(如图3),所形成的几何体的体积是多少
解:(1)圆柱,面动成体.
(2)绕长边旋转得到的圆柱的底面半径为3 cm,高为4 cm,体积=π×32×4=36π cm3.
(3)绕短边旋转得到的圆柱底面半径为4 cm,高为3 cm,体积=π×42×3=48π cm3.
见《分层作业本》P66
在下列立体图形中,有5个面的是 (A)
A.四棱锥 B.五棱锥
C.四棱柱 D.五棱柱
在下列几何体中,不完全由平面围成的几何体是 (D)
A B C D
如图,左边的图形绕虚线旋转一周形成的图形是 (D)
A B C D
底面是n边形的棱柱共有 (C)
A.n个面 B.(n-1)个面
C.(n+2)个面 D.(n-2)个面
一个长为6 cm,宽为4 cm的长方形绕其一条边旋转一周所形成的几何体的体积是多少
解:当绕长边旋转时,V=π×42×6=96π(cm3);
当绕短边旋转时,V=π×62×4=144π(cm3).
如图,这是一个正七棱柱,它的底面边长都是2 cm,侧棱长是5 cm,观察这个棱柱,回答下列问题.
(1)这个七棱柱共有多少个面 它们分别是什么形状的 哪些面的形状、面积完全相同 侧面的面积是多少 由此你可以猜想得出n棱柱有多少个面
(2)这个七棱柱一共有多少条棱 它们的长度分别是多少
(3)这个七棱柱一共有多少个顶点
(4)通过对棱柱的观察,你能说出n棱柱的顶点数与n的关系及棱的条数与n的关系吗
解:(1)七棱柱有7个侧面,2个底面,共有9个面;上、下两个底面是七边形,侧面是长方形;上、下两个底面的形状相同,面积相等,七个侧面的形状相同,面积相等.要求侧面的面积只需求出一个长方形的面积,再乘7即可,故侧面的面积为2×5×7=70 cm2.
通过上面的分析可知,n棱柱有(n+2)个面.
(2)七棱柱一共有21条棱,它的侧棱长都为5 cm,其余棱长为2 cm.
(3)七棱柱一共有14个顶点.
(4)n棱柱有2n个顶点,有3n条棱.
