人教版数学七年级上册4.3.3 余角和补角 学案(含答案)
文档属性
| 名称 | 人教版数学七年级上册4.3.3 余角和补角 学案(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 461.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-08 10:08:00 | ||
图片预览


文档简介
第四章 几何图形初步
4.2 直线、射线、线段
第1课时 直线、射线、线段
学习目标:1. 了解余角、补角的概念,掌握余角和补角的性质,并能利用余角、补角
的知识解决相关问题.
2. 了解方位角的概念,并能用方位角知识解决一些简单的实际问题.
重点:了解余角、补角的概念及性质,了解方位角的概念和表达方式.
难点:运用余角、补角和方位角的相关知识解题.
自主学习
教学备注:学生在课前完成自主学习部分。
一、知识链接
如图①,在长方形中,∠1+∠2= °,
∠3+∠4= °.
图①
二、新知预习
1. 如果两个角的和等于90°(直角),就说这两个角互为______ (简称为两个角______ ).
如图①,可以说∠1是∠2的余角,或∠2是∠1的余角,或∠1和∠2互余.
2. 如果两个角的和等于180°(平角),就说这两个角互为______ (简称为两个角______).
如图①,可以说∠3是∠4的补角,或∠4是∠3的补角,或∠3和∠4互补.
三、自学自测
1. 图中给出的各角,哪些互为余角?
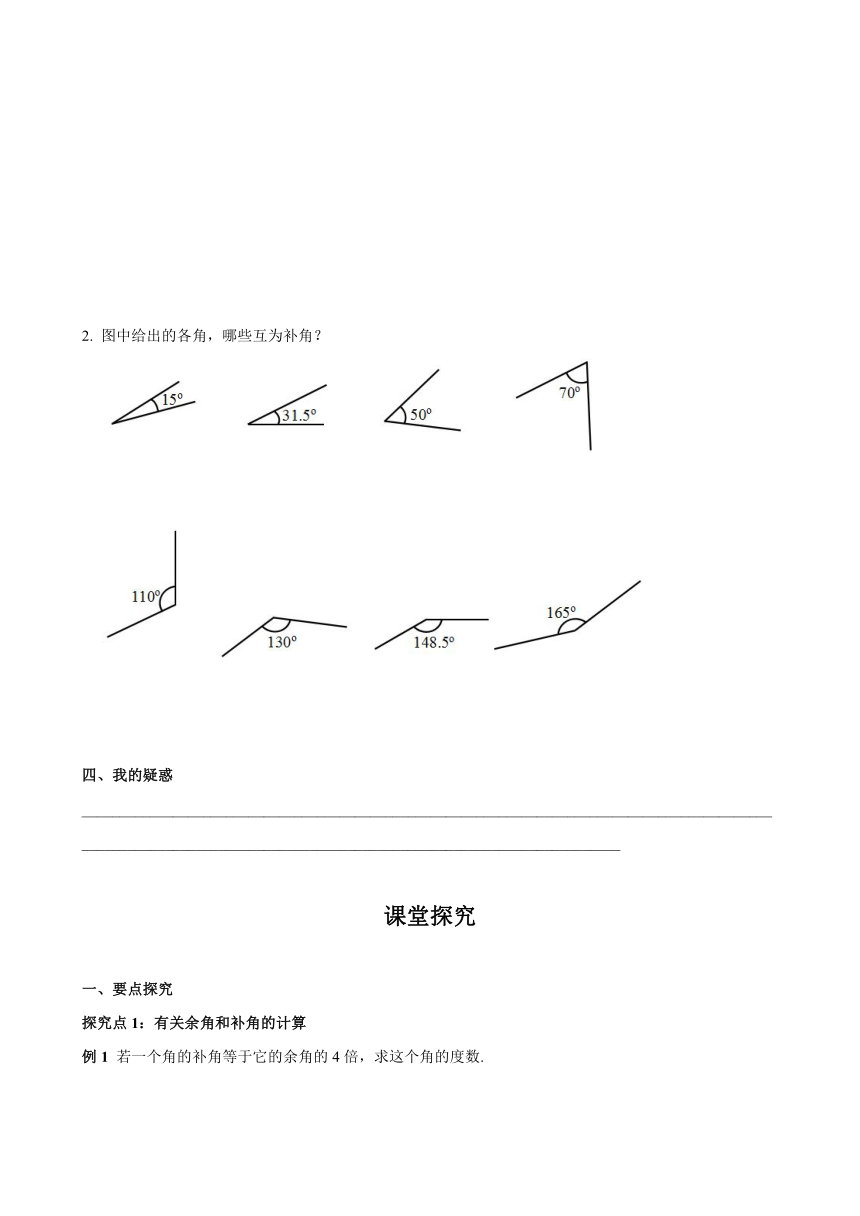
2. 图中给出的各角,哪些互为补角?
四、我的疑惑
__________________________________________________________________________________________________________________________________________________________________
课堂探究
要点探究
探究点1:有关余角和补角的计算
例1 若一个角的补角等于它的余角的4倍,求这个角的度数.
方法总结:余补角问题中,若角之间有比较明显的倍分关系,可尝试将较小的角设为未知数,列方程解答.
例2 如图,已知O为AD上一点,∠AOC与∠AOB互补,OM,ON分别为∠AOC,∠AOB的平分线,若∠MON=40°,试求∠AOC与∠AOB的度数.
观察与思考:
∠α ∠α的余角 ∠α的补角
5°
32°
45°
77°
62°23′
x°(0<x<90)
观察可得结论:
锐角的补角比它的余角大_____.
针对训练
如果∠a=36°,那么∠a的余角等于( )
A.54° B.64° C.144° D.134°
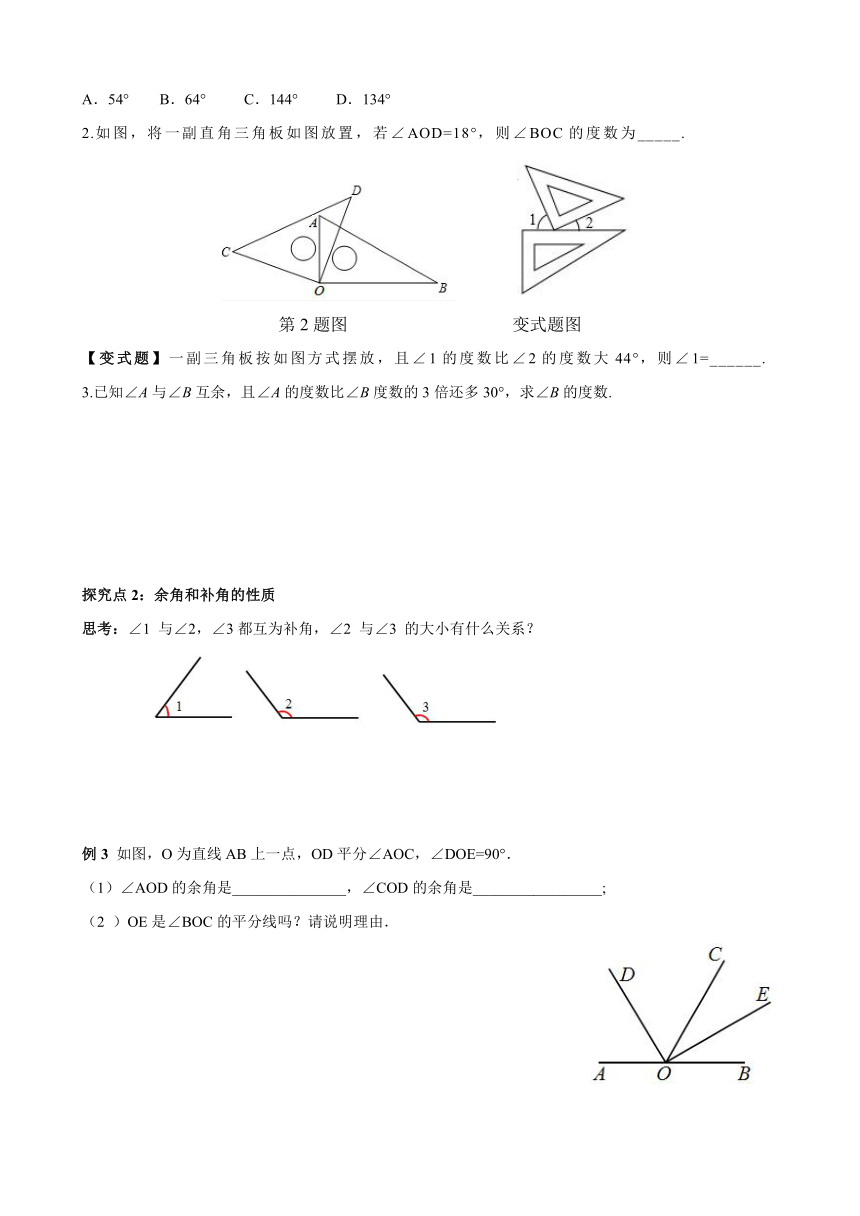
2.如图,将一副直角三角板如图放置,若∠AOD=18°,则∠BOC的度数为_____.
第2题图 变式题图
【变式题】一副三角板按如图方式摆放,且∠1的度数比∠2的度数大44°,则∠1=______.
3.已知∠A与∠B互余,且∠A的度数比∠B度数的3倍还多30°,求∠B的度数.
探究点2:余角和补角的性质
思考:∠1 与∠2,∠3都互为补角,∠2 与∠3 的大小有什么关系?
例3 如图,O为直线AB上一点,OD平分∠AOC,∠DOE=90°.
(1)∠AOD的余角是_______________,∠COD的余角是_________________;
(2 )OE是∠BOC的平分线吗?请说明理由.
针对训练
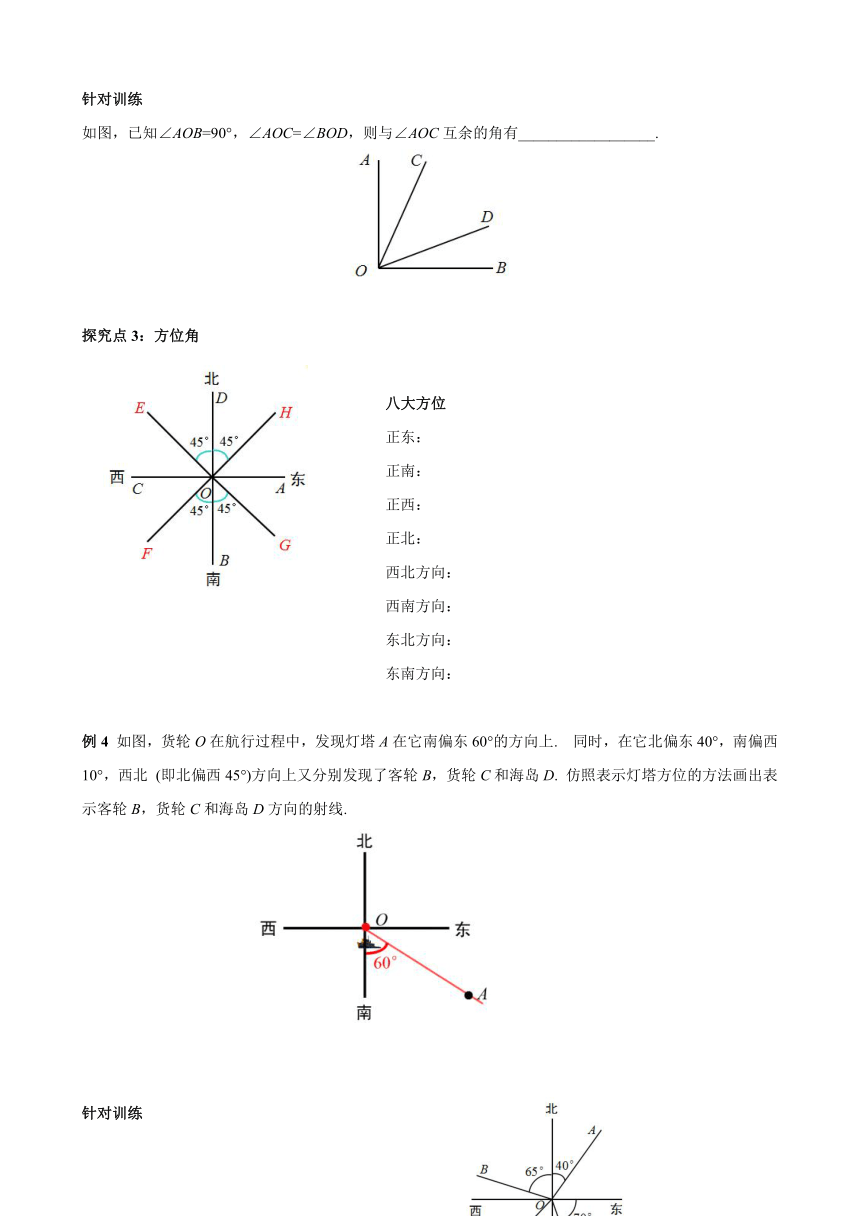
如图,已知∠AOB=90°,∠AOC=∠BOD,则与∠AOC互余的角有__________________.
探究点3:方位角
八大方位
正东:
正南:
正西:
正北:
西北方向:
西南方向:
东北方向:
东南方向:
例4 如图,货轮O在航行过程中,发现灯塔A在它南偏东60°的方向上. 同时,在它北偏东40°,南偏西10°,西北 (即北偏西45°)方向上又分别发现了客轮B,货轮C和海岛D. 仿照表示灯塔方位的方法画出表示客轮B,货轮C和海岛D方向的射线.
针对训练
1. 如图,说出下列方位
(1) 射线 OA 表示的方向为 .
(2) 射线 OB 表示的方向为 .
(3) 射线 OC 表示的方向为 . .
(4) 射线 OD 表示的方向为 .
2.费俊龙、聂海胜乘坐“神舟”六号遨游太空时,我国当时派出远望一号~四号船队,跟踪检测. 其中远望一、二号停在太平洋洋面上,某一时刻,分别测得神舟六号在北偏东60°和北偏东30°的方向,你能在下图中画出当时神舟六号所处的位置吗?
二、课堂小结
当堂检测
1.一个角的余角是它的2倍,这个角的度数是( )
A.30° B.45° C.60° D.75°
2.下列说法正确的是( )
A.一个角的补角一定大于它本身
B.一个角的余角一定小于它本身
C.一个钝角减去一个锐角的差一定是一个锐角
D.一个角的余角一定小于其补角
3.已知∠A与∠B互余,∠B与∠C互补,若∠A=60°,则∠C的度数是_______.
4.∠1与∠2 互余,∠1 = (6x + 8)°,∠2 = (4x-8)°,则∠1= ,∠2= .
5. 如图,已知∠ACB=∠CDB=90°.
图中有哪几对互余的角?
(2) 图中哪几对角是相等的角(直角除外)?为什么?
6 垃圾打捞船A和B都停驻在湖边观测湖面,从A船发现它的北偏东60°方向有白色
漂浮物,同时,从B船也发现该白色漂浮物在它的北偏西30°方向.
(1) 试在图中确定白色漂浮物C的位置;
(2) 点C在点A的北偏东60°的方向上,那么点 A在点C的________方向上.
A. 南偏东30° B. 南偏西30°
C. 南偏东60° D. 南偏西60°
参考答案
自主学习
一、知识链接
90 180
二、新知预习
1.余角 互余 2.补角 互补
三、自学自测
1.10°和80°的角、25°和65°的角、44°和46°的角互为余角.
2.15°和165°的角、31.5°和148.5°的角、50°和130°的角、70°和110°的角互为补角.
课堂探究
一、要点探究
探究点1:
例1 解:设这个角为 x°,则它的补角是 ( 180-x )°,余角是 ( 90-x )° .
根据题意,得180-x = 4 ( 90-x ) .解得x = 60.
答:这个角的度数是60°.
例2 解:设∠AOB=x,因为∠AOC与∠AOB互补,则∠AOC=180°-x.因为OM,ON分别为∠AOC,∠AOB的平分线,所以∠AOM=(180°-x),∠AON=x.所以(180°-x)-x=40°. 解得x=50°,则180°-x=130°.即∠AOB=50°,∠AOC=130°.
观察与思考
90°
【针对训练】
1.A 2.162° 【变式题】67°
3. 解:∵∠A与∠B互余,∴∠A+∠B=90°,又∵∠A的度数比∠B度数的3倍还多30°,
∴∠A=3∠B+30°,∴3∠B+30°+∠B=90°,解得∠B=15°.故∠B的度数为15°.
探究点2:
思考 ∠2=180°-∠1,∠3=180°-∠1,∠2=∠3.
例3 解:(1)∠COE、∠BOE ∠COE、∠BOE
解:是,理由如下:∵∠DOE=90°,∴∠COD+∠COE=90°,∠AOD+∠BOE=90°,∴∠AOD+∠BOE=
∠COD+∠COE,∵OD平分∠AOC,∴∠AOD=∠COD,∴∠COE=∠BOE,∴OE平分∠BOC.
【针对训练】
∠BOC 和 ∠AOD
探究点3:
射线 OA 射线 OB 射线 OC 射线 OD
射线 OE 射线 OF 射线 OH 射线 OG
例4 解:
【针对训练】
1.(1) 北偏东 40° (2) 北偏西 65° (3) 南偏西 45°(西南) (4) 南偏东 20°
2.解:如图所示.
当堂检测
1. A 2.D 3. 150° 4. 62° 28°
5.解:(1)∠A+∠B=90°,∠A+∠2=90°. ∠1+∠B=90° ,∠1+∠2=90°.
(2)∠B=∠2 ( 同角的余角相等 ),∠A=∠1 ( 同角的余角相等 ).
6.解: (1)如图所示.
(2)D
4.2 直线、射线、线段
第1课时 直线、射线、线段
学习目标:1. 了解余角、补角的概念,掌握余角和补角的性质,并能利用余角、补角
的知识解决相关问题.
2. 了解方位角的概念,并能用方位角知识解决一些简单的实际问题.
重点:了解余角、补角的概念及性质,了解方位角的概念和表达方式.
难点:运用余角、补角和方位角的相关知识解题.
自主学习
教学备注:学生在课前完成自主学习部分。
一、知识链接
如图①,在长方形中,∠1+∠2= °,
∠3+∠4= °.
图①
二、新知预习
1. 如果两个角的和等于90°(直角),就说这两个角互为______ (简称为两个角______ ).
如图①,可以说∠1是∠2的余角,或∠2是∠1的余角,或∠1和∠2互余.
2. 如果两个角的和等于180°(平角),就说这两个角互为______ (简称为两个角______).
如图①,可以说∠3是∠4的补角,或∠4是∠3的补角,或∠3和∠4互补.
三、自学自测
1. 图中给出的各角,哪些互为余角?
2. 图中给出的各角,哪些互为补角?
四、我的疑惑
__________________________________________________________________________________________________________________________________________________________________
课堂探究
要点探究
探究点1:有关余角和补角的计算
例1 若一个角的补角等于它的余角的4倍,求这个角的度数.
方法总结:余补角问题中,若角之间有比较明显的倍分关系,可尝试将较小的角设为未知数,列方程解答.
例2 如图,已知O为AD上一点,∠AOC与∠AOB互补,OM,ON分别为∠AOC,∠AOB的平分线,若∠MON=40°,试求∠AOC与∠AOB的度数.
观察与思考:
∠α ∠α的余角 ∠α的补角
5°
32°
45°
77°
62°23′
x°(0<x<90)
观察可得结论:
锐角的补角比它的余角大_____.
针对训练
如果∠a=36°,那么∠a的余角等于( )
A.54° B.64° C.144° D.134°
2.如图,将一副直角三角板如图放置,若∠AOD=18°,则∠BOC的度数为_____.
第2题图 变式题图
【变式题】一副三角板按如图方式摆放,且∠1的度数比∠2的度数大44°,则∠1=______.
3.已知∠A与∠B互余,且∠A的度数比∠B度数的3倍还多30°,求∠B的度数.
探究点2:余角和补角的性质
思考:∠1 与∠2,∠3都互为补角,∠2 与∠3 的大小有什么关系?
例3 如图,O为直线AB上一点,OD平分∠AOC,∠DOE=90°.
(1)∠AOD的余角是_______________,∠COD的余角是_________________;
(2 )OE是∠BOC的平分线吗?请说明理由.
针对训练
如图,已知∠AOB=90°,∠AOC=∠BOD,则与∠AOC互余的角有__________________.
探究点3:方位角
八大方位
正东:
正南:
正西:
正北:
西北方向:
西南方向:
东北方向:
东南方向:
例4 如图,货轮O在航行过程中,发现灯塔A在它南偏东60°的方向上. 同时,在它北偏东40°,南偏西10°,西北 (即北偏西45°)方向上又分别发现了客轮B,货轮C和海岛D. 仿照表示灯塔方位的方法画出表示客轮B,货轮C和海岛D方向的射线.
针对训练
1. 如图,说出下列方位
(1) 射线 OA 表示的方向为 .
(2) 射线 OB 表示的方向为 .
(3) 射线 OC 表示的方向为 . .
(4) 射线 OD 表示的方向为 .
2.费俊龙、聂海胜乘坐“神舟”六号遨游太空时,我国当时派出远望一号~四号船队,跟踪检测. 其中远望一、二号停在太平洋洋面上,某一时刻,分别测得神舟六号在北偏东60°和北偏东30°的方向,你能在下图中画出当时神舟六号所处的位置吗?
二、课堂小结
当堂检测
1.一个角的余角是它的2倍,这个角的度数是( )
A.30° B.45° C.60° D.75°
2.下列说法正确的是( )
A.一个角的补角一定大于它本身
B.一个角的余角一定小于它本身
C.一个钝角减去一个锐角的差一定是一个锐角
D.一个角的余角一定小于其补角
3.已知∠A与∠B互余,∠B与∠C互补,若∠A=60°,则∠C的度数是_______.
4.∠1与∠2 互余,∠1 = (6x + 8)°,∠2 = (4x-8)°,则∠1= ,∠2= .
5. 如图,已知∠ACB=∠CDB=90°.
图中有哪几对互余的角?
(2) 图中哪几对角是相等的角(直角除外)?为什么?
6 垃圾打捞船A和B都停驻在湖边观测湖面,从A船发现它的北偏东60°方向有白色
漂浮物,同时,从B船也发现该白色漂浮物在它的北偏西30°方向.
(1) 试在图中确定白色漂浮物C的位置;
(2) 点C在点A的北偏东60°的方向上,那么点 A在点C的________方向上.
A. 南偏东30° B. 南偏西30°
C. 南偏东60° D. 南偏西60°
参考答案
自主学习
一、知识链接
90 180
二、新知预习
1.余角 互余 2.补角 互补
三、自学自测
1.10°和80°的角、25°和65°的角、44°和46°的角互为余角.
2.15°和165°的角、31.5°和148.5°的角、50°和130°的角、70°和110°的角互为补角.
课堂探究
一、要点探究
探究点1:
例1 解:设这个角为 x°,则它的补角是 ( 180-x )°,余角是 ( 90-x )° .
根据题意,得180-x = 4 ( 90-x ) .解得x = 60.
答:这个角的度数是60°.
例2 解:设∠AOB=x,因为∠AOC与∠AOB互补,则∠AOC=180°-x.因为OM,ON分别为∠AOC,∠AOB的平分线,所以∠AOM=(180°-x),∠AON=x.所以(180°-x)-x=40°. 解得x=50°,则180°-x=130°.即∠AOB=50°,∠AOC=130°.
观察与思考
90°
【针对训练】
1.A 2.162° 【变式题】67°
3. 解:∵∠A与∠B互余,∴∠A+∠B=90°,又∵∠A的度数比∠B度数的3倍还多30°,
∴∠A=3∠B+30°,∴3∠B+30°+∠B=90°,解得∠B=15°.故∠B的度数为15°.
探究点2:
思考 ∠2=180°-∠1,∠3=180°-∠1,∠2=∠3.
例3 解:(1)∠COE、∠BOE ∠COE、∠BOE
解:是,理由如下:∵∠DOE=90°,∴∠COD+∠COE=90°,∠AOD+∠BOE=90°,∴∠AOD+∠BOE=
∠COD+∠COE,∵OD平分∠AOC,∴∠AOD=∠COD,∴∠COE=∠BOE,∴OE平分∠BOC.
【针对训练】
∠BOC 和 ∠AOD
探究点3:
射线 OA 射线 OB 射线 OC 射线 OD
射线 OE 射线 OF 射线 OH 射线 OG
例4 解:
【针对训练】
1.(1) 北偏东 40° (2) 北偏西 65° (3) 南偏西 45°(西南) (4) 南偏东 20°
2.解:如图所示.
当堂检测
1. A 2.D 3. 150° 4. 62° 28°
5.解:(1)∠A+∠B=90°,∠A+∠2=90°. ∠1+∠B=90° ,∠1+∠2=90°.
(2)∠B=∠2 ( 同角的余角相等 ),∠A=∠1 ( 同角的余角相等 ).
6.解: (1)如图所示.
(2)D
