人教版数学七年级上册4.1.1 第2课时 从不同方向看立体图形和立体图形的展开图 学案(含答案)
文档属性
| 名称 | 人教版数学七年级上册4.1.1 第2课时 从不同方向看立体图形和立体图形的展开图 学案(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 890.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-08 00:00:00 | ||
图片预览

文档简介
第四章 几何图形初步
4.1 几何图形
4.1.1 立体图形与平面图形
第2课时 从不同的方向看立体图形和立体图形的展开图
学习目标:1. 了解立体图形与平面图形之间的联系.
2. 能画出简单立体图形从不同方向看得到的平面图形.
3. 了解研究立体图形的方法,体会一个立体图形按照不同方式展开可得到不
同的平面展开图.
4. 通过展开与折叠了解棱柱、棱锥、圆柱、圆锥、长方体、正方体的表面
展开图或根据展开图判断立体图形.
重点:了解立体图形从不同方向看能够得到平面图形,了解基本几何体与其展开图的关
系,体会一个立体图形可以有多种展开图.
难点:会画简单立体图形从不同方向看得到的平面图形,能够画出简单立体图形的展开
图,或根据展开图判断立体图形.
课堂探究
教学备注:学生在课前完成自主学习部分
要点探究
探究点1:从不同的方向看立体图形
合作探究:
画出正方体、长方体、圆柱体、圆锥、四棱锥、三棱柱从正面、左面、上面看得到的平面图形.
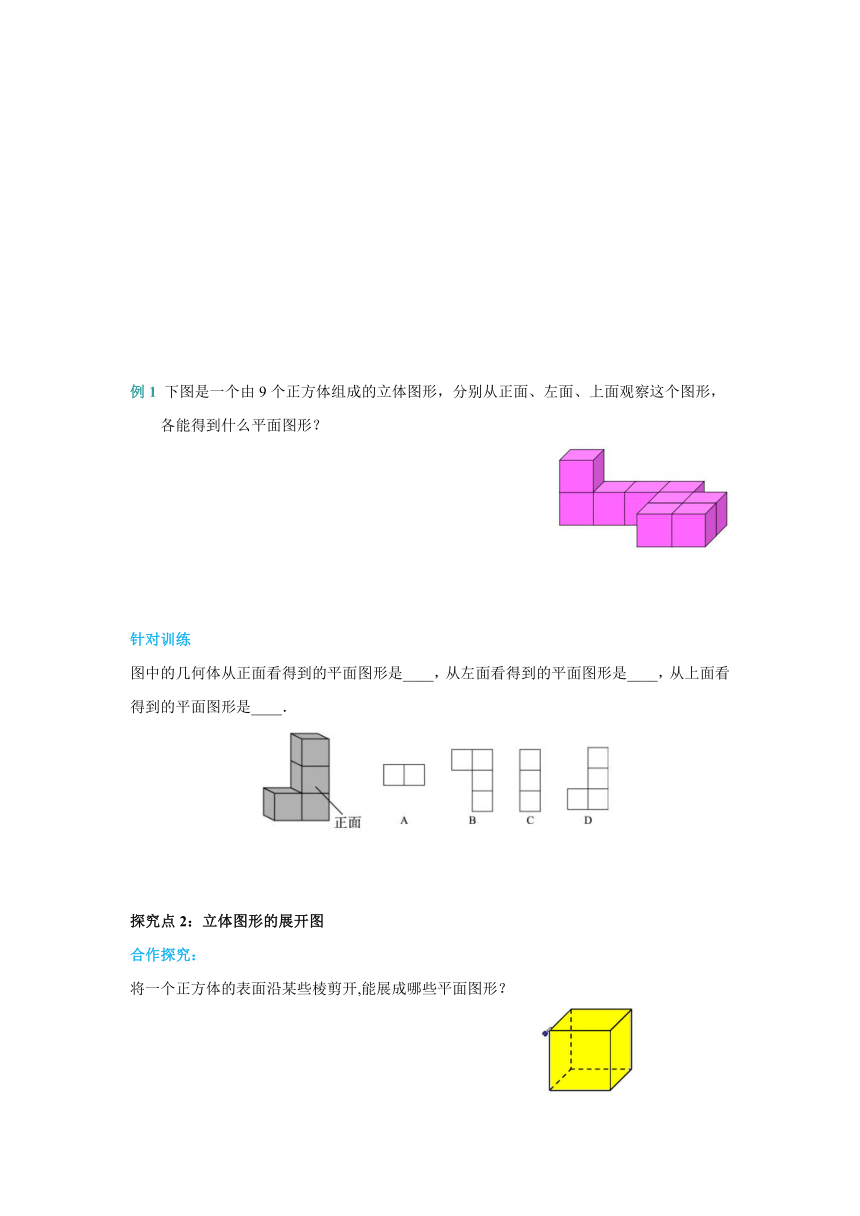
例1 下图是一个由9个正方体组成的立体图形,分别从正面、左面、上面观察这个图形,
各能得到什么平面图形?
针对训练
图中的几何体从正面看得到的平面图形是____,从左面看得到的平面图形是____,从上面看得到的平面图形是____.
探究点2:立体图形的展开图
合作探究:
将一个正方体的表面沿某些棱剪开,能展成哪些平面图形?
思考:
正方体展开图可以分为几种?
这些展开图有没有什么规律?哪些展开图可以分为一类,为什么?
要点归纳:
1.巧记正方体的展开图口诀:
正方体盒巧展开,六个面儿七刀裁,十一类图记分明;
一四一呈6种,二三一有3种,二二二与三三各1种;
对面相隔不相连,识图巧排“凹”和“田”.
2.一个正方体的展开图中,在同一直线上的相邻的三个小正方形中,首尾两个小正方形是立体图形中相对的两个面.
针对训练
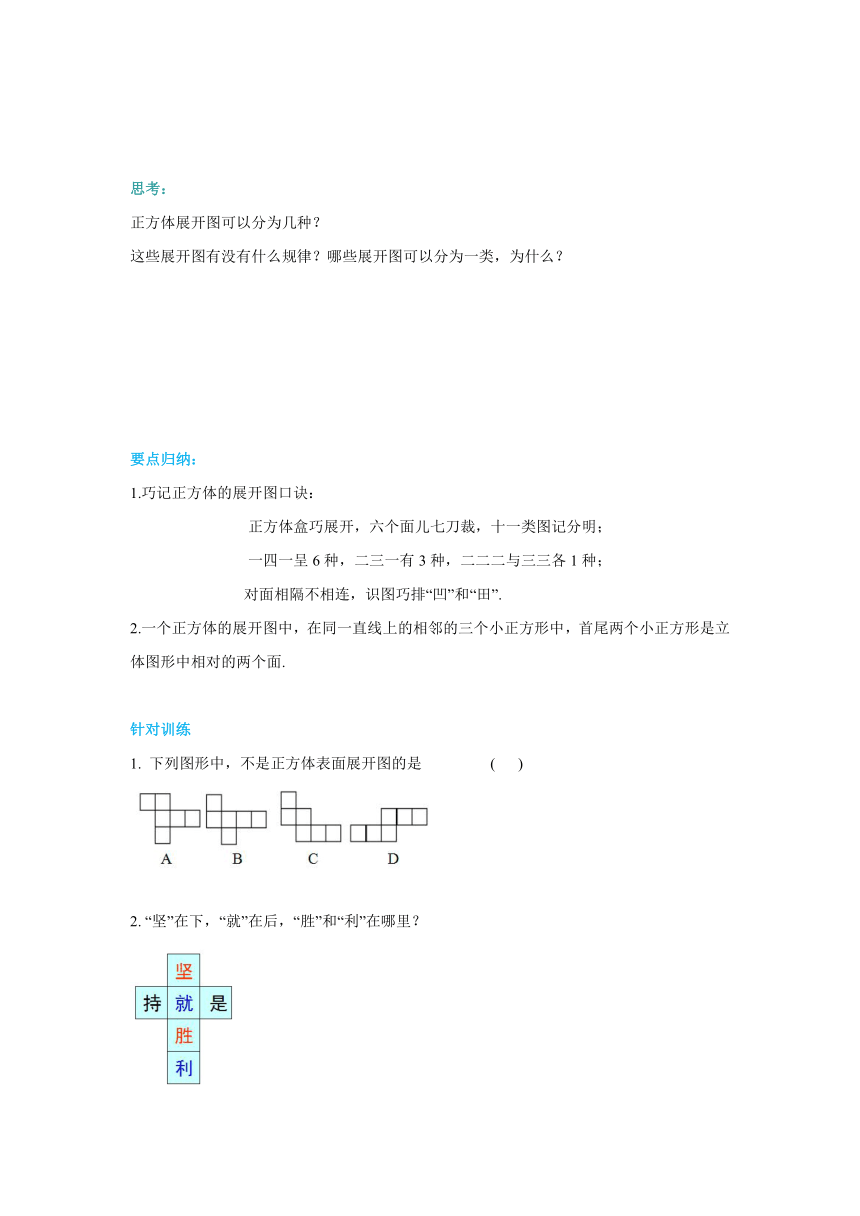
1. 下列图形中,不是正方体表面展开图的是 ( )
2. “坚”在下,“就”在后,“胜”和“利”在哪里?
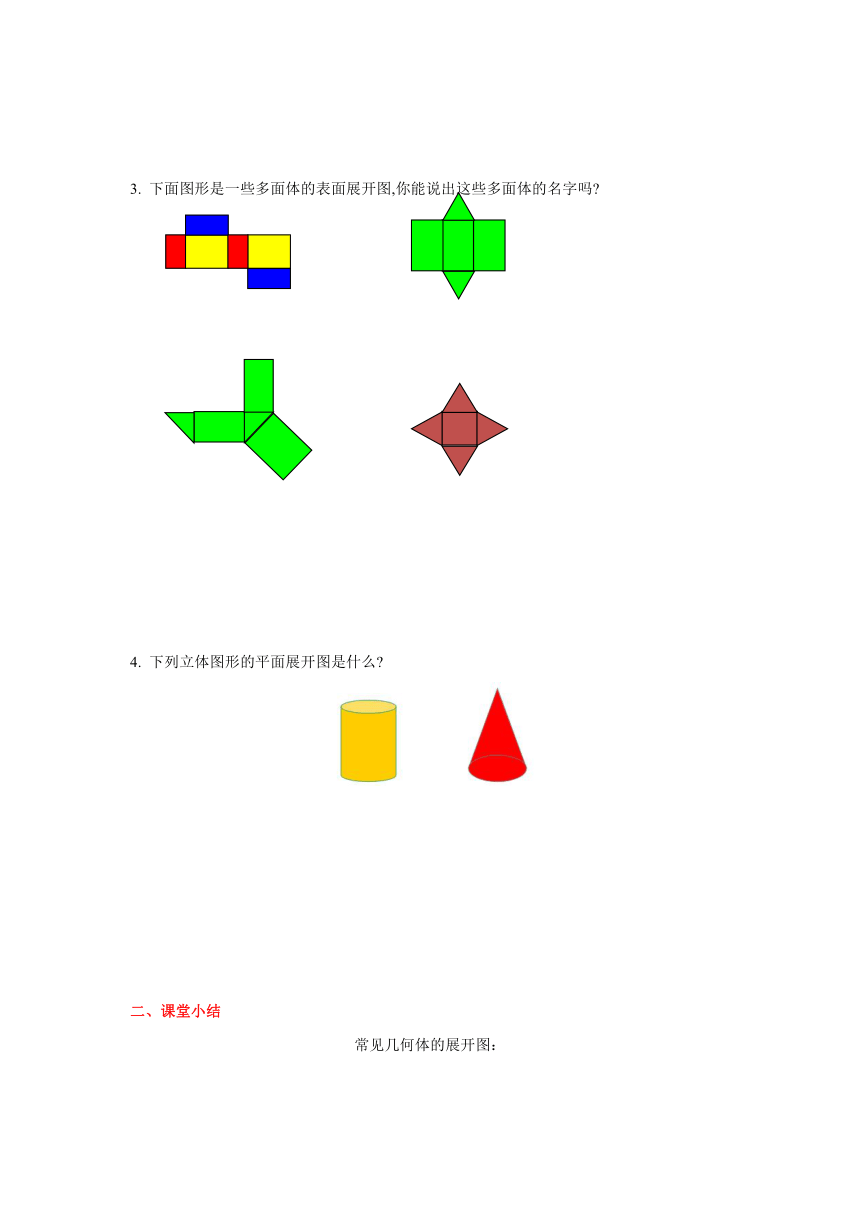
3. 下面图形是一些多面体的表面展开图,你能说出这些多面体的名字吗
4. 下列立体图形的平面展开图是什么
二、课堂小结
常见几何体的展开图:
当堂检测
1. 下图所示的从正面、上面看到的图形对应的是 ( )
2. 下图是一块带有圆形空洞和方形空洞的小木板,则下列物体中既可以堵住圆形空洞,
又可以堵住方形空洞的是 ( )
3. 下图是从由一些相同的小正方体构成的几何体的正面、左面、上面看得到的三个平面
图形,这个几何体中小正方体的个数是 ( )
A.4个
B.5个
C.6个
D.7个
4. 下列三幅平面图中,不是三棱柱的表面展开图的是 ( )
5. 如图是一个立方体纸盒的展开图,使展开图沿虚线折叠成正方体后相对面上的两个数
互为相反数,则a= ,b= ,c= .
参考答案
课堂探究
一、要点探究
探究点1:
合作探究 画图略.
例1 解:
【针对训练】
D C A
探究点2:
合作探究
思考 可分为4种.一四一有6种,二三一有3种,二二二与三三各1种.
图1~6属于“一四一”型;图7、8、9属于“二三一”型;图10属于“二二二”型;图11属于“三三”型.
【针对训练】
1.C 2. 解:“胜”在上,“利”在前.
3.解:长方体 三棱柱 三棱柱 四棱锥
4.解:展开图分别为:
当堂检测
1.B 2.B 3.B 4.B 5.-2 -7 1
4.1 几何图形
4.1.1 立体图形与平面图形
第2课时 从不同的方向看立体图形和立体图形的展开图
学习目标:1. 了解立体图形与平面图形之间的联系.
2. 能画出简单立体图形从不同方向看得到的平面图形.
3. 了解研究立体图形的方法,体会一个立体图形按照不同方式展开可得到不
同的平面展开图.
4. 通过展开与折叠了解棱柱、棱锥、圆柱、圆锥、长方体、正方体的表面
展开图或根据展开图判断立体图形.
重点:了解立体图形从不同方向看能够得到平面图形,了解基本几何体与其展开图的关
系,体会一个立体图形可以有多种展开图.
难点:会画简单立体图形从不同方向看得到的平面图形,能够画出简单立体图形的展开
图,或根据展开图判断立体图形.
课堂探究
教学备注:学生在课前完成自主学习部分
要点探究
探究点1:从不同的方向看立体图形
合作探究:
画出正方体、长方体、圆柱体、圆锥、四棱锥、三棱柱从正面、左面、上面看得到的平面图形.
例1 下图是一个由9个正方体组成的立体图形,分别从正面、左面、上面观察这个图形,
各能得到什么平面图形?
针对训练
图中的几何体从正面看得到的平面图形是____,从左面看得到的平面图形是____,从上面看得到的平面图形是____.
探究点2:立体图形的展开图
合作探究:
将一个正方体的表面沿某些棱剪开,能展成哪些平面图形?
思考:
正方体展开图可以分为几种?
这些展开图有没有什么规律?哪些展开图可以分为一类,为什么?
要点归纳:
1.巧记正方体的展开图口诀:
正方体盒巧展开,六个面儿七刀裁,十一类图记分明;
一四一呈6种,二三一有3种,二二二与三三各1种;
对面相隔不相连,识图巧排“凹”和“田”.
2.一个正方体的展开图中,在同一直线上的相邻的三个小正方形中,首尾两个小正方形是立体图形中相对的两个面.
针对训练
1. 下列图形中,不是正方体表面展开图的是 ( )
2. “坚”在下,“就”在后,“胜”和“利”在哪里?
3. 下面图形是一些多面体的表面展开图,你能说出这些多面体的名字吗
4. 下列立体图形的平面展开图是什么
二、课堂小结
常见几何体的展开图:
当堂检测
1. 下图所示的从正面、上面看到的图形对应的是 ( )
2. 下图是一块带有圆形空洞和方形空洞的小木板,则下列物体中既可以堵住圆形空洞,
又可以堵住方形空洞的是 ( )
3. 下图是从由一些相同的小正方体构成的几何体的正面、左面、上面看得到的三个平面
图形,这个几何体中小正方体的个数是 ( )
A.4个
B.5个
C.6个
D.7个
4. 下列三幅平面图中,不是三棱柱的表面展开图的是 ( )
5. 如图是一个立方体纸盒的展开图,使展开图沿虚线折叠成正方体后相对面上的两个数
互为相反数,则a= ,b= ,c= .
参考答案
课堂探究
一、要点探究
探究点1:
合作探究 画图略.
例1 解:
【针对训练】
D C A
探究点2:
合作探究
思考 可分为4种.一四一有6种,二三一有3种,二二二与三三各1种.
图1~6属于“一四一”型;图7、8、9属于“二三一”型;图10属于“二二二”型;图11属于“三三”型.
【针对训练】
1.C 2. 解:“胜”在上,“利”在前.
3.解:长方体 三棱柱 三棱柱 四棱锥
4.解:展开图分别为:
当堂检测
1.B 2.B 3.B 4.B 5.-2 -7 1
