人教版九上 24.1.3弧.弦.圆心角课件[上学期]
文档属性
| 名称 | 人教版九上 24.1.3弧.弦.圆心角课件[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 384.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-10-25 13:03:00 | ||
图片预览




文档简介
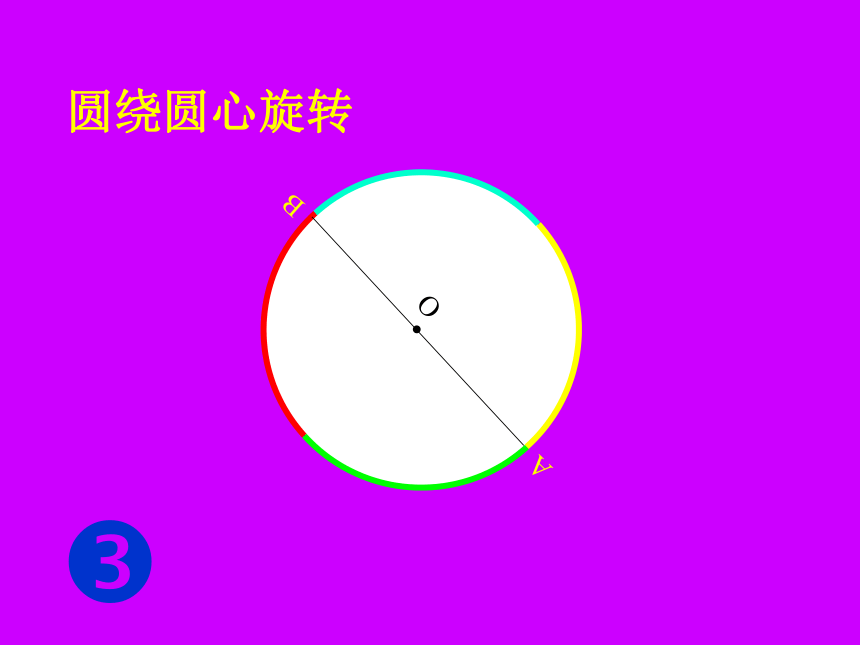
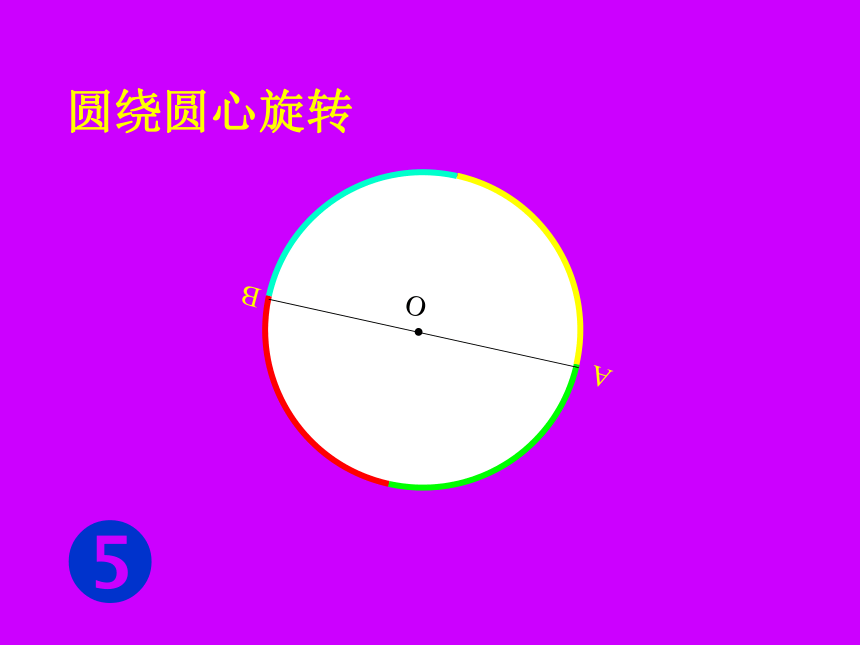
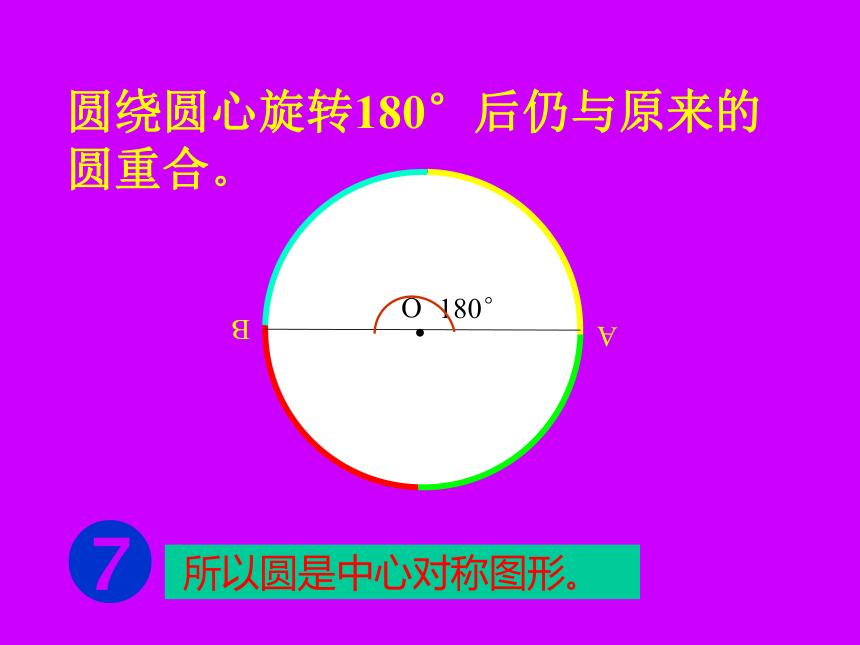
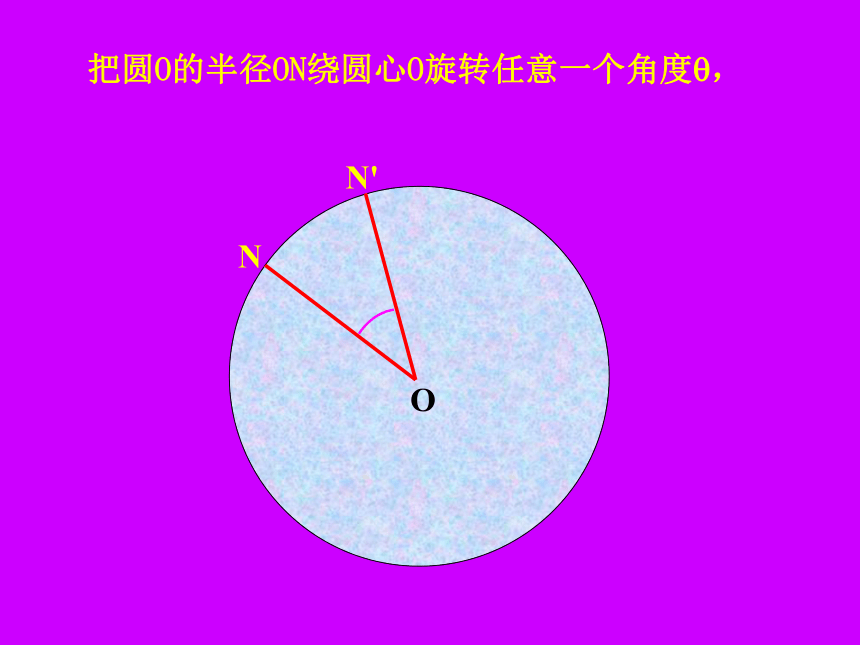
课件48张PPT。24.1.3弧.弦.圆心角AB圆绕圆心旋转?圆绕圆心旋转?圆绕圆心旋转?圆绕圆心旋转?BA圆绕圆心旋转?圆绕圆心旋转?圆绕圆心旋转?BA180° 所以圆是中心对称图形。圆绕圆心旋转180°后仍与原来的圆重合。?NO把圆O的半径ON绕圆心O旋转任意一个角度?,NON'?把圆O的半径ON绕圆心O旋转任意一个角度?,NON'?把圆O的半径ON绕圆心O旋转任意一个角度?,NON'?把圆绕圆心旋转任意一个角度后,仍与原来的圆重合。把圆O的半径ON绕圆心O旋转任意一个角度?,由此可以看出,点N'仍落在圆上。如图中所示, ∠ NO N '就是一个圆心角。NON'?定义:顶点在圆心的角叫圆心角。1、判别下列各图中的角是不是圆心角,并说明理由。①②③④ABCDo下面我们一起来观察一下:在⊙O中有哪些圆心角?(请举出两个例子,并说出圆心角所对的弧,弦。)?如果: ∠AOB=∠ CODABCDo下面我们一起来观察一下圆心角与它所对的弦、弧有什么关系??如图: ∠AOB=∠ CODABCDo下面我们一起来观察一下圆心角与它所对的弦、弧有什么关系??如图: ∠AOB=∠CODABCDo下面我们一起来观察一下圆心角与它所对的弦、弧有什么关系??ABCDo下面我们一起来观察一下圆心角与它所对的弦、弧有什么关系??ABCDo下面我们一起来观察一下圆心角与它所对的弦、弧有什么关系??ABCDo下面我们一起来观察一下圆心角与它所对的弦、弧有什么关系??ABCDo下面我们一起来观察一下圆心角与它所对的弦、弧有什么关系??ABCDo下面我们一起来观察一下圆心角与它所对的弦、弧有什么关系??ABCDo下面我们一起来观察一下圆心角与它所对的弦、弧有什么关系??ABCDo下面我们一起来观察一下圆心角与它所对的弦、弧有什么关系??ABCDo下面我们一起来观察一下圆心角与它所对的弦、弧有什么关系??ABCDo下面我们一起来观察一下圆心角与它所对的弦、弧有什么关系??ABCDo下面我们一起来观察一下圆心角与它所对的弦、弧有什么关系??ABCDo下面我们一起来观察一下圆心角与它所对的弦、弧有什么关系??下面我们一起来观察一下圆心角与它所对的弦、弧有什么关系??如图: ∠AOB=∠COD
证明:∵OA=OC ,OB=OD,
∠AOB=∠COD,
∴ 当点A与点C重合时,
点B与点D也重合。
∴ AB=CD,
圆心角定理:在同圆或等圆中,相等的圆心角所对的弧相等,
所对的弦也相等。 已知:如图∠AOB=∠ COD,
求证: AB=CD,AB = CD。⌒⌒推论在同圆或等圆中,如果①两个圆心角,②两条弧,③两条弦,④两条弦心距中,有一组量相等,那么它们所对应的其余各组量都分别相等.如由条件:③AB=A′B′④ OD=O′D′①∠AOB=∠A′O′B′ 抢答题
已知:如图,AB,CD是⊙O的两条弦,
OE,OF为AB、CD的弦心距,根据这
节课所学的定理及推论填空:ABCFDEO(2)如果OE=OF,那么 , , ;(4)如果AB=CD,那么 , , 。(1)如果∠AOB=∠COD,那么 , , ;∠AOB=∠COD AB=CD OE=OFOAB下面的说法正确吗?为什么?
如图,因为 ,根据圆心角、弧、弦、
弦心距的关系定理可知: ⌒⌒例1:如图,等边三角形ABC内接于⊙O,连结OA,OB,OC。(1)∠AOB、∠COB、∠AOC的度数分别为__________(2)若⊙O的半径为r,则等边ABC三角形的边长为_______例1:如图,等边三角形ABC内接于⊙O,连结OA,OB,OC。已知:如图,A,B,C,D是⊙O上的点,∠1=∠2。
求证:AC=BD例2:例3:已知:如图, AB、DE是⊙O的两条直径,C是⊙O上一点,且AD=CE。求证:BE=CE⌒⌒例4:如图, AB、CD是⊙O的两条直径。(1)顺次连结点A、C、B、D,所得的四边形是什么特殊四边形?为什么?(2)若直径为10cm,∠AOB=1200,求四边形ACBD的周长和面积。例5:如图, AB、CD是⊙O的两条直径。(3)四边形ACBD有可能为正方形吗?若有可能,当AB、CD有何位置关系时,四边形ACBD为正方形?为什么?例5:如图,顺次连结⊙O的两条直径Ac和BD的端点,所得的四边形是什么特殊四边形?如果要把直径为30cm的圆柱形原木锯成一根横截面为正方形的木材,并使截面尽可能地大,应怎样锯?如果这根原木长15m,问锯出地木材地体积为多少立方米?思考题已知:AB是⊙O直径,CD是弦,AE⊥CD,BF⊥CD
求证:EC=DF今天你学到的什么?∵把圆心角等分成360份,则每一份的圆心角是1o.同时整个圆也被分成了360份.则每一份这样的弧叫做1o的弧.这样,1o的圆心角对着1o的弧,
1o的弧对着1o的圆心角.
n o的圆心角对着no的弧,
n o的弧对着no的圆心角.性质:弧的度数和它所对圆心角的度数相等.做一做:巩固练习:如图: ⊙O的直径AB垂直于弦CD,AB与CD相交于点E,
∠ COD=1000,求BC,AD的度数ABCDOE解:∵OC=OD,OE⊥CD
∴∠1= ∠212∵∠COD=1000∴∠1=∠2=500
证明:∵OA=OC ,OB=OD,
∠AOB=∠COD,
∴ 当点A与点C重合时,
点B与点D也重合。
∴ AB=CD,
圆心角定理:在同圆或等圆中,相等的圆心角所对的弧相等,
所对的弦也相等。 已知:如图∠AOB=∠ COD,
求证: AB=CD,AB = CD。⌒⌒推论在同圆或等圆中,如果①两个圆心角,②两条弧,③两条弦,④两条弦心距中,有一组量相等,那么它们所对应的其余各组量都分别相等.如由条件:③AB=A′B′④ OD=O′D′①∠AOB=∠A′O′B′ 抢答题
已知:如图,AB,CD是⊙O的两条弦,
OE,OF为AB、CD的弦心距,根据这
节课所学的定理及推论填空:ABCFDEO(2)如果OE=OF,那么 , , ;(4)如果AB=CD,那么 , , 。(1)如果∠AOB=∠COD,那么 , , ;∠AOB=∠COD AB=CD OE=OFOAB下面的说法正确吗?为什么?
如图,因为 ,根据圆心角、弧、弦、
弦心距的关系定理可知: ⌒⌒例1:如图,等边三角形ABC内接于⊙O,连结OA,OB,OC。(1)∠AOB、∠COB、∠AOC的度数分别为__________(2)若⊙O的半径为r,则等边ABC三角形的边长为_______例1:如图,等边三角形ABC内接于⊙O,连结OA,OB,OC。已知:如图,A,B,C,D是⊙O上的点,∠1=∠2。
求证:AC=BD例2:例3:已知:如图, AB、DE是⊙O的两条直径,C是⊙O上一点,且AD=CE。求证:BE=CE⌒⌒例4:如图, AB、CD是⊙O的两条直径。(1)顺次连结点A、C、B、D,所得的四边形是什么特殊四边形?为什么?(2)若直径为10cm,∠AOB=1200,求四边形ACBD的周长和面积。例5:如图, AB、CD是⊙O的两条直径。(3)四边形ACBD有可能为正方形吗?若有可能,当AB、CD有何位置关系时,四边形ACBD为正方形?为什么?例5:如图,顺次连结⊙O的两条直径Ac和BD的端点,所得的四边形是什么特殊四边形?如果要把直径为30cm的圆柱形原木锯成一根横截面为正方形的木材,并使截面尽可能地大,应怎样锯?如果这根原木长15m,问锯出地木材地体积为多少立方米?思考题已知:AB是⊙O直径,CD是弦,AE⊥CD,BF⊥CD
求证:EC=DF今天你学到的什么?∵把圆心角等分成360份,则每一份的圆心角是1o.同时整个圆也被分成了360份.则每一份这样的弧叫做1o的弧.这样,1o的圆心角对着1o的弧,
1o的弧对着1o的圆心角.
n o的圆心角对着no的弧,
n o的弧对着no的圆心角.性质:弧的度数和它所对圆心角的度数相等.做一做:巩固练习:如图: ⊙O的直径AB垂直于弦CD,AB与CD相交于点E,
∠ COD=1000,求BC,AD的度数ABCDOE解:∵OC=OD,OE⊥CD
∴∠1= ∠212∵∠COD=1000∴∠1=∠2=500
同课章节目录
