新人教版九年级上24.2.1点和圆的位置关系[上学期]
文档属性
| 名称 | 新人教版九年级上24.2.1点和圆的位置关系[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 231.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-10-25 10:39:00 | ||
图片预览




文档简介
(共13张PPT)
24.2.1 点和圆的位置关系
观察与思考:
我国射击运动员在奥运会上屡获金牌,为我国赢得荣誉.右图是射击靶标的示意图,它是由许多同心圆(圆心相同,半径不等的圆)构成的,你知道击中靶上不同位置的成绩是如何计算的吗
想一想:
O
A
B
C
如图:圆O的半径为R则圆上各点到圆心的距离都为R.点A在圆内,点B在圆上,点C在圆外.那么,A.B.C三点到圆心的距离与R的大小关系你能确定吗?如果现在给你三个点并且这三点到圆心的距离给出了,你能确定这三点和圆的位置关系吗?
总结:
设⊙O的半径为r,点p到圆心的距离op=d,则有
点p在圆外 d>r
点p在圆上 d = r
点p在圆内 d<r
现在你能解释本节开始的观察题了吗?请你给同学们解释一下.
读做等价于
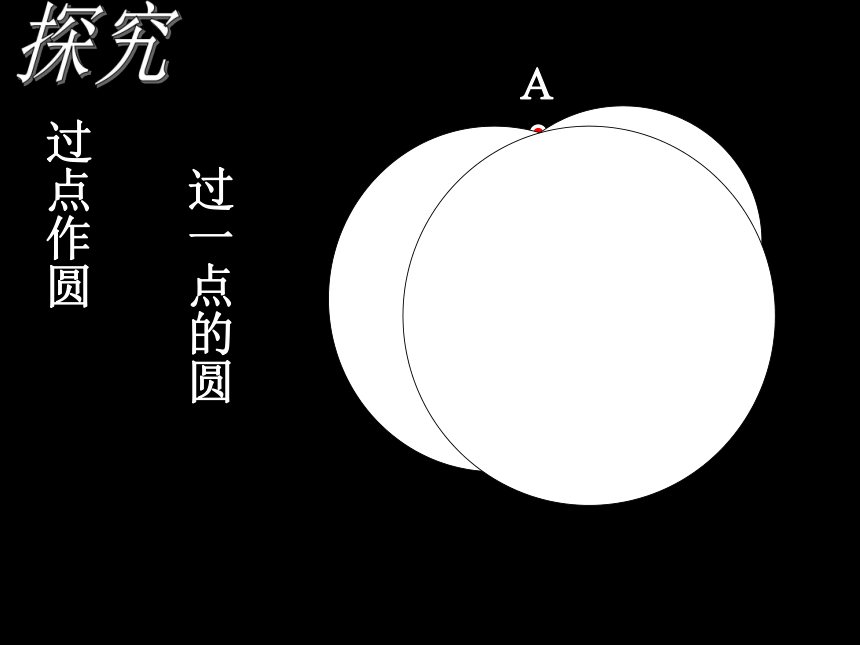
过点作圆
过一点的圆
A
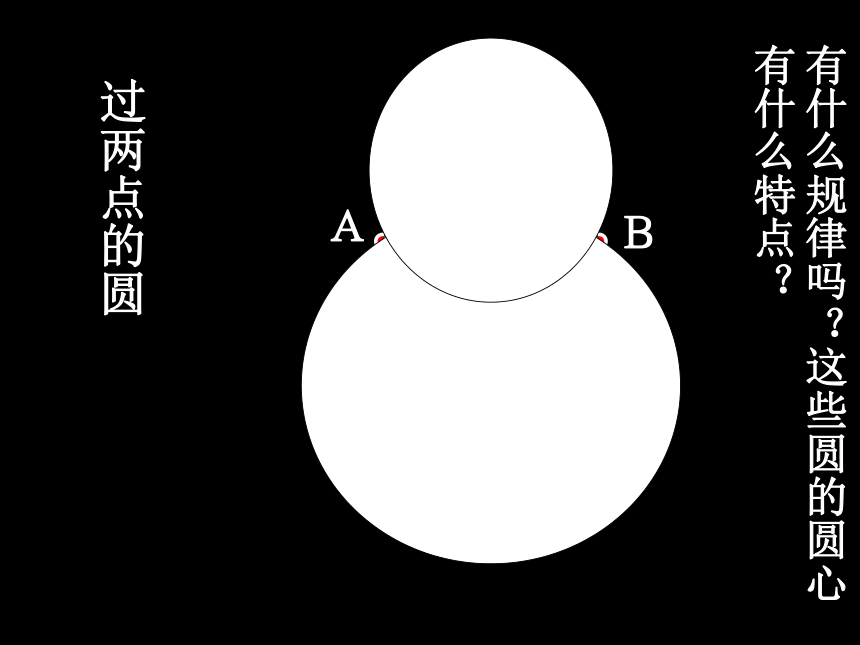
过两点的圆
A
B
有什么规律吗?这些圆的圆心有什么特点?
过三点的圆
A
B
C
O
O
你能做出吗
我们知道,过A.B.C三点的圆的圆心到A.B.C三点的距离相等.因此,我们只须确定到A.B.C三点距离相等的一点,也就是确定了圆心.
归纳:
不在同一直线上的三点确定一个圆
如上图圆O过三角形ABC的三个顶点,我们把这个圆叫做三角形的外接圆,外接圆的圆心是三角形三边垂直平分线的交点,这一点叫做这个三角形的外心.
探究:
过同一直线上的三点能确定一个圆吗
A
B
C
P
假设过同一直线L上的A.B.C三点可以作一个圆,假设这个圆的圆心为P.则点P既在线段AB的垂直平分线上,又在线段BC的垂直平分线上,是它们的交点.
我们学过“过一点有且只有一条直线与已知直线垂直”,二者相矛盾.所以,过同一直线上的三点不能作圆.
你知道吗
象上面的证明过程,它不是从已知入手直接证明得出结论,而是先假设命题成立(先假设过在同一直线上的三点可以作圆)在经过推理得出与我们前面学过的定理公理相矛盾,由矛盾断定假设不成立,从而得到原命题成立.这种方法叫做反证法.
你学到了什么
1.不在同一直线上的的三点确定一个圆
三角形的外接圆
三角形的外心
2.反证法
练一练
1.已知⊙O的半径为5cm,A为线段的中点,当OA=3cm时,点p与⊙O的位置关系是 ( )
A.点p在 ⊙O 内. B.点p在⊙O上
C.点p在⊙O外 D.不能确定
2.下列命题中,真命题的个数是( )
A.经过三点一定可以作圆 B.任意一个三角形都有一个外接圆 C.任意一个圆有且只有一个内接三角形 D.任意三角形的外心到三角形三个顶点的距离都相等
A.4个 B.3个 C.2个 D.1个
C
C
练习 100页
1.2.3.4
作业:110页 1题
24.2.1 点和圆的位置关系
观察与思考:
我国射击运动员在奥运会上屡获金牌,为我国赢得荣誉.右图是射击靶标的示意图,它是由许多同心圆(圆心相同,半径不等的圆)构成的,你知道击中靶上不同位置的成绩是如何计算的吗
想一想:
O
A
B
C
如图:圆O的半径为R则圆上各点到圆心的距离都为R.点A在圆内,点B在圆上,点C在圆外.那么,A.B.C三点到圆心的距离与R的大小关系你能确定吗?如果现在给你三个点并且这三点到圆心的距离给出了,你能确定这三点和圆的位置关系吗?
总结:
设⊙O的半径为r,点p到圆心的距离op=d,则有
点p在圆外 d>r
点p在圆上 d = r
点p在圆内 d<r
现在你能解释本节开始的观察题了吗?请你给同学们解释一下.
读做等价于
过点作圆
过一点的圆
A
过两点的圆
A
B
有什么规律吗?这些圆的圆心有什么特点?
过三点的圆
A
B
C
O
O
你能做出吗
我们知道,过A.B.C三点的圆的圆心到A.B.C三点的距离相等.因此,我们只须确定到A.B.C三点距离相等的一点,也就是确定了圆心.
归纳:
不在同一直线上的三点确定一个圆
如上图圆O过三角形ABC的三个顶点,我们把这个圆叫做三角形的外接圆,外接圆的圆心是三角形三边垂直平分线的交点,这一点叫做这个三角形的外心.
探究:
过同一直线上的三点能确定一个圆吗
A
B
C
P
假设过同一直线L上的A.B.C三点可以作一个圆,假设这个圆的圆心为P.则点P既在线段AB的垂直平分线上,又在线段BC的垂直平分线上,是它们的交点.
我们学过“过一点有且只有一条直线与已知直线垂直”,二者相矛盾.所以,过同一直线上的三点不能作圆.
你知道吗
象上面的证明过程,它不是从已知入手直接证明得出结论,而是先假设命题成立(先假设过在同一直线上的三点可以作圆)在经过推理得出与我们前面学过的定理公理相矛盾,由矛盾断定假设不成立,从而得到原命题成立.这种方法叫做反证法.
你学到了什么
1.不在同一直线上的的三点确定一个圆
三角形的外接圆
三角形的外心
2.反证法
练一练
1.已知⊙O的半径为5cm,A为线段的中点,当OA=3cm时,点p与⊙O的位置关系是 ( )
A.点p在 ⊙O 内. B.点p在⊙O上
C.点p在⊙O外 D.不能确定
2.下列命题中,真命题的个数是( )
A.经过三点一定可以作圆 B.任意一个三角形都有一个外接圆 C.任意一个圆有且只有一个内接三角形 D.任意三角形的外心到三角形三个顶点的距离都相等
A.4个 B.3个 C.2个 D.1个
C
C
练习 100页
1.2.3.4
作业:110页 1题
同课章节目录
