人教版七年级上册数学第4章 几何图形初步 章末综合训练(含答案)
文档属性
| 名称 | 人教版七年级上册数学第4章 几何图形初步 章末综合训练(含答案) | 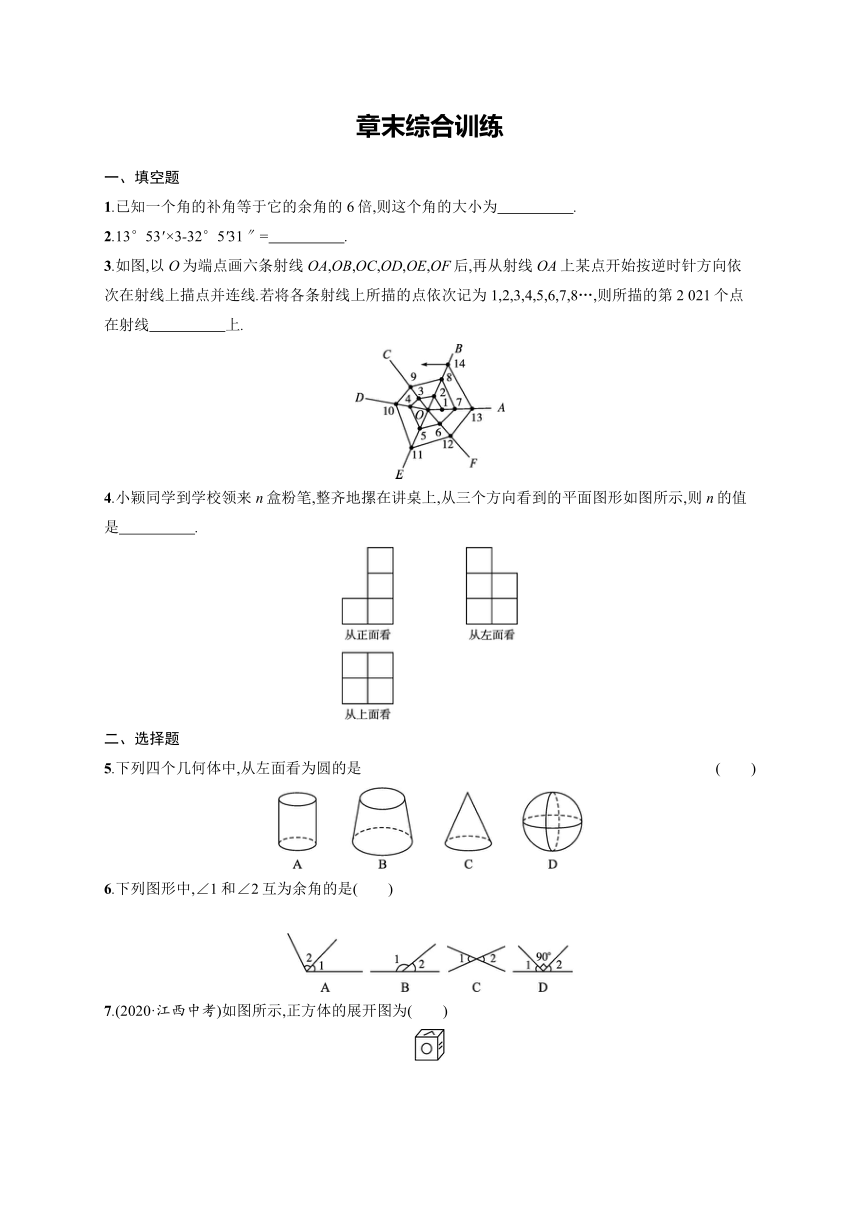 | |
| 格式 | zip | ||
| 文件大小 | 218.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-08 10:42:45 | ||
图片预览


文档简介
章末综合训练
一、填空题
1.已知一个角的补角等于它的余角的6倍,则这个角的大小为 .
2.13°53'×3-32°5'31″= .
3.如图,以O为端点画六条射线OA,OB,OC,OD,OE,OF后,再从射线OA上某点开始按逆时针方向依次在射线上描点并连线.若将各条射线上所描的点依次记为1,2,3,4,5,6,7,8…,则所描的第2 021个点在射线 上.
4.小颖同学到学校领来n盒粉笔,整齐地摞在讲桌上,从三个方向看到的平面图形如图所示,则n的值是 .
二、选择题
5.下列四个几何体中,从左面看为圆的是 ( )
6.下列图形中,∠1和∠2互为余角的是( )
7.(2020·江西中考)如图所示,正方体的展开图为( )
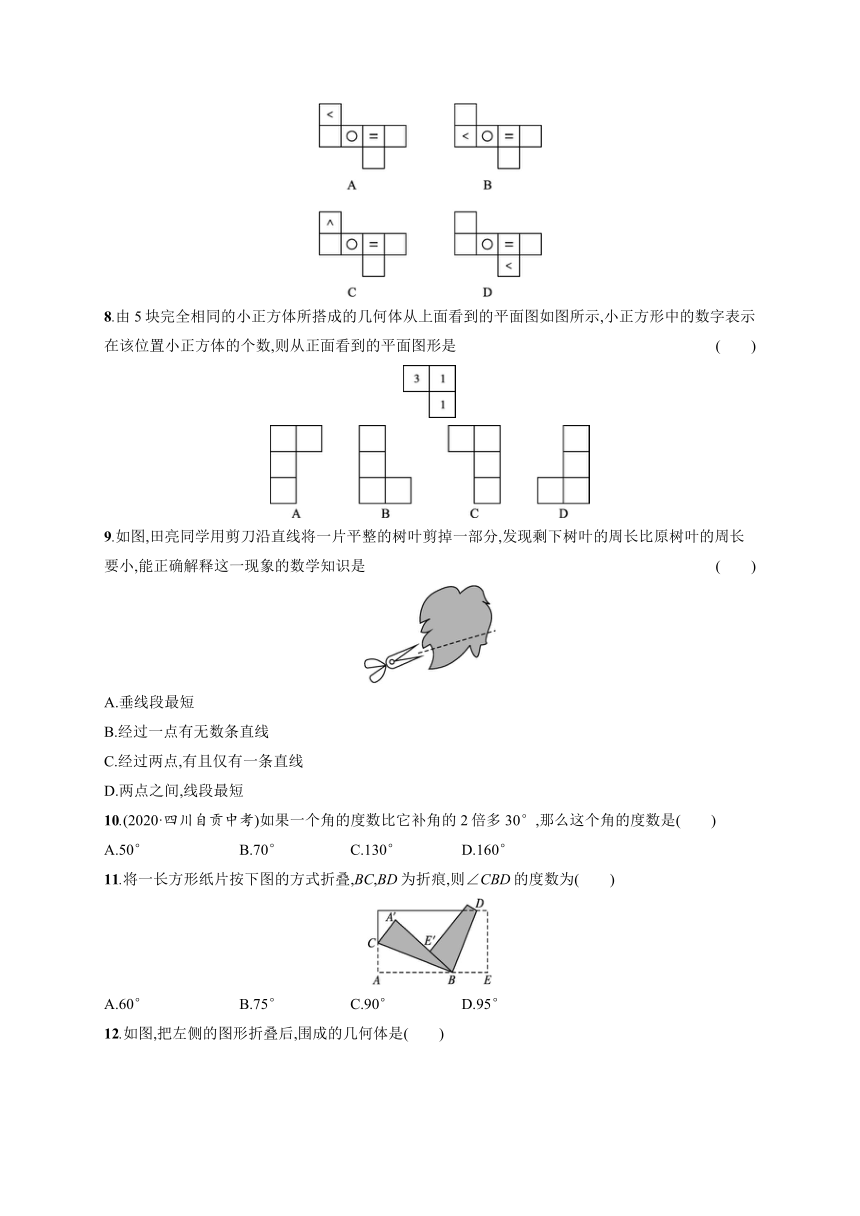
8.由5块完全相同的小正方体所搭成的几何体从上面看到的平面图如图所示,小正方形中的数字表示在该位置小正方体的个数,则从正面看到的平面图形是 ( )
9.如图,田亮同学用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长要小,能正确解释这一现象的数学知识是 ( )
A.垂线段最短
B.经过一点有无数条直线
C.经过两点,有且仅有一条直线
D.两点之间,线段最短
10.(2020·四川自贡中考)如果一个角的度数比它补角的2倍多30°,那么这个角的度数是( )
A.50° B.70° C.130° D.160°
11.将一长方形纸片按下图的方式折叠,BC,BD为折痕,则∠CBD的度数为( )
A.60° B.75° C.90° D.95°
12.如图,把左侧的图形折叠后,围成的几何体是( )
三、解答题
13.已知:线段a,b(a>b),用尺规作一条线段,使它等于3a-2b.
14.如图,在一张城市地图上有学校、医院、图书馆三地,图书馆被墨水污染,具体位置看不清,但知道图书馆在学校的东北方向,在医院的南偏东60°方向,试在图上确定图书馆的位置.
15.如图,在四边形ABCD内找一点O,使它到四边形四个顶点的距离的和(OA+OB+OC+OD)最小,并说明理由.
16.如图,已知∠AOC=60°,∠BOD=90°,∠AOB的度数是∠DOC的3倍,求∠AOB的度数.
17.如图,∠AOB=90°,OC,OD分别是∠AOE,∠BOE的平分线.
(1)求∠COD的度数;
(2)若∠AOB=α°,其他条件不变,则∠COD= °;
(3)你从(1),(2)的结果中能发现什么规律 (不必证明)
章末综合训练
一、填空题
1.72° 设这个角的大小为x°,列方程得180°-x°=6(90°-x°),解得x°=72°.
2.9°33'29″ 原式=39°159'-32°5'31″=41°38'60″-32°5'31″=9°33'29″.
3.OE 因为点在6条射线上逆时针依次循环出现,所以点的序号除以6所得余数也循环出现.2021÷6=336……5,而点5在射线OE上,所以点2021也在射线OE上.
4.7 正面看的图形有2列,每列中正方形的个数分别为1和3,故从上面看到的图形中,第1列的两个正方形分别记上1,1,第2列分别记上3,3;从左面看的图形有2列,每列中正方形个数分别为3,2,故从上面看到的图形中,第1行的两个正方形分别记上3,3,第2行分别记上2,2,取从上面看的图中每个正方形中较小的数字相加,得n=4+2+1=7.
二、选择题
5.D 6.D
7.A
8.B
9.D 由题意可知,从原图形中剪掉一部分后,其中的剪痕是线段,而剪掉部分是曲线,根据两点之间,线段最短可知,剩下树叶的周长比原树叶的周长要小.
10.C
11.C 本题考查角平分线和平角的概念.由图的折叠可知BC,BD分别是∠ABA',∠E'BE的平分线,而∠ABE是一个平角,故∠CBD=90°.
12.D 上下左右的小正方形恰好拼成正方体的一个面,且涂色部分处于斜对角的位置.
三、解答题
13.解作法:(1)作射线OM,如图所示;
(2)用圆规在射线OM上依次截取OA=AB=BC=a;
(3)用圆规在射线OM上依次截取OD=DE=b.
则线段EC就是所求作的线段,其长为3a-2b.
14.解如图,点P就是图书馆所在的位置.
15.解要使OA+OB+OC+OD最小,则点O是线段AC,BD的交点.
理由如下:如果存在不同于点O的交点P,连接PA,PB,PC,PD,那么PA+PC>AC,
即PA+PC>OA+OC,
同理,PB+PD>OB+OD,
因此PA+PB+PC+PD>OA+OB+OC+OD,
即点O是线段AC,BD的交点时,OA+OB+OC+OD之和最小.
16.解因为∠AOD=∠AOC-∠DOC=60°-∠DOC,∠BOC=∠BOD-∠DOC=90°-∠DOC,
所以∠AOB=∠AOD+∠COD+∠BOC=60°-∠DOC+∠DOC+90°-∠DOC=150°-∠DOC.
所以150°-∠DOC=3∠DOC.
所以∠DOC=37.5°.
所以∠AOB=3×37.5°=112.5°.
17.解(1)∠COD=∠COE-∠DOE=∠AOE-∠BOE=(∠AOE-∠BOE)=∠AOB=×90°=45°.
(2)α
(3)∠COD的度数总等于∠AOB的一半.
一、填空题
1.已知一个角的补角等于它的余角的6倍,则这个角的大小为 .
2.13°53'×3-32°5'31″= .
3.如图,以O为端点画六条射线OA,OB,OC,OD,OE,OF后,再从射线OA上某点开始按逆时针方向依次在射线上描点并连线.若将各条射线上所描的点依次记为1,2,3,4,5,6,7,8…,则所描的第2 021个点在射线 上.
4.小颖同学到学校领来n盒粉笔,整齐地摞在讲桌上,从三个方向看到的平面图形如图所示,则n的值是 .
二、选择题
5.下列四个几何体中,从左面看为圆的是 ( )
6.下列图形中,∠1和∠2互为余角的是( )
7.(2020·江西中考)如图所示,正方体的展开图为( )
8.由5块完全相同的小正方体所搭成的几何体从上面看到的平面图如图所示,小正方形中的数字表示在该位置小正方体的个数,则从正面看到的平面图形是 ( )
9.如图,田亮同学用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长要小,能正确解释这一现象的数学知识是 ( )
A.垂线段最短
B.经过一点有无数条直线
C.经过两点,有且仅有一条直线
D.两点之间,线段最短
10.(2020·四川自贡中考)如果一个角的度数比它补角的2倍多30°,那么这个角的度数是( )
A.50° B.70° C.130° D.160°
11.将一长方形纸片按下图的方式折叠,BC,BD为折痕,则∠CBD的度数为( )
A.60° B.75° C.90° D.95°
12.如图,把左侧的图形折叠后,围成的几何体是( )
三、解答题
13.已知:线段a,b(a>b),用尺规作一条线段,使它等于3a-2b.
14.如图,在一张城市地图上有学校、医院、图书馆三地,图书馆被墨水污染,具体位置看不清,但知道图书馆在学校的东北方向,在医院的南偏东60°方向,试在图上确定图书馆的位置.
15.如图,在四边形ABCD内找一点O,使它到四边形四个顶点的距离的和(OA+OB+OC+OD)最小,并说明理由.
16.如图,已知∠AOC=60°,∠BOD=90°,∠AOB的度数是∠DOC的3倍,求∠AOB的度数.
17.如图,∠AOB=90°,OC,OD分别是∠AOE,∠BOE的平分线.
(1)求∠COD的度数;
(2)若∠AOB=α°,其他条件不变,则∠COD= °;
(3)你从(1),(2)的结果中能发现什么规律 (不必证明)
章末综合训练
一、填空题
1.72° 设这个角的大小为x°,列方程得180°-x°=6(90°-x°),解得x°=72°.
2.9°33'29″ 原式=39°159'-32°5'31″=41°38'60″-32°5'31″=9°33'29″.
3.OE 因为点在6条射线上逆时针依次循环出现,所以点的序号除以6所得余数也循环出现.2021÷6=336……5,而点5在射线OE上,所以点2021也在射线OE上.
4.7 正面看的图形有2列,每列中正方形的个数分别为1和3,故从上面看到的图形中,第1列的两个正方形分别记上1,1,第2列分别记上3,3;从左面看的图形有2列,每列中正方形个数分别为3,2,故从上面看到的图形中,第1行的两个正方形分别记上3,3,第2行分别记上2,2,取从上面看的图中每个正方形中较小的数字相加,得n=4+2+1=7.
二、选择题
5.D 6.D
7.A
8.B
9.D 由题意可知,从原图形中剪掉一部分后,其中的剪痕是线段,而剪掉部分是曲线,根据两点之间,线段最短可知,剩下树叶的周长比原树叶的周长要小.
10.C
11.C 本题考查角平分线和平角的概念.由图的折叠可知BC,BD分别是∠ABA',∠E'BE的平分线,而∠ABE是一个平角,故∠CBD=90°.
12.D 上下左右的小正方形恰好拼成正方体的一个面,且涂色部分处于斜对角的位置.
三、解答题
13.解作法:(1)作射线OM,如图所示;
(2)用圆规在射线OM上依次截取OA=AB=BC=a;
(3)用圆规在射线OM上依次截取OD=DE=b.
则线段EC就是所求作的线段,其长为3a-2b.
14.解如图,点P就是图书馆所在的位置.
15.解要使OA+OB+OC+OD最小,则点O是线段AC,BD的交点.
理由如下:如果存在不同于点O的交点P,连接PA,PB,PC,PD,那么PA+PC>AC,
即PA+PC>OA+OC,
同理,PB+PD>OB+OD,
因此PA+PB+PC+PD>OA+OB+OC+OD,
即点O是线段AC,BD的交点时,OA+OB+OC+OD之和最小.
16.解因为∠AOD=∠AOC-∠DOC=60°-∠DOC,∠BOC=∠BOD-∠DOC=90°-∠DOC,
所以∠AOB=∠AOD+∠COD+∠BOC=60°-∠DOC+∠DOC+90°-∠DOC=150°-∠DOC.
所以150°-∠DOC=3∠DOC.
所以∠DOC=37.5°.
所以∠AOB=3×37.5°=112.5°.
17.解(1)∠COD=∠COE-∠DOE=∠AOE-∠BOE=(∠AOE-∠BOE)=∠AOB=×90°=45°.
(2)α
(3)∠COD的度数总等于∠AOB的一半.
