安徽省蚌埠市蚌山区2022-2023学年九年级上学期11月期中数学试题(含答案)
文档属性
| 名称 | 安徽省蚌埠市蚌山区2022-2023学年九年级上学期11月期中数学试题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-08 00:00:00 | ||
图片预览

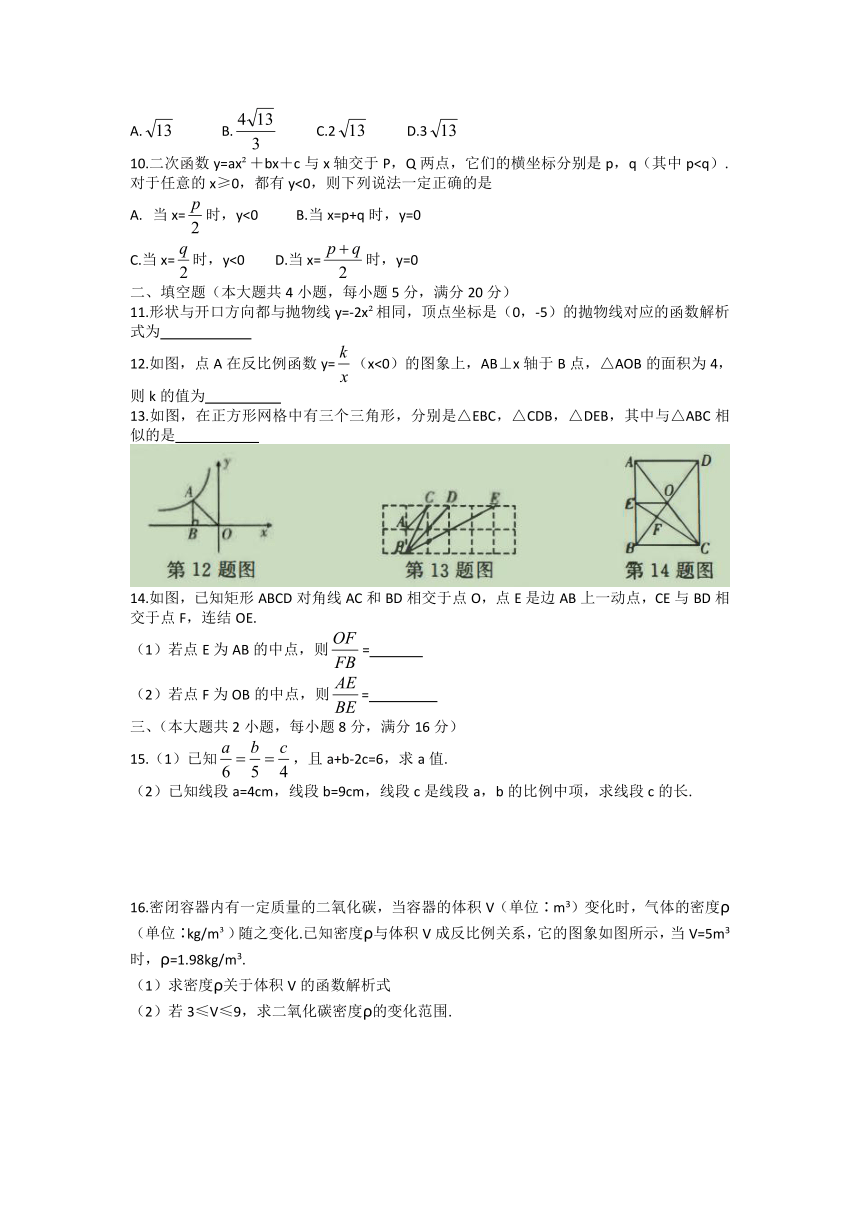
文档简介
2022——2023学年上学期九年级期中调研
数学试卷
注意事项
1.你拿到的试卷满分为150分,考试时间为120分钟。
2.试卷包括“试题卷”和“答题卷”两部分,“试题卷”共4页。“答题卷”共6页。
3.请务必在“答题卷”上答题,在“试题卷”上答题是无效的。
一、选择题(本大题共10小题,每小题4分,满分40分)
1.若,则的值为
A. B. C. D.
2.点(-3,4)在反比例函数y=上的图象上,则下列各点在此函数图象上的是
A.(2,6) B.(3,4) C.(-6,-2) D.(-4,3)
3.下列抛物线中,与抛物线y=x2-2x+4具有相同对称轴的是
A.y=4x2+2x+1 B.y=x -4x C.y=-2x +4x D.y=2x -x+4
4.下列命题中,是假命题的是
A.两个等边三角形相似 B.有一个角为20°的两个直角三角形相似
C.两个等腰直角三角形相似 D.两个直角三角形相似
5.若点A(-1,y1),B(1,y2),C(3,y3)在反比例函数y=的图像上,则y1,y2,y3的大小关系是
A.y16.大自然是美的设计师,即使是一片小小的树叶,也蕴含着“黄金分割”.如图,P为AB的黄金分割点(AP>PB),如果AB的长度为8cm,那么AP的长度是
A.4-4cm B.4-2cm C.4+4cm D.4-4cm
7.已知在△ABC中,∠A=78°,AB=4,AC=6,下列阴影部分三角形与原△ABC不一定相似的是
8.如图,AB/CD//EF,AF交BE于点G,若AC=CG,AG=FG,则下列结论错误的是
A. B. C. D.
9.如图,点A,B都在格点上(网格小正方形的边长为1),点C是线段AB与网格线的交点,则AC 的长为
A. B. C.2 D.3
10.二次函数y=ax +bx+c与x轴交于P,Q两点,它们的横坐标分别是p,q(其中p对于任意的x≥0,都有y<0,则下列说法一定正确的是
当x=时,y<0 B.当x=p+q时,y=0
C.当x=时,y<0 D.当x=时,y=0
二、填空题(本大题共4小题,每小题5分,满分20分)
11.形状与开口方向都与抛物线y=-2x 相同,顶点坐标是(0,-5)的抛物线对应的函数解析
式为
12.如图,点A在反比例函数y=(x<0)的图象上,AB⊥x轴于B点,△AOB的面积为4,
则k的值为
13.如图,在正方形网格中有三个三角形,分别是△EBC,△CDB,△DEB,其中与△ABC相似的是
14.如图,已知矩形ABCD对角线AC和BD相交于点O,点E是边AB上一动点,CE与BD相
交于点F,连结OE.
若点E为AB的中点,则=
(2)若点F为OB的中点,则=
三、(本大题共2小题,每小题8分,满分16分)
15.(1)已知,且a+b-2c=6,求a值.
(2)已知线段a=4cm,线段b=9cm,线段c是线段a,b的比例中项,求线段c的长.
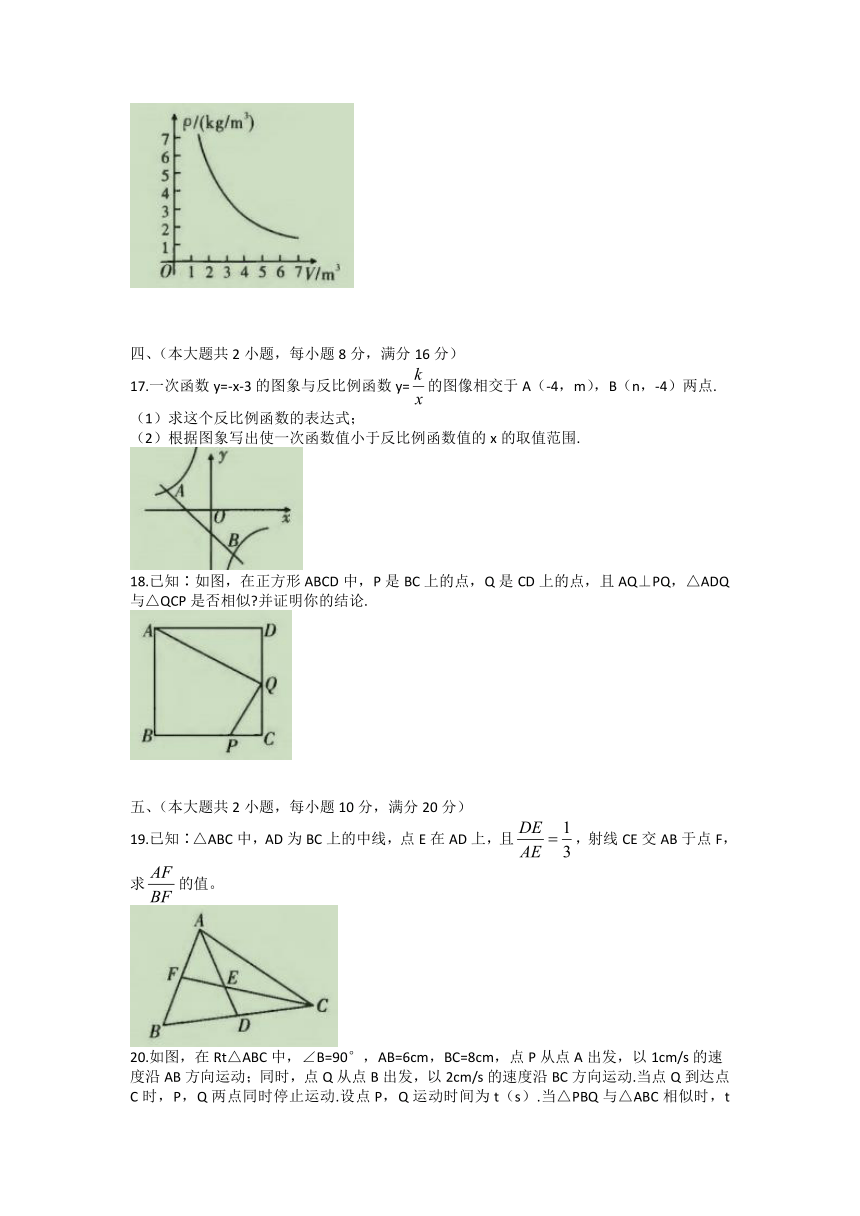
16.密闭容器内有一定质量的二氧化碳,当容器的体积V(单位∶m3)变化时,气体的密度ρ(单位∶kg/m )随之变化.已知密度ρ与体积V成反比例关系,它的图象如图所示,当V=5m3时,ρ=1.98kg/m3.
(1)求密度ρ关于体积V的函数解析式
(2)若3≤V≤9,求二氧化碳密度ρ的变化范围.
四、(本大题共2小题,每小题8分,满分16分)
17.一次函数y=-x-3的图象与反比例函数y=的图像相交于A(-4,m),B(n,-4)两点.
(1)求这个反比例函数的表达式;
(2)根据图象写出使一次函数值小于反比例函数值的x的取值范围.
18.已知∶如图,在正方形ABCD中,P是BC上的点,Q是CD上的点,且AQ⊥PQ,△ADQ与△QCP是否相似 并证明你的结论.
五、(本大题共2小题,每小题10分,满分20分)
19.已知∶△ABC中,AD为BC上的中线,点E在AD上,且,射线CE交AB于点F,求的值。
20.如图,在Rt△ABC中,∠B=90°,AB=6cm,BC=8cm,点P从点A出发,以1cm/s的速
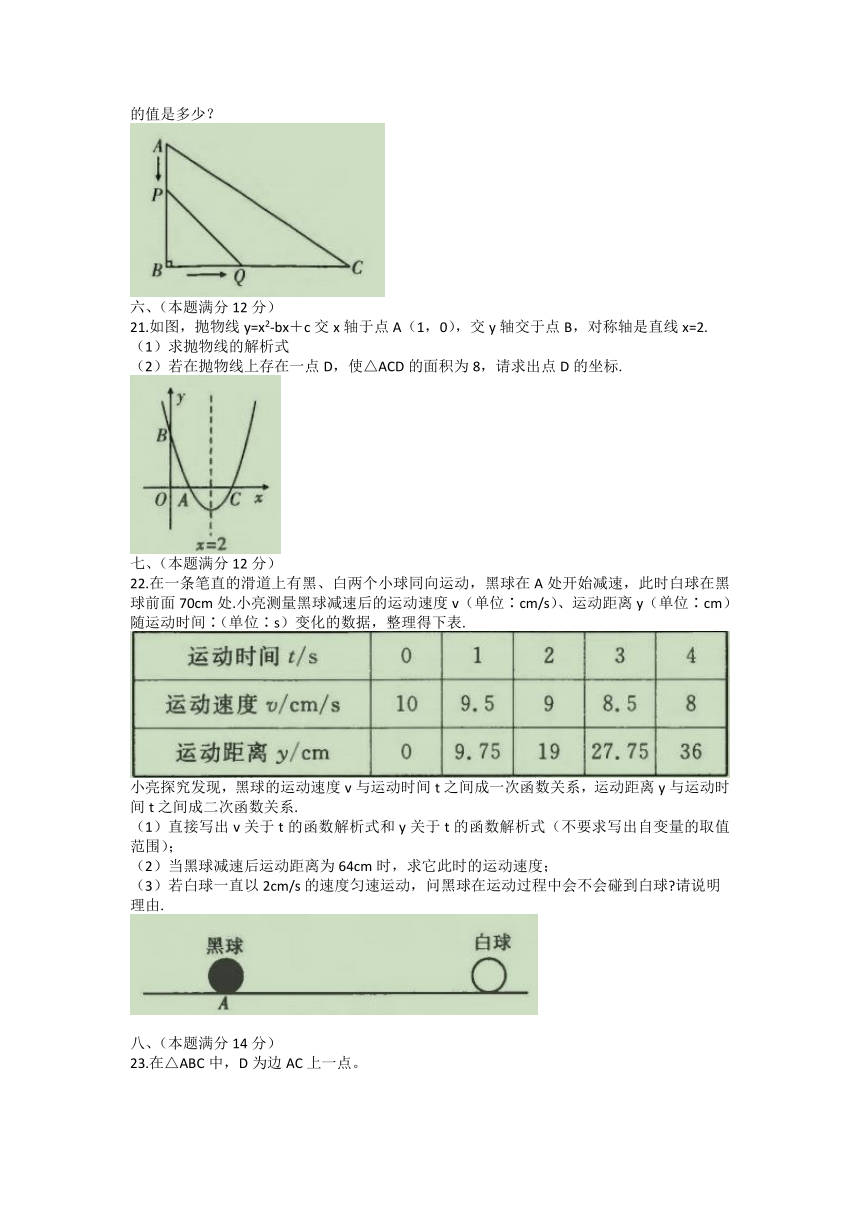
度沿AB方向运动;同时,点Q从点B出发,以2cm/s的速度沿BC方向运动.当点Q到达点C时,P,Q两点同时停止运动.设点P,Q运动时间为t(s).当△PBQ与△ABC相似时,t的值是多少?
六、(本题满分12分)
21.如图,抛物线y=x2-bx+c交x轴于点A(1,0),交y轴交于点B,对称轴是直线x=2.
(1)求抛物线的解析式
(2)若在抛物线上存在一点D,使△ACD的面积为8,请求出点D的坐标.
七、(本题满分12分)
22.在一条笔直的滑道上有黑、白两个小球同向运动,黑球在A处开始减速,此时白球在黑球前面70cm处.小亮测量黑球减速后的运动速度v(单位∶cm/s)、运动距离y(单位∶cm)随运动时间∶(单位∶s)变化的数据,整理得下表.
小亮探究发现,黑球的运动速度v与运动时间t之间成一次函数关系,运动距离y与运动时间t之间成二次函数关系.
直接写出v关于t的函数解析式和y关于t的函数解析式(不要求写出自变量的取值范围);
(2)当黑球减速后运动距离为64cm时,求它此时的运动速度;
(3)若白球一直以2cm/s的速度匀速运动,问黑球在运动过程中会不会碰到白球 请说明
理由.
八、(本题满分14分)
23.在△ABC中,D为边AC上一点。
如图1,若∠ABD=∠C,求证∶AB2=AD·AC;
(2)如图2,F为线段BD上一点,且满足∠ABD=∠ACF.
①当AC=3,AB=2,点F为BD中点时,求CD的长;
②延长CF交AB于点E,当点D为AC中点且BD=CF时,求的值.
数学试卷
注意事项
1.你拿到的试卷满分为150分,考试时间为120分钟。
2.试卷包括“试题卷”和“答题卷”两部分,“试题卷”共4页。“答题卷”共6页。
3.请务必在“答题卷”上答题,在“试题卷”上答题是无效的。
一、选择题(本大题共10小题,每小题4分,满分40分)
1.若,则的值为
A. B. C. D.
2.点(-3,4)在反比例函数y=上的图象上,则下列各点在此函数图象上的是
A.(2,6) B.(3,4) C.(-6,-2) D.(-4,3)
3.下列抛物线中,与抛物线y=x2-2x+4具有相同对称轴的是
A.y=4x2+2x+1 B.y=x -4x C.y=-2x +4x D.y=2x -x+4
4.下列命题中,是假命题的是
A.两个等边三角形相似 B.有一个角为20°的两个直角三角形相似
C.两个等腰直角三角形相似 D.两个直角三角形相似
5.若点A(-1,y1),B(1,y2),C(3,y3)在反比例函数y=的图像上,则y1,y2,y3的大小关系是
A.y1
A.4-4cm B.4-2cm C.4+4cm D.4-4cm
7.已知在△ABC中,∠A=78°,AB=4,AC=6,下列阴影部分三角形与原△ABC不一定相似的是
8.如图,AB/CD//EF,AF交BE于点G,若AC=CG,AG=FG,则下列结论错误的是
A. B. C. D.
9.如图,点A,B都在格点上(网格小正方形的边长为1),点C是线段AB与网格线的交点,则AC 的长为
A. B. C.2 D.3
10.二次函数y=ax +bx+c与x轴交于P,Q两点,它们的横坐标分别是p,q(其中p
当x=时,y<0 B.当x=p+q时,y=0
C.当x=时,y<0 D.当x=时,y=0
二、填空题(本大题共4小题,每小题5分,满分20分)
11.形状与开口方向都与抛物线y=-2x 相同,顶点坐标是(0,-5)的抛物线对应的函数解析
式为
12.如图,点A在反比例函数y=(x<0)的图象上,AB⊥x轴于B点,△AOB的面积为4,
则k的值为
13.如图,在正方形网格中有三个三角形,分别是△EBC,△CDB,△DEB,其中与△ABC相似的是
14.如图,已知矩形ABCD对角线AC和BD相交于点O,点E是边AB上一动点,CE与BD相
交于点F,连结OE.
若点E为AB的中点,则=
(2)若点F为OB的中点,则=
三、(本大题共2小题,每小题8分,满分16分)
15.(1)已知,且a+b-2c=6,求a值.
(2)已知线段a=4cm,线段b=9cm,线段c是线段a,b的比例中项,求线段c的长.
16.密闭容器内有一定质量的二氧化碳,当容器的体积V(单位∶m3)变化时,气体的密度ρ(单位∶kg/m )随之变化.已知密度ρ与体积V成反比例关系,它的图象如图所示,当V=5m3时,ρ=1.98kg/m3.
(1)求密度ρ关于体积V的函数解析式
(2)若3≤V≤9,求二氧化碳密度ρ的变化范围.
四、(本大题共2小题,每小题8分,满分16分)
17.一次函数y=-x-3的图象与反比例函数y=的图像相交于A(-4,m),B(n,-4)两点.
(1)求这个反比例函数的表达式;
(2)根据图象写出使一次函数值小于反比例函数值的x的取值范围.
18.已知∶如图,在正方形ABCD中,P是BC上的点,Q是CD上的点,且AQ⊥PQ,△ADQ与△QCP是否相似 并证明你的结论.
五、(本大题共2小题,每小题10分,满分20分)
19.已知∶△ABC中,AD为BC上的中线,点E在AD上,且,射线CE交AB于点F,求的值。
20.如图,在Rt△ABC中,∠B=90°,AB=6cm,BC=8cm,点P从点A出发,以1cm/s的速
度沿AB方向运动;同时,点Q从点B出发,以2cm/s的速度沿BC方向运动.当点Q到达点C时,P,Q两点同时停止运动.设点P,Q运动时间为t(s).当△PBQ与△ABC相似时,t的值是多少?
六、(本题满分12分)
21.如图,抛物线y=x2-bx+c交x轴于点A(1,0),交y轴交于点B,对称轴是直线x=2.
(1)求抛物线的解析式
(2)若在抛物线上存在一点D,使△ACD的面积为8,请求出点D的坐标.
七、(本题满分12分)
22.在一条笔直的滑道上有黑、白两个小球同向运动,黑球在A处开始减速,此时白球在黑球前面70cm处.小亮测量黑球减速后的运动速度v(单位∶cm/s)、运动距离y(单位∶cm)随运动时间∶(单位∶s)变化的数据,整理得下表.
小亮探究发现,黑球的运动速度v与运动时间t之间成一次函数关系,运动距离y与运动时间t之间成二次函数关系.
直接写出v关于t的函数解析式和y关于t的函数解析式(不要求写出自变量的取值范围);
(2)当黑球减速后运动距离为64cm时,求它此时的运动速度;
(3)若白球一直以2cm/s的速度匀速运动,问黑球在运动过程中会不会碰到白球 请说明
理由.
八、(本题满分14分)
23.在△ABC中,D为边AC上一点。
如图1,若∠ABD=∠C,求证∶AB2=AD·AC;
(2)如图2,F为线段BD上一点,且满足∠ABD=∠ACF.
①当AC=3,AB=2,点F为BD中点时,求CD的长;
②延长CF交AB于点E,当点D为AC中点且BD=CF时,求的值.
同课章节目录
