圆心角,弦,弧的关系[上学期]
文档属性
| 名称 | 圆心角,弦,弧的关系[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 178.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-10-26 12:07:00 | ||
图片预览


文档简介
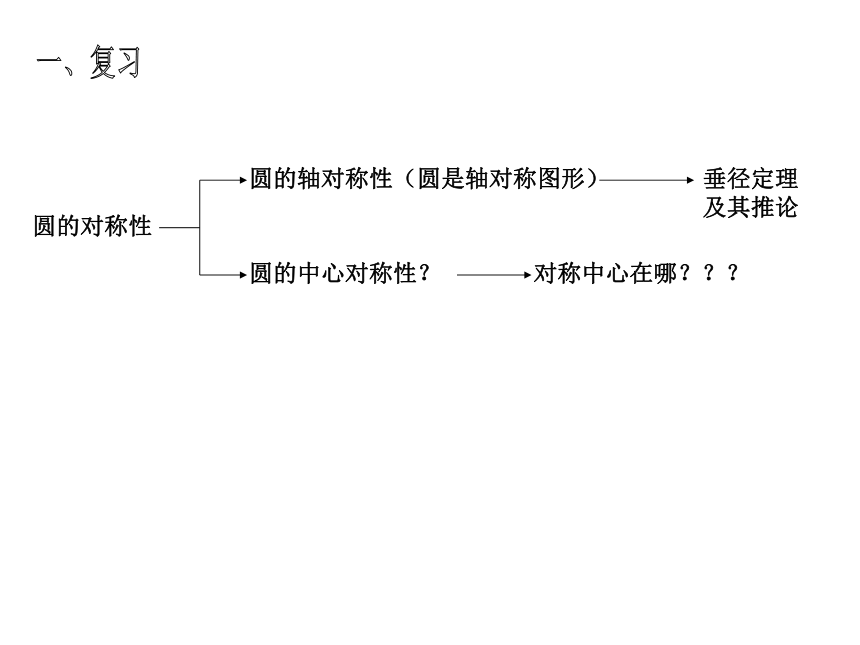
课件16张PPT。弧、弦、圆心角之间的关系实验初中圆的对称性圆的轴对称性(圆是轴对称图形)垂径定理及其推论圆的中心对称性?对称中心在哪???一、复习(一)、圆的中心对称性(1)若将圆以圆心为旋转中心,旋转180°,
你能发现什么?二、新课圆绕其圆心旋转180°后能与原来图形相重合。
因此,圆绕圆心旋转任意角度α,都能够与原来的图形重合。
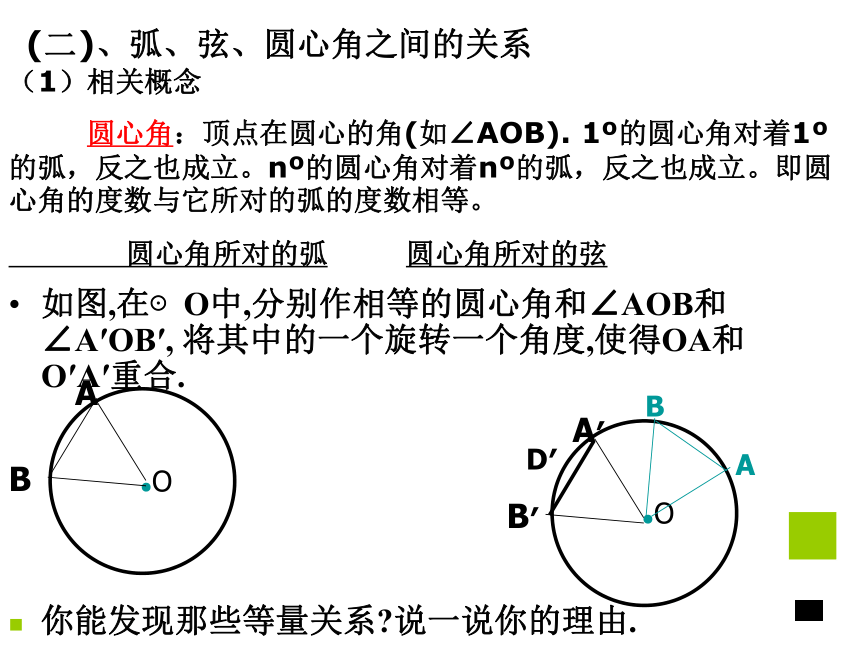
这是圆特有的一个性质:圆的旋转不变性圆是中心对称图形,对称中心是圆心。如图,在⊙O中,分别作相等的圆心角和∠AOB和∠A′OB′, 将其中的一个旋转一个角度,使得OA和O′A′重合. 你能发现那些等量关系?说一说你的理由.(1)相关概念
圆心角:顶点在圆心的角(如∠AOB). 1o的圆心角对着1o的弧,反之也成立。no的圆心角对着no的弧,反之也成立。即圆心角的度数与它所对的弧的度数相等。
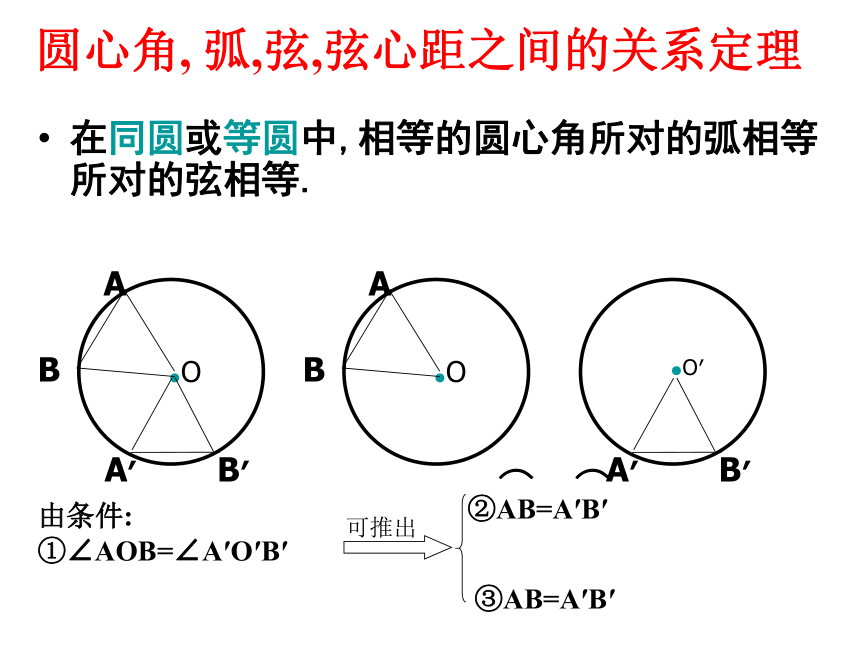
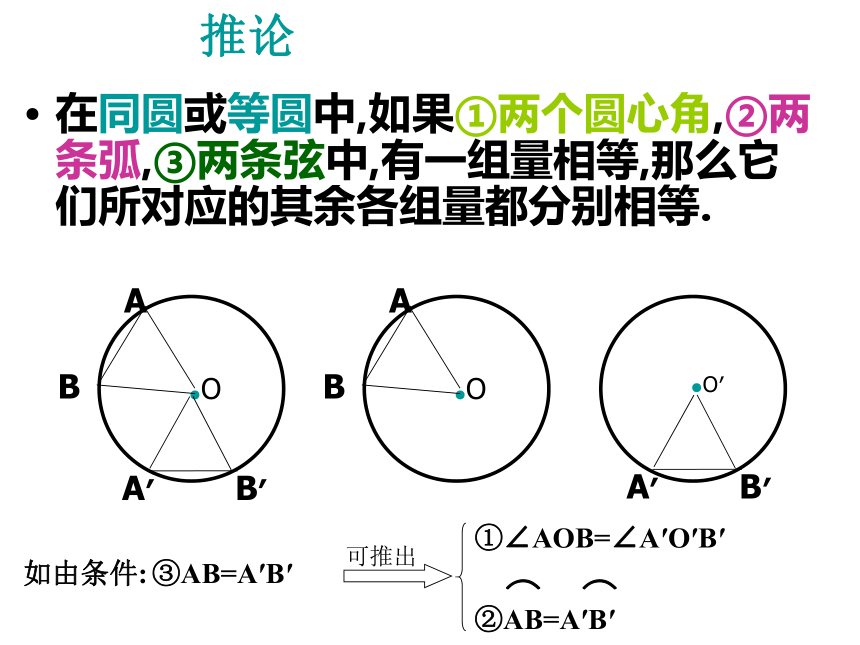
圆心角所对的弧 圆心角所对的弦(二)、弧、弦、圆心角之间的关系圆心角, 弧,弦,弦心距之间的关系定理在同圆或等圆中,相等的圆心角所对的弧相等所对的弦相等.A′B′A′B′由条件:
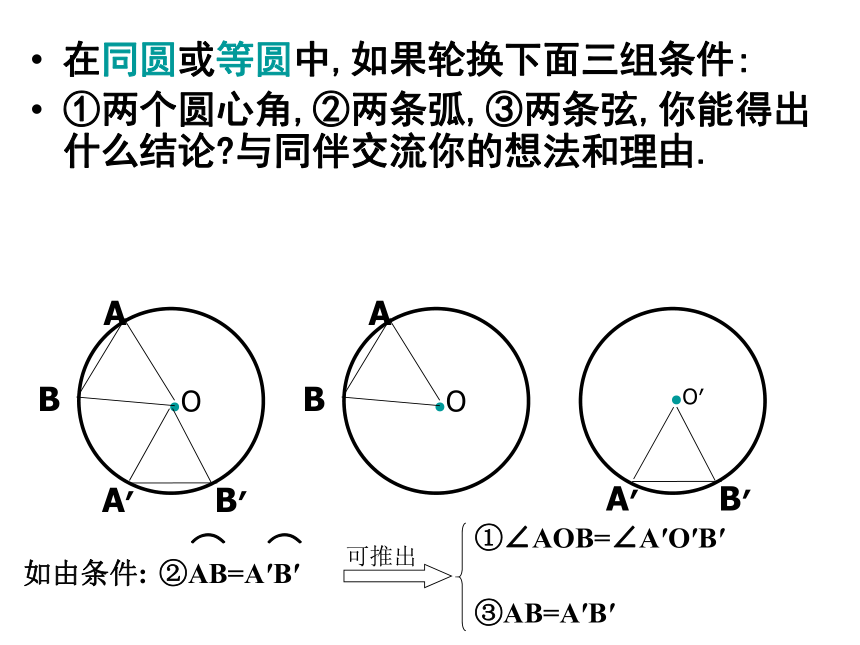
①∠AOB=∠A′O′B′③AB=A′B′在同圆或等圆中,如果轮换下面三组条件:
①两个圆心角,②两条弧,③两条弦,你能得出什么结论?与同伴交流你的想法和理由.A′B′A′B′如由条件:③AB=A′B′①∠AOB=∠A′O′B′推论在同圆或等圆中,如果①两个圆心角,②两条弧,③两条弦中,有一组量相等,那么它们所对应的其余各组量都分别相等.如由条件:③AB=A′B′①∠AOB=∠A′O′B′判断:
1、等弦所对的弧相等。 ( )
2、等弧所对的弦相等。 ( )
3、圆心角相等,所对的弦相等。( )
4、弦相等,所对的圆心角相等。( )
5、圆心角与它所对的弧相等。 ( ) ×××√×?OABCD6、在同圆或等圆中,相等的弦所对的弧相等。 ( )×三、例题1、已知:如图,AB、CD是⊙O的两条弦,根据本节定理及推论填空:
(1)如果AB=CD,那么
_____________,____________。
(2)如果AB=CD 那么
______________,____________。
(3)如果∠AOB=∠COD,那么
_____________,____ _____。
(4)如果AB=CD,OE⊥AB于E,OF⊥CD于F,OE与OF相等吗?为什么?
⌒
⌒
1.已知A,B是⊙O上的两点,∠AOB=1200,C是 的
中点,试确定四边形OACB的形状,并说明理由.
2.在⊙O中, = ,∠ACB=60°,求证∠AOB=∠BOC=∠AOC.
3.如图,AB是⊙O的直径, = = ,∠COD=35°
,求AOE的度数。
利用一个圆及若干条弦分别设计出符合下列条件的图案:
(1)是轴对称图形但不是中心对称图形;
(2)即是轴对称图形又是中心对称图形.
3.日常生活中的许多图案或现象都与圆的对称性有关,试举几例.拓展延伸:1、如图,在两同心圆中,∠AOB=∠COD,则( )
A.AB = CD B.AB的长度=CD的长度
C.AB的度数=CD的度数 D.AB < CD
2、如图,已知在Rt△ABC中,∠C=90o,∠B=25o,以C为圆心,
CA长为半径的圆交AB于D,则AD的度数是________。
课堂练习:
3.如图,以O为圆的两个同心圆中,大圆的弦CD交
小圆于点E、F,OE、OF的延长线交大圆于A、B。
求证:AC=BD。
4.如图,AB是⊙O直径,AC 、AD 是弦,且AB平分∠CAD.
求证:AC=AD.1、判别下列各图中的角是不是圆心角,并说明理由。①②③④
你能发现什么?二、新课圆绕其圆心旋转180°后能与原来图形相重合。
因此,圆绕圆心旋转任意角度α,都能够与原来的图形重合。
这是圆特有的一个性质:圆的旋转不变性圆是中心对称图形,对称中心是圆心。如图,在⊙O中,分别作相等的圆心角和∠AOB和∠A′OB′, 将其中的一个旋转一个角度,使得OA和O′A′重合. 你能发现那些等量关系?说一说你的理由.(1)相关概念
圆心角:顶点在圆心的角(如∠AOB). 1o的圆心角对着1o的弧,反之也成立。no的圆心角对着no的弧,反之也成立。即圆心角的度数与它所对的弧的度数相等。
圆心角所对的弧 圆心角所对的弦(二)、弧、弦、圆心角之间的关系圆心角, 弧,弦,弦心距之间的关系定理在同圆或等圆中,相等的圆心角所对的弧相等所对的弦相等.A′B′A′B′由条件:
①∠AOB=∠A′O′B′③AB=A′B′在同圆或等圆中,如果轮换下面三组条件:
①两个圆心角,②两条弧,③两条弦,你能得出什么结论?与同伴交流你的想法和理由.A′B′A′B′如由条件:③AB=A′B′①∠AOB=∠A′O′B′推论在同圆或等圆中,如果①两个圆心角,②两条弧,③两条弦中,有一组量相等,那么它们所对应的其余各组量都分别相等.如由条件:③AB=A′B′①∠AOB=∠A′O′B′判断:
1、等弦所对的弧相等。 ( )
2、等弧所对的弦相等。 ( )
3、圆心角相等,所对的弦相等。( )
4、弦相等,所对的圆心角相等。( )
5、圆心角与它所对的弧相等。 ( ) ×××√×?OABCD6、在同圆或等圆中,相等的弦所对的弧相等。 ( )×三、例题1、已知:如图,AB、CD是⊙O的两条弦,根据本节定理及推论填空:
(1)如果AB=CD,那么
_____________,____________。
(2)如果AB=CD 那么
______________,____________。
(3)如果∠AOB=∠COD,那么
_____________,____ _____。
(4)如果AB=CD,OE⊥AB于E,OF⊥CD于F,OE与OF相等吗?为什么?
⌒
⌒
1.已知A,B是⊙O上的两点,∠AOB=1200,C是 的
中点,试确定四边形OACB的形状,并说明理由.
2.在⊙O中, = ,∠ACB=60°,求证∠AOB=∠BOC=∠AOC.
3.如图,AB是⊙O的直径, = = ,∠COD=35°
,求AOE的度数。
利用一个圆及若干条弦分别设计出符合下列条件的图案:
(1)是轴对称图形但不是中心对称图形;
(2)即是轴对称图形又是中心对称图形.
3.日常生活中的许多图案或现象都与圆的对称性有关,试举几例.拓展延伸:1、如图,在两同心圆中,∠AOB=∠COD,则( )
A.AB = CD B.AB的长度=CD的长度
C.AB的度数=CD的度数 D.AB < CD
2、如图,已知在Rt△ABC中,∠C=90o,∠B=25o,以C为圆心,
CA长为半径的圆交AB于D,则AD的度数是________。
课堂练习:
3.如图,以O为圆的两个同心圆中,大圆的弦CD交
小圆于点E、F,OE、OF的延长线交大圆于A、B。
求证:AC=BD。
4.如图,AB是⊙O直径,AC 、AD 是弦,且AB平分∠CAD.
求证:AC=AD.1、判别下列各图中的角是不是圆心角,并说明理由。①②③④
同课章节目录
