2006中考圆小综合[上学期]
文档属性
| 名称 | 2006中考圆小综合[上学期] |
|
|
| 格式 | rar | ||
| 文件大小 | 52.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-10-08 00:00:00 | ||
图片预览

文档简介
06中考试题圆小综合
如皋市实验初中 黄亚军
1.(2006年长沙中考试题)已知两圆的半径分别为7和1,当它们外切时,圆心距
为( )
A.6 B.7 C.8 D.9
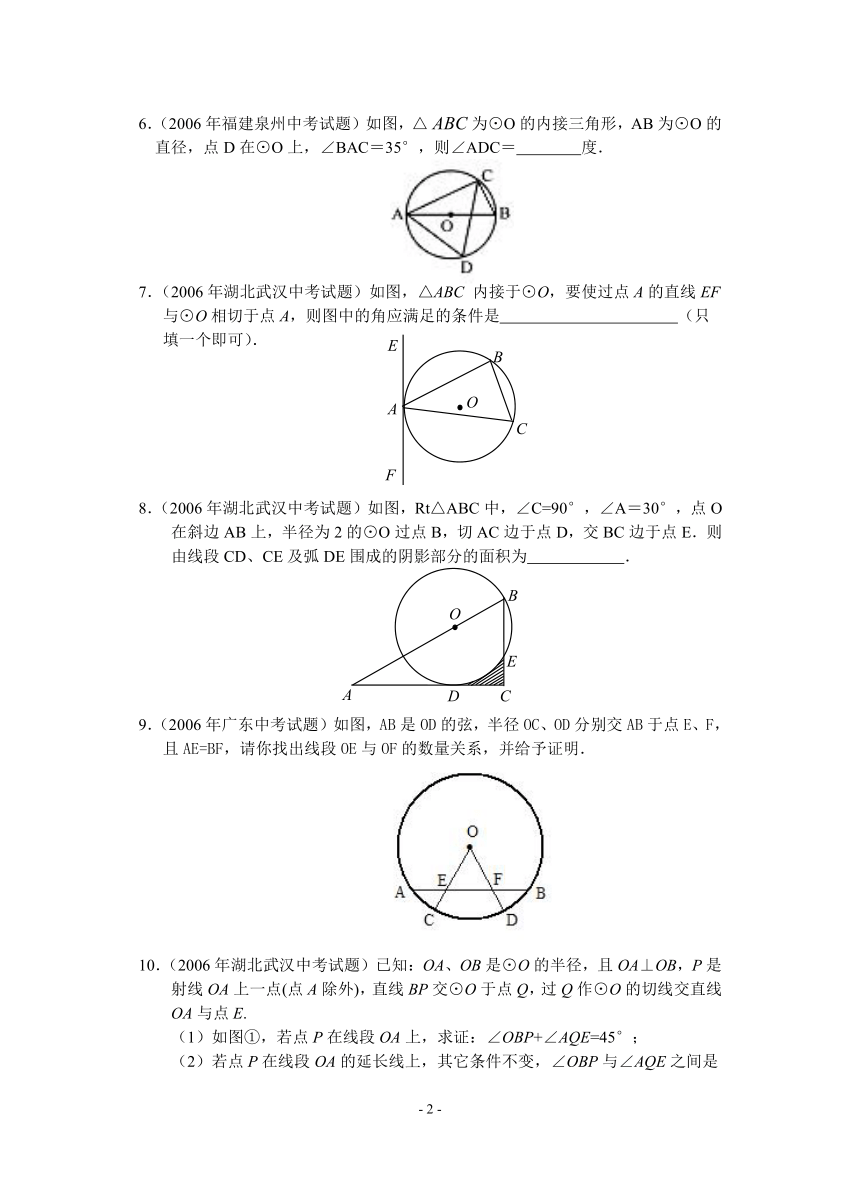
2.(2006年常州中考试题)如图,已知⊙O的半径为5,弦,则圆心O到AB的距离是( )
A.1 B.2 C.3 D.4
3.(2006年湖北武汉中考试题)如图,A、B、C是⊙O上的三点,∠AOC=100°,则∠ABC的度数为( )
A.30° B.45° C.50° D.60°
4.(2006年湖北武汉中考试题)如图,用半径R=3cm,r=2cm的钢球测量口小内大的内孔的直径D.测得钢球顶点与孔口平面的距离分别为a=4cm,b=2cm,则内孔直径D的大小为( )
A.9cm B.8cm C.7cm D.6cm
5.(2006年浙江绍兴中考试题)已知⊙O的直径AB与弦AC的夹角为35°,过C点的切线PC与AB的延长线交于点P,则么∠P等于( )
A.15° B.20° C.25° D.30°
6.(2006年福建泉州中考试题)如图,△为⊙O的内接三角形,AB为⊙O的直径,点D在⊙O上,∠BAC=35°,则∠ADC= 度.
7.(2006年湖北武汉中考试题)如图,△ABC 内接于⊙O,要使过点A的直线EF
与⊙O相切于点A,则图中的角应满足的条件是 (只
填一个即可).
8.(2006年湖北武汉中考试题)如图,Rt△ABC中,∠C=90°,∠A=30°,点O在斜边AB上,半径为2的⊙O过点B,切AC边于点D,交BC边于点E.则由线段CD、CE及弧DE围成的阴影部分的面积为 .
9.(2006年广东中考试题)如图,AB是OD的弦,半径OC、OD分别交AB于点E、F,且AE=BF,请你找出线段OE与OF的数量关系,并给予证明.
10.(2006年湖北武汉中考试题)已知:OA、OB是⊙O的半径,且OA⊥OB,P是射线OA上一点(点A除外),直线BP交⊙O于点Q,过Q作⊙O的切线交直线OA与点E.
(1)如图①,若点P在线段OA上,求证:∠OBP+∠AQE=45°;
(2)若点P在线段OA的延长线上,其它条件不变,∠OBP与∠AQE之间是
否存在某种确定的等量关系?请你完成图②,并写出结论(不需要证明).
11.(2006年江苏盐城中考试题)如图,已知:C是以AB为直径的半圆O上一点,CH⊥AB于点H,直线AC与过B点的切线相交于点D,F为BD中点,连接AF交CH于点E,直线CF交直线AB于点G.?
(1)求证:CG是⊙O的切线;
(2)若FB=FE=2,求⊙O的半径.
12.(2006年浙江嘉兴中考试题)如图,已知△ABC,AC=BC=6,∠C=90°.O是AB的中点,⊙O与AC相切于点D、与BC相切于点E.设⊙O 交OB于F,连DF并延长交CB的延长线于G.
(1)∠BFG与∠BGF是否相等?为什么?
(2)求由DG、GE和弧ED所围成图形的面积(阴影部分).
06中考试题圆小综合参考答案
1.C 2.C 3.C 4.A 5.B 6.55 7.∠BCA=∠BAE或∠ABC=∠CAF等 8.
9.解:OE=OF,
证明:连接OA,OB
∵ OA=OB ∴∠OAE=∠OBF
又∵AE=BF ∴△OAE≌△OBF ∴OE=OF
10.(1)证明:连接AB
∵QE为⊙O的切线,Q为切点,∴ ∠AQE=∠ABQ
∵OA=OB, ∴∠ABO=∠OAB=45°, ∴∠OBP+∠AQE=45°
(2)图略,∠OBP-∠AQE=45°
11.(1) 证明:连接CB、OC,
∵AB是直径,∴∠ACB=90°∵F是BD中点,
∴∠BCF=∠CBF=90°-∠CBA=∠CAB=∠ACO
∴∠OCF=90°,∴CG是⊙O的切线
(2)解:由FC=FB=FE得:∠FCE=∠FEC
可证得:FA=FG,且AB=BG
由切割线定理得:(2+FG)2=BG×AG=2BG2 ①
在Rt△BGF中,由勾股定理得:BG2=FG2-BF2 ②
由①、②得:FG2-4FG-12=0
解之得:FG1=6,FG2=-2(舍去)
∴AB=BG=4 ∴⊙O的半径为2
12.(1)解:∠BFG=∠BGF
证明:连接OD,∵OD=OF,∴∠ODF=∠OFD
∵⊙O与AC相切于点D,∴OD⊥AC
又∵∠C=90°,即GC⊥AC,∴OD∥GC,∴∠BGF=∠ODF
又∵∠BFG=∠OFD,∴∠BFG=∠BGF
(2)连接OE,则ODCE为正方形且边长为3
∵∠BFG=∠BGF
∴BG=BF=OB-OF=3-3
从而CG=CB+BG=3+3
∴阴影部分的面积
=S△DCG-(S正方形ODCE-S扇形ODE)
=
D
C
E
O
B
A
F
b
a
r
R
D
B
O
C
A
A
A
B
B
O
O
P
P
E
Q
图①
图②
E
O
C
B
A
- 4 -
如皋市实验初中 黄亚军
1.(2006年长沙中考试题)已知两圆的半径分别为7和1,当它们外切时,圆心距
为( )
A.6 B.7 C.8 D.9
2.(2006年常州中考试题)如图,已知⊙O的半径为5,弦,则圆心O到AB的距离是( )
A.1 B.2 C.3 D.4
3.(2006年湖北武汉中考试题)如图,A、B、C是⊙O上的三点,∠AOC=100°,则∠ABC的度数为( )
A.30° B.45° C.50° D.60°
4.(2006年湖北武汉中考试题)如图,用半径R=3cm,r=2cm的钢球测量口小内大的内孔的直径D.测得钢球顶点与孔口平面的距离分别为a=4cm,b=2cm,则内孔直径D的大小为( )
A.9cm B.8cm C.7cm D.6cm
5.(2006年浙江绍兴中考试题)已知⊙O的直径AB与弦AC的夹角为35°,过C点的切线PC与AB的延长线交于点P,则么∠P等于( )
A.15° B.20° C.25° D.30°
6.(2006年福建泉州中考试题)如图,△为⊙O的内接三角形,AB为⊙O的直径,点D在⊙O上,∠BAC=35°,则∠ADC= 度.
7.(2006年湖北武汉中考试题)如图,△ABC 内接于⊙O,要使过点A的直线EF
与⊙O相切于点A,则图中的角应满足的条件是 (只
填一个即可).
8.(2006年湖北武汉中考试题)如图,Rt△ABC中,∠C=90°,∠A=30°,点O在斜边AB上,半径为2的⊙O过点B,切AC边于点D,交BC边于点E.则由线段CD、CE及弧DE围成的阴影部分的面积为 .
9.(2006年广东中考试题)如图,AB是OD的弦,半径OC、OD分别交AB于点E、F,且AE=BF,请你找出线段OE与OF的数量关系,并给予证明.
10.(2006年湖北武汉中考试题)已知:OA、OB是⊙O的半径,且OA⊥OB,P是射线OA上一点(点A除外),直线BP交⊙O于点Q,过Q作⊙O的切线交直线OA与点E.
(1)如图①,若点P在线段OA上,求证:∠OBP+∠AQE=45°;
(2)若点P在线段OA的延长线上,其它条件不变,∠OBP与∠AQE之间是
否存在某种确定的等量关系?请你完成图②,并写出结论(不需要证明).
11.(2006年江苏盐城中考试题)如图,已知:C是以AB为直径的半圆O上一点,CH⊥AB于点H,直线AC与过B点的切线相交于点D,F为BD中点,连接AF交CH于点E,直线CF交直线AB于点G.?
(1)求证:CG是⊙O的切线;
(2)若FB=FE=2,求⊙O的半径.
12.(2006年浙江嘉兴中考试题)如图,已知△ABC,AC=BC=6,∠C=90°.O是AB的中点,⊙O与AC相切于点D、与BC相切于点E.设⊙O 交OB于F,连DF并延长交CB的延长线于G.
(1)∠BFG与∠BGF是否相等?为什么?
(2)求由DG、GE和弧ED所围成图形的面积(阴影部分).
06中考试题圆小综合参考答案
1.C 2.C 3.C 4.A 5.B 6.55 7.∠BCA=∠BAE或∠ABC=∠CAF等 8.
9.解:OE=OF,
证明:连接OA,OB
∵ OA=OB ∴∠OAE=∠OBF
又∵AE=BF ∴△OAE≌△OBF ∴OE=OF
10.(1)证明:连接AB
∵QE为⊙O的切线,Q为切点,∴ ∠AQE=∠ABQ
∵OA=OB, ∴∠ABO=∠OAB=45°, ∴∠OBP+∠AQE=45°
(2)图略,∠OBP-∠AQE=45°
11.(1) 证明:连接CB、OC,
∵AB是直径,∴∠ACB=90°∵F是BD中点,
∴∠BCF=∠CBF=90°-∠CBA=∠CAB=∠ACO
∴∠OCF=90°,∴CG是⊙O的切线
(2)解:由FC=FB=FE得:∠FCE=∠FEC
可证得:FA=FG,且AB=BG
由切割线定理得:(2+FG)2=BG×AG=2BG2 ①
在Rt△BGF中,由勾股定理得:BG2=FG2-BF2 ②
由①、②得:FG2-4FG-12=0
解之得:FG1=6,FG2=-2(舍去)
∴AB=BG=4 ∴⊙O的半径为2
12.(1)解:∠BFG=∠BGF
证明:连接OD,∵OD=OF,∴∠ODF=∠OFD
∵⊙O与AC相切于点D,∴OD⊥AC
又∵∠C=90°,即GC⊥AC,∴OD∥GC,∴∠BGF=∠ODF
又∵∠BFG=∠OFD,∴∠BFG=∠BGF
(2)连接OE,则ODCE为正方形且边长为3
∵∠BFG=∠BGF
∴BG=BF=OB-OF=3-3
从而CG=CB+BG=3+3
∴阴影部分的面积
=S△DCG-(S正方形ODCE-S扇形ODE)
=
D
C
E
O
B
A
F
b
a
r
R
D
B
O
C
A
A
A
B
B
O
O
P
P
E
Q
图①
图②
E
O
C
B
A
- 4 -
同课章节目录
