人教版数学八年级下册 18.2.2菱形课时2课件(共27张PPT)
文档属性
| 名称 | 人教版数学八年级下册 18.2.2菱形课时2课件(共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 491.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-08 11:09:34 | ||
图片预览



文档简介
(共27张PPT)
特殊的平行四边形
八年级下册 RJ
初中数学
18.2.2 菱形 课时2
四条边都相等
两条对角线互相垂直,并且每一条对角线平分一组对角.
轴对称图形,有两条对称轴.
菱形的特殊性质有哪些?
知识回顾
1.掌握菱形的判定及证明过程.
2.能熟练运用菱形的判定进行计算和证明.
学习目标
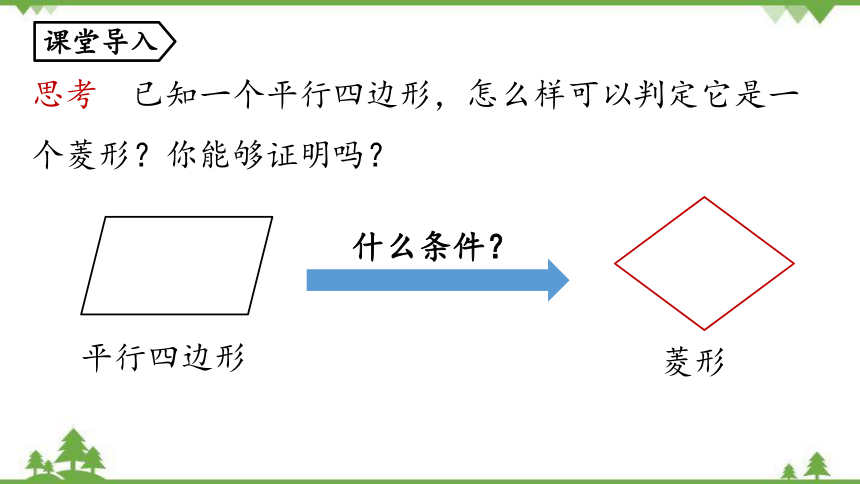
思考 已知一个平行四边形,怎么样可以判定它是一个菱形?你能够证明吗?
平行四边形
什么条件?
菱形
课堂导入
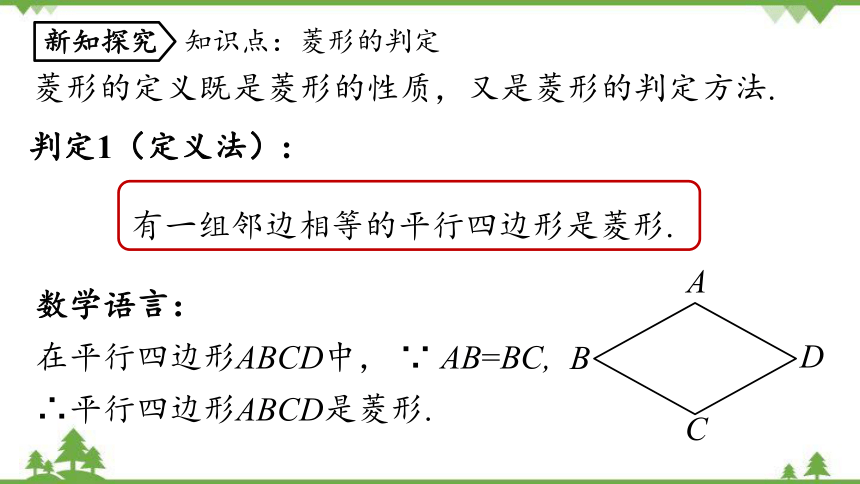
判定1(定义法):
数学语言:
在平行四边形ABCD中, ∵ AB=BC,
∴平行四边形ABCD是菱形.
A
B
D
C
菱形的定义既是菱形的性质,又是菱形的判定方法.
知识点:菱形的判定
新知探究
有一组邻边相等的平行四边形是菱形.
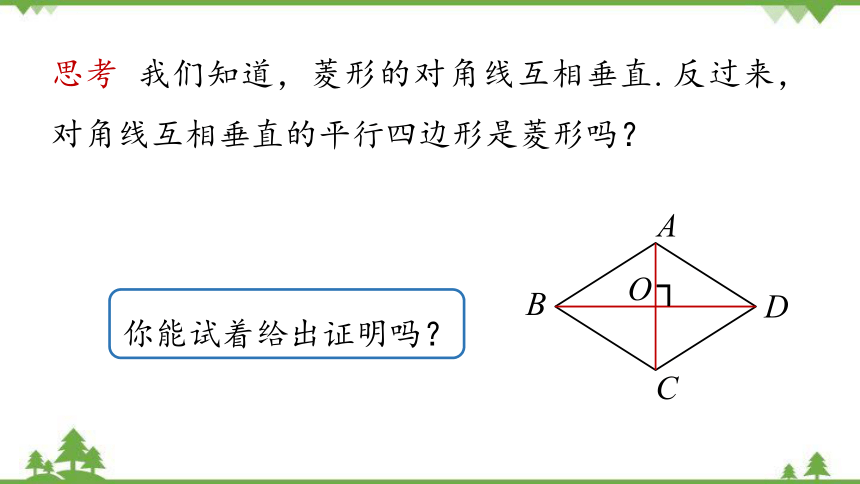
思考 我们知道,菱形的对角线互相垂直. 反过来,对角线互相垂直的平行四边形是菱形吗?
你能试着给出证明吗?
A
B
D
C
O
┐
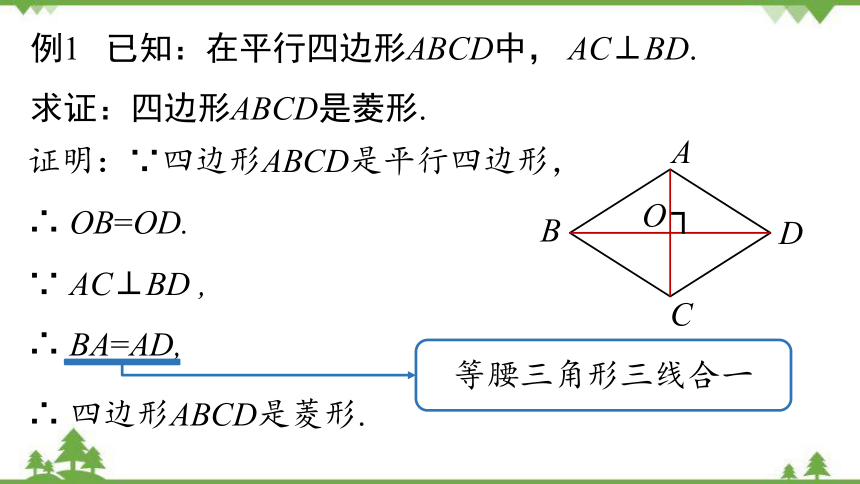
例1 已知:在平行四边形ABCD中, AC⊥BD.
求证:四边形ABCD是菱形.
证明:∵四边形ABCD是平行四边形,
∴ OB=OD.
∵ AC⊥BD ,
∴ BA=AD,
∴ 四边形ABCD是菱形.
等腰三角形三线合一
A
B
D
C
O
┐
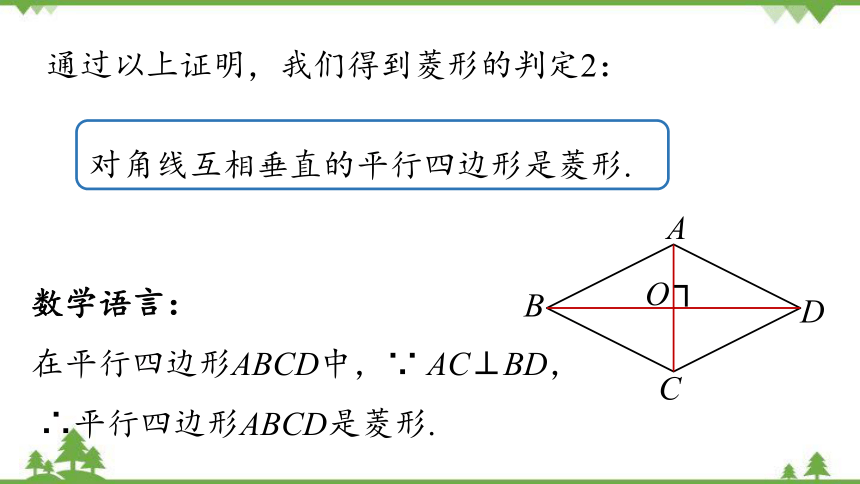
数学语言:
在平行四边形ABCD中,∵ AC⊥BD,
∴平行四边形ABCD是菱形.
A
B
D
C
O
┐
对角线互相垂直的平行四边形是菱形.
通过以上证明,我们得到菱形的判定2:
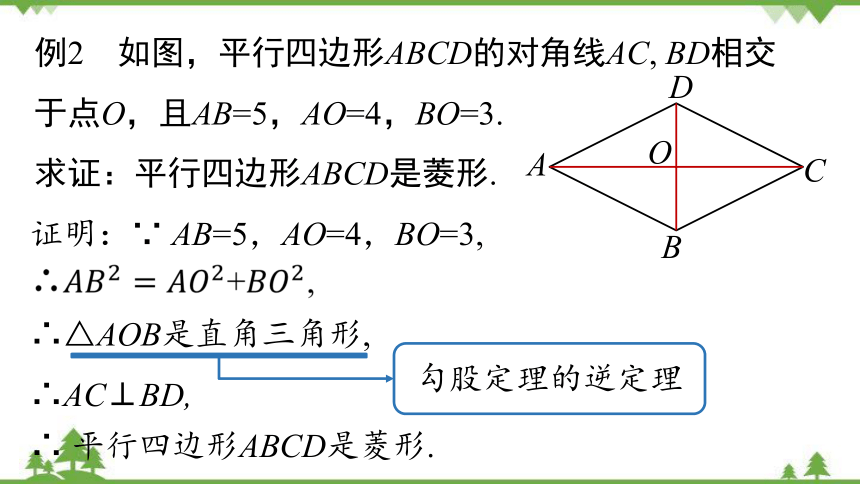
例2 如图,平行四边形ABCD的对角线AC, BD相交于点O,且AB=5,AO=4,BO=3.
求证:平行四边形ABCD是菱形.
D
A
C
B
O
证明:∵ AB=5,AO=4,BO=3,
∴△AOB是直角三角形,
∴AC⊥BD,
∴ 平行四边形ABCD是菱形.
勾股定理的逆定理
思考 动手画出一个四边形,满足有两条边相等的四边形是菱形吗?
不是
不是
?
你能进行证明吗?
三条边相等呢?
四条边相等呢?
已知:在四边形ABCD中,AB=BC=CD=DA.
求证:四边形ABCD是菱形.
证明:∵ AB=CD=BC=DA,
∴四边形ABCD是平行四边形.
∵ AB=BC,
∴四边形ABCD是菱形.
A
B
D
C
数学语言:
在四边形ABCD中,
∵ AB=BC=CD=DA,
∴四边形ABCD是菱形.
A
B
D
C
四条边相等的四边形是菱形.
通过以上证明,我们得到菱形的判定3:
判定方法 数学语言 图形
边
对角线
有一组邻边相等的平行四边形是菱形(定义)
四条边相等的四边形是菱形
∵平行四边形ABCD中,AB=BC , ∴四边形ABCD是菱形.
∵四边形ABCD中, AB=BC=CD=DA,
∴四边形ABCD是菱形.
对角线互相垂直的平行四边形是菱形.
∵平行四边形ABCD中, AC⊥BD,
∴四边形ABCD是菱形
A
B
D
C
O
┐
1.下列说法中正确的是( ).
C
A.对角线互相垂直的四边形是菱形
B.两条邻边相等,一组对角相等的四边形是菱形
C.对角线互相垂直平分的四边形是菱形
D.两条邻边相等的四边形是菱形
跟踪训练
新知探究
解析:对于选项A,对角线互相垂直的平行四边形是菱形.
对于选项B,两条邻边相等,两组对角相等的四边形是菱形.
对于选项C,两条邻边相等的平行四边形是菱形.
2.平行四边形ABCD的两对角线AC, BD相交于点O.
(1)若AB=AD,则平行四边形ABCD是 .
(2)若∠BAO=∠DAO,则平行四边形ABCD是 .
(3)若平行四边形ABCD是菱形,则AC BD.
菱形
菱形
⊥
A
B
D
C
O
要熟记菱形的判定方法哦!
1.下列条件中,能判定四边形是菱形的是( ).
A.两对角线互相垂直
B.两对角线相等
C.两对角线互相平分
D.两对角线互相垂直平分
D
随堂练习
对角线互相垂直且平分的四边形是菱形.
2.如图,在菱形ABCD中,对角线 AC, BD 交于点O,点 E, F, G, H 分别是 OA, OB, OC, OD 的中点.
求证:四边形EFGH是菱形.
D
A
B
C
O
E
F
G
H
利用三角形的中位线定理,证明四边形EFGH的四条边相等
证明: ∵四边形ABCD是菱形,
∴ AB=BC=CD=AD.
∵点E,F,G,H分别是
OA,OB,OC,OD的中点,
∴EF,FG,GH,EH分别是△AOB, △BOC, △COD, △AOD的中位线,
∴EF=FG=GH=EH,
∴四边形EFGH是菱形.
D
A
B
C
O
E
F
G
H
3.如图,在平行四边形ABCD中,E,F分别是AD,BC上的点,且DE=BF,AC⊥EF. 求证:四边形AECF是菱形.
证明:∵四边形ABCD是平行四边形,
∴ AD=BC, AD//BC.
∵ DE=BF, ∴ AE=CF.
又AE//CF, ∴四边形AECF是平行四边形.
A
B
C
D
E
F
∵ AC⊥EF ,
∴四边形AECF是菱形.
菱形的判定
判定1
判定3
有一组邻边相等的平行四边形是菱形.
判定2
四条边相等的四边形是菱形.
对角线互相垂直的平行四边形是菱形.
课堂小结
1.如图,顺次连接矩形ABCD各边中点的四边形EFGH,求证:四边形EFGH是菱形.
A
B
C
D
E
F
G
H
拓展提升
需添加辅助线构造三角形的中位线,进而证明四边形EFGH的四条边相等.
证明:连接矩形ABCD的对角线AC,BD,
∵ 四边形ABCD是矩形,
∴ AC=BD.
∵ E,F分别是BA,BC的中点,
∴ EF是△BAC的中位线,
A
B
C
D
E
F
G
H
∴ EF// HG , EH// FG, EF=FG=GH=EH,
∴ 四边形EFGH是菱形.
A
B
C
D
E
F
G
H
2. 如图,在四边形ABCD中,AD//BC,BA=BC,BD平分∠ABC.
(1)求证:四边形ABCD是菱形;
(2)过点 D 作DE⊥BD,交 BC 的延长线于点 E,若 BC=5, BD=8,求四边形ABED的周长.
A
B
C
D
E
(1)证明:∵ AD//BC, ∴∠ADB=∠CBD.
∵ BD平分∠ABC,
∴∠ADB=∠ABD,
∵ BA=BC, ∴AD=CB,
∴四边形ABCD是平行四边形.
∵ BA=BC, ∴四边形ABCD是菱形.
A
B
C
D
E
∴AD=AB.
∴∠ABD=∠CBD,
利用菱形的判定1(定义法)
(2)∵ DE⊥BD ,∴∠BDE=90
∴∠DBC+∠E=∠BDC+∠CDE=90 .
∴∠DBC=∠BDC,∴∠E=∠CDE,
∵四边形ABCD是菱形,∴CB=CD,
∴CD=CE=BC,∴BE=2BC=10.
∴ AD=AB=BC=5.
A
B
C
D
E
特殊的平行四边形
八年级下册 RJ
初中数学
18.2.2 菱形 课时2
四条边都相等
两条对角线互相垂直,并且每一条对角线平分一组对角.
轴对称图形,有两条对称轴.
菱形的特殊性质有哪些?
知识回顾
1.掌握菱形的判定及证明过程.
2.能熟练运用菱形的判定进行计算和证明.
学习目标
思考 已知一个平行四边形,怎么样可以判定它是一个菱形?你能够证明吗?
平行四边形
什么条件?
菱形
课堂导入
判定1(定义法):
数学语言:
在平行四边形ABCD中, ∵ AB=BC,
∴平行四边形ABCD是菱形.
A
B
D
C
菱形的定义既是菱形的性质,又是菱形的判定方法.
知识点:菱形的判定
新知探究
有一组邻边相等的平行四边形是菱形.
思考 我们知道,菱形的对角线互相垂直. 反过来,对角线互相垂直的平行四边形是菱形吗?
你能试着给出证明吗?
A
B
D
C
O
┐
例1 已知:在平行四边形ABCD中, AC⊥BD.
求证:四边形ABCD是菱形.
证明:∵四边形ABCD是平行四边形,
∴ OB=OD.
∵ AC⊥BD ,
∴ BA=AD,
∴ 四边形ABCD是菱形.
等腰三角形三线合一
A
B
D
C
O
┐
数学语言:
在平行四边形ABCD中,∵ AC⊥BD,
∴平行四边形ABCD是菱形.
A
B
D
C
O
┐
对角线互相垂直的平行四边形是菱形.
通过以上证明,我们得到菱形的判定2:
例2 如图,平行四边形ABCD的对角线AC, BD相交于点O,且AB=5,AO=4,BO=3.
求证:平行四边形ABCD是菱形.
D
A
C
B
O
证明:∵ AB=5,AO=4,BO=3,
∴△AOB是直角三角形,
∴AC⊥BD,
∴ 平行四边形ABCD是菱形.
勾股定理的逆定理
思考 动手画出一个四边形,满足有两条边相等的四边形是菱形吗?
不是
不是
?
你能进行证明吗?
三条边相等呢?
四条边相等呢?
已知:在四边形ABCD中,AB=BC=CD=DA.
求证:四边形ABCD是菱形.
证明:∵ AB=CD=BC=DA,
∴四边形ABCD是平行四边形.
∵ AB=BC,
∴四边形ABCD是菱形.
A
B
D
C
数学语言:
在四边形ABCD中,
∵ AB=BC=CD=DA,
∴四边形ABCD是菱形.
A
B
D
C
四条边相等的四边形是菱形.
通过以上证明,我们得到菱形的判定3:
判定方法 数学语言 图形
边
对角线
有一组邻边相等的平行四边形是菱形(定义)
四条边相等的四边形是菱形
∵平行四边形ABCD中,AB=BC , ∴四边形ABCD是菱形.
∵四边形ABCD中, AB=BC=CD=DA,
∴四边形ABCD是菱形.
对角线互相垂直的平行四边形是菱形.
∵平行四边形ABCD中, AC⊥BD,
∴四边形ABCD是菱形
A
B
D
C
O
┐
1.下列说法中正确的是( ).
C
A.对角线互相垂直的四边形是菱形
B.两条邻边相等,一组对角相等的四边形是菱形
C.对角线互相垂直平分的四边形是菱形
D.两条邻边相等的四边形是菱形
跟踪训练
新知探究
解析:对于选项A,对角线互相垂直的平行四边形是菱形.
对于选项B,两条邻边相等,两组对角相等的四边形是菱形.
对于选项C,两条邻边相等的平行四边形是菱形.
2.平行四边形ABCD的两对角线AC, BD相交于点O.
(1)若AB=AD,则平行四边形ABCD是 .
(2)若∠BAO=∠DAO,则平行四边形ABCD是 .
(3)若平行四边形ABCD是菱形,则AC BD.
菱形
菱形
⊥
A
B
D
C
O
要熟记菱形的判定方法哦!
1.下列条件中,能判定四边形是菱形的是( ).
A.两对角线互相垂直
B.两对角线相等
C.两对角线互相平分
D.两对角线互相垂直平分
D
随堂练习
对角线互相垂直且平分的四边形是菱形.
2.如图,在菱形ABCD中,对角线 AC, BD 交于点O,点 E, F, G, H 分别是 OA, OB, OC, OD 的中点.
求证:四边形EFGH是菱形.
D
A
B
C
O
E
F
G
H
利用三角形的中位线定理,证明四边形EFGH的四条边相等
证明: ∵四边形ABCD是菱形,
∴ AB=BC=CD=AD.
∵点E,F,G,H分别是
OA,OB,OC,OD的中点,
∴EF,FG,GH,EH分别是△AOB, △BOC, △COD, △AOD的中位线,
∴EF=FG=GH=EH,
∴四边形EFGH是菱形.
D
A
B
C
O
E
F
G
H
3.如图,在平行四边形ABCD中,E,F分别是AD,BC上的点,且DE=BF,AC⊥EF. 求证:四边形AECF是菱形.
证明:∵四边形ABCD是平行四边形,
∴ AD=BC, AD//BC.
∵ DE=BF, ∴ AE=CF.
又AE//CF, ∴四边形AECF是平行四边形.
A
B
C
D
E
F
∵ AC⊥EF ,
∴四边形AECF是菱形.
菱形的判定
判定1
判定3
有一组邻边相等的平行四边形是菱形.
判定2
四条边相等的四边形是菱形.
对角线互相垂直的平行四边形是菱形.
课堂小结
1.如图,顺次连接矩形ABCD各边中点的四边形EFGH,求证:四边形EFGH是菱形.
A
B
C
D
E
F
G
H
拓展提升
需添加辅助线构造三角形的中位线,进而证明四边形EFGH的四条边相等.
证明:连接矩形ABCD的对角线AC,BD,
∵ 四边形ABCD是矩形,
∴ AC=BD.
∵ E,F分别是BA,BC的中点,
∴ EF是△BAC的中位线,
A
B
C
D
E
F
G
H
∴ EF// HG , EH// FG, EF=FG=GH=EH,
∴ 四边形EFGH是菱形.
A
B
C
D
E
F
G
H
2. 如图,在四边形ABCD中,AD//BC,BA=BC,BD平分∠ABC.
(1)求证:四边形ABCD是菱形;
(2)过点 D 作DE⊥BD,交 BC 的延长线于点 E,若 BC=5, BD=8,求四边形ABED的周长.
A
B
C
D
E
(1)证明:∵ AD//BC, ∴∠ADB=∠CBD.
∵ BD平分∠ABC,
∴∠ADB=∠ABD,
∵ BA=BC, ∴AD=CB,
∴四边形ABCD是平行四边形.
∵ BA=BC, ∴四边形ABCD是菱形.
A
B
C
D
E
∴AD=AB.
∴∠ABD=∠CBD,
利用菱形的判定1(定义法)
(2)∵ DE⊥BD ,∴∠BDE=90
∴∠DBC+∠E=∠BDC+∠CDE=90 .
∴∠DBC=∠BDC,∴∠E=∠CDE,
∵四边形ABCD是菱形,∴CB=CD,
∴CD=CE=BC,∴BE=2BC=10.
∴ AD=AB=BC=5.
A
B
C
D
E
