切线长定理和三角形的内切圆[上学期]
文档属性
| 名称 | 切线长定理和三角形的内切圆[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 415.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-10-13 19:20:00 | ||
图片预览

文档简介
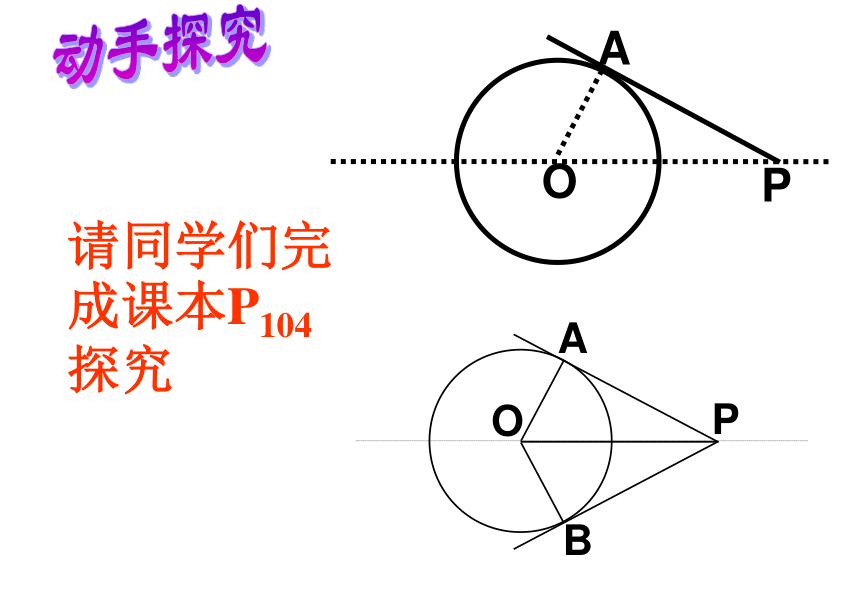
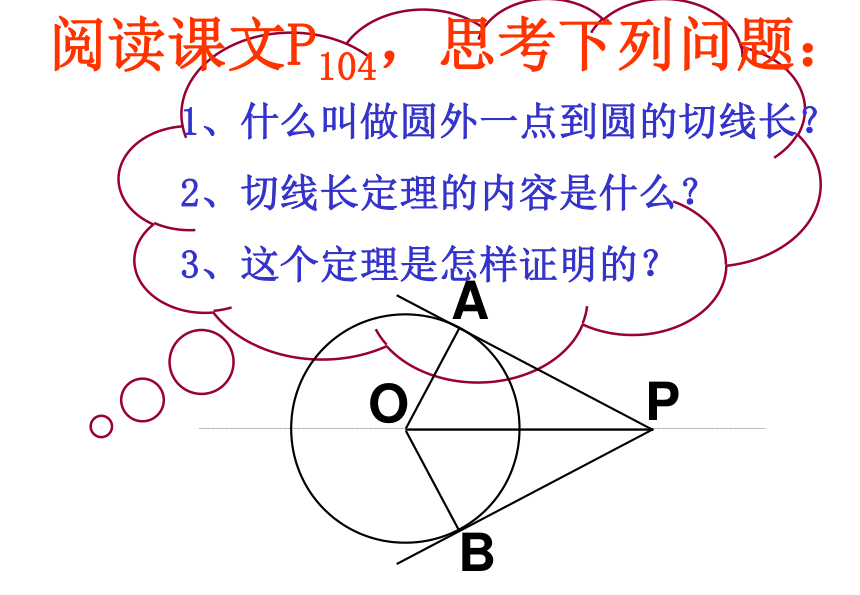
课件15张PPT。切 线 长 定 理动手探究请同学们完成课本P104探究阅读课文P104,思考下列问题:1、什么叫做圆外一点到圆的切线长?
2、切线长定理的内容是什么?
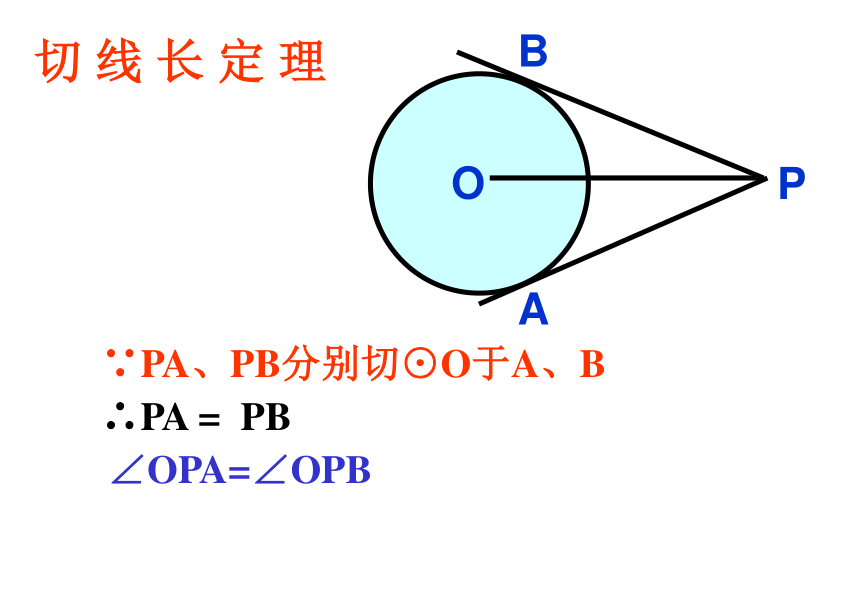
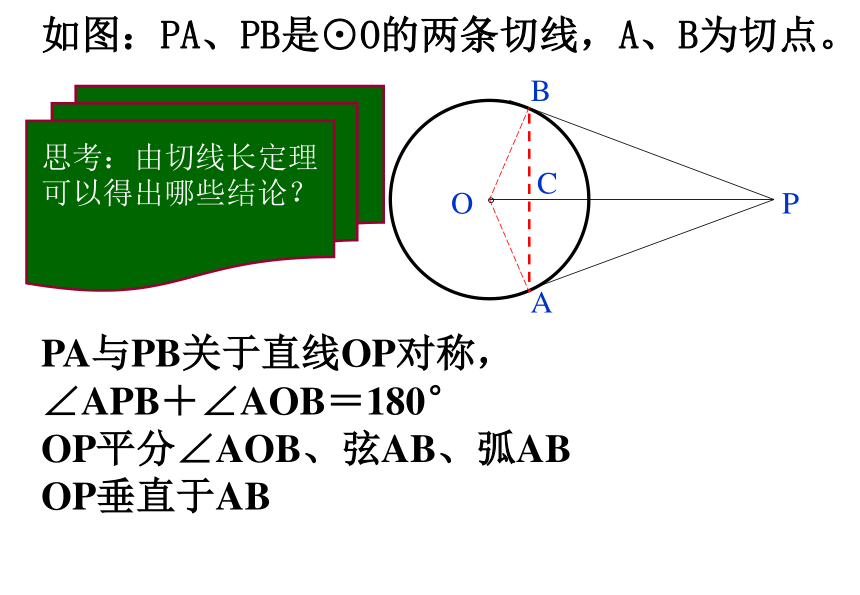
3、这个定理是怎样证明的?切 线 长 定 理∵PA、PB分别切⊙O于A、B∴PA = PB∠OPA=∠OPB。PABOC如图:PA、PB是⊙O的两条切线,A、B为切点。思考:由切线长定理可以得出哪些结论?
PA与PB关于直线OP对称,
∠APB+∠AOB=180°
OP平分∠AOB、弦AB、弧AB
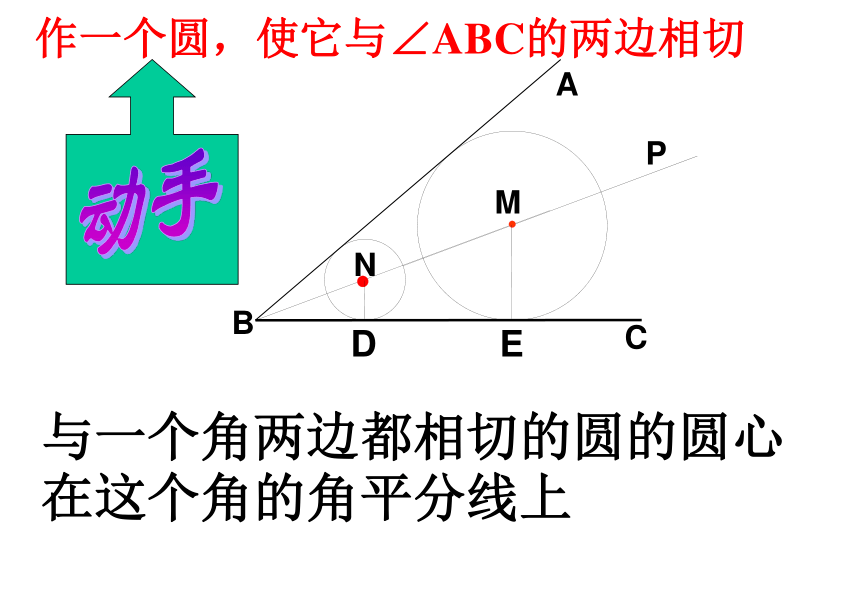
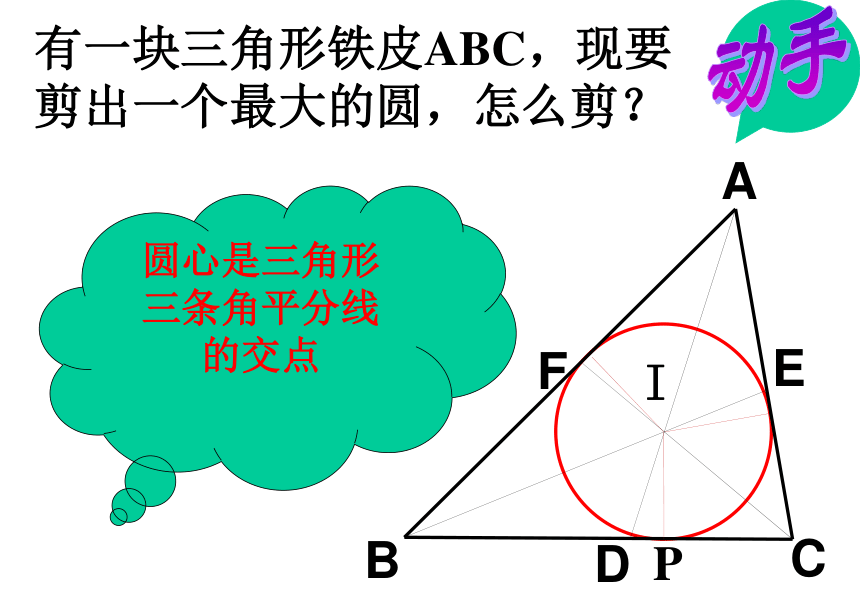
OP垂直于AB作一个圆,使它与∠ABC的两边相切与一个角两边都相切的圆的圆心在这个角的角平分线上动手I有一块三角形铁皮ABC,现要剪出一个最大的圆,怎么剪?圆心是三角形
三条角平分线
的交点 和三角形三边都相切的圆叫做三角形的内切圆,内切圆的圆心叫做三角形的内心,这个三角形叫做圆外切三角形有关概念⊙I是△ABC的 ,
点I是△ABC的 ,
△ABC是⊙I的 。内切圆内心外切三角形归纳内心的性质1、内心是三角形内切圆的圆心
2、内心到各边的距离相等
3、内心是各角平分线的交点探究与应用在△ABC中,∠A=70°
①若O是△ABC的外心,则∠BOC= ;
②若O是△ABC的内心,则∠BOC= 。
140°125°2、已知:在△ABC中,AB=14,BC=9,AC=13,它的内切圆分别和BC、AC、AB切于点D、E、F,求AF、BD和CE的长。探究与发现1、如图,哪些线段相等?设△ABC的BC=a,CA=b,AB=c,内切圆I和BC、AC、AB分别相切于点D、E、F分析:设 AF=x,BD=y,CE=z 例:直角三角形的两直角边分别是5cm, 12cm .则其内切圆的半径为______。2cmDCEO如图:从⊙O外的定点P作⊙O
的两条切线,分别切⊙O于点A
和B,
⑵ ∠DOE的大小是定值 在弧AB上任取一点C,过
点C作⊙O的切线,分别交PA、
PB于点D、E。试证:⑴ △PDE的周长
是定值(PA+PB)(∠AOB/2)若∠P=40°,你能说出∠DOE的度数吗?PABOPABCO达 标 检 测1、填空:已知⊙O的半径为3cm,点P和圆心O的距离为6cm,经过点P有⊙ O的两条切线,则切线长为______cm。这两条切线的夹角为_____度。2、证明题:已知:如图,P为⊙ O外一点,PA、PB 为⊙ O 的切线,A和B是切点,BC是直径 求证:AC∥OP
60证明:连结AB
∵PA、PB分别切⊙O于A、B
∴PA=PB ∠OPA=∠OPB
∴OP⊥AB
又∵BC为⊙O的直径
∴AC⊥AB
∴AC∥OP
2、切线长定理的内容是什么?
3、这个定理是怎样证明的?切 线 长 定 理∵PA、PB分别切⊙O于A、B∴PA = PB∠OPA=∠OPB。PABOC如图:PA、PB是⊙O的两条切线,A、B为切点。思考:由切线长定理可以得出哪些结论?
PA与PB关于直线OP对称,
∠APB+∠AOB=180°
OP平分∠AOB、弦AB、弧AB
OP垂直于AB作一个圆,使它与∠ABC的两边相切与一个角两边都相切的圆的圆心在这个角的角平分线上动手I有一块三角形铁皮ABC,现要剪出一个最大的圆,怎么剪?圆心是三角形
三条角平分线
的交点 和三角形三边都相切的圆叫做三角形的内切圆,内切圆的圆心叫做三角形的内心,这个三角形叫做圆外切三角形有关概念⊙I是△ABC的 ,
点I是△ABC的 ,
△ABC是⊙I的 。内切圆内心外切三角形归纳内心的性质1、内心是三角形内切圆的圆心
2、内心到各边的距离相等
3、内心是各角平分线的交点探究与应用在△ABC中,∠A=70°
①若O是△ABC的外心,则∠BOC= ;
②若O是△ABC的内心,则∠BOC= 。
140°125°2、已知:在△ABC中,AB=14,BC=9,AC=13,它的内切圆分别和BC、AC、AB切于点D、E、F,求AF、BD和CE的长。探究与发现1、如图,哪些线段相等?设△ABC的BC=a,CA=b,AB=c,内切圆I和BC、AC、AB分别相切于点D、E、F分析:设 AF=x,BD=y,CE=z 例:直角三角形的两直角边分别是5cm, 12cm .则其内切圆的半径为______。2cmDCEO如图:从⊙O外的定点P作⊙O
的两条切线,分别切⊙O于点A
和B,
⑵ ∠DOE的大小是定值 在弧AB上任取一点C,过
点C作⊙O的切线,分别交PA、
PB于点D、E。试证:⑴ △PDE的周长
是定值(PA+PB)(∠AOB/2)若∠P=40°,你能说出∠DOE的度数吗?PABOPABCO达 标 检 测1、填空:已知⊙O的半径为3cm,点P和圆心O的距离为6cm,经过点P有⊙ O的两条切线,则切线长为______cm。这两条切线的夹角为_____度。2、证明题:已知:如图,P为⊙ O外一点,PA、PB 为⊙ O 的切线,A和B是切点,BC是直径 求证:AC∥OP
60证明:连结AB
∵PA、PB分别切⊙O于A、B
∴PA=PB ∠OPA=∠OPB
∴OP⊥AB
又∵BC为⊙O的直径
∴AC⊥AB
∴AC∥OP
同课章节目录
