圆的性质[上学期]

2版
人教九年级上第二十四章《圆》第一期随堂练习及快乐周周练
随堂练习一
一、练习内容： 圆、垂直于弦的直径
二、练习目标：
1.了解圆的概念，及半径、直径、弦、弧、半圆、弓形、优弧、劣弧、等弧等概念。
2.掌握垂径定理及其推论，并会运用它们进行计算和证明、作图等。
3、掌握“常作垂直于弦的直径”这条辅助线及其转化作用。
三、练习题
（1） 仔细看，选一选
1.下列结论中，正确的是（ ）.
A.圆的大小是由圆心和半径确定的
B.等弧就是长度相等的两条弧
C.圆是轴对称图形，但它不是中心对称图形
D.平分弦的直线垂直于弦
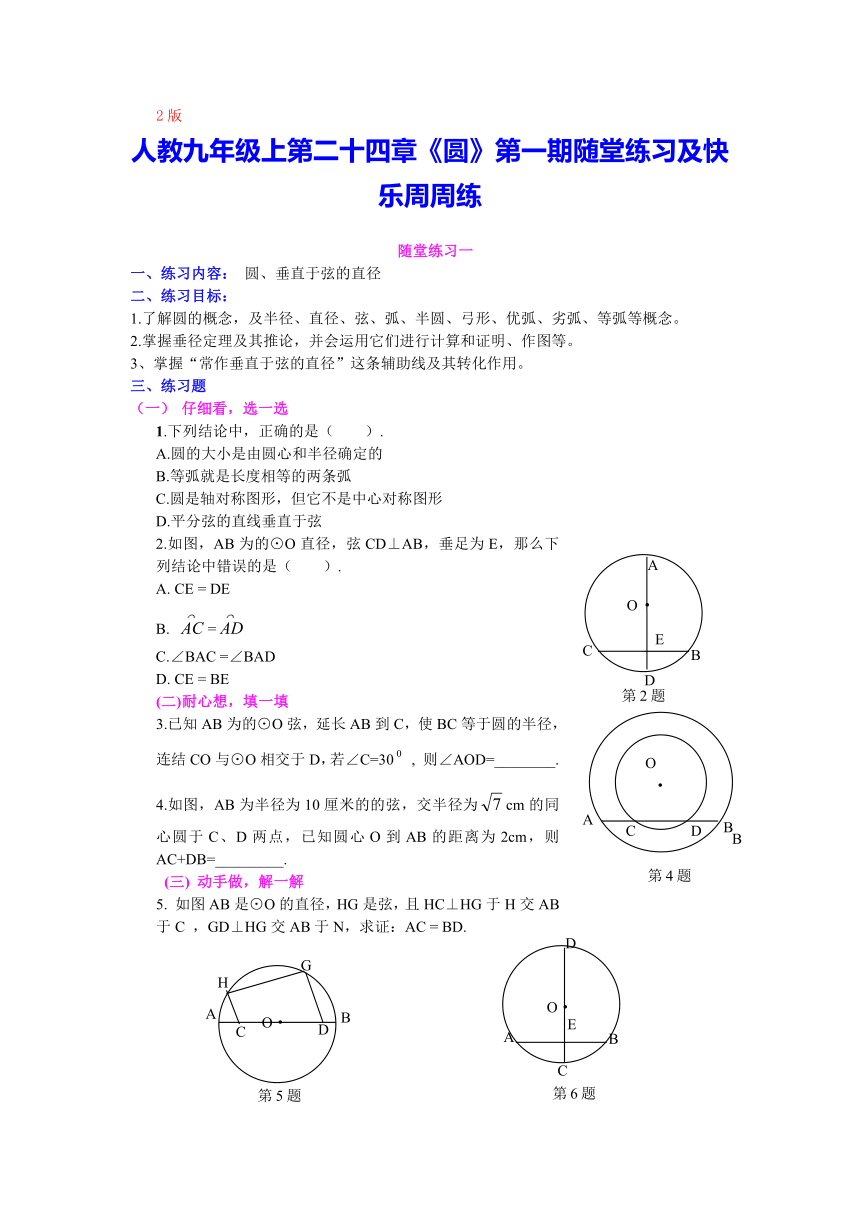
2.如图，AB为的⊙O直径，弦CD⊥AB，垂足为E，那么下列结论中错误的是（ ）.
A. CE = DE
B. =
C.∠BAC =∠BAD
D. CE = BE
(2) 耐心想，填一填
3.已知AB为的⊙O弦，延长AB到C，使BC等于圆的半径，连结CO与⊙O相交于D，若∠C=30 , 则∠AOD=________.
4.如图，AB为半径为10厘米的的弦，交半径为cm的同心圆于C、D两点，已知圆心O到AB的距离为2cm，则AC+DB=_________.
(三) 动手做，解一解
5. 如图AB是⊙O的直径，HG是弦，且HC⊥HG于H交AB于C ，GD⊥HG交AB于N，求证：AC = BD.
6、如图，CD为⊙O的直径，弦AB⊥CD于点E ，CE= 1 , AB=10 , 求CD的长.
参考答案
一、选择题
1. A 2. D
二、填空题
3. 90 4. 8- 2
三、解答题
5.过O作OE⊥HG垂足为E,则由垂径定理可得HE=GE, ∴OE为梯形CDGH的中位线，
∴OC=OD,又∵OA=0B， ∴AC=BD
6.连结OA，设CD=2r，在△AOE中，OA=CE+AE, ∴r=(r-1) +25,解得r =13,
∴CD=26.
随堂练习二
一、练习内容：弧、弦、圆心角；圆周角
二、练习目标：
1. 了解圆的旋转不变性和圆是中心对称图形.
2.熟练掌握圆心角、弦、弧、弦心距之间的相等关系.
3.掌握圆周角的概念及其定理和推论.
三、练习题
（一）仔细看，选一选
1.如果两个圆心角相等，那么（ ）.
A. 这两个圆心角所对的弧相等
B. 这两个圆心角所对的弦相等
C. 这两个圆心角所对的弦的弦心距相等
D. 这两个圆心角所对的弧的度数相等
2.半径为R的圆中，有一弦分圆周成1：2两部分，则弦所对的圆周角的度数是（ ）.
A. 60 B. 120 C.60或120 D.30或150
（二）耐心想，填一填
3.在⊙O中，一条弦长等于这个圆的半径，则这条弦所对的圆心角为________
4.如图所示，在⊙O中，∠BOC=50, OC∥AB则∠BDC的度数为________。
(三) 动手做，解一解
.5.如图所示，已知在△ABC中，∠ACB=90,∠B=35,，以C为圆心，以CA为半径的圆交AB于D点，求的度数.
6.如图，AB,AC是⊙O的两条弦，延长CA到D，使AD=AB，
∠ADB=40,求∠BOC的度数.
参考答案
一、选择题
1. D 2.C
二、填空题
3. 60 4. 75
三、解答题
5. 70, 提示：∵∠B=35, ∠BCA=90, ∴∠A=55,连结CD,CD=CA, ∠A=∠CDA=55.故∠CDA=70，∴的度数为70
6. 160, 提示: ∵AD=AB, ∴∠ADB=∠ABD=40,∴∠BAC=80, ∴∠B0C= 2∠BAC=160
随堂练习三
一、练习内容：点和圆的位置关系；直线和圆的位置关系.
二、练习目标：
1. 掌握点与圆的三种位置关系及其判别方法.
2. 掌握直线与圆的三种位置关系.
3. 熟练掌握圆的切线的判定定理和性质定理及两个推论，并会灵活运用它们进行证明、计算和画图。
4. 理解切线长的概念，熟练掌握并灵活运用切线长定理。
三、练习题
（一）仔细看，选一选
1.已知⊙O的半径r =2cm，直线l与⊙O的圆心的距离d= cm，则直线l与圆的位置关系是( ).
A. 相离 B. 相切 C. 相交 D. 不确定
2.在△ABC中，∠ABC=80, ∠ACB=40,O是△ABC的有
内心，则∠BOC为（ ）
A. 100 B. 90 C.120 D.80
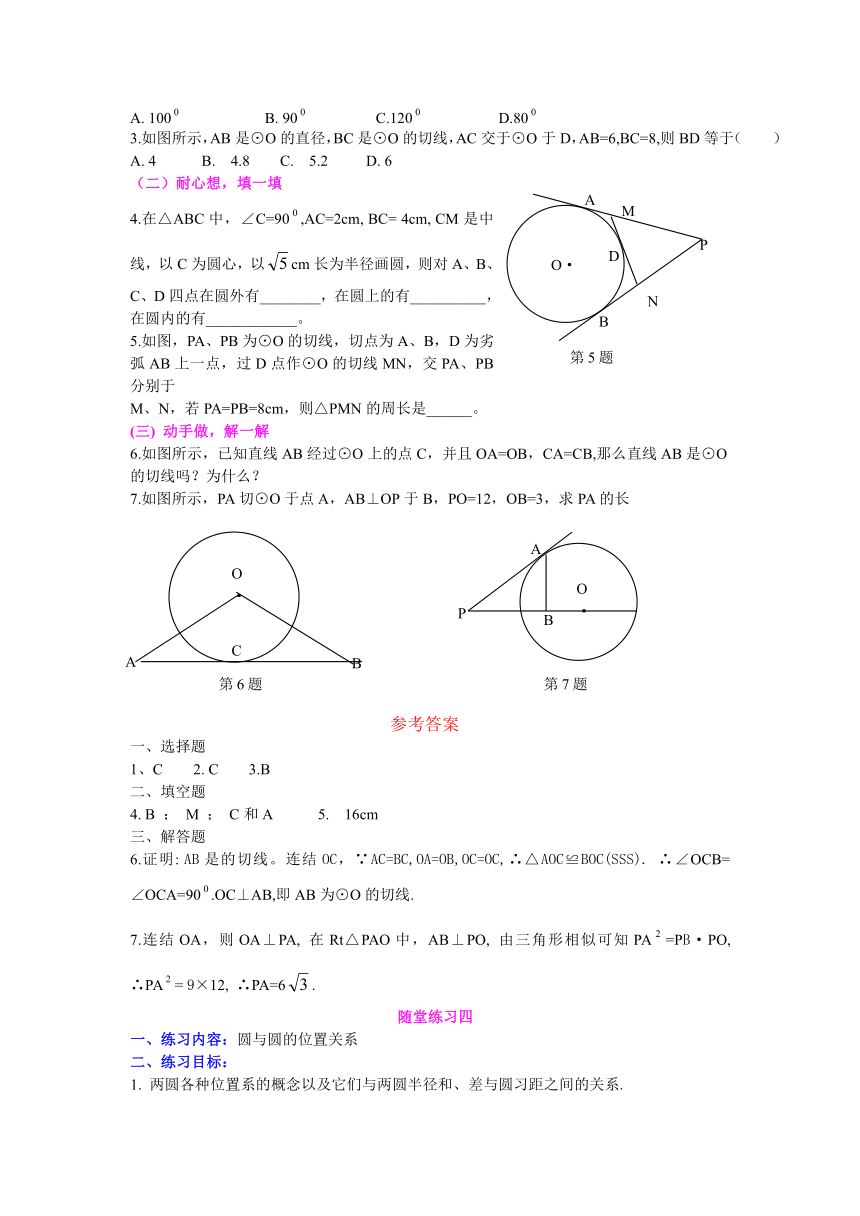
3.如图所示，AB是⊙O的直径，BC是⊙O的切线，AC交于⊙O于D，AB=6,BC=8,则BD等于（ ）
A. 4 B. 4.8 C. 5.2 D. 6
（二）耐心想，填一填
4.在△ABC中，∠C=90,AC=2cm, BC= 4cm, CM是中线，以C为圆心，以cm长为半径画圆，则对A、B、C、D四点在圆外有________，在圆上的有__________，在圆内的有____________。
5.如图，PA、PB为⊙O的切线，切点为A、B，D为劣弧AB上一点，过D点作⊙O的切线MN，交PA、PB分别于
M、N，若PA=PB=8cm，则△PMN的周长是______。
(三) 动手做，解一解
6.如图所示，已知直线AB经过⊙O上的点C，并且OA=OB，CA=CB,那么直线AB是⊙O的切线吗？为什么？
7.如图所示，PA切⊙O于点A，AB⊥OP于B，PO=12，OB=3，求PA的长
参考答案
一、选择题
1、C 2. C 3.B
二、填空题
4. B ； M ； C和A 5. 16cm
三、解答题
6.证明: AB是的切线。连结OC，∵AC=BC,OA=OB,OC=OC,∴△AOC≌BOC(SSS). ∴∠OCB= ∠OCA=90.OC⊥AB,即AB为⊙O的切线.
7.连结OA，则OA⊥PA, 在Rt△PAO中，AB⊥PO, 由三角形相似可知PA=PB·PO, ∴PA= 9×12, ∴PA=6.
随堂练习四
一、练习内容：圆与圆的位置关系
二、练习目标：
1. 两圆各种位置系的概念以及它们与两圆半径和、差与圆习距之间的关系.
2. 两圆位置关系的图形判别及数量法判定.
3. 熟练掌握相切两圆和相交两圆的性质.
三、练习题
（一）仔细看，选一选
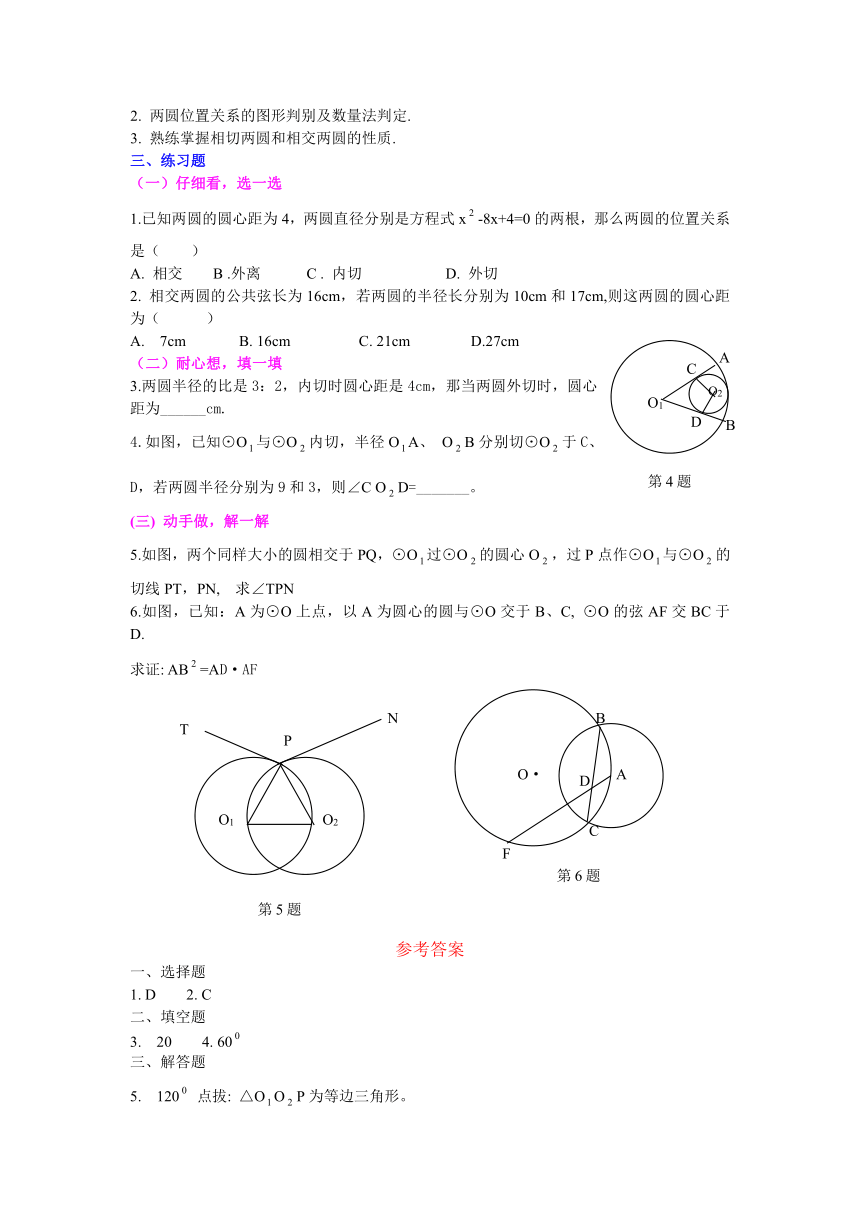
1.已知两圆的圆心距为4，两圆直径分别是方程式x-8x+4=0的两根，那么两圆的位置关系是（ ）
A. 相交 B .外离 C . 内切 D. 外切
2. 相交两圆的公共弦长为16cm，若两圆的半径长分别为10cm和17cm,则这两圆的圆心距为（ ）
A. 7cm B. 16cm C. 21cm D.27cm
（二）耐心想，填一填
3.两圆半径的比是3：2，内切时圆心距是4cm，那当两圆外切时，圆心距为______cm.
4.如图，已知⊙O与⊙O内切，半径OA、 OB分别切⊙O于C、D，若两圆半径分别为9和3，则∠C OD=_______。
(三) 动手做，解一解
5.如图，两个同样大小的圆相交于PQ，⊙O过⊙O的圆心O，过P点作⊙O与⊙O的切线PT，PN, 求∠TPN
6.如图，已知：A为⊙O上点，以A为圆心的圆与⊙O交于B、C, ⊙O的弦AF交BC于D.
求证: AB=AD·AF
参考答案
一、选择题
1. D 2. C
二、填空题
3. 20 4. 60
三、解答题
5. 120 点拔: △OOP为等边三角形。
6.证明：连结BF、AB、AC, ∵AC=AB, ∴=. ∴∠BFA=∠CBA, 又∵∠BAD=∠FAB, ∴△BAD～△FAB, ∴= ，即：AB = AD·AF
3版
快乐周周练一
[每周必读]
本周主要学习了(1)垂径定理、弦、弧、圆心角之间的关系、圆周角定理及其推论；(2)点与圆的位置关系、直线与圆的位置关系、圆与圆的位置关系、切线的性质和判定等有关问题的关键，希望同学们要掌握好这些，为以后的学习奠定基础。
（一）仔细看，选一选（每小题3分,共24分）
1.下列结论正确的是（ ）
A、长度相等的两条弧是等弧
B、相等的圆心角所对的弧相等
C、圆是轴对称图形
D、平分弦的直线垂直于弦
2、如图1，⊙O的半径为4cm，C是的中点，
半径OC交弦AB于D，OD=2cm，则弦AB长
为（ ）
A、2cm B、3cm C、2cm D、4cm
3、如图2，⊙O的弦AB垂直于直径MN，C为垂足，
若OA=5cm，下面四个结论中可能正确的是（ ）
A、AB=12cm B、OC=6cm
C、MN=8cm D、AC=2.5cm
4、在半径为4的⊙O中，有长为4的的弦AB，则下弦所对的圆心角∠AOB
的度数为（ ）
A、600 B、900 C、1200 D、1500
5、Rt△ABC中，斜边AB=10，以AB的中点D为圆心，5为半径作⊙O，则A、
B、C三点与⊙O的位置关系是（ ）
A、A、B、C三点都在⊙O上 B、A、B、C三点都在⊙O内
C、A、B、C三点都有⊙O外 D、以上都不对
6、下列命题正确的个数 （ ）
①三角形的内心一定在三角形的内部，外心在三角形的外部
②三角形的内心是三角形三边中垂线的交点，所以它到三角形三个顶点的距离相等
③三角形的内心是三角形三个内角平分线的交点，它到三角形三边的距离相等
④等边三角形的内心和外心是同一个点
A、1个 B、2个 C、3个 D、4个
7、已知两的圆心距为6，两圆的直径公别是方程x2-6x+1=0的两根，那么两圆的位置
关系是（ ）
A、相交 B、外离 C、内切 D、外切
8、已知相交两圆的半径分别为5和8，那么这两圆的圆心距d的取值范围是（ ）
A、 d＞3 B、d＜3 C、3＜d＜13 D、d=3或d=13
（二）耐心想，填一填（每小题3分,共24分）
9、等腰直角三角形ABC的腰长为5，D是斜边上AB的中点，则以D为圆心、---------------
为半径的圆经过A、B、C；以D为圆心，2.5为半径的圆与直线-------------相切，当半径为
-------------------时，⊙O与AC、BC、AB都相切。
2、在⊙O的直径CB的延长线上取一点A，AP切⊙O于P，且∠APB=300，AB=
则CP=---------------------------------.
3、已知∠AOB=300，M为OB上一点，且OM=3，以M为圆心，以---------------为半径的
圆与OA相切。
4、在Rt△ABC中，∠C=900，AC=3，BC=4，若以C为圆心，R为半径的圆与斜边AB
只有一个公共交点，则R的取值范围是--------------------------------------------------
5、如图3，AB切⊙O于C，AO交⊙O于D，AO的延长线交⊙O于E，若∠A=x，则
∠ECB=--------------------------------------
6、两圆的半径之比为5：3，外切时两圆的圆心距为32，那么两圆内切两圆的圆心距
是--------------------------------------
7、⊙O1与⊙O2外切于点T，过T的直线分别交两圆于A、B，若两圆的半径分别为6
和9，则TA：TB=----------------------------
8、矩形ABCD中，AB=5，BC=12，如果分别以A、C为圆心的两圆外切，点在⊙C内，
点B在⊙C外，那么⊙A的半径的取值范围是----------------------.
（三）动手做，解一解（20分）
17.如图4，矩形ABCD的一边经过⊙O的圆心，E、L、F、H分别是AB、CD与⊙O的交点，若AE=3，AD=4，DF=5，求 ⊙O的半径（10分）
18. 如图5，AB是 ⊙O的直径，⊙O过BC的中点D，DE⊥AC于E。
求证：DE是⊙O的切线（10分）
四、创新应用（共12分）
19. 如图6，OM、OM为相交300的角两条公路，在OM上距O点80米的A处有一所小学，一拖拉机以每小时36公里的速度从O点向N点行驶，若它与学校的距离不足50米时会对学校产生影响，试问拖拉机对学校的影响时间多长？
20．（15分）直线PE、PF相交于P，交⊙O于A、B、C、D。
（1）若在⊙O外，且AB=CD，如图7，
求证：PO平分∠EPF
（2）若点P在⊙O内，其它条件不变，（AB=CD）不变，
①中的结论还成立吗？
（3）若点P在⊙O内，过P点作弦MN，且P为MN的中点，如图8，
∠BPN=∠DPN，则选----------------------
① ②BC=AD ③AB=CD
从①②③中任选一个合适的将题目补充完整，并完成证明
五、探索拓展（每小题12分，共20分）
21．如图 9，在三角形ABC中，∠BAC=900，AB=AC=，圆A的半径为1，若点O在B上，运动，（与B、C点不重合），设BO=x，△ABC的面积为y。
（1）求y关于x的函数解析式
（2）以点O为圆心，BO长为半径作⊙O，求当⊙O与⊙A相切
时，△ABC的面积
22．已知AB是 ⊙O的直径，P为AB延长线上的一动点，过点P作⊙O的切线，设切点为C。
（1）当点P在AB的延长线上的位置如图10所示时，连结AC，作∠APC的平分线，交AC于点D，请测量出∠CPD的度数
（2）当点P在AB的延长线上的位置如图11所示时，连结AC，请分别在这两个圆中用尺规作∠APC的角平线，（不写作法，保留作图痕迹），设此角平分线交AC于点D，然后在这两个圆中测量出∠COP的度数
猜想∠CPD的度数是否随点P在AB延长线的位置上的变化而变化？请对你的猜想加以证明 （13分）
答案
1、A 2、D 3、D 4、C 5、A 6、B 7、D 8、C
9、cm AC和BC ＜ r ≤ 10、3 11、1.5 12、r=
或3＜r≤4 13、450+ 14、8 15、2∶3 16、1＜r＜8
17、 5.连结OF，作OG⊥FH，垂足为G。设OF=r，则OG=4，
FG=r+3-5=r-2，又OF2=OG2+FG2，∴r2=16+（r-2）2，解得 r=5
18、证明：连结OD
∵BD=DC，OA=OB
∴OD∥AC
又∵DE⊥AC
∴OD⊥DE
故DE是⊙O的切线
19、小时，解：作AD⊥ON，则AD=40＜50，∴不会受影响，设从B点开始受
影响到C点结束，∴AB=AC=50，AD=40，∴BD=DC=30，∴影响时间为小时。
20、（1）证明：过点O作OM⊥AB，ON⊥DC，垂足分别为M、N，∵AB=CD
∴OM=ON ∴OP平分∠EPF
（2）若点P在⊙O内，其它条件不变，（1）中的结论仍然成立
（3） ③AB=CD 证明：连OP，过点O作OG⊥CD，OH⊥AB，
垂足分别为G、H ∵P是MN的中点 ∴OP⊥MN，∴∠OPM=∠OPN=900。
即PO平分∠DPB， ∴OG=OH ∴ AB=CD
21、（1）过点A作AH⊥BC，于点H，∵∠BAC=900，AB=AC=，∴BC=4，AH==2，
S△AOC=4-x 即 y=-x+4 （0＜x＜4）
（2）当点O与点H重合时，⊙O与⊙A相交，不合题；
当点O与点H不重合时，在直角三角形AOH中，AO2=AH2+OH2=x2-4x+8
①当圆O与圆A外切时 （x+1）2=x2-4x+8 解得x=，此时三角形的面积为
②当圆O与圆A内切时，（x-1）2=x2-4x+8 x= 此时三角形的面积为
22、（1）∠CDP=450 （2）∠CDP=450 猜想：∠CDP=450为定值
证明：∵PC为⊙O的切线 ∴∠PCB=∠A ∵∠CDE=∠A+∠APD
CED=∠DPC+∠BCP ∠DPC=∠APD ∴∠CDE=∠CED 又∠ACB=900
∴∠CDE=450
O
·
A
E
C
D
第2题
A
B
C
D
B
O ·
第4题
A
B
C
D
B
G
H
O·
第5题
A
B
C
D
E
O·
第6题
A
B
D
O
C
第4题
A
C
B
D
第5题
A
C
D
B
O
第6题
A
B
D
C
O
第3题
B
N
P
D
M
A
O·
第5题
B
C
A
C
A
O·
第6题
第7题
A
B
P
O·
D
O11
C
A
B
O2
第4题
第5题
第6题
P
T
N
O11
O2
B
C
D
A
F
O·
B
（图1）
O
D
B
（图2）
A
O
C
B
A
C
D
（图4）
L
E
.O
F
H
A
D
（图5）
C
E
B
·
O
A
（图6）
O
N
A
A
P
C
B
H
( 图7)
·O
D
D
M
N
B
O
A
（图8）
C
B
O
C
（图9）
A
B
O
A
P
C
（图12）
B
A
P
C
（图11）
B
C
P
A
O
（图10）
O
O
O