圆心角[上学期]

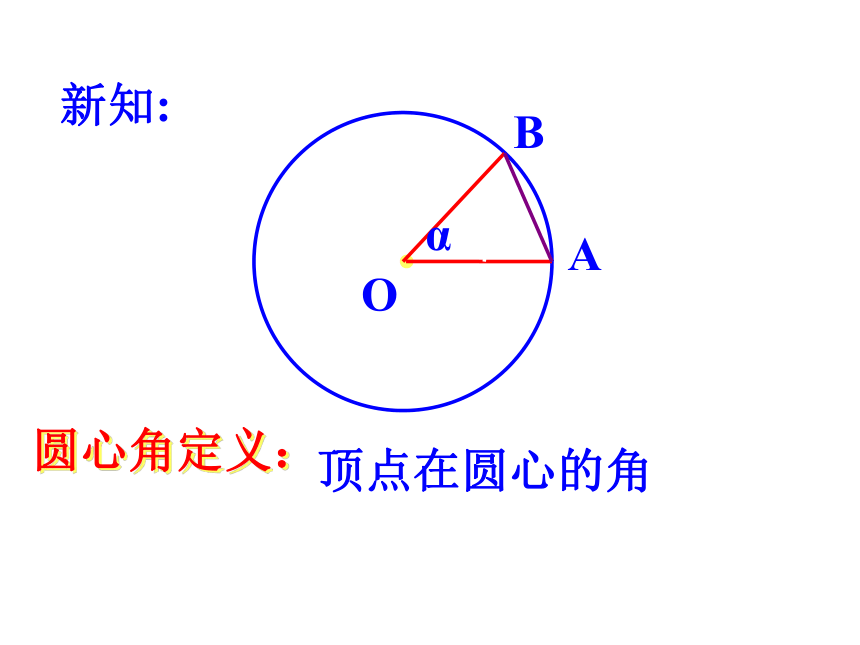
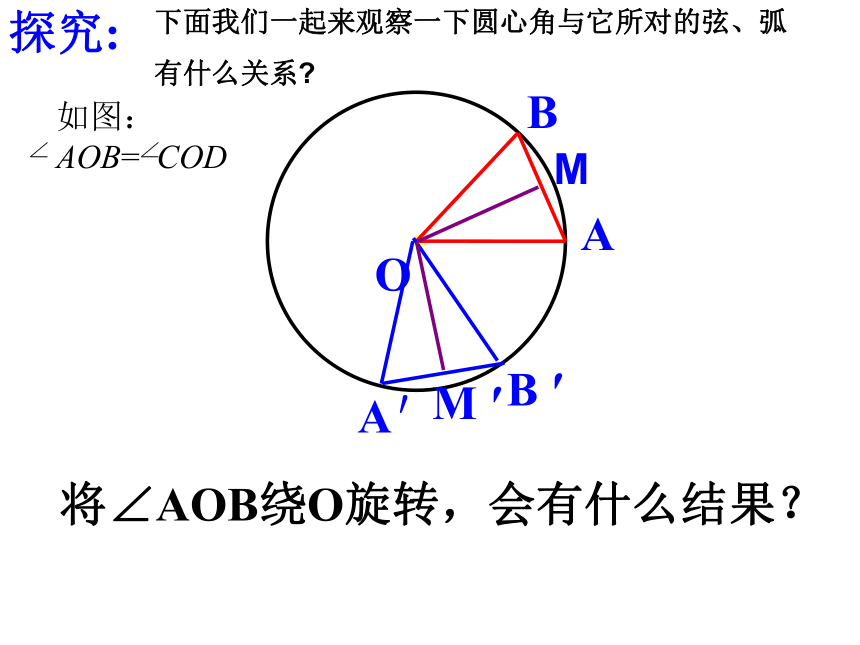
课件17张PPT。欢迎您进入多媒体教学的世界圆心角.弧.弦.弦心距之间的关系圆是一个中心对称图形圆有旋转不变性:旋转任意角度都能与自身重合.新知:αAB圆心角定义：顶点在圆心的角探究:αABA′B ′α将∠AOB绕O旋转，会有什么结果？下面我们一起来观察一下圆心角与它所对的弦、弧
有什么关系?MM ′新知: αABA′B ′α在同圆或等圆中，相等的圆心角所对
的弧相等，所对的弦相等，所对的弦
的弦心距相等。圆心角定理(1) 圆心角(2) 弧(3) 弦(4) 弦心距MM ′αABA′B ′α(1) 圆心角(2) 弧(3) 弦(4) 弦心距MM ′等对等定理整体理解：知一得三练习 ABCD1、O1和O2是等圆，AD‖O1O2，下列
正确的是( )
A AB= CD且AB≠CD
B AB= CD且AB≠CD
C AB= CD且AB= CD
D 以上都不对例:例1 如图，点O是∠EPF角平分线上的
一点，以O为圆心的圆和角的两边分别
交于点A、B和C、D。
求证：AB= CD。ABPCDEFMN练习2、如图，⊙O中两条相等的弦AB、
CD分别延长到E、F，使BE= DF。
求证：EF的垂直平分线必经过点O。ABCDEFMN∵把圆心角等分成功360份,则每一份的圆心角是1o.同时整个圆也被分成了360份.则每一份这样的弧叫做1o的弧.这样,1o的圆心角对着1o的弧,
1o的弧对着1o的圆心角.
n o的圆心角对着no的弧,
n o的弧对着no的圆心角.性质:弧的度数和它所对圆心角的度数相等.小结弧的度数圆心角定理的应用圆心角定理圆心角的定义学习要点提要
回到主界面学生练习圆的旋转不变性Bye-by!