新人教版九年级上册24.1.3
文档属性
| 名称 | 新人教版九年级上册24.1.3 |

|
|
| 格式 | rar | ||
| 文件大小 | 54.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-10-16 00:00:00 | ||
图片预览




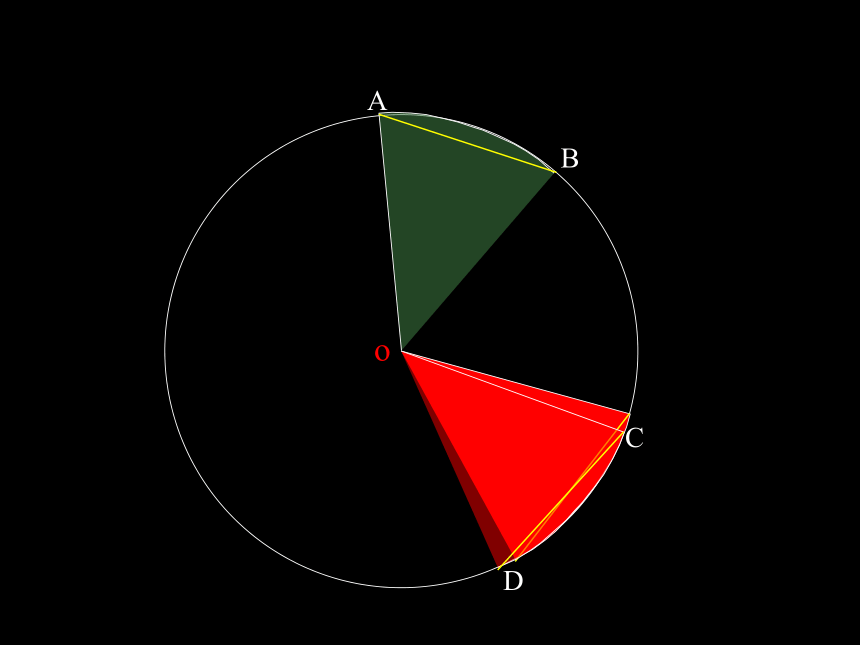
文档简介
课件42张PPT。1、了解圆的旋转不变性。
2、理解圆心角、弦心距的概念。
3、掌握圆心角、弧、弦、弦心距之间的关系学习目标圆是轴对称图形,圆的对称轴是任意一条经过圆
心的直线,它有无数条对称轴.圆也是中心对称图形,它的对称中心就是圆心.用旋转的方法可以得到:一个圆绕着它的圆心旋转任意一个角度,都能与原来的图形重合.这是圆特有的一个性质:圆的旋转不变性
利用旋转不变性来研究另一个重要定理复习回忆利用这个性质我们得出了垂经定理,圆心角、弧、弦、弦心距之间的关系 过点O作弦AB的垂线, 垂足
为M,AB 1.有关概念: 顶点在圆心的角,叫圆心角,
如 , 所对的弦为AB; 则垂线段OM的长度,即圆
心到弦的距离,叫弦心距 , 图1
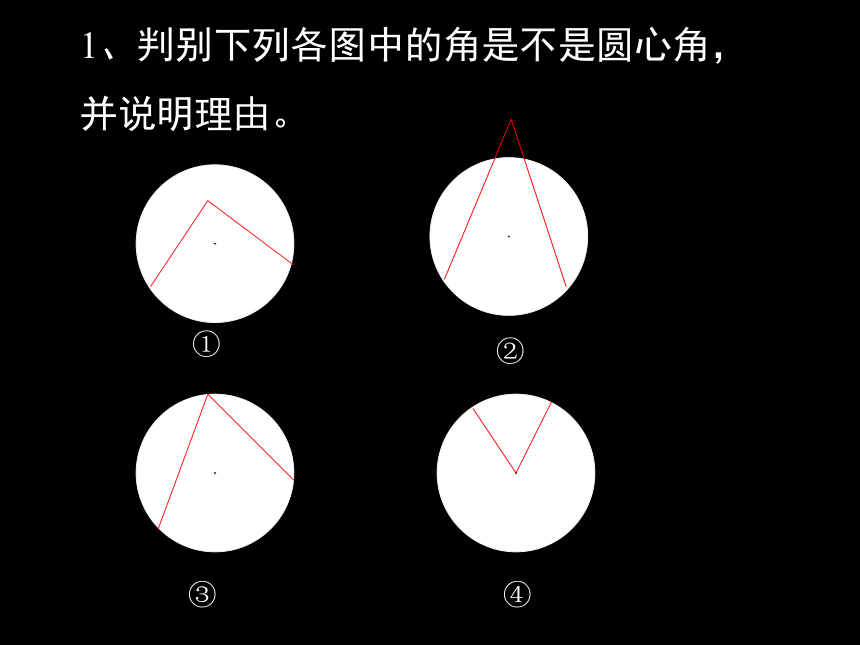
中,OM为AB弦的弦心距。1、判别下列各图中的角是不是圆心角,
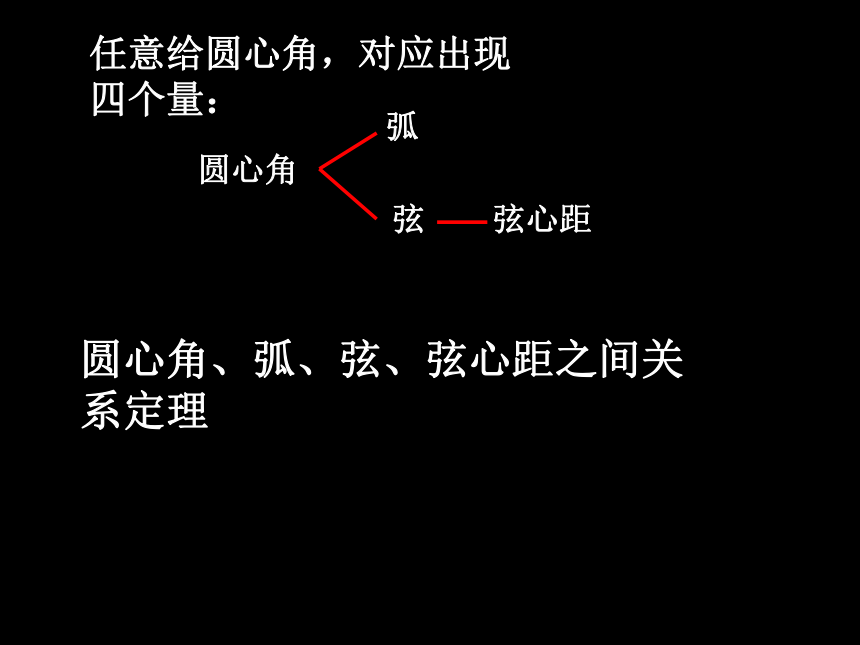
并说明理由。①②③④任意给圆心角,对应出现
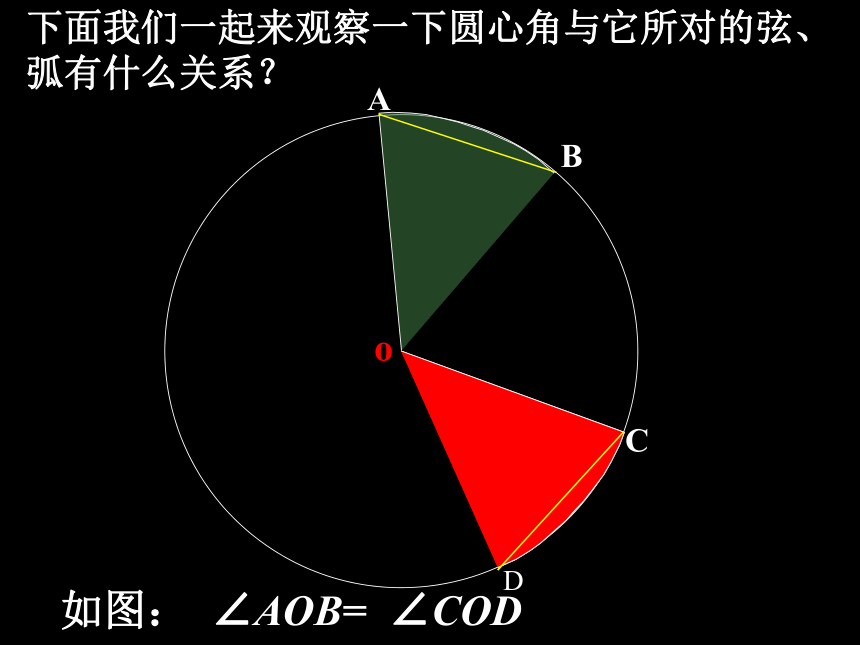
四个量:圆心角弧弦 弦心距圆心角、弧、弦、弦心距之间关系定理ABCDo下面我们一起来观察一下圆心角与它所对的弦、弧有什么关系?ABCDoABCDoABCDoABCDoABCDoABCDoABCDo??ABCDoABCDoABCDoABCDoABCDoABCDoABCDoABCDoABCDoABCDoABCDoABCDo??ABCDo?????下面我们一起来观察一下圆心角与它所对的弦、弧有什么关系?下面我们一起来观察一下圆心角与它所对的弦、弧有什么关系? ∵∠AOB= ∠COD,
∴半径OB与OA重合,
∴ 点A与点C重合,点B与点D重合。
∴ AB=CD,
根据圆的性质,AB与CD重合。
此时,称作 两条圆弧相等。
记作:“AB=CD” ⌒⌒⌒⌒定理:在同圆或等圆中,相等的圆心角所对弧相等,所对的弦相等,所对的弦的弦心距相等。 圆心角, 弧,弦,弦心距之间的关系定理在同圆或等圆中,相等的圆心角所对的弧相等所对的弦相等,所对的弦的弦心距相等.由条件:
①∠AOB=∠A′O′B′③AB=A′B′④ OD=O′D′拓展与深化在同圆或等圆中,如果轮换下面四组条件:
①两个圆心角,②两条弧,③两条弦,④两条弦心距,你能得出什么结论?与同伴交流你的想法和理由.如由条件:③AB=A′B′④ OD=O′D′①∠AOB=∠A′O′B′推论在同圆或等圆中,如果①两个圆心角,②两条弧,③两条弦,④两条弦心距中,有一组量相等,那么它们所对应的其余各组量都分别相等.如由条件:③AB=A′B′④ OD=O′D′①∠AOB=∠A′O′B′条件结论在同圆或等圆中
如果圆心角相等那么圆心角所对的弧相等圆心角所对的弦相等圆心角所对的弦的
弦心距相等推论:(圆心角定理的逆定理)
在同圆或等圆中,如果两个圆心角、两条弧、两条弦或两条弦的弦心距中有一组量相等,那么它们所对应的其余的各组量都分别相等。OAB下面的说法正确吗?为什么?
如图,因为 ,根据圆心角、弧、弦、
弦心距的关系定理可知: ⌒⌒例题与练习如图:已知OA.OB是⊙O中的两条半径,且OA⊥OB,D是弧AB上的一点,AD的延长线交OB延长线于C。已知C=250,求圆心角∠DOB的度数,CODBA已知AB是⊙O的直径,M.N是AO.BO的中点。CM⊥AB,DN⊥AB,分别与圆交于C.D点。求证:弧AC=弧BDADCNMB
2、理解圆心角、弦心距的概念。
3、掌握圆心角、弧、弦、弦心距之间的关系学习目标圆是轴对称图形,圆的对称轴是任意一条经过圆
心的直线,它有无数条对称轴.圆也是中心对称图形,它的对称中心就是圆心.用旋转的方法可以得到:一个圆绕着它的圆心旋转任意一个角度,都能与原来的图形重合.这是圆特有的一个性质:圆的旋转不变性
利用旋转不变性来研究另一个重要定理复习回忆利用这个性质我们得出了垂经定理,圆心角、弧、弦、弦心距之间的关系 过点O作弦AB的垂线, 垂足
为M,AB 1.有关概念: 顶点在圆心的角,叫圆心角,
如 , 所对的弦为AB; 则垂线段OM的长度,即圆
心到弦的距离,叫弦心距 , 图1
中,OM为AB弦的弦心距。1、判别下列各图中的角是不是圆心角,
并说明理由。①②③④任意给圆心角,对应出现
四个量:圆心角弧弦 弦心距圆心角、弧、弦、弦心距之间关系定理ABCDo下面我们一起来观察一下圆心角与它所对的弦、弧有什么关系?ABCDoABCDoABCDoABCDoABCDoABCDoABCDo??ABCDoABCDoABCDoABCDoABCDoABCDoABCDoABCDoABCDoABCDoABCDoABCDo??ABCDo?????下面我们一起来观察一下圆心角与它所对的弦、弧有什么关系?下面我们一起来观察一下圆心角与它所对的弦、弧有什么关系? ∵∠AOB= ∠COD,
∴半径OB与OA重合,
∴ 点A与点C重合,点B与点D重合。
∴ AB=CD,
根据圆的性质,AB与CD重合。
此时,称作 两条圆弧相等。
记作:“AB=CD” ⌒⌒⌒⌒定理:在同圆或等圆中,相等的圆心角所对弧相等,所对的弦相等,所对的弦的弦心距相等。 圆心角, 弧,弦,弦心距之间的关系定理在同圆或等圆中,相等的圆心角所对的弧相等所对的弦相等,所对的弦的弦心距相等.由条件:
①∠AOB=∠A′O′B′③AB=A′B′④ OD=O′D′拓展与深化在同圆或等圆中,如果轮换下面四组条件:
①两个圆心角,②两条弧,③两条弦,④两条弦心距,你能得出什么结论?与同伴交流你的想法和理由.如由条件:③AB=A′B′④ OD=O′D′①∠AOB=∠A′O′B′推论在同圆或等圆中,如果①两个圆心角,②两条弧,③两条弦,④两条弦心距中,有一组量相等,那么它们所对应的其余各组量都分别相等.如由条件:③AB=A′B′④ OD=O′D′①∠AOB=∠A′O′B′条件结论在同圆或等圆中
如果圆心角相等那么圆心角所对的弧相等圆心角所对的弦相等圆心角所对的弦的
弦心距相等推论:(圆心角定理的逆定理)
在同圆或等圆中,如果两个圆心角、两条弧、两条弦或两条弦的弦心距中有一组量相等,那么它们所对应的其余的各组量都分别相等。OAB下面的说法正确吗?为什么?
如图,因为 ,根据圆心角、弧、弦、
弦心距的关系定理可知: ⌒⌒例题与练习如图:已知OA.OB是⊙O中的两条半径,且OA⊥OB,D是弧AB上的一点,AD的延长线交OB延长线于C。已知C=250,求圆心角∠DOB的度数,CODBA已知AB是⊙O的直径,M.N是AO.BO的中点。CM⊥AB,DN⊥AB,分别与圆交于C.D点。求证:弧AC=弧BDADCNMB
同课章节目录
