新人教版九年级上册24.2.1点与圆的位置关系课件PPT[上学期]
文档属性
| 名称 | 新人教版九年级上册24.2.1点与圆的位置关系课件PPT[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 395.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-10-16 19:36:00 | ||
图片预览







文档简介
课件28张PPT。点与圆
的位置关系外语学校 liudeguang如图:是射击靶的示意图,你知道击中靶上不同位置的成绩是如何计算的吗????
靶上有圆,这些圆圆心相同,半径不同,称为同心圆。击中的位置可以看作一些点,点的不同位置决定了环数
..........观察图形,
这些点与圆有哪些位置关系? ..........点与圆的位置关系有三种:
点在圆内,
点在圆上,
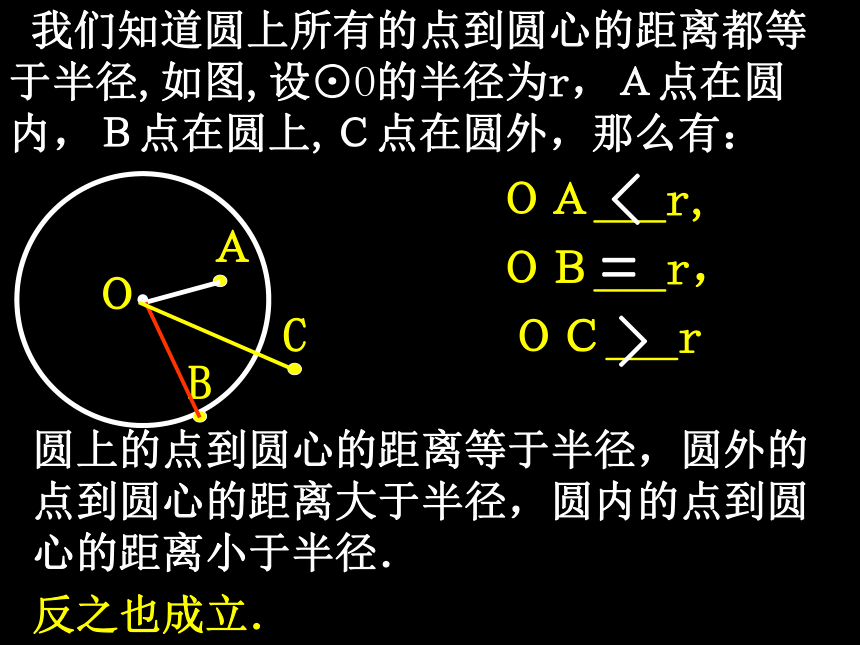
点在圆外思考:点与圆的位置与这些点与圆心的距离有何关系 我们知道圆上所有的点到圆心的距离都等于半径,如图,设⊙O的半径为r,A点在圆内,B点在圆上,C点在圆外,那么有:
OA___r,
OB___r,
OC___r=><O圆上的点到圆心的距离等于半径,圆外的点到圆心的距离大于半径,圆内的点到圆心的距离小于半径.
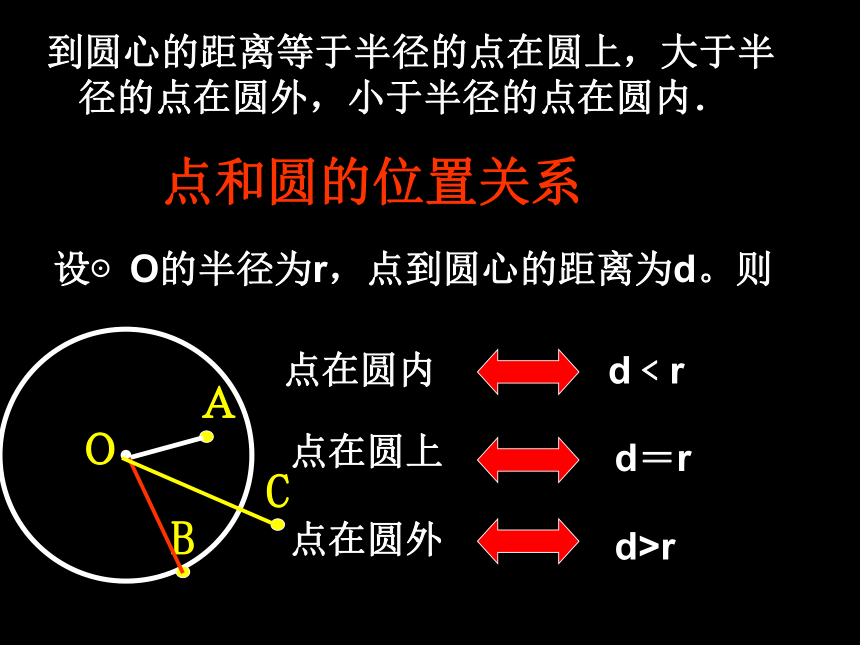
反之也成立. 到圆心的距离等于半径的点在圆上,大于半径的点在圆外,小于半径的点在圆内.设⊙O的半径为r,点到圆心的距离为d。则点和圆的位置关系点在圆内d﹤r点在圆上点在圆外d=rd>rO1.已知圆的半径等于5厘米,点到圆心的距离是:
①8厘米 ②4厘米 ③5厘米。
请你分别说出点与圆的位置关系。例题与练习
2、已知⊙O的半径为4,OP=3.4,则P在⊙O的 ( )。
3、已知 点P在 ⊙O的外部,OP=5,那么⊙O的半径r满足( )
4,已知⊙O的半径为5,M为ON的中点,当OM=3时,N点与⊙O的位置关系是N在⊙O的( )内部0﹤r ﹤5外部1.已知圆的半径等于5cm,根据下列点P到圆心的距离:(1)4cm;(2)5cm;(3)6cm;判定点P与圆的位置关系,并说明理由.
2.点A在以O为圆心,3cm为半径的⊙O内,则点A到圆心O的距离d的范围是
3.P为⊙O内与O不重合的一点,则下列说法正确的是( )
A.点P到⊙O上任一点的距离都小于⊙O的半径
B.⊙O上有两点到点P的距离等于⊙O的半径
C.⊙O上有两点到点P的距离最小
D.⊙O上有两点到点P的距离最大4.若⊙A的半径为5,点A的坐标为(3,4),点P的坐标为(5,8),则点P的位置为( )
A.在⊙A内 B.在⊙A上 C.在⊙A外 D.不确定
5.两个圆心为O的甲,乙两圆,半径分别为r1和r2,且r1<OA<r2,那么点A在( )
A.甲圆内 B.乙圆外 C.甲圆外,乙圆内 D.甲圆内,乙圆外
7.⊙O的半径为5,圆心O的坐标为(0,0),点P的坐标为(4,2),则点P与⊙O的位置关系( )
A.点P在⊙O内 B.点P在⊙O上
C.点P在⊙O外 D.点P在⊙O上或⊙O外
8.在△ABC中,∠C=90°,AC=BC=4cm,D是AB边的中点,以C为圆心,4cm长为半径作圆,则A.B,C,D四点中在圆内的有( )
A.1个 B.2个 C.3个 D.4个
9,一点和⊙O上的最近点距离为4cm,最远距离为9cm,则这圆的半径是 cm.5.Rt△ABC中,∠C=90°,CD⊥AB,AB=10,AC=6,以C点为圆心,6为半径画圆,则点A,B,D与圆的位置关系是怎样的?84.8....1,在Rt△ABC中,∠C=90°,AB=15cm,BC=10cm,以A为圆心,12cm为半径作圆,则点C与⊙A的位置关系是 .
2.⊙O的半径是3cm,P是⊙O内一点,PO=1cm,则点P到⊙O上各点的最小距离是 .
3.作图说明:到已知点A的距离大于或等于1cm,且小于或等于2cm的所有点组成的图形.
独立思考经过三点的圆A.过一点可以
画无数个圆.过一点作圆探究(1)
1、过一个已知点A如何作圆? 2、过点A所作圆的圆心在哪里?半径多大?可以作几个这样的圆?..AB过A,B两点有无数个圆,
圆心都在线段AB的中垂线上......过两点作圆探究(2)
1、过已知两点A、B如何作圆? 2、圆心A、B两点的距离怎样?能用式子表示吗?圆心在哪里?过点A、B两点的圆有几个? ...ABC.O1.不在同一条直线上的三个点确定一个圆分两种情形2.如果A,B,C三点在一条直线上,经过这三点你能画圆吗?ACB...经过三点作圆...ABC.O经过三角形三个顶点可以画一个圆,并且只能画一个.经过三角形三个顶点的圆叫做三角形的外接圆.三角形外接圆的圆心叫做这个三角形的外心;外心就是三角形三条边的垂直平分线的交点.这个三角形叫做这个圆的内接三角形.△ABC⊙O判断正误
1.经过三个点一定可以作圆.
2.任意一个三角形一定有一个外接圆.
3.任意一个圆一定有一内接三角形,并且只有一个内接三角形.
4.三角形的外心到三角形各个顶点的距离都相等.三角形的外心是否一定在三角形的内部?直角三角形外心是斜边AB的中点钝角三角形外心在△ABC的外面任意画一个直角三角形,然后再画这个三角形的
外接圆.如果是一个钝角三角形呢?
1.过点作圆
(1)过一点作圆
(2)过两点作圆
(3)过三点作圆
2.三角形的外接圆
今天我们学到了……练习判断题:(1)任意一个三角形一定有一个外接圆,
并且只有一个外接圆;(?? ) (2)任意一个圆一定有一个内接三角形,
并且只有一个内接三角形;(?? ) 随堂练习(3)三角形的外心到三角形各顶点的距
离相等.(?? )(4)三角形的外心在三角形的外部,
此三角形就是锐角三角形。( ) (5)过同一平面上的四点一定能做一个
圆。( ) 随堂练习随堂练习
1. 如果直角三角形的两条直角边分别是6,8,你能求出这个直角三角形的外接圆的半径吗?是多少?
2.在△ABC中,AB=AC=13,BC=10,试求这个三角形的外接圆的面积.应用 某一个城市在一块空地新建了三个居民小区,它们分别为A、B、C,且三个小区不在同一直线上,要想规划一所中学,使这所中学到三个小区的距离相等。请问同学们这所中学建在哪个位置?你怎么确定这个位置呢?●●●BAC三、思考题:
1.经过四个点是不是一定能作圆?所以经过四点不一定能作圆。4、2.思考题
①过三角形的三个顶点是否都可以作圆?为什么?
②一个三角形的外接圆有几个?一个圆的内接三角形有几个?为什么?
③三角形的外心有什么性质?它一定在三角形的内部吗?画图说明。3.想一想:
图中工具的CD边所在的直线恰好垂直平分
AB边,怎样用这个工具找出一个圆的圆心?
的位置关系外语学校 liudeguang如图:是射击靶的示意图,你知道击中靶上不同位置的成绩是如何计算的吗????
靶上有圆,这些圆圆心相同,半径不同,称为同心圆。击中的位置可以看作一些点,点的不同位置决定了环数
..........观察图形,
这些点与圆有哪些位置关系? ..........点与圆的位置关系有三种:
点在圆内,
点在圆上,
点在圆外思考:点与圆的位置与这些点与圆心的距离有何关系 我们知道圆上所有的点到圆心的距离都等于半径,如图,设⊙O的半径为r,A点在圆内,B点在圆上,C点在圆外,那么有:
OA___r,
OB___r,
OC___r=><O圆上的点到圆心的距离等于半径,圆外的点到圆心的距离大于半径,圆内的点到圆心的距离小于半径.
反之也成立. 到圆心的距离等于半径的点在圆上,大于半径的点在圆外,小于半径的点在圆内.设⊙O的半径为r,点到圆心的距离为d。则点和圆的位置关系点在圆内d﹤r点在圆上点在圆外d=rd>rO1.已知圆的半径等于5厘米,点到圆心的距离是:
①8厘米 ②4厘米 ③5厘米。
请你分别说出点与圆的位置关系。例题与练习
2、已知⊙O的半径为4,OP=3.4,则P在⊙O的 ( )。
3、已知 点P在 ⊙O的外部,OP=5,那么⊙O的半径r满足( )
4,已知⊙O的半径为5,M为ON的中点,当OM=3时,N点与⊙O的位置关系是N在⊙O的( )内部0﹤r ﹤5外部1.已知圆的半径等于5cm,根据下列点P到圆心的距离:(1)4cm;(2)5cm;(3)6cm;判定点P与圆的位置关系,并说明理由.
2.点A在以O为圆心,3cm为半径的⊙O内,则点A到圆心O的距离d的范围是
3.P为⊙O内与O不重合的一点,则下列说法正确的是( )
A.点P到⊙O上任一点的距离都小于⊙O的半径
B.⊙O上有两点到点P的距离等于⊙O的半径
C.⊙O上有两点到点P的距离最小
D.⊙O上有两点到点P的距离最大4.若⊙A的半径为5,点A的坐标为(3,4),点P的坐标为(5,8),则点P的位置为( )
A.在⊙A内 B.在⊙A上 C.在⊙A外 D.不确定
5.两个圆心为O的甲,乙两圆,半径分别为r1和r2,且r1<OA<r2,那么点A在( )
A.甲圆内 B.乙圆外 C.甲圆外,乙圆内 D.甲圆内,乙圆外
7.⊙O的半径为5,圆心O的坐标为(0,0),点P的坐标为(4,2),则点P与⊙O的位置关系( )
A.点P在⊙O内 B.点P在⊙O上
C.点P在⊙O外 D.点P在⊙O上或⊙O外
8.在△ABC中,∠C=90°,AC=BC=4cm,D是AB边的中点,以C为圆心,4cm长为半径作圆,则A.B,C,D四点中在圆内的有( )
A.1个 B.2个 C.3个 D.4个
9,一点和⊙O上的最近点距离为4cm,最远距离为9cm,则这圆的半径是 cm.5.Rt△ABC中,∠C=90°,CD⊥AB,AB=10,AC=6,以C点为圆心,6为半径画圆,则点A,B,D与圆的位置关系是怎样的?84.8....1,在Rt△ABC中,∠C=90°,AB=15cm,BC=10cm,以A为圆心,12cm为半径作圆,则点C与⊙A的位置关系是 .
2.⊙O的半径是3cm,P是⊙O内一点,PO=1cm,则点P到⊙O上各点的最小距离是 .
3.作图说明:到已知点A的距离大于或等于1cm,且小于或等于2cm的所有点组成的图形.
独立思考经过三点的圆A.过一点可以
画无数个圆.过一点作圆探究(1)
1、过一个已知点A如何作圆? 2、过点A所作圆的圆心在哪里?半径多大?可以作几个这样的圆?..AB过A,B两点有无数个圆,
圆心都在线段AB的中垂线上......过两点作圆探究(2)
1、过已知两点A、B如何作圆? 2、圆心A、B两点的距离怎样?能用式子表示吗?圆心在哪里?过点A、B两点的圆有几个? ...ABC.O1.不在同一条直线上的三个点确定一个圆分两种情形2.如果A,B,C三点在一条直线上,经过这三点你能画圆吗?ACB...经过三点作圆...ABC.O经过三角形三个顶点可以画一个圆,并且只能画一个.经过三角形三个顶点的圆叫做三角形的外接圆.三角形外接圆的圆心叫做这个三角形的外心;外心就是三角形三条边的垂直平分线的交点.这个三角形叫做这个圆的内接三角形.△ABC⊙O判断正误
1.经过三个点一定可以作圆.
2.任意一个三角形一定有一个外接圆.
3.任意一个圆一定有一内接三角形,并且只有一个内接三角形.
4.三角形的外心到三角形各个顶点的距离都相等.三角形的外心是否一定在三角形的内部?直角三角形外心是斜边AB的中点钝角三角形外心在△ABC的外面任意画一个直角三角形,然后再画这个三角形的
外接圆.如果是一个钝角三角形呢?
1.过点作圆
(1)过一点作圆
(2)过两点作圆
(3)过三点作圆
2.三角形的外接圆
今天我们学到了……练习判断题:(1)任意一个三角形一定有一个外接圆,
并且只有一个外接圆;(?? ) (2)任意一个圆一定有一个内接三角形,
并且只有一个内接三角形;(?? ) 随堂练习(3)三角形的外心到三角形各顶点的距
离相等.(?? )(4)三角形的外心在三角形的外部,
此三角形就是锐角三角形。( ) (5)过同一平面上的四点一定能做一个
圆。( ) 随堂练习随堂练习
1. 如果直角三角形的两条直角边分别是6,8,你能求出这个直角三角形的外接圆的半径吗?是多少?
2.在△ABC中,AB=AC=13,BC=10,试求这个三角形的外接圆的面积.应用 某一个城市在一块空地新建了三个居民小区,它们分别为A、B、C,且三个小区不在同一直线上,要想规划一所中学,使这所中学到三个小区的距离相等。请问同学们这所中学建在哪个位置?你怎么确定这个位置呢?●●●BAC三、思考题:
1.经过四个点是不是一定能作圆?所以经过四点不一定能作圆。4、2.思考题
①过三角形的三个顶点是否都可以作圆?为什么?
②一个三角形的外接圆有几个?一个圆的内接三角形有几个?为什么?
③三角形的外心有什么性质?它一定在三角形的内部吗?画图说明。3.想一想:
图中工具的CD边所在的直线恰好垂直平分
AB边,怎样用这个工具找出一个圆的圆心?
同课章节目录
