高中数学必修第一册人教A版(2019)第四章《指数函数与对数函数》章末复习学案(含答案)
文档属性
| 名称 | 高中数学必修第一册人教A版(2019)第四章《指数函数与对数函数》章末复习学案(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 641.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-08 00:00:00 | ||
图片预览



文档简介
《指数函数与对数函数》章末复习
专题1 指数函数、对数函数的定义域、值域及有关计算
从近几年高考试题分析来看,求函数的定义域是高考的热点问题,多与对数函数结合命题,题型以选择题、填空题为主,难度较小,属容易题.
函数的求值问题在近几年的高考中经常出现,是考查的重点之一,主要考查一次函数、二次函数、指数函数及对数函数的求值.
例1(1)(江西高考)函数的定义域为( ).
A.(0,1)
B.[0,1)
C.(0,1]
D.[0,1]
(2)(广东高考)函数的定义域是( ).
A.(-1,+∞)
B.[-1,+∞)
C.(-1,1)∪(1,+∞)
D.[-1,1)∪(1,+∞)
(3)(2018·全国I高考)已知函数,若,则a= .
(4)(浙江高考)已知函数,则 ,的最小值是 .
(5)(山东高考)已知函数的定义域和值域都是[-1,0],则
a+b= .
解(1)由,解得0≤x<1,故选B.
(2)由x+1>0且x-1.故选C.
(3).
(4)1+2-3=0.当x≥1时,当x<1时,,.
综上,.
(5)当01时,解得,无解.综上,.
答(1)B(2)C(3)-7(4)0 (5)
专题2 指数函数、对数函数的单调性与奇偶性的研究
从近几年的高考试题来看,指数函数、对数函数的性质是高考的热点,题型一般为选择题、填空题,属中档题,主要考查函数的奇偶性、单调性.
例2(1)(2017·全国I高考)已知函数,则( ).
A.在(0,2)上单调递增
B.在(0,2)上单调递减
C.的图像关于直线x=1对称
D.的图像关于点(1,0)对称
(2)已知a>0,且a≠1,函数在上单调递减,则( ).
A.在(-∞,-1)上单调递减,在(-1,1)上单调递增
B.在(-∞,-1)上单调递增,在(-1,1)上单调递减
C.在(-∞,-1)上单调递增,在(-1,1)上单调递增
D.在(-∞,-1)上单调递减,在(-1,1)上单调递减
解(1)由题知(0(2)令当x>1时,,t在(1,+∞)上单调递增,而在(1,+∞)上单调递减,所以单调递减,即0答(1)C(2)A
专题3 指数函数、对数函数的图像及其应用
(1)图像的画法与变换
重点考查识图、用图、画图等方面的能力,多以选择题、填空题的形式出现.函数的图像是数形结合的典范,纵观近几年高考试题,函数图像的考查涉及的知识面广、形式灵活,经常会以新面孔出现,是每年的必考内容.
例3(1)(2018·哈尔滨三中高一期中考试)已知函数=,则的图像大致是( ).
A.
B.
C.
D.
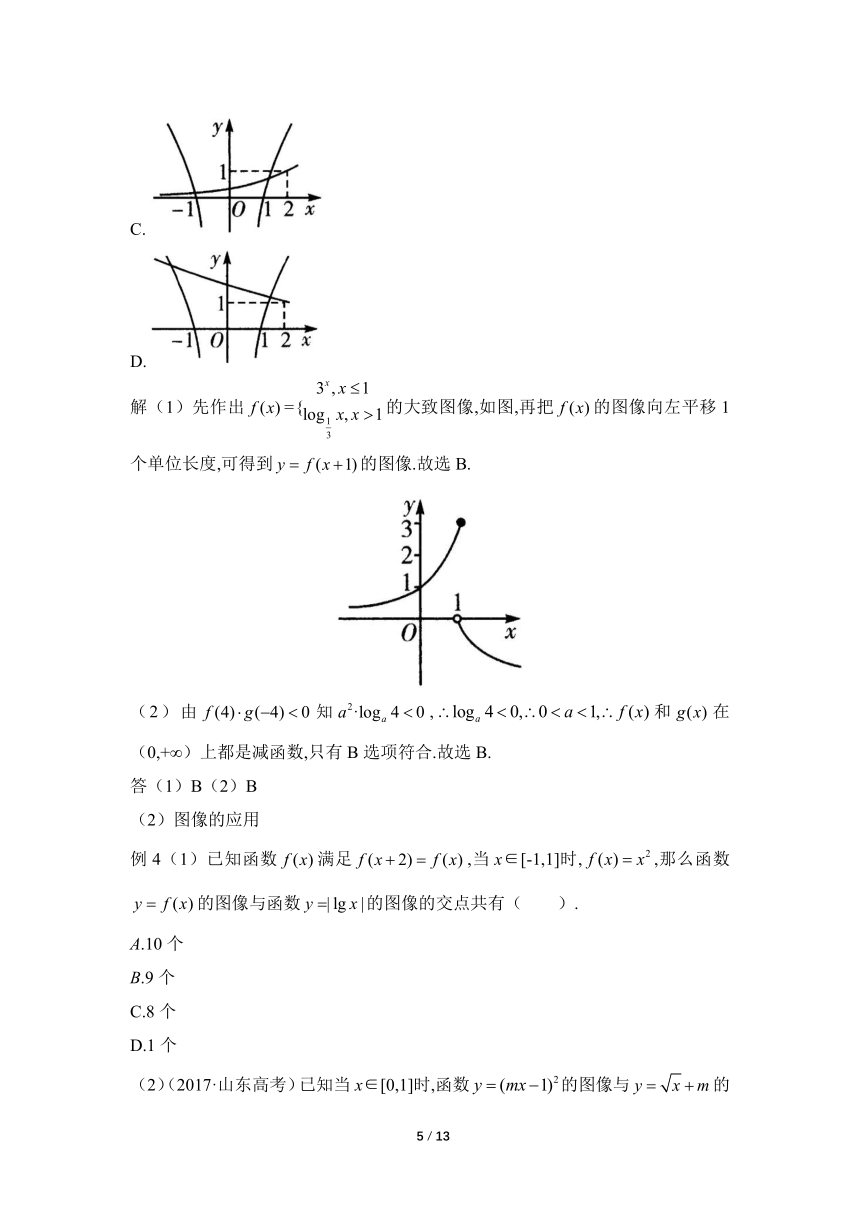
(2)(2019·广东清远高三八月调考)已知,,若,则在同一平面直角坐标系内的大致图像是( ).
A.
B.
C.
D.
解(1)先作出=的大致图像,如图,再把的图像向左平移1个单位长度,可得到的图像.故选B.
(2)由知,和在(0,+∞)上都是减函数,只有B选项符合.故选B.
答(1)B(2)B
(2)图像的应用
例4(1)已知函数满足,当x∈[-1,1]时,,那么函数的图像与函数的图像的交点共有( ).
A.10个
B.9个
C.8个
D.1个
(2)(2017·山东高考)已知当x∈[0,1]时,函数的图像与的图像有且只有一个交点,则正实数m的取值范围是( ).
A.(0,1]∪[,+∞)
B.(0,1]∪[3,+∞)
C.(0,]∪[,+∞)
D.(0,]∪[3,+∞)
解(1)画出这两个函数的图像,如图所示,可以看出交点有10个.故选A.
(2)当x∈[0,1]时,的值域为[m,m+1],且在[0,1]上单调递增..由m>0,①当≥1,即0②当<1,即m>1时,函数在上单调递减,在
上单调递增,值域为.如图,若两函数图像在[0,1]上有且只有一个交点,则,解得m≥3.综上所述,m的取值范围是(0,1] [3,+∞).故选B.
答(1)A(2)B
专题4 比较大小与求参数的范围
(1)幂值的大小比较
比较两个数(式)或几个数(式)的大小问题是一个重要题型,它主要是考查幂函数、指数函数、对数函数图像与性质的应用及差值比较法与商值比较法的应用,常用的方法有单调性法、图像中间量搭桥法、作差法、作商法等
例5(1)(山东高考)设,则a,b,c的大小关系是( ).
A.aB.aC.bD.b(2)(2018·云南曲靖一中高一月考)若0A.
B.
C.
D.
解(1)因为函数是减函数,0<0.6<1.5,所以1>,即b1.综上,b
(2)因为0答(1)C(2)C
(2)求参数的范围
例6(1)(全国‖高考)设函数,则使得成立的x的取值范围是( ).
A.
B.
C.
D.
(2)(湖南高考)已知函数与的图像上存在关于y轴对称的点,则a的取值范围是( ).
A.
B.
C.
D.
(3)(2019·广西玉林高三八月摸底考试)当0A.
B.
C.
D.
解(1)由可知是偶函数,且在[0,+∞)上是增函数,所以.故选A.
(2)由题可得存在∈(-∞,0)满足
,令.因为函数在定义域内都是单调递增的,所以函数在定义域内是单调递增的.又因为当x趋近于-∞时,函数h(x)<0,且h(x)=0在(-∞,0)上有解(即函数h(x)有零点),所以h(0)=,故选B.
(3)易知0答(1)A(2)B(3)B
专题5 函数的零点(方程的根)的讨论
(1)求零点的个数
求函数零点有两种基本方法:一是求方程f(x)=0的实根;二是当方程的实根不易求解时,将它与函数y=f(x)的图像联系起来,综合函数零点的性质与函数图像的性质找出零点.
例5(1)(天津高考)函数在区间(0,1)内的零点个数是( ).
A.0
B.1
C.2
D.3
(2)(江苏高考)已知函数,g(x)=,则方程的实根的个数为 .
解(1)解法一:因为f(0)=1+0-2=-1,f(1)=2+1-2=1,即f(0)·f(1)<0且函数f(x)在(0,1)内单调递增且连续不断,故f(x)在(0,1)内的零点个数是1.
解法二:设,在同一坐标系中作出两函数的图像如图所示,可知B正确.
(2)由可得f(x)+g(x)=±1,即g(x)=f(x)±1,则原问题等价于函数y=g(x)与y=-f(x)+1或y=g(x)与y=-f(x)-1的图像的交点个数问题,在同一坐标系中作出y=g(x),y=-f(x)+1及y=-f(x)-1的图像,如图.
由图可知,函数y=g(x)的图像与函数y=-f(x)+1的图像有2个交点,与函数y=-f(x)-1的图像有2个交点,则方程实根的个数为4.
答(1)B(2)4
(2)利用函数零点的个数求参数范围
例8(2019·天津高考)已知函数若关于x的方程
恰有两个互异的实数解,则a的取值范围为( ).
A.
B.
C.
D.
解如图,当直线位于B点及其上方且位于A点及其下方,或者直线与曲线相切在第一象限时符合要求,即,即或者,得,即,得a=1,所以a的取值范围是.故选D.
答D
专题6 函数模型的实际应用
通过对近几年高考试题的分析可以看出,对函数的实际应用问题的考查,更多地以社会实际生活为背景,设问新颖、灵活,题型以解答题为主,难度中等偏上,主要考查建模能力,同时考查分析问题解决问题的能力.
例9 某食品的保鲜时间y(单位:h)与储存温度x(单位:℃)满足函数关系为自然对数的底数,k,b为常数),该食品在0℃的保鲜时间是192h,在16℃的保鲜时间是12h,若要使该食品的保鲜时间至少是96h,则储存温度x最大不能高于 ℃.
解为自然对数的底数,k,b为常数).
当x=0时,,
当x=16时,
即.
若,则,
即,即.,则x=4,即储存温度x最大不能高于4℃,故答案为4.
答4
例10(2019河南许昌高中高一期中检测)载人飞船是通过火箭发射的.已知某型号火箭的起飞重量Mt是箭体(包括搭载的飞行器)的重量mt和燃料重量xt之和.在不考虑空气阻力的条件下,假设火箭的最大速度ykm/s关于x的函数关系为.当燃料重量为mt时,该火箭的最大速度为4km/s.
(1)求此型号火箭的最大速度ykm/s与燃料重量xt之间的函数关系式;
(2)若此型号火箭的起飞重量是479.8t,则应装载多少吨燃料(精确到0.1t,取e≈2.718)才能使火箭的最大飞行速度达到8km/s,顺利地把飞船发送到预定的椭圆轨道?
解(1)由题意,得,解得k=8,
所以.
(2)由已知,得M=m+x=479.8,则m=479.8-x.
将y=8代入(1)中所得式中,得,解得x≈303.3
所以应装载大约303.3t燃料,才能使火箭的最大飞行速度达到8km/s,顺利地把飞船发送到预定的椭圆轨道.
1 / 13
专题1 指数函数、对数函数的定义域、值域及有关计算
从近几年高考试题分析来看,求函数的定义域是高考的热点问题,多与对数函数结合命题,题型以选择题、填空题为主,难度较小,属容易题.
函数的求值问题在近几年的高考中经常出现,是考查的重点之一,主要考查一次函数、二次函数、指数函数及对数函数的求值.
例1(1)(江西高考)函数的定义域为( ).
A.(0,1)
B.[0,1)
C.(0,1]
D.[0,1]
(2)(广东高考)函数的定义域是( ).
A.(-1,+∞)
B.[-1,+∞)
C.(-1,1)∪(1,+∞)
D.[-1,1)∪(1,+∞)
(3)(2018·全国I高考)已知函数,若,则a= .
(4)(浙江高考)已知函数,则 ,的最小值是 .
(5)(山东高考)已知函数的定义域和值域都是[-1,0],则
a+b= .
解(1)由,解得0≤x<1,故选B.
(2)由x+1>0且x-1.故选C.
(3).
(4)1+2-3=0.当x≥1时,当x<1时,,.
综上,.
(5)当0
答(1)B(2)C(3)-7(4)0 (5)
专题2 指数函数、对数函数的单调性与奇偶性的研究
从近几年的高考试题来看,指数函数、对数函数的性质是高考的热点,题型一般为选择题、填空题,属中档题,主要考查函数的奇偶性、单调性.
例2(1)(2017·全国I高考)已知函数,则( ).
A.在(0,2)上单调递增
B.在(0,2)上单调递减
C.的图像关于直线x=1对称
D.的图像关于点(1,0)对称
(2)已知a>0,且a≠1,函数在上单调递减,则( ).
A.在(-∞,-1)上单调递减,在(-1,1)上单调递增
B.在(-∞,-1)上单调递增,在(-1,1)上单调递减
C.在(-∞,-1)上单调递增,在(-1,1)上单调递增
D.在(-∞,-1)上单调递减,在(-1,1)上单调递减
解(1)由题知(0
专题3 指数函数、对数函数的图像及其应用
(1)图像的画法与变换
重点考查识图、用图、画图等方面的能力,多以选择题、填空题的形式出现.函数的图像是数形结合的典范,纵观近几年高考试题,函数图像的考查涉及的知识面广、形式灵活,经常会以新面孔出现,是每年的必考内容.
例3(1)(2018·哈尔滨三中高一期中考试)已知函数=,则的图像大致是( ).
A.
B.
C.
D.
(2)(2019·广东清远高三八月调考)已知,,若,则在同一平面直角坐标系内的大致图像是( ).
A.
B.
C.
D.
解(1)先作出=的大致图像,如图,再把的图像向左平移1个单位长度,可得到的图像.故选B.
(2)由知,和在(0,+∞)上都是减函数,只有B选项符合.故选B.
答(1)B(2)B
(2)图像的应用
例4(1)已知函数满足,当x∈[-1,1]时,,那么函数的图像与函数的图像的交点共有( ).
A.10个
B.9个
C.8个
D.1个
(2)(2017·山东高考)已知当x∈[0,1]时,函数的图像与的图像有且只有一个交点,则正实数m的取值范围是( ).
A.(0,1]∪[,+∞)
B.(0,1]∪[3,+∞)
C.(0,]∪[,+∞)
D.(0,]∪[3,+∞)
解(1)画出这两个函数的图像,如图所示,可以看出交点有10个.故选A.
(2)当x∈[0,1]时,的值域为[m,m+1],且在[0,1]上单调递增..由m>0,①当≥1,即0
上单调递增,值域为.如图,若两函数图像在[0,1]上有且只有一个交点,则,解得m≥3.综上所述,m的取值范围是(0,1] [3,+∞).故选B.
答(1)A(2)B
专题4 比较大小与求参数的范围
(1)幂值的大小比较
比较两个数(式)或几个数(式)的大小问题是一个重要题型,它主要是考查幂函数、指数函数、对数函数图像与性质的应用及差值比较法与商值比较法的应用,常用的方法有单调性法、图像中间量搭桥法、作差法、作商法等
例5(1)(山东高考)设,则a,b,c的大小关系是( ).
A.a
B.
C.
D.
解(1)因为函数是减函数,0<0.6<1.5,所以1>,即b
(2)求参数的范围
例6(1)(全国‖高考)设函数,则使得成立的x的取值范围是( ).
A.
B.
C.
D.
(2)(湖南高考)已知函数与的图像上存在关于y轴对称的点,则a的取值范围是( ).
A.
B.
C.
D.
(3)(2019·广西玉林高三八月摸底考试)当0
B.
C.
D.
解(1)由可知是偶函数,且在[0,+∞)上是增函数,所以.故选A.
(2)由题可得存在∈(-∞,0)满足
,令.因为函数在定义域内都是单调递增的,所以函数在定义域内是单调递增的.又因为当x趋近于-∞时,函数h(x)<0,且h(x)=0在(-∞,0)上有解(即函数h(x)有零点),所以h(0)=,故选B.
(3)易知0
专题5 函数的零点(方程的根)的讨论
(1)求零点的个数
求函数零点有两种基本方法:一是求方程f(x)=0的实根;二是当方程的实根不易求解时,将它与函数y=f(x)的图像联系起来,综合函数零点的性质与函数图像的性质找出零点.
例5(1)(天津高考)函数在区间(0,1)内的零点个数是( ).
A.0
B.1
C.2
D.3
(2)(江苏高考)已知函数,g(x)=,则方程的实根的个数为 .
解(1)解法一:因为f(0)=1+0-2=-1,f(1)=2+1-2=1,即f(0)·f(1)<0且函数f(x)在(0,1)内单调递增且连续不断,故f(x)在(0,1)内的零点个数是1.
解法二:设,在同一坐标系中作出两函数的图像如图所示,可知B正确.
(2)由可得f(x)+g(x)=±1,即g(x)=f(x)±1,则原问题等价于函数y=g(x)与y=-f(x)+1或y=g(x)与y=-f(x)-1的图像的交点个数问题,在同一坐标系中作出y=g(x),y=-f(x)+1及y=-f(x)-1的图像,如图.
由图可知,函数y=g(x)的图像与函数y=-f(x)+1的图像有2个交点,与函数y=-f(x)-1的图像有2个交点,则方程实根的个数为4.
答(1)B(2)4
(2)利用函数零点的个数求参数范围
例8(2019·天津高考)已知函数若关于x的方程
恰有两个互异的实数解,则a的取值范围为( ).
A.
B.
C.
D.
解如图,当直线位于B点及其上方且位于A点及其下方,或者直线与曲线相切在第一象限时符合要求,即,即或者,得,即,得a=1,所以a的取值范围是.故选D.
答D
专题6 函数模型的实际应用
通过对近几年高考试题的分析可以看出,对函数的实际应用问题的考查,更多地以社会实际生活为背景,设问新颖、灵活,题型以解答题为主,难度中等偏上,主要考查建模能力,同时考查分析问题解决问题的能力.
例9 某食品的保鲜时间y(单位:h)与储存温度x(单位:℃)满足函数关系为自然对数的底数,k,b为常数),该食品在0℃的保鲜时间是192h,在16℃的保鲜时间是12h,若要使该食品的保鲜时间至少是96h,则储存温度x最大不能高于 ℃.
解为自然对数的底数,k,b为常数).
当x=0时,,
当x=16时,
即.
若,则,
即,即.,则x=4,即储存温度x最大不能高于4℃,故答案为4.
答4
例10(2019河南许昌高中高一期中检测)载人飞船是通过火箭发射的.已知某型号火箭的起飞重量Mt是箭体(包括搭载的飞行器)的重量mt和燃料重量xt之和.在不考虑空气阻力的条件下,假设火箭的最大速度ykm/s关于x的函数关系为.当燃料重量为mt时,该火箭的最大速度为4km/s.
(1)求此型号火箭的最大速度ykm/s与燃料重量xt之间的函数关系式;
(2)若此型号火箭的起飞重量是479.8t,则应装载多少吨燃料(精确到0.1t,取e≈2.718)才能使火箭的最大飞行速度达到8km/s,顺利地把飞船发送到预定的椭圆轨道?
解(1)由题意,得,解得k=8,
所以.
(2)由已知,得M=m+x=479.8,则m=479.8-x.
将y=8代入(1)中所得式中,得,解得x≈303.3
所以应装载大约303.3t燃料,才能使火箭的最大飞行速度达到8km/s,顺利地把飞船发送到预定的椭圆轨道.
1 / 13
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
