【新课标】5.1.1 一元一次方程 课件(共30张PPT)
文档属性
| 名称 | 【新课标】5.1.1 一元一次方程 课件(共30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-08 15:47:23 | ||
图片预览











文档简介
(共30张PPT)
5.1.1 一元一次方程
北师版七年级上册
教学目标
1.通过分析具体问题中的数量关系列出一元一次方程,感受方程作为刻画现实世界的有效模型.
2.通过观察,归纳一元一次方程的概念.
教学重难点
重点:
掌握一元一次方程的定义。
难点:
能根据具体问题的数量关系列出方程。
新知导入
丢番图是古希腊数学家。
人们对他的生平事迹知道得很少,但流传着一篇墓志铭叙述了他的生平:坟中安葬着丢番图, 多么令人惊讶,它忠实地记录了其所经历的人生旅程。上帝赐予他的童年占六分之一, 又过十二分之一他两颊长出了胡须, 再过七分之一,点燃了新婚的蜡烛。五年之后喜得贵子, 可怜迟到的宁馨儿, 享年仅及其父之半便入黄泉。悲伤只有用数学研究去弥补, 又过四年,他也走完了人生的旅途.
你能用方程求出丢番图去世时的年龄吗?
新知讲解
小华 小彬
我 能 猜
出你的年龄
你的年龄
乘 2 减 5 得数是多少?
小华 小彬
21
新知讲解
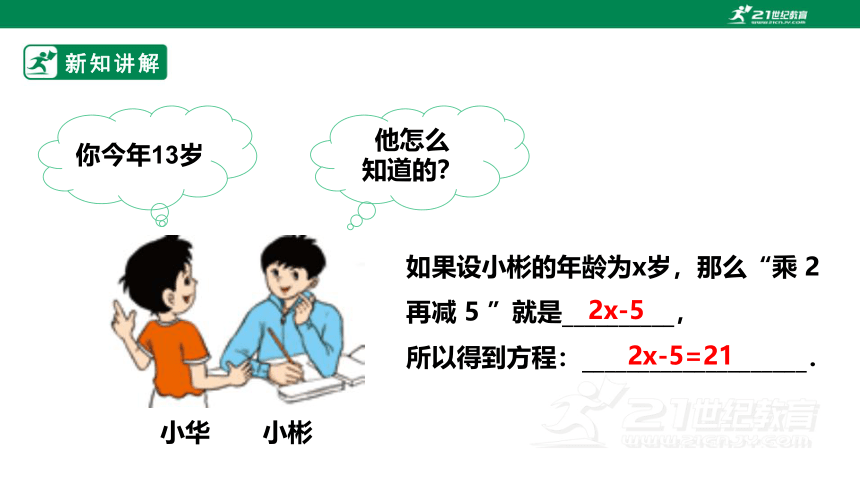
你今年13岁
小华 小彬
他怎么
知道的?
如果设小彬的年龄为x岁,那么“乘 2 再减 5 ”就是__________,
所以得到方程:____________________.
2x-5
2x-5=21
新知讲解
2.小颖种了一株树苗,开始时树苗高为 40 cm,栽种后每周树苗长高约 5 cm,大约几周后树苗长高到 1 m?
如果设 x 周后树苗长高到 1 m,那么可以得到方程:
_________________________。
40+5x=100
3.甲、乙两地相距 22 km,张叔叔从甲地出发到乙地,每时比原计划多行走1 km,因此提前 12 min 到达乙地,张叔叔原计划每时行走多少千米?
设张叔叔原计划每时行走 x km,可以得到方程:_________________ .
新知讲解
4.根据第六次全国人口普查统计数据,截至 2010 年 11 月 1 日 0 时,全国每 10 万人中具有大学文化程度的人数为 8 930 人,与 2000 年第五次全国人口普查相比增长了 147.30%.
如果设 2000 年第五次全国人口普查时每 10 万人中约有 x 人具
有大学文化程度,那么可以得到方程:__________________________.
(1+147.30%)x=8930
新知讲解
5.某长方形操场的面积是 5 850 m2,长和宽之差为 25 m,这个操场的长与宽分别是多少米?
如果设这个操场的宽为 x m,那么长为(x + 25)m.由此可以得到方程:____________________________.
x(x + 25)=5850
新知讲解
上面的几个题目中得出了几个方程。
2x-5=21
40+5x=100
(1+147.30%)x=8930
x(x + 25)=5850
什么是方程?
方程有什么特点?
新知讲解
上面的几个题目中得出了几个方程。
2x-5=21
40+5x=100
(1+147.30%)x=8930
x(x + 25)=5850
含有未知数的等式叫做方程.
方程的特点:
①方程中一定含有未知数;
②方程是等式.
新知讲解
【思考】判断下列式子是不是方程?
(1)x+2=3 (2)x+3y=6
(3)3x-6 (4)1+2=3
(5)x+3>5 (6)y-12=5
是
是
是
不是
不是
不是
新知讲解
【总结归纳】
(1)方程中包含两个要求:
①必须是等式;②必须含有未知数;两者缺一不可.
(2)方程一定是等式,但等式不一定是方程;
(3)方程中的未知数可以用x表示,也可以用其他字母表示;
(4)方程中可含多个未知数.
新知讲解
观察下面的方程,你能发现什么特点?
2x-5=21
40+5x=100
(1+147.30%)x=8930
x(x + 25)=5850
只含有一个未知数.
未知数的指数都是1.
等号的两边都是整式
新知讲解
在一个方程中,只含有一个未知数,且未知数的指数都是 1,这样的方程叫做一元一次方程。
一元一次方程
使方程左、右两边的值相等的未知数的值,叫做方程的解.
新知讲解
【例】下列方程中是一元一次方程的是( )
A.x2-4x+3=0
B.3x-4y=7
C.3x+2=0
D. =9
C
新知讲解
【总结归纳】
(1)一元一次方程的标准形式:ax+b=0(a≠0),其中x是未知数,a,b是已知数;
(2)一元一次方程的条件:
①方程中的代数式都是整式;
②是方程;
③只含一个未知数且化简后未知数的系数不为0;
④未知数的指数都是1(化简后).
新知讲解
想一想:怎样根据实际问题列出方程呢?
①设未知数(通常用x,y,z等字母表示),分直接设和间接设两种,一般求什么就设什么;
②分析已知量与未知量之间的关系,找出相等关系(或等量关系);
③列方程,即用含有未知数的代数式表示相等关系中左、右两边的量;
④解答。
新知讲解
【例】育才中学七年级共有328名师生,十一黄金周组织秋游,需要租车,已知有2辆校车可乘坐64人,还需要租用44个座位的客车多少辆
解:设还需要租用44个座位的客车x辆,则客车可坐44x人.
根据题意列方程,得44x+64=328.
本题的相等关系是:
乘坐校车的人数+乘坐客车的人数=师生总人数.
课堂练习
1.下列各式中,是方程的是( )
A.-1+1=0
B.x-2=0
C.2x-1
D.x-1≠0
B
课堂练习
2.下列各式中,是一元一次方程的有( )
①x2-4x=-3; ②3x-1=2x ; ③x+2y=1;
④xy-3=5; ⑤5x-x=3.
A.1个
B.2个
C.3个
D.4个
B
课堂练习
3.若关于x的方程(m-3)x+6=0是一元一次方程,则m的取值范围是( )
A.m≠0
B.m≠2
C.m=2
D.m≠3
D
课堂练习
4.如图,在编写数学谜题时,“□”内要求填写同一个数字,若设“□”内数字为x,则列出方程正确的是( )
A.3×2x+5=2x
B.3×20x+5=10x×2
C.3×20+x+5=20x
D.3×(20+x)+5=10x+2
D
课堂练习
5.若(m-2)x|2m-3|=6是关于x的一元一次方程,求m的值。
解:由题意得:|2m-3|=1,所以m=1或m=2.
又因为x的系数不为0,即m-2≠0,故m≠2.
所以m=1.
课堂练习
6.方程2x+3=7的解是( ).
A.x=5
B.x=4
C.x=3.5
D.x=2
D
课堂总结
本节课你学到了什么?
1.含有未知数的等式叫做方程.
2.在一个方程中,只含有一个未知数,且未知数的指数都是 1,这样的方程叫做一元一次方程.
3.使方程左、右两边的值相等的未知数的值,叫做方程的解.
板书设计
课题:5.1.1 一元一次方程
教师板演区
学生展示区
一、方程的定义.
二、一元一次方程的定义
三、方程的解.
四、列一元一次方程
作业布置
课本 P132 习题5.1
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
5.1.1 一元一次方程
北师版七年级上册
教学目标
1.通过分析具体问题中的数量关系列出一元一次方程,感受方程作为刻画现实世界的有效模型.
2.通过观察,归纳一元一次方程的概念.
教学重难点
重点:
掌握一元一次方程的定义。
难点:
能根据具体问题的数量关系列出方程。
新知导入
丢番图是古希腊数学家。
人们对他的生平事迹知道得很少,但流传着一篇墓志铭叙述了他的生平:坟中安葬着丢番图, 多么令人惊讶,它忠实地记录了其所经历的人生旅程。上帝赐予他的童年占六分之一, 又过十二分之一他两颊长出了胡须, 再过七分之一,点燃了新婚的蜡烛。五年之后喜得贵子, 可怜迟到的宁馨儿, 享年仅及其父之半便入黄泉。悲伤只有用数学研究去弥补, 又过四年,他也走完了人生的旅途.
你能用方程求出丢番图去世时的年龄吗?
新知讲解
小华 小彬
我 能 猜
出你的年龄
你的年龄
乘 2 减 5 得数是多少?
小华 小彬
21
新知讲解
你今年13岁
小华 小彬
他怎么
知道的?
如果设小彬的年龄为x岁,那么“乘 2 再减 5 ”就是__________,
所以得到方程:____________________.
2x-5
2x-5=21
新知讲解
2.小颖种了一株树苗,开始时树苗高为 40 cm,栽种后每周树苗长高约 5 cm,大约几周后树苗长高到 1 m?
如果设 x 周后树苗长高到 1 m,那么可以得到方程:
_________________________。
40+5x=100
3.甲、乙两地相距 22 km,张叔叔从甲地出发到乙地,每时比原计划多行走1 km,因此提前 12 min 到达乙地,张叔叔原计划每时行走多少千米?
设张叔叔原计划每时行走 x km,可以得到方程:_________________ .
新知讲解
4.根据第六次全国人口普查统计数据,截至 2010 年 11 月 1 日 0 时,全国每 10 万人中具有大学文化程度的人数为 8 930 人,与 2000 年第五次全国人口普查相比增长了 147.30%.
如果设 2000 年第五次全国人口普查时每 10 万人中约有 x 人具
有大学文化程度,那么可以得到方程:__________________________.
(1+147.30%)x=8930
新知讲解
5.某长方形操场的面积是 5 850 m2,长和宽之差为 25 m,这个操场的长与宽分别是多少米?
如果设这个操场的宽为 x m,那么长为(x + 25)m.由此可以得到方程:____________________________.
x(x + 25)=5850
新知讲解
上面的几个题目中得出了几个方程。
2x-5=21
40+5x=100
(1+147.30%)x=8930
x(x + 25)=5850
什么是方程?
方程有什么特点?
新知讲解
上面的几个题目中得出了几个方程。
2x-5=21
40+5x=100
(1+147.30%)x=8930
x(x + 25)=5850
含有未知数的等式叫做方程.
方程的特点:
①方程中一定含有未知数;
②方程是等式.
新知讲解
【思考】判断下列式子是不是方程?
(1)x+2=3 (2)x+3y=6
(3)3x-6 (4)1+2=3
(5)x+3>5 (6)y-12=5
是
是
是
不是
不是
不是
新知讲解
【总结归纳】
(1)方程中包含两个要求:
①必须是等式;②必须含有未知数;两者缺一不可.
(2)方程一定是等式,但等式不一定是方程;
(3)方程中的未知数可以用x表示,也可以用其他字母表示;
(4)方程中可含多个未知数.
新知讲解
观察下面的方程,你能发现什么特点?
2x-5=21
40+5x=100
(1+147.30%)x=8930
x(x + 25)=5850
只含有一个未知数.
未知数的指数都是1.
等号的两边都是整式
新知讲解
在一个方程中,只含有一个未知数,且未知数的指数都是 1,这样的方程叫做一元一次方程。
一元一次方程
使方程左、右两边的值相等的未知数的值,叫做方程的解.
新知讲解
【例】下列方程中是一元一次方程的是( )
A.x2-4x+3=0
B.3x-4y=7
C.3x+2=0
D. =9
C
新知讲解
【总结归纳】
(1)一元一次方程的标准形式:ax+b=0(a≠0),其中x是未知数,a,b是已知数;
(2)一元一次方程的条件:
①方程中的代数式都是整式;
②是方程;
③只含一个未知数且化简后未知数的系数不为0;
④未知数的指数都是1(化简后).
新知讲解
想一想:怎样根据实际问题列出方程呢?
①设未知数(通常用x,y,z等字母表示),分直接设和间接设两种,一般求什么就设什么;
②分析已知量与未知量之间的关系,找出相等关系(或等量关系);
③列方程,即用含有未知数的代数式表示相等关系中左、右两边的量;
④解答。
新知讲解
【例】育才中学七年级共有328名师生,十一黄金周组织秋游,需要租车,已知有2辆校车可乘坐64人,还需要租用44个座位的客车多少辆
解:设还需要租用44个座位的客车x辆,则客车可坐44x人.
根据题意列方程,得44x+64=328.
本题的相等关系是:
乘坐校车的人数+乘坐客车的人数=师生总人数.
课堂练习
1.下列各式中,是方程的是( )
A.-1+1=0
B.x-2=0
C.2x-1
D.x-1≠0
B
课堂练习
2.下列各式中,是一元一次方程的有( )
①x2-4x=-3; ②3x-1=2x ; ③x+2y=1;
④xy-3=5; ⑤5x-x=3.
A.1个
B.2个
C.3个
D.4个
B
课堂练习
3.若关于x的方程(m-3)x+6=0是一元一次方程,则m的取值范围是( )
A.m≠0
B.m≠2
C.m=2
D.m≠3
D
课堂练习
4.如图,在编写数学谜题时,“□”内要求填写同一个数字,若设“□”内数字为x,则列出方程正确的是( )
A.3×2x+5=2x
B.3×20x+5=10x×2
C.3×20+x+5=20x
D.3×(20+x)+5=10x+2
D
课堂练习
5.若(m-2)x|2m-3|=6是关于x的一元一次方程,求m的值。
解:由题意得:|2m-3|=1,所以m=1或m=2.
又因为x的系数不为0,即m-2≠0,故m≠2.
所以m=1.
课堂练习
6.方程2x+3=7的解是( ).
A.x=5
B.x=4
C.x=3.5
D.x=2
D
课堂总结
本节课你学到了什么?
1.含有未知数的等式叫做方程.
2.在一个方程中,只含有一个未知数,且未知数的指数都是 1,这样的方程叫做一元一次方程.
3.使方程左、右两边的值相等的未知数的值,叫做方程的解.
板书设计
课题:5.1.1 一元一次方程
教师板演区
学生展示区
一、方程的定义.
二、一元一次方程的定义
三、方程的解.
四、列一元一次方程
作业布置
课本 P132 习题5.1
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
