高中数学必修第一册人教A版(2019)5.1.2《弧度制》名师 课件(共34张PPT)
文档属性
| 名称 | 高中数学必修第一册人教A版(2019)5.1.2《弧度制》名师 课件(共34张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-08 15:31:46 | ||
图片预览











文档简介
(共34张PPT)
1米是 秒的时间内光在真空中行驶的长度
1千克是1立方米的纯水在4℃时的质量
复习引入
思考:请说出下列的∠AOB大小.
180°
90°
A
O
B
360°
A
O
B
A
O
B
A
O
(B)
A
O
角度制
(1)角度制规定:将一个圆周分成_____份,每一份叫做___度的角( ). 故一周等于____度( ),平角等于_____度( ),直角等于_____度( )
(2)角度制的单位是度、分、秒,它们是_____进制.
360
1
1°
360
360°
180
180°
90
90°
60
(用“度”作为单位来度量角的单位制.)
复习引入
60°
A
O
A
O
B
A
O
问题:除了角度制,还有哪种单位制可以度量角的大小呢?
复习引入
人教A版同步教材名师课件
弧度制
学习目标
学 习 目 标 核心素养
了解角的另外一种度量方法——弧度制 数学抽象
能够熟练地进行角度制和弧度制之间的换算 数学运算
掌握弧度制中扇形的弧长公式和面积公式 逻辑推理
课程目标
1.了解弧度制,明确1弧度的含义.
2.能进行弧度与角度的互化.
3.掌握用弧度制表示扇形的弧长公式和面积公式.
数学学科素养
1.数学抽象:理解弧度制的概念;
2.逻辑推理:用弧度制表示角的集合;
3.直观想象:区域角的表示;
4.数学运算:运用已知条件处理扇形有关问题.
学习目标
o
A
为了使用方便,数学上还采用另一种度量角的单位制 弧度制.
弧度概念:
把长度等于半径长的弧所对的圆心角叫做1弧度的角.
B
1rad
1
可以证明,一定大小的圆心角a所对的弧长与半径的比值是唯一确定的,与半径大小无关.
即一个角的弧度数是一个与圆的半径大小无关的量.
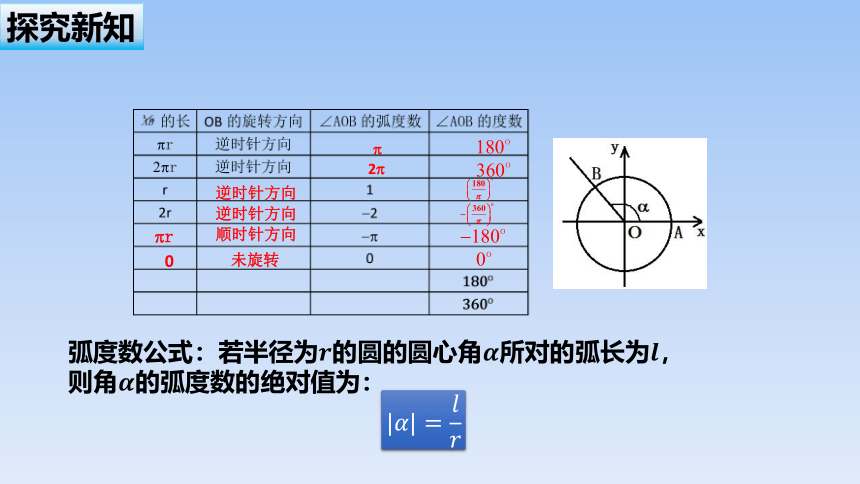
探究新知
角可以用度为单位进行度量,1度的角等于周角的.这种用度作为单位来度
量角的单位制叫做角度制.
p
2p
逆时针方向
逆时针方向
pr
顺时针方向
0
未旋转
探究新知
弧度数公式:若半径为的圆的圆心角所对的弧长为,则角的弧度数的绝对值为:
例如:sin2 ; sin; ;sin .
性质:
正角的弧度数是一个正数,负角的弧度数是一个负数,零角的弧度数是0;
以弧度作为单位来度量角的单位制,叫做弧度制.
弧度制:
用弧度表示角的时候,“弧度”二字或“rad”可以省略.
但是要弄清其含义,不能混淆.
探究新知
那么1 rad的角到底有多大呢?角度与弧度之间怎么换算呢?
圆周角360°对应的弧长即是圆的周长2πr,由弧度的定义可知:
计算半径为r的圆周角对应的弧长,并根据弧度的定义求圆周角360°的弧度.
360°=2π rad
探究新知
由360°=2π rad,我们可以求得:
(1)180°=______ rad;
(2)1° =______ rad;
(3)_____=1 rad
π
≈57.3°
探究新知
例:(1)角的弧度是多少?
(2)角的角度是多少?
实数集R
任意角的集合
这样角的集合与实数集R之间可以建立一种一一对应的关系
正角
零角
负角
正实数
负实数
0
正角的弧度数是一个正数,负角的弧度数是一个负数,零角的弧度数是0;
探究新知
根据度与弧度的换算关系,填写下表中特殊角的度数或弧度数.
角度
弧度
探究新知
典例讲解
例1、
(1)将用弧度表示出来,并指出它是第几象限角;
(2)将 用角度表示出来,并在内找出与它终边相同的所有的角.
解析
,角α是第二象限角.
则与角终边相同的角可表示为,
终边相同的角是角.
方法归纳
角度制与弧度制是两种不同的度量单位,在表示角时,角度制与弧度制不能混用.例如 的写法都是不正确的.
该题的易错点主要有两个方面:一是单位不统一,结果中角度制与弧度制混用;二是角度制与弧度制换算错误.
变式训练
1.(1)把°角写成的形式其中;
(2)在0°~720°内找出与角终边相同的角.
解析
,且
终边相同的角为
,
终边相同的角为.
典例讲解
例2、用弧度表示顶点在原点,始边与轴的非负半轴重合,终边落在图中阴影部分内的角的集合.
解析
题图①中,在内,以OB为终边的角为角,化为弧度为设终边落在题图①中阴影部分内的角为
题图②中,在内,以OB为终边的角为角,化为弧度为
,设题图②中终边落在阴影部分的角为.
方法归纳
用弧度表示区域角的解题步骤
(1)定边界角,注意实虚线的区别;
(2)化角度为弧度;
(3)确定旋转方向;
(4)用集合表示。
变式训练
2.(1)用弧度分别表示终边落在轴的非正、非负半轴上,轴的非正、非负半轴 上,轴上, 轴上的角的集合(角的顶点在原点,始边与x轴的非负半轴重合);
(2)用弧度分别表示第一、二、三、四象限角的集合。
解析
(1)终边落在轴的非正半轴上的角的集合为;
终边落在轴的非负半轴上的角的集合为;
终边落在轴的非正半轴上的角的集合为;
终边落在轴的非负半轴上的角的集合为;
终边落在轴上的角的集合为;
终边落在轴上的角的集合为
变式训练
解析
(2)第一象限角的集合为;
第二象限角的集合为
第三象限角的集合为;
第四象限角的集合为
2.(1)用弧度分别表示终边落在轴的非正、非负半轴上,轴的非正、非负半轴 上,轴上, 轴上的角的集合(角的顶点在原点,始边与x轴的非负半轴重合);
(2)用弧度分别表示第一、二、三、四象限角的集合。
变式训练
3.用弧度表示终边落在图中阴影部分内的角的集合.
解析
终边落在题图①中阴影部分内的角的集合为.
终边落在题图②中阴影部分内的角的集合为.
终边落在题图③中阴影部分内的角的集合为
注:扇形的面积公式中的角都用弧度数,不能用度数
例3、利用弧度制证明下列关于扇形的公式:
.
其中是圆的半径,是弧长,为圆心角,是扇形的面积.
典例讲解
证明: 公式得:
由于半径为R,圆心角为扇形的弧长公式和面积公式分别为:
将转换为弧度,得:
将代入上式,即得.
典例讲解
例4、已知扇形的周长为20cm,当它的半径和圆心角各取什么值时,才能使扇形的面积最大?最大面积是多少?
解析
设扇形的半径为,弧长为,面积为.
扇形的面积最大,为25cm2,
此时
当扇形的半径为5cm,圆心角为2rad时,它的面积最大,最大面积为25cm2.
方法归纳
解决扇形的弧长或面积的最值问题的关键是运用函数思想,转化为求函数的最值问题即可
变式训练
4.已知扇形的圆心角为,所在圆的半径为
(1)若,求扇形的弧长;
(2)若扇形的周长为24,当为多少弧度时,该扇形的面积S最大?并求出最大面积。
解析
(1)
(2),
所以当时,S有最大值,最大值为36,此时
即当α=2时,S取得最大值,最大值为36.
典例讲解
例5、如图所示,一绳索绕在半径为40厘米的滑轮上,绳索的下端B处悬挂着物体W,如果轮子按逆时针方向每分钟匀速旋转6圈,那么需要经过几秒钟才能使物体W向上升高100厘米?
解析
设需要秒才能使物体W向上升高100厘米
厘米
厘米,所对的圆心角
轮子每分钟匀速旋转6圈, 每秒钟匀速转过,即秒转过弧度.
,解得大约需要经过4秒钟才能使物体W向上升高100厘米.
方法归纳
在实际生活中,滑轮是一种重要的省力工具,单个滑轮转动时,滑轮上的点转过的弧长与跟它连接的绳索上的点移动的距离是相等的。
变式训练
5.工艺扇面是中国书画一种常见的表现形式高一某班学生想用布料制作一面如图所示的扇面参加元旦晚会已知此扇面的圆心角为60°,外圆半径为60cm,内圆半径为30cm,则制作这样一面扇面需要的布料面积为______cm2。
解析
由扇形的面积公式,可得制作这样面扇面需要的布料为
变式训练
6.如图,某公路交叉处的周围呈扇形形状,某市规划局拟在这块扇形土地上修建一个圆形广场已知的长度为,怎样设计能使广场的占地面积最大?最大值是多少?
连接,
,,解得=100.
这时的面积为
故当是扇形AOB的内切圆时,广场占地面积最大,最大值为.
解析
的长度为,
,根据题意可知当是扇形AOB的内切圆时,广场占地面积最大,此时OA切于点C.
1.释疑弧长公式及扇形的面积公式
(1)公式中共四个量分别为α,l,r,S,由其中的两个量可以求出另外的两个量,即知二求二.
(2)运用弧度制下的弧长公式及扇形的面积公式明显比角度制下的公式简单得多,但要注意它的前提是α为弧度制.
素养提炼
2.角度制与弧度制的比较
角 度 制 用度作为单位来度量角的单位制 角的大小与半径无关 单位“°”不能省略 角的正负与方向有关 六十进制
弧 度 制 用弧度作为单位来度量角的单位制 角的大小与半径无关 单位“rad”可以省略 角的正负与方向有关 十进制
素养提炼
当堂练习
1、下列命题中,错误的是( )
A. “度”与“弧度”是度量角的两种不同的度量单位
B.的角是周角的的角是周角的
C. 1rad的角比的角要大
D. 用弧度制度量角时,角的大小与圆的半径有关
2 、 60°的弧度数是( )
3 、在范围内,与角终边相同的角是( )
4 、半径为πcm,中心角为120°的弧长为( )
D
C
D
归纳小结
弧度制
弧度
角度与弧度的互化
角度化为弧度
孤度化为角度
特殊角的弧度数
弧长公式与扇形面积公式
作 业
P175练习:1、2、6
1米是 秒的时间内光在真空中行驶的长度
1千克是1立方米的纯水在4℃时的质量
复习引入
思考:请说出下列的∠AOB大小.
180°
90°
A
O
B
360°
A
O
B
A
O
B
A
O
(B)
A
O
角度制
(1)角度制规定:将一个圆周分成_____份,每一份叫做___度的角( ). 故一周等于____度( ),平角等于_____度( ),直角等于_____度( )
(2)角度制的单位是度、分、秒,它们是_____进制.
360
1
1°
360
360°
180
180°
90
90°
60
(用“度”作为单位来度量角的单位制.)
复习引入
60°
A
O
A
O
B
A
O
问题:除了角度制,还有哪种单位制可以度量角的大小呢?
复习引入
人教A版同步教材名师课件
弧度制
学习目标
学 习 目 标 核心素养
了解角的另外一种度量方法——弧度制 数学抽象
能够熟练地进行角度制和弧度制之间的换算 数学运算
掌握弧度制中扇形的弧长公式和面积公式 逻辑推理
课程目标
1.了解弧度制,明确1弧度的含义.
2.能进行弧度与角度的互化.
3.掌握用弧度制表示扇形的弧长公式和面积公式.
数学学科素养
1.数学抽象:理解弧度制的概念;
2.逻辑推理:用弧度制表示角的集合;
3.直观想象:区域角的表示;
4.数学运算:运用已知条件处理扇形有关问题.
学习目标
o
A
为了使用方便,数学上还采用另一种度量角的单位制 弧度制.
弧度概念:
把长度等于半径长的弧所对的圆心角叫做1弧度的角.
B
1rad
1
可以证明,一定大小的圆心角a所对的弧长与半径的比值是唯一确定的,与半径大小无关.
即一个角的弧度数是一个与圆的半径大小无关的量.
探究新知
角可以用度为单位进行度量,1度的角等于周角的.这种用度作为单位来度
量角的单位制叫做角度制.
p
2p
逆时针方向
逆时针方向
pr
顺时针方向
0
未旋转
探究新知
弧度数公式:若半径为的圆的圆心角所对的弧长为,则角的弧度数的绝对值为:
例如:sin2 ; sin; ;sin .
性质:
正角的弧度数是一个正数,负角的弧度数是一个负数,零角的弧度数是0;
以弧度作为单位来度量角的单位制,叫做弧度制.
弧度制:
用弧度表示角的时候,“弧度”二字或“rad”可以省略.
但是要弄清其含义,不能混淆.
探究新知
那么1 rad的角到底有多大呢?角度与弧度之间怎么换算呢?
圆周角360°对应的弧长即是圆的周长2πr,由弧度的定义可知:
计算半径为r的圆周角对应的弧长,并根据弧度的定义求圆周角360°的弧度.
360°=2π rad
探究新知
由360°=2π rad,我们可以求得:
(1)180°=______ rad;
(2)1° =______ rad;
(3)_____=1 rad
π
≈57.3°
探究新知
例:(1)角的弧度是多少?
(2)角的角度是多少?
实数集R
任意角的集合
这样角的集合与实数集R之间可以建立一种一一对应的关系
正角
零角
负角
正实数
负实数
0
正角的弧度数是一个正数,负角的弧度数是一个负数,零角的弧度数是0;
探究新知
根据度与弧度的换算关系,填写下表中特殊角的度数或弧度数.
角度
弧度
探究新知
典例讲解
例1、
(1)将用弧度表示出来,并指出它是第几象限角;
(2)将 用角度表示出来,并在内找出与它终边相同的所有的角.
解析
,角α是第二象限角.
则与角终边相同的角可表示为,
终边相同的角是角.
方法归纳
角度制与弧度制是两种不同的度量单位,在表示角时,角度制与弧度制不能混用.例如 的写法都是不正确的.
该题的易错点主要有两个方面:一是单位不统一,结果中角度制与弧度制混用;二是角度制与弧度制换算错误.
变式训练
1.(1)把°角写成的形式其中;
(2)在0°~720°内找出与角终边相同的角.
解析
,且
终边相同的角为
,
终边相同的角为.
典例讲解
例2、用弧度表示顶点在原点,始边与轴的非负半轴重合,终边落在图中阴影部分内的角的集合.
解析
题图①中,在内,以OB为终边的角为角,化为弧度为设终边落在题图①中阴影部分内的角为
题图②中,在内,以OB为终边的角为角,化为弧度为
,设题图②中终边落在阴影部分的角为.
方法归纳
用弧度表示区域角的解题步骤
(1)定边界角,注意实虚线的区别;
(2)化角度为弧度;
(3)确定旋转方向;
(4)用集合表示。
变式训练
2.(1)用弧度分别表示终边落在轴的非正、非负半轴上,轴的非正、非负半轴 上,轴上, 轴上的角的集合(角的顶点在原点,始边与x轴的非负半轴重合);
(2)用弧度分别表示第一、二、三、四象限角的集合。
解析
(1)终边落在轴的非正半轴上的角的集合为;
终边落在轴的非负半轴上的角的集合为;
终边落在轴的非正半轴上的角的集合为;
终边落在轴的非负半轴上的角的集合为;
终边落在轴上的角的集合为;
终边落在轴上的角的集合为
变式训练
解析
(2)第一象限角的集合为;
第二象限角的集合为
第三象限角的集合为;
第四象限角的集合为
2.(1)用弧度分别表示终边落在轴的非正、非负半轴上,轴的非正、非负半轴 上,轴上, 轴上的角的集合(角的顶点在原点,始边与x轴的非负半轴重合);
(2)用弧度分别表示第一、二、三、四象限角的集合。
变式训练
3.用弧度表示终边落在图中阴影部分内的角的集合.
解析
终边落在题图①中阴影部分内的角的集合为.
终边落在题图②中阴影部分内的角的集合为.
终边落在题图③中阴影部分内的角的集合为
注:扇形的面积公式中的角都用弧度数,不能用度数
例3、利用弧度制证明下列关于扇形的公式:
.
其中是圆的半径,是弧长,为圆心角,是扇形的面积.
典例讲解
证明: 公式得:
由于半径为R,圆心角为扇形的弧长公式和面积公式分别为:
将转换为弧度,得:
将代入上式,即得.
典例讲解
例4、已知扇形的周长为20cm,当它的半径和圆心角各取什么值时,才能使扇形的面积最大?最大面积是多少?
解析
设扇形的半径为,弧长为,面积为.
扇形的面积最大,为25cm2,
此时
当扇形的半径为5cm,圆心角为2rad时,它的面积最大,最大面积为25cm2.
方法归纳
解决扇形的弧长或面积的最值问题的关键是运用函数思想,转化为求函数的最值问题即可
变式训练
4.已知扇形的圆心角为,所在圆的半径为
(1)若,求扇形的弧长;
(2)若扇形的周长为24,当为多少弧度时,该扇形的面积S最大?并求出最大面积。
解析
(1)
(2),
所以当时,S有最大值,最大值为36,此时
即当α=2时,S取得最大值,最大值为36.
典例讲解
例5、如图所示,一绳索绕在半径为40厘米的滑轮上,绳索的下端B处悬挂着物体W,如果轮子按逆时针方向每分钟匀速旋转6圈,那么需要经过几秒钟才能使物体W向上升高100厘米?
解析
设需要秒才能使物体W向上升高100厘米
厘米
厘米,所对的圆心角
轮子每分钟匀速旋转6圈, 每秒钟匀速转过,即秒转过弧度.
,解得大约需要经过4秒钟才能使物体W向上升高100厘米.
方法归纳
在实际生活中,滑轮是一种重要的省力工具,单个滑轮转动时,滑轮上的点转过的弧长与跟它连接的绳索上的点移动的距离是相等的。
变式训练
5.工艺扇面是中国书画一种常见的表现形式高一某班学生想用布料制作一面如图所示的扇面参加元旦晚会已知此扇面的圆心角为60°,外圆半径为60cm,内圆半径为30cm,则制作这样一面扇面需要的布料面积为______cm2。
解析
由扇形的面积公式,可得制作这样面扇面需要的布料为
变式训练
6.如图,某公路交叉处的周围呈扇形形状,某市规划局拟在这块扇形土地上修建一个圆形广场已知的长度为,怎样设计能使广场的占地面积最大?最大值是多少?
连接,
,,解得=100.
这时的面积为
故当是扇形AOB的内切圆时,广场占地面积最大,最大值为.
解析
的长度为,
,根据题意可知当是扇形AOB的内切圆时,广场占地面积最大,此时OA切于点C.
1.释疑弧长公式及扇形的面积公式
(1)公式中共四个量分别为α,l,r,S,由其中的两个量可以求出另外的两个量,即知二求二.
(2)运用弧度制下的弧长公式及扇形的面积公式明显比角度制下的公式简单得多,但要注意它的前提是α为弧度制.
素养提炼
2.角度制与弧度制的比较
角 度 制 用度作为单位来度量角的单位制 角的大小与半径无关 单位“°”不能省略 角的正负与方向有关 六十进制
弧 度 制 用弧度作为单位来度量角的单位制 角的大小与半径无关 单位“rad”可以省略 角的正负与方向有关 十进制
素养提炼
当堂练习
1、下列命题中,错误的是( )
A. “度”与“弧度”是度量角的两种不同的度量单位
B.的角是周角的的角是周角的
C. 1rad的角比的角要大
D. 用弧度制度量角时,角的大小与圆的半径有关
2 、 60°的弧度数是( )
3 、在范围内,与角终边相同的角是( )
4 、半径为πcm,中心角为120°的弧长为( )
D
C
D
归纳小结
弧度制
弧度
角度与弧度的互化
角度化为弧度
孤度化为角度
特殊角的弧度数
弧长公式与扇形面积公式
作 业
P175练习:1、2、6
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
