第24章《圆》单元测试卷(含答案)
图片预览




文档简介
中小学教育资源及组卷应用平台
2022年九年级上《圆》单元复习卷
一、选择题:(本大题有12小题,每小题3分,满分36分)
1.(3分)在平面直角坐标系中,以点(2,1)为圆心,1为半径的圆,必与( )
A.x轴相交 B.y轴相交 C.x轴相切 D.y轴相切
2.(3分)如果两圆的半径分别为3和4,圆心距为3,那么这两个圆的位置关系是( )
A.外离 B.外切 C.相交 D.内切
3.(3分)圆锥的侧面展开图是一个半圆,则这个圆锥的母线长与底面半径的比是( )
A.2:1 B.2π:1 C.:1 D.:1
4.(3分)两圆的半径分别是R、r(R>r),圆心距为d,且有等式R2+r2﹣d2=2Rr成立,则这两圆的位置关系是( )
A.相交 B.外切 C.内切 D.外切或内切
5.(3分)如图,⊙O的直径为10 cm,弦AB垂直平分半径OC,则弦AB长为( )
A.2.5cm B.5cm C.5cm D.10cm
6.(3分)⊙O和⊙P相交于A、B两点,且两圆半径分别为5和4,公共弦AB=6,则OP=( )
A.4+ B.9 C.4﹣ D.4±
7.(3分)如图,正方形的边长为a,以各边为直径在正方形内画半圆,则阴影部分的面积为( )
A.a2﹣a2 B.a2﹣a2 C.a2﹣a2 D.πa2﹣a2
8.(3分)小华想用一个圆心角为120°,半径为6cm的扇形做一个圆锥的侧面(接缝忽略不计),则做成的圆锥底面半径为( )
A.4cm B.3cm C.2cm D.1cm
9.(3分)如图,A,B是⊙O上的两点,AC是⊙O的切线,∠B=70°,则∠BAC等于( )
A.70° B.35° C.20° D.10°
10.(3分)如图,PA、PB是⊙O的切线,切点分别为A、B,点C在⊙O上,如果∠P=50°,那么∠ACB等于( )
A.40° B.50° C.65° D.130°
11.(3分)下列命题中,为真命题的是( )
A.长度相等的弧所对的圆心角相等
B.垂直于圆的半径的直线是该圆的切线
C.过弦的中点的直线必过圆心
D.三角形的外心到三个顶点的距离相等
12.(3分)已知P为边长是2的正六边形ABCDEF内一点,P点到各边的距离分别为h1、h2、h3 h4、h5、h6,则h1+h2+h3+h4+h5+h6=( )
A.2 B.4 C.6 D.8
二、填空题:(本大题有6小题,每小题4分,满分24分)
13.(4分)两圆的半径比是5:3,外切时圆心距是32cm,当两圆内切时,圆心距为 cm.
14.(4分)如图,一扇形纸扇完全打开后,外侧两竹条AB和AC的夹角为120°,AB长为30cm,贴纸部分的宽为20cm,则贴纸部分的面积为 cm2.
15.(4分)半径分别为4和5的相交两圆所成的公共弦长为6,则两圆的圆心距为 .
16.(4分)在半径为5cm的⊙O中,如果弦CD=8cm,直径AB⊥CD,垂足为E,则AE的长为 cm.
17.(4分)如图,已知AB是⊙O的弦,P是AB上一点,若AB=10cm,PB=4cm,OP=5cm,则⊙O的半径等于 cm.
18.(4分)如图,A,B,C是⊙O上三点,当BC平分∠ABO时,能得出结论: (任写一个).
三、解答题
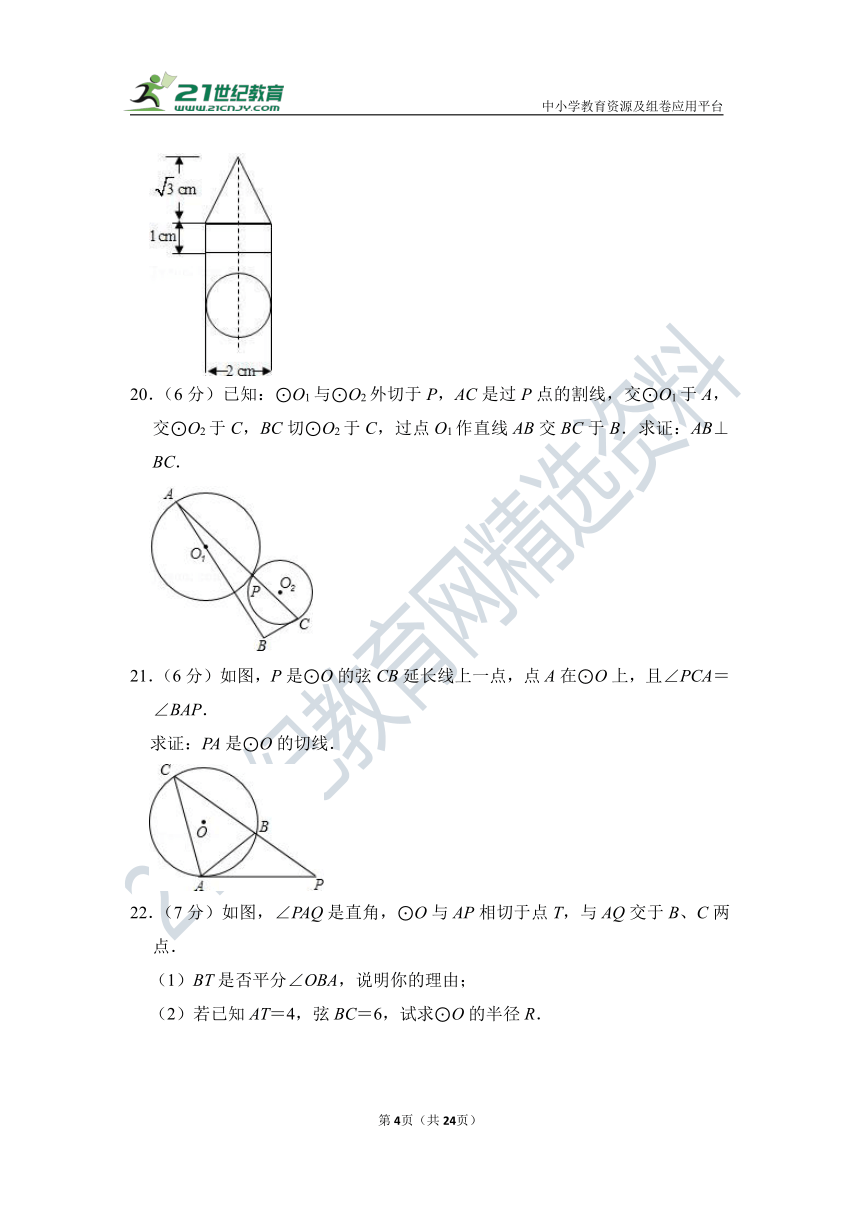
19.(5分)附加题:如图是某工件的二视图,按图中尺寸求工件的表面积.
20.(6分)已知:⊙O1与⊙O2外切于P,AC是过P点的割线,交⊙O1于A,交⊙O2于C,BC切⊙O2于C,过点O1作直线AB交BC于B.求证:AB⊥BC.
21.(6分)如图,P是⊙O的弦CB延长线上一点,点A在⊙O上,且∠PCA=∠BAP.
求证:PA是⊙O的切线.
22.(7分)如图,∠PAQ是直角,⊙O与AP相切于点T,与AQ交于B、C两点.
(1)BT是否平分∠OBA,说明你的理由;
(2)若已知AT=4,弦BC=6,试求⊙O的半径R.
23.(7分)如图,一块直角三角板形状的木板余料,木工师傅要在此余料上锯出一块圆形的木板制作凳面,要想使锯出的凳面的面积最大
(1)请你试着用直尺和圆规画出此圆(要求尺规作图,保留作图痕迹,不写作法).
(2)若此Rt△ABC的直角边分别为30cm和40cm,试求此圆凳面的面积.
24.(6分)如图,已知⊙O的半径为R,直径AB⊥CD以B为圆心,以BC为半径作弧CED.求弧CED与弧CAD围成的新月形ACED的面积S.
25.(7分)如图,在一个横截面为Rt△ABC的物体中,∠CAB=30°,BC=1米.工人师傅把此物体搬到墙边,先将AB边放在地面(直线l)上,再按顺时针方向绕点B翻转到△A1B1C1的位置(BC1在l上),最后沿BC1的方向移到△A2B2C2的位置,其平移的距离为线段AC的长度(此时A2C2恰好靠在墙边).
(1)请直接写出AB、AC的长;
(2)画出在搬动此物的整个过程A点所经过的路径,并求出该路径的长度(精确到0.1米).
26.(6分)如图,AB为⊙O直径,自圆上一点P作AB的垂线PH,垂足为H,自点A向过P点的切线作垂线,垂足为K.求证:AH=AK.
27.(10分)已知:如图,AB是⊙O的一条弦,点C为的中点,CD是⊙O的直径,过C点的直线l交AB所在直线于点E,交⊙O于点F.
(1)判定图中∠CEB与∠FDC的数量关系,并写出结论;
(2)将直线l绕C点旋转(与CD不重合),在旋转过程中,E点,F点的位置也随之变化,请你在下面两个备用图中分别画出在不同位置时,使(1)的结论仍然成立的图形,标上相应字母,选其中一个图形给予证明.
2022年九年级上《圆》单元复习卷
参考答案与试题解析
一、选择题:(本大题有12小题,每小题3分,满分36分)
1.(3分)在平面直角坐标系中,以点(2,1)为圆心,1为半径的圆,必与( )
A.x轴相交 B.y轴相交 C.x轴相切 D.y轴相切
【解答】解:∵是以点(2,1)为圆心,1为半径的圆,
∴圆心到x轴的距离是1,圆心到y轴的距离是2,则1=1,1<2,
∴该圆必与y轴相离,与x轴相切.故选C.
2.(3分)如果两圆的半径分别为3和4,圆心距为3,那么这两个圆的位置关系是( )
A.外离 B.外切 C.相交 D.内切
【解答】解:∵两圆的半径分别为3和4,圆心距为3,
又∵3+4=7,4﹣3=1,1<3<7,
∴这两个圆的位置关系是相交.
故选:C.
3.(3分)圆锥的侧面展开图是一个半圆,则这个圆锥的母线长与底面半径的比是( )
A.2:1 B.2π:1 C.:1 D.:1
【解答】解:设底面半径为r,母线长为R,则底面周长=2πr=×2πR,∴R:r=2:1.
故选:A.
4.(3分)两圆的半径分别是R、r(R>r),圆心距为d,且有等式R2+r2﹣d2=2Rr成立,则这两圆的位置关系是( )
A.相交 B.外切 C.内切 D.外切或内切
【解答】解:∵R2+r2﹣d2=2Rr,
∴R2+r2﹣2Rr=d2,
∴(R﹣r)2=d2,
∴d=|R﹣r|,
∵两圆的半径分别是R、r(R>r),圆心距为d,
∴这两圆的位置关系是:内切.
故选:C.
5.(3分)如图,⊙O的直径为10 cm,弦AB垂直平分半径OC,则弦AB长为( )
A.2.5cm B.5cm C.5cm D.10cm
【解答】解:设AB与OC交于点M,
在直角△OAM中,OA=5cm,OM=2.5cm,
根据勾股定理得到:AM=2.5cm.因而AB=2AM=5cm.
故选:C.
6.(3分)⊙O和⊙P相交于A、B两点,且两圆半径分别为5和4,公共弦AB=6,则OP=( )
A.4+ B.9 C.4﹣ D.4±
【解答】解:分为两种情况:
①
连接OA、PA、OP,OP交AB于C,
∵AB是⊙O和⊙P的公共弦,
∴OP⊥AB,
∴∠ACO=∠ACP=90°,
由垂径定理得:AC=BC=×6=3,
由勾股定理得:OC===4,
CP==,
∴OP=OC+CP=4+;
②如图2,
由①知:CP=,OC=4,
∴OP=4﹣,
故选:D.
7.(3分)如图,正方形的边长为a,以各边为直径在正方形内画半圆,则阴影部分的面积为( )
A.a2﹣a2 B.a2﹣a2 C.a2﹣a2 D.πa2﹣a2
【解答】解:由图象可以看出,
4个相同阴影部分的面积=四个半圆的面积﹣正方形的面积=﹣a2,
∴题中阴影部分面积为,
故选:A.
8.(3分)小华想用一个圆心角为120°,半径为6cm的扇形做一个圆锥的侧面(接缝忽略不计),则做成的圆锥底面半径为( )
A.4cm B.3cm C.2cm D.1cm
【解答】解:设底面半径为Rcm,则底面周长=2Rπcm,侧面面积=×2Rπ×6=,∴R=2cm.
故选:C.
9.(3分)如图,A,B是⊙O上的两点,AC是⊙O的切线,∠B=70°,则∠BAC等于( )
A.70° B.35° C.20° D.10°
【解答】解:∵OA=OB,
∴∠B=∠OAB=70°,
∵AC是⊙O的切线,
∴OA⊥AC,
则∠BAC=20°.
故选:C.
10.(3分)如图,PA、PB是⊙O的切线,切点分别为A、B,点C在⊙O上,如果∠P=50°,那么∠ACB等于( )
A.40° B.50° C.65° D.130°
【解答】解:连接OA,OB.
根据切线的性质,得∠OBP=∠OAP=90°,
根据四边形的内角和定理得∠AOB=130°,
再根据圆周角定理得∠C=∠AOB=65°.
故选:C.
11.(3分)下列命题中,为真命题的是( )
A.长度相等的弧所对的圆心角相等
B.垂直于圆的半径的直线是该圆的切线
C.过弦的中点的直线必过圆心
D.三角形的外心到三个顶点的距离相等
【解答】解:A、长度相等的弧不一定是等弧,错误;
B、应经过半径的外端.错误;
C、垂径定理及其推论是知二推三,少一个条件,错误;
D、正确.
故选:D.
12.(3分)已知P为边长是2的正六边形ABCDEF内一点,P点到各边的距离分别为h1、h2、h3 h4、h5、h6,则h1+h2+h3+h4+h5+h6=( )
A.2 B.4 C.6 D.8
【解答】解:如图所示,
∵P为边长是2的正六边形ABCDEF内一点,P点到各边的距离分别为h1、h2、h3 h4、h5、h6,
∴S正六边形ABCDEF=×2(h1+h2+h3+h4+h5+h6),
过正六边形的中心O作OG⊥BC于点G,则S正六边形ABCDEF=6××2OG=6OG,
∴h1+h2+h3+h4+h5+h6=6OG,
∵∠OBC=60°,OG⊥BC,
∴BG=BC=2,OG=BG tan60°=1×=,
∴h1+h2+h3+h4+h5+h6=6OG=6×=6.
故选:C.
二、填空题:(本大题有6小题,每小题4分,满分24分)
13.(4分)两圆的半径比是5:3,外切时圆心距是32cm,当两圆内切时,圆心距为 8 cm.
【解答】解:设大圆的半径为R,小圆的半径为r,则有
R:r=5:3;
又因为R+r=32,
解得R=20,r=12,
故当它们内切时,圆心距=20﹣12=8(cm).
故答案为:8.
14.(4分)如图,一扇形纸扇完全打开后,外侧两竹条AB和AC的夹角为120°,AB长为30cm,贴纸部分的宽为20cm,则贴纸部分的面积为 cm2.
【解答】解:S=﹣=cm2.
15.(4分)半径分别为4和5的相交两圆所成的公共弦长为6,则两圆的圆心距为 4+或4﹣ .
【解答】解:根据相交两圆的连心线垂直平分两圆的公共弦,得弦的一半是3,
分别运用勾股定理计算,
连心线和弦的交点到两个圆心的距离是和4,
如果公共弦在两个圆心之间,则圆心距是4+,
如果公共弦在两圆圆心的外部,则圆心距是4﹣.
16.(4分)在半径为5cm的⊙O中,如果弦CD=8cm,直径AB⊥CD,垂足为E,则AE的长为 2或8 cm.
【解答】解:(1)因为直径AB⊥CD,所以CE=ED=8×=4cm,
因为半径为5cm,所以在直角三角形中,
OE===3cm,
AE=5+3=8cm;
(2)将A、B改变位置,即可得到AE=5﹣3=2cm.
因此,AE的长为2cm或8cm.
17.(4分)如图,已知AB是⊙O的弦,P是AB上一点,若AB=10cm,PB=4cm,OP=5cm,则⊙O的半径等于 7 cm.
【解答】解:将OP向两方延长,
设OC=xcm,则CP=(x+5)cm,PD=(x﹣5)cm,
根据相交弦定理,AP BP=CP DP,即(10﹣4)×4=(x+5)(x﹣5),
解得x2=49,x=7或x=﹣7(负值舍去),
则⊙O的半径等于7cm.
18.(4分)如图,A,B,C是⊙O上三点,当BC平分∠ABO时,能得出结论: AB∥OC (任写一个).
【解答】解:∵A,B,C是⊙O上三点,当BC平分∠ABO时,
∴∠CBO=∠CBA.
∵OB=OC,
∴∠OCB=∠OBC.
∴∠CBA=∠OCB.
∴AB∥OC.
三、解答题
19.(5分)附加题:如图是某工件的二视图,按图中尺寸求工件的表面积.
【解答】解:由二视图得:圆柱的底面半径为r=1cm,圆柱的高为h1=1cm,
圆锥的底面半径r=1cm,圆锥高,则圆柱的侧面积S圆柱侧=2πrh1=2π(cm2),
圆柱的底面积S=πr2=π(cm2),
又圆锥的母线,∴圆锥的侧面积S圆锥侧=πrl=2π(cm2).
∴此工件的表面积为S表=S圆柱侧+S圆锥侧+S=5π(cm2).
20.(6分)已知:⊙O1与⊙O2外切于P,AC是过P点的割线,交⊙O1于A,交⊙O2于C,BC切⊙O2于C,过点O1作直线AB交BC于B.求证:AB⊥BC.
【解答】解:连接O1O2,O2C,
∵BC切⊙O2于C,
∴O2C⊥BC,
∵O1O2连接线经过P,
∴AO1=O1P,O2P=O2C,
又∵∠O1PA=∠O2PC,
∴∠PAO1=∠O1PA=∠O2PC=∠O2CP,
∴AB∥O2C,
∴AB⊥BC.
21.(6分)如图,P是⊙O的弦CB延长线上一点,点A在⊙O上,且∠PCA=∠BAP.
求证:PA是⊙O的切线.
【解答】证明:作⊙O的直径AD,连接BD.
则∠C=∠D(同弧所对的圆周角相等),∠ABD=90°(直径所对的圆周角是直角),
∴∠D+∠BAD=90°,
∴∠C+∠BAD=90°(等量代换);
又∵∠PCA=∠BAP,
∴∠BAD+∠PAB=90°,即AP⊥AD,
∴PA是⊙O的切线.
22.(7分)如图,∠PAQ是直角,⊙O与AP相切于点T,与AQ交于B、C两点.
(1)BT是否平分∠OBA,说明你的理由;
(2)若已知AT=4,弦BC=6,试求⊙O的半径R.
【解答】(1)BT平分∠OBA,理由为:
证明:连接OT,如图所示,
∵AP与圆O相切,
∴OT⊥AP,
∴∠OTP=90°,
又∠QAP=90°,
∴∠OTP=∠QAP,
∴OT∥QA,
∴∠OTB=∠ABT,
又∵OB=OT,
∴∠OBT=∠OTB,
∴∠OBT=∠ABT,
则BT平分∠OBA;
(2)解:过O作OD⊥BC,又BC=6,
可得D为BC的中点,即BD=CD=3,
∵四边形ODAT为矩形,
∴OD=AT=4,
在Rt△OBD中,BD=3,OD=4,
根据勾股定理得:OB==5,
则圆的半径为5.
23.(7分)如图,一块直角三角板形状的木板余料,木工师傅要在此余料上锯出一块圆形的木板制作凳面,要想使锯出的凳面的面积最大
(1)请你试着用直尺和圆规画出此圆(要求尺规作图,保留作图痕迹,不写作法).
(2)若此Rt△ABC的直角边分别为30cm和40cm,试求此圆凳面的面积.
【解答】解:(1)如图所示:
(2)设三角形内切圆半径为r,则
r (50+40+30)=×30×40,
解得:r=10(cm).
故此圆凳面的面积为:π×102=100π(cm 2).
24.(6分)如图,已知⊙O的半径为R,直径AB⊥CD以B为圆心,以BC为半径作弧CED.求弧CED与弧CAD围成的新月形ACED的面积S.
【解答】解:∵CD⊥BA,OC=OD=OB,
∴△BCD是等腰直角三角形,CB⊥BD,BC=R.
∴S阴影=S半圆CDA﹣S扇形BCD+S△BCD=πR2﹣π (R)2+×(R)2=R2.
25.(7分)如图,在一个横截面为Rt△ABC的物体中,∠CAB=30°,BC=1米.工人师傅把此物体搬到墙边,先将AB边放在地面(直线l)上,再按顺时针方向绕点B翻转到△A1B1C1的位置(BC1在l上),最后沿BC1的方向移到△A2B2C2的位置,其平移的距离为线段AC的长度(此时A2C2恰好靠在墙边).
(1)请直接写出AB、AC的长;
(2)画出在搬动此物的整个过程A点所经过的路径,并求出该路径的长度(精确到0.1米).
【解答】解:(1)∵∠CAB=30°,BC=1米
∴AB=2米,AC=米(4分).
(2)画出A点经过的路径:(5分)
∵∠ABA1=180°﹣60°=120°,A1A2=AC=米
∴A点所经过的路径长=+(7分)
=π+≈5.9(米)(8分).
26.(6分)如图,AB为⊙O直径,自圆上一点P作AB的垂线PH,垂足为H,自点A向过P点的切线作垂线,垂足为K.求证:AH=AK.
【解答】证明:连接OP,过点O作OC⊥AK于点C,
∴∠OCK=90°,
∵PK是⊙O的切线,AK⊥PK,
∴∠OPK=∠PKC=90°,
∴四边形OCKP是矩形,
∴OP=CK,AK∥OP,
∴∠A=∠POH,
在△AOC和△OPH中,
,
∴△AOC≌△OPH(AAS),
∴AC=OH,
∵AK=AC+CK,AH=OA+OH=OP+OH,
∴AH=AK.
27.(10分)已知:如图,AB是⊙O的一条弦,点C为的中点,CD是⊙O的直径,过C点的直线l交AB所在直线于点E,交⊙O于点F.
(1)判定图中∠CEB与∠FDC的数量关系,并写出结论;
(2)将直线l绕C点旋转(与CD不重合),在旋转过程中,E点,F点的位置也随之变化,请你在下面两个备用图中分别画出在不同位置时,使(1)的结论仍然成立的图形,标上相应字母,选其中一个图形给予证明.
【解答】(1)解:∠CEB=∠FDC;
理由:∵CD是⊙O的直径,点C为的中点,
∴CD⊥AB,
∴∠CEB+∠ECD=90°,
∵CD是⊙O的直径,
∴∠CFD=90°.
∴∠FDC+∠ECD=90°.
∴∠CEB=∠FDC.
(2)证明:如图②
∵CD是⊙O的直径,点C为的中点,
∴CD⊥AB,
∴∠CEB+∠ECD=90°,
∵CD是⊙O的直径,
∴∠CFD=90°.
∴∠FDC+∠ECD=90°.
∴∠CEB=∠FDC.
443576
13
第1页(共1页)
2022年九年级上《圆》单元复习卷
一、选择题:(本大题有12小题,每小题3分,满分36分)
1.(3分)在平面直角坐标系中,以点(2,1)为圆心,1为半径的圆,必与( )
A.x轴相交 B.y轴相交 C.x轴相切 D.y轴相切
2.(3分)如果两圆的半径分别为3和4,圆心距为3,那么这两个圆的位置关系是( )
A.外离 B.外切 C.相交 D.内切
3.(3分)圆锥的侧面展开图是一个半圆,则这个圆锥的母线长与底面半径的比是( )
A.2:1 B.2π:1 C.:1 D.:1
4.(3分)两圆的半径分别是R、r(R>r),圆心距为d,且有等式R2+r2﹣d2=2Rr成立,则这两圆的位置关系是( )
A.相交 B.外切 C.内切 D.外切或内切
5.(3分)如图,⊙O的直径为10 cm,弦AB垂直平分半径OC,则弦AB长为( )
A.2.5cm B.5cm C.5cm D.10cm
6.(3分)⊙O和⊙P相交于A、B两点,且两圆半径分别为5和4,公共弦AB=6,则OP=( )
A.4+ B.9 C.4﹣ D.4±
7.(3分)如图,正方形的边长为a,以各边为直径在正方形内画半圆,则阴影部分的面积为( )
A.a2﹣a2 B.a2﹣a2 C.a2﹣a2 D.πa2﹣a2
8.(3分)小华想用一个圆心角为120°,半径为6cm的扇形做一个圆锥的侧面(接缝忽略不计),则做成的圆锥底面半径为( )
A.4cm B.3cm C.2cm D.1cm
9.(3分)如图,A,B是⊙O上的两点,AC是⊙O的切线,∠B=70°,则∠BAC等于( )
A.70° B.35° C.20° D.10°
10.(3分)如图,PA、PB是⊙O的切线,切点分别为A、B,点C在⊙O上,如果∠P=50°,那么∠ACB等于( )
A.40° B.50° C.65° D.130°
11.(3分)下列命题中,为真命题的是( )
A.长度相等的弧所对的圆心角相等
B.垂直于圆的半径的直线是该圆的切线
C.过弦的中点的直线必过圆心
D.三角形的外心到三个顶点的距离相等
12.(3分)已知P为边长是2的正六边形ABCDEF内一点,P点到各边的距离分别为h1、h2、h3 h4、h5、h6,则h1+h2+h3+h4+h5+h6=( )
A.2 B.4 C.6 D.8
二、填空题:(本大题有6小题,每小题4分,满分24分)
13.(4分)两圆的半径比是5:3,外切时圆心距是32cm,当两圆内切时,圆心距为 cm.
14.(4分)如图,一扇形纸扇完全打开后,外侧两竹条AB和AC的夹角为120°,AB长为30cm,贴纸部分的宽为20cm,则贴纸部分的面积为 cm2.
15.(4分)半径分别为4和5的相交两圆所成的公共弦长为6,则两圆的圆心距为 .
16.(4分)在半径为5cm的⊙O中,如果弦CD=8cm,直径AB⊥CD,垂足为E,则AE的长为 cm.
17.(4分)如图,已知AB是⊙O的弦,P是AB上一点,若AB=10cm,PB=4cm,OP=5cm,则⊙O的半径等于 cm.
18.(4分)如图,A,B,C是⊙O上三点,当BC平分∠ABO时,能得出结论: (任写一个).
三、解答题
19.(5分)附加题:如图是某工件的二视图,按图中尺寸求工件的表面积.
20.(6分)已知:⊙O1与⊙O2外切于P,AC是过P点的割线,交⊙O1于A,交⊙O2于C,BC切⊙O2于C,过点O1作直线AB交BC于B.求证:AB⊥BC.
21.(6分)如图,P是⊙O的弦CB延长线上一点,点A在⊙O上,且∠PCA=∠BAP.
求证:PA是⊙O的切线.
22.(7分)如图,∠PAQ是直角,⊙O与AP相切于点T,与AQ交于B、C两点.
(1)BT是否平分∠OBA,说明你的理由;
(2)若已知AT=4,弦BC=6,试求⊙O的半径R.
23.(7分)如图,一块直角三角板形状的木板余料,木工师傅要在此余料上锯出一块圆形的木板制作凳面,要想使锯出的凳面的面积最大
(1)请你试着用直尺和圆规画出此圆(要求尺规作图,保留作图痕迹,不写作法).
(2)若此Rt△ABC的直角边分别为30cm和40cm,试求此圆凳面的面积.
24.(6分)如图,已知⊙O的半径为R,直径AB⊥CD以B为圆心,以BC为半径作弧CED.求弧CED与弧CAD围成的新月形ACED的面积S.
25.(7分)如图,在一个横截面为Rt△ABC的物体中,∠CAB=30°,BC=1米.工人师傅把此物体搬到墙边,先将AB边放在地面(直线l)上,再按顺时针方向绕点B翻转到△A1B1C1的位置(BC1在l上),最后沿BC1的方向移到△A2B2C2的位置,其平移的距离为线段AC的长度(此时A2C2恰好靠在墙边).
(1)请直接写出AB、AC的长;
(2)画出在搬动此物的整个过程A点所经过的路径,并求出该路径的长度(精确到0.1米).
26.(6分)如图,AB为⊙O直径,自圆上一点P作AB的垂线PH,垂足为H,自点A向过P点的切线作垂线,垂足为K.求证:AH=AK.
27.(10分)已知:如图,AB是⊙O的一条弦,点C为的中点,CD是⊙O的直径,过C点的直线l交AB所在直线于点E,交⊙O于点F.
(1)判定图中∠CEB与∠FDC的数量关系,并写出结论;
(2)将直线l绕C点旋转(与CD不重合),在旋转过程中,E点,F点的位置也随之变化,请你在下面两个备用图中分别画出在不同位置时,使(1)的结论仍然成立的图形,标上相应字母,选其中一个图形给予证明.
2022年九年级上《圆》单元复习卷
参考答案与试题解析
一、选择题:(本大题有12小题,每小题3分,满分36分)
1.(3分)在平面直角坐标系中,以点(2,1)为圆心,1为半径的圆,必与( )
A.x轴相交 B.y轴相交 C.x轴相切 D.y轴相切
【解答】解:∵是以点(2,1)为圆心,1为半径的圆,
∴圆心到x轴的距离是1,圆心到y轴的距离是2,则1=1,1<2,
∴该圆必与y轴相离,与x轴相切.故选C.
2.(3分)如果两圆的半径分别为3和4,圆心距为3,那么这两个圆的位置关系是( )
A.外离 B.外切 C.相交 D.内切
【解答】解:∵两圆的半径分别为3和4,圆心距为3,
又∵3+4=7,4﹣3=1,1<3<7,
∴这两个圆的位置关系是相交.
故选:C.
3.(3分)圆锥的侧面展开图是一个半圆,则这个圆锥的母线长与底面半径的比是( )
A.2:1 B.2π:1 C.:1 D.:1
【解答】解:设底面半径为r,母线长为R,则底面周长=2πr=×2πR,∴R:r=2:1.
故选:A.
4.(3分)两圆的半径分别是R、r(R>r),圆心距为d,且有等式R2+r2﹣d2=2Rr成立,则这两圆的位置关系是( )
A.相交 B.外切 C.内切 D.外切或内切
【解答】解:∵R2+r2﹣d2=2Rr,
∴R2+r2﹣2Rr=d2,
∴(R﹣r)2=d2,
∴d=|R﹣r|,
∵两圆的半径分别是R、r(R>r),圆心距为d,
∴这两圆的位置关系是:内切.
故选:C.
5.(3分)如图,⊙O的直径为10 cm,弦AB垂直平分半径OC,则弦AB长为( )
A.2.5cm B.5cm C.5cm D.10cm
【解答】解:设AB与OC交于点M,
在直角△OAM中,OA=5cm,OM=2.5cm,
根据勾股定理得到:AM=2.5cm.因而AB=2AM=5cm.
故选:C.
6.(3分)⊙O和⊙P相交于A、B两点,且两圆半径分别为5和4,公共弦AB=6,则OP=( )
A.4+ B.9 C.4﹣ D.4±
【解答】解:分为两种情况:
①
连接OA、PA、OP,OP交AB于C,
∵AB是⊙O和⊙P的公共弦,
∴OP⊥AB,
∴∠ACO=∠ACP=90°,
由垂径定理得:AC=BC=×6=3,
由勾股定理得:OC===4,
CP==,
∴OP=OC+CP=4+;
②如图2,
由①知:CP=,OC=4,
∴OP=4﹣,
故选:D.
7.(3分)如图,正方形的边长为a,以各边为直径在正方形内画半圆,则阴影部分的面积为( )
A.a2﹣a2 B.a2﹣a2 C.a2﹣a2 D.πa2﹣a2
【解答】解:由图象可以看出,
4个相同阴影部分的面积=四个半圆的面积﹣正方形的面积=﹣a2,
∴题中阴影部分面积为,
故选:A.
8.(3分)小华想用一个圆心角为120°,半径为6cm的扇形做一个圆锥的侧面(接缝忽略不计),则做成的圆锥底面半径为( )
A.4cm B.3cm C.2cm D.1cm
【解答】解:设底面半径为Rcm,则底面周长=2Rπcm,侧面面积=×2Rπ×6=,∴R=2cm.
故选:C.
9.(3分)如图,A,B是⊙O上的两点,AC是⊙O的切线,∠B=70°,则∠BAC等于( )
A.70° B.35° C.20° D.10°
【解答】解:∵OA=OB,
∴∠B=∠OAB=70°,
∵AC是⊙O的切线,
∴OA⊥AC,
则∠BAC=20°.
故选:C.
10.(3分)如图,PA、PB是⊙O的切线,切点分别为A、B,点C在⊙O上,如果∠P=50°,那么∠ACB等于( )
A.40° B.50° C.65° D.130°
【解答】解:连接OA,OB.
根据切线的性质,得∠OBP=∠OAP=90°,
根据四边形的内角和定理得∠AOB=130°,
再根据圆周角定理得∠C=∠AOB=65°.
故选:C.
11.(3分)下列命题中,为真命题的是( )
A.长度相等的弧所对的圆心角相等
B.垂直于圆的半径的直线是该圆的切线
C.过弦的中点的直线必过圆心
D.三角形的外心到三个顶点的距离相等
【解答】解:A、长度相等的弧不一定是等弧,错误;
B、应经过半径的外端.错误;
C、垂径定理及其推论是知二推三,少一个条件,错误;
D、正确.
故选:D.
12.(3分)已知P为边长是2的正六边形ABCDEF内一点,P点到各边的距离分别为h1、h2、h3 h4、h5、h6,则h1+h2+h3+h4+h5+h6=( )
A.2 B.4 C.6 D.8
【解答】解:如图所示,
∵P为边长是2的正六边形ABCDEF内一点,P点到各边的距离分别为h1、h2、h3 h4、h5、h6,
∴S正六边形ABCDEF=×2(h1+h2+h3+h4+h5+h6),
过正六边形的中心O作OG⊥BC于点G,则S正六边形ABCDEF=6××2OG=6OG,
∴h1+h2+h3+h4+h5+h6=6OG,
∵∠OBC=60°,OG⊥BC,
∴BG=BC=2,OG=BG tan60°=1×=,
∴h1+h2+h3+h4+h5+h6=6OG=6×=6.
故选:C.
二、填空题:(本大题有6小题,每小题4分,满分24分)
13.(4分)两圆的半径比是5:3,外切时圆心距是32cm,当两圆内切时,圆心距为 8 cm.
【解答】解:设大圆的半径为R,小圆的半径为r,则有
R:r=5:3;
又因为R+r=32,
解得R=20,r=12,
故当它们内切时,圆心距=20﹣12=8(cm).
故答案为:8.
14.(4分)如图,一扇形纸扇完全打开后,外侧两竹条AB和AC的夹角为120°,AB长为30cm,贴纸部分的宽为20cm,则贴纸部分的面积为 cm2.
【解答】解:S=﹣=cm2.
15.(4分)半径分别为4和5的相交两圆所成的公共弦长为6,则两圆的圆心距为 4+或4﹣ .
【解答】解:根据相交两圆的连心线垂直平分两圆的公共弦,得弦的一半是3,
分别运用勾股定理计算,
连心线和弦的交点到两个圆心的距离是和4,
如果公共弦在两个圆心之间,则圆心距是4+,
如果公共弦在两圆圆心的外部,则圆心距是4﹣.
16.(4分)在半径为5cm的⊙O中,如果弦CD=8cm,直径AB⊥CD,垂足为E,则AE的长为 2或8 cm.
【解答】解:(1)因为直径AB⊥CD,所以CE=ED=8×=4cm,
因为半径为5cm,所以在直角三角形中,
OE===3cm,
AE=5+3=8cm;
(2)将A、B改变位置,即可得到AE=5﹣3=2cm.
因此,AE的长为2cm或8cm.
17.(4分)如图,已知AB是⊙O的弦,P是AB上一点,若AB=10cm,PB=4cm,OP=5cm,则⊙O的半径等于 7 cm.
【解答】解:将OP向两方延长,
设OC=xcm,则CP=(x+5)cm,PD=(x﹣5)cm,
根据相交弦定理,AP BP=CP DP,即(10﹣4)×4=(x+5)(x﹣5),
解得x2=49,x=7或x=﹣7(负值舍去),
则⊙O的半径等于7cm.
18.(4分)如图,A,B,C是⊙O上三点,当BC平分∠ABO时,能得出结论: AB∥OC (任写一个).
【解答】解:∵A,B,C是⊙O上三点,当BC平分∠ABO时,
∴∠CBO=∠CBA.
∵OB=OC,
∴∠OCB=∠OBC.
∴∠CBA=∠OCB.
∴AB∥OC.
三、解答题
19.(5分)附加题:如图是某工件的二视图,按图中尺寸求工件的表面积.
【解答】解:由二视图得:圆柱的底面半径为r=1cm,圆柱的高为h1=1cm,
圆锥的底面半径r=1cm,圆锥高,则圆柱的侧面积S圆柱侧=2πrh1=2π(cm2),
圆柱的底面积S=πr2=π(cm2),
又圆锥的母线,∴圆锥的侧面积S圆锥侧=πrl=2π(cm2).
∴此工件的表面积为S表=S圆柱侧+S圆锥侧+S=5π(cm2).
20.(6分)已知:⊙O1与⊙O2外切于P,AC是过P点的割线,交⊙O1于A,交⊙O2于C,BC切⊙O2于C,过点O1作直线AB交BC于B.求证:AB⊥BC.
【解答】解:连接O1O2,O2C,
∵BC切⊙O2于C,
∴O2C⊥BC,
∵O1O2连接线经过P,
∴AO1=O1P,O2P=O2C,
又∵∠O1PA=∠O2PC,
∴∠PAO1=∠O1PA=∠O2PC=∠O2CP,
∴AB∥O2C,
∴AB⊥BC.
21.(6分)如图,P是⊙O的弦CB延长线上一点,点A在⊙O上,且∠PCA=∠BAP.
求证:PA是⊙O的切线.
【解答】证明:作⊙O的直径AD,连接BD.
则∠C=∠D(同弧所对的圆周角相等),∠ABD=90°(直径所对的圆周角是直角),
∴∠D+∠BAD=90°,
∴∠C+∠BAD=90°(等量代换);
又∵∠PCA=∠BAP,
∴∠BAD+∠PAB=90°,即AP⊥AD,
∴PA是⊙O的切线.
22.(7分)如图,∠PAQ是直角,⊙O与AP相切于点T,与AQ交于B、C两点.
(1)BT是否平分∠OBA,说明你的理由;
(2)若已知AT=4,弦BC=6,试求⊙O的半径R.
【解答】(1)BT平分∠OBA,理由为:
证明:连接OT,如图所示,
∵AP与圆O相切,
∴OT⊥AP,
∴∠OTP=90°,
又∠QAP=90°,
∴∠OTP=∠QAP,
∴OT∥QA,
∴∠OTB=∠ABT,
又∵OB=OT,
∴∠OBT=∠OTB,
∴∠OBT=∠ABT,
则BT平分∠OBA;
(2)解:过O作OD⊥BC,又BC=6,
可得D为BC的中点,即BD=CD=3,
∵四边形ODAT为矩形,
∴OD=AT=4,
在Rt△OBD中,BD=3,OD=4,
根据勾股定理得:OB==5,
则圆的半径为5.
23.(7分)如图,一块直角三角板形状的木板余料,木工师傅要在此余料上锯出一块圆形的木板制作凳面,要想使锯出的凳面的面积最大
(1)请你试着用直尺和圆规画出此圆(要求尺规作图,保留作图痕迹,不写作法).
(2)若此Rt△ABC的直角边分别为30cm和40cm,试求此圆凳面的面积.
【解答】解:(1)如图所示:
(2)设三角形内切圆半径为r,则
r (50+40+30)=×30×40,
解得:r=10(cm).
故此圆凳面的面积为:π×102=100π(cm 2).
24.(6分)如图,已知⊙O的半径为R,直径AB⊥CD以B为圆心,以BC为半径作弧CED.求弧CED与弧CAD围成的新月形ACED的面积S.
【解答】解:∵CD⊥BA,OC=OD=OB,
∴△BCD是等腰直角三角形,CB⊥BD,BC=R.
∴S阴影=S半圆CDA﹣S扇形BCD+S△BCD=πR2﹣π (R)2+×(R)2=R2.
25.(7分)如图,在一个横截面为Rt△ABC的物体中,∠CAB=30°,BC=1米.工人师傅把此物体搬到墙边,先将AB边放在地面(直线l)上,再按顺时针方向绕点B翻转到△A1B1C1的位置(BC1在l上),最后沿BC1的方向移到△A2B2C2的位置,其平移的距离为线段AC的长度(此时A2C2恰好靠在墙边).
(1)请直接写出AB、AC的长;
(2)画出在搬动此物的整个过程A点所经过的路径,并求出该路径的长度(精确到0.1米).
【解答】解:(1)∵∠CAB=30°,BC=1米
∴AB=2米,AC=米(4分).
(2)画出A点经过的路径:(5分)
∵∠ABA1=180°﹣60°=120°,A1A2=AC=米
∴A点所经过的路径长=+(7分)
=π+≈5.9(米)(8分).
26.(6分)如图,AB为⊙O直径,自圆上一点P作AB的垂线PH,垂足为H,自点A向过P点的切线作垂线,垂足为K.求证:AH=AK.
【解答】证明:连接OP,过点O作OC⊥AK于点C,
∴∠OCK=90°,
∵PK是⊙O的切线,AK⊥PK,
∴∠OPK=∠PKC=90°,
∴四边形OCKP是矩形,
∴OP=CK,AK∥OP,
∴∠A=∠POH,
在△AOC和△OPH中,
,
∴△AOC≌△OPH(AAS),
∴AC=OH,
∵AK=AC+CK,AH=OA+OH=OP+OH,
∴AH=AK.
27.(10分)已知:如图,AB是⊙O的一条弦,点C为的中点,CD是⊙O的直径,过C点的直线l交AB所在直线于点E,交⊙O于点F.
(1)判定图中∠CEB与∠FDC的数量关系,并写出结论;
(2)将直线l绕C点旋转(与CD不重合),在旋转过程中,E点,F点的位置也随之变化,请你在下面两个备用图中分别画出在不同位置时,使(1)的结论仍然成立的图形,标上相应字母,选其中一个图形给予证明.
【解答】(1)解:∠CEB=∠FDC;
理由:∵CD是⊙O的直径,点C为的中点,
∴CD⊥AB,
∴∠CEB+∠ECD=90°,
∵CD是⊙O的直径,
∴∠CFD=90°.
∴∠FDC+∠ECD=90°.
∴∠CEB=∠FDC.
(2)证明:如图②
∵CD是⊙O的直径,点C为的中点,
∴CD⊥AB,
∴∠CEB+∠ECD=90°,
∵CD是⊙O的直径,
∴∠CFD=90°.
∴∠FDC+∠ECD=90°.
∴∠CEB=∠FDC.
443576
13
第1页(共1页)
同课章节目录
