北师大版数学八年级上册 3.3轴对称和坐标变化课件(共31张PPT)
文档属性
| 名称 | 北师大版数学八年级上册 3.3轴对称和坐标变化课件(共31张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-08 12:40:56 | ||
图片预览








文档简介
(共31张PPT)
轴对称与坐标变化
学习目标(1分钟)
1、掌握轴对称变换的技巧与规律
2、掌握图形坐标的变化与图形轴对称变换
之间的关系
自学指导(2分钟)
学生自学,老师巡视(6)
阅读课本P68~P69的内容:
1、观察图3-18中的两面小旗,回答(1)(2)
中的问题。
2、根据例一思考:
图形上的所有点的横坐标不变,纵坐标分别乘以
-1,所得图形和原来的图形关于_____对称;
若纵坐标不变,横坐标分别乘以-1,所得新图形
与 原图形关于______对称;
若横、纵坐标均乘以-1,所得新图形与原图形关
于________对称.
3、参考P69议一议,思考:坐标具有这样的关系的点
关于坐标轴对称吗?
X 轴
y 轴
原点
自学检测(12分钟)
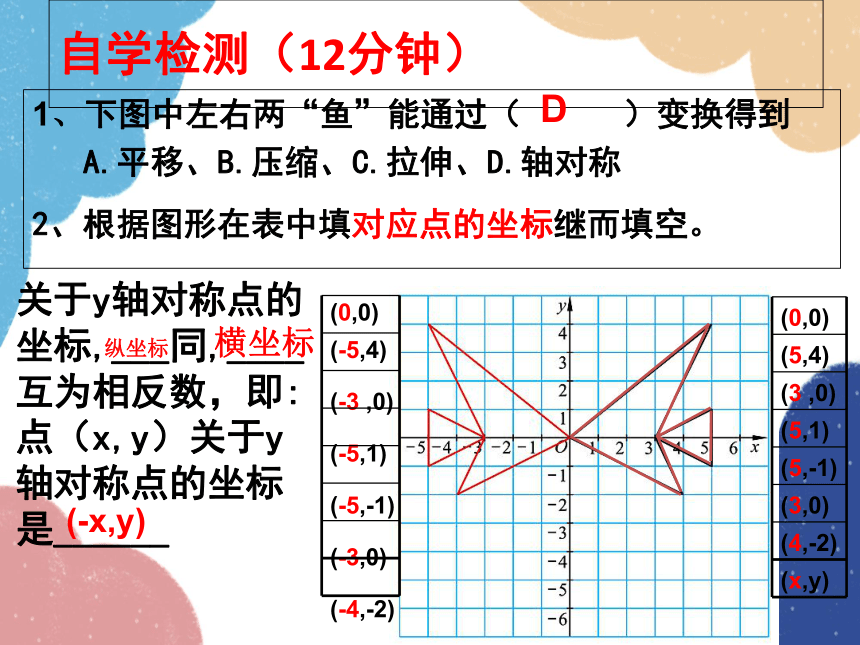
1、下图中左右两“鱼”能通过( )变换得到
A.平移、B.压缩、C.拉伸、D.轴对称
(0,0)
(-5,4)
(-3 ,0)
(-5,1)
(-5,-1)
(-3,0)
(-4,-2)
(-x,y)
(0,0)
(5,4)
(3 ,0)
(5,1)
(5,-1)
(3,0)
(4,-2)
(x,y)
D
关于y轴对称点的坐标,___同,____ 互为相反数,即: 点(x,y)关于y轴对称点的坐标是______
(-x,y)
纵坐标
横坐标
2、根据图形在表中填对应点的坐标继而填空。
-5 -4 -3 -2 -1 0 1 2 3 4 5 x
1
-1
5
4
3
2
-2
-5
-4
-3
y
(x,-y)
(x,y)
(0,0)
(5,4)
(3 ,0)
(5,1)
(5,-1)
(3,0)
(4,-2)
(0,0)
(5,-4)
(3 ,-0)
(5, -1)
(5,1)
(3,0)
(4,2)
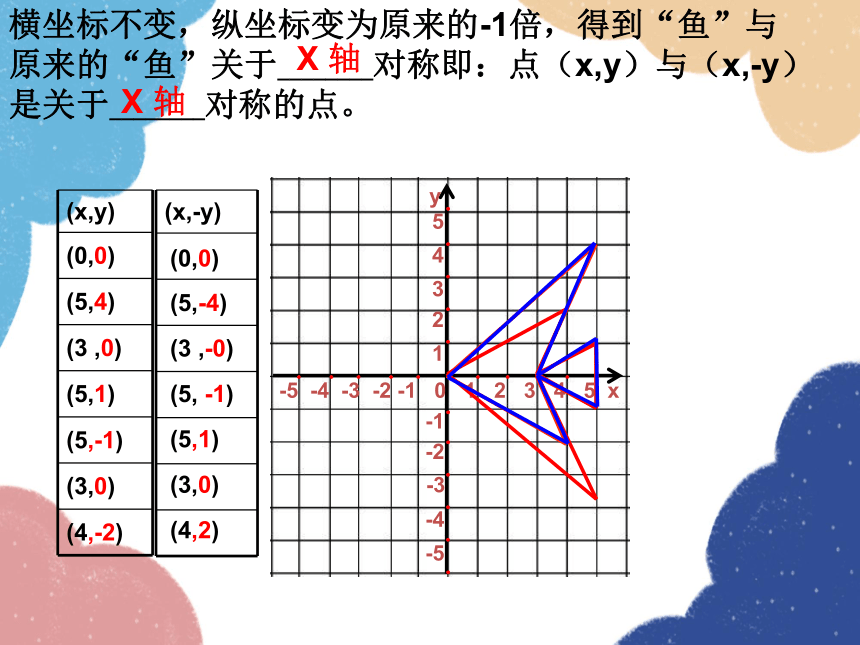
横坐标不变,纵坐标变为原来的-1倍,得到“鱼”与
原来的“鱼”关于________对称即:点(x,y)与(x,-y)是关于________对称的点。
X 轴
X 轴
-5 -4 -3 -2 -1 0 1 2 3 4 5 x
1
-1
5
4
3
2
-2
-5
-4
-3
y
(-x,-y)
(x,y)
(0,0)
(5,4)
(3 ,0)
(5,1)
(5,-1)
(3,0)
(4,-2)
(0,0)
(-5,-4)
(-3 ,0)
(-5, -1)
(-5,1)
(-3,0)
(-4,2)
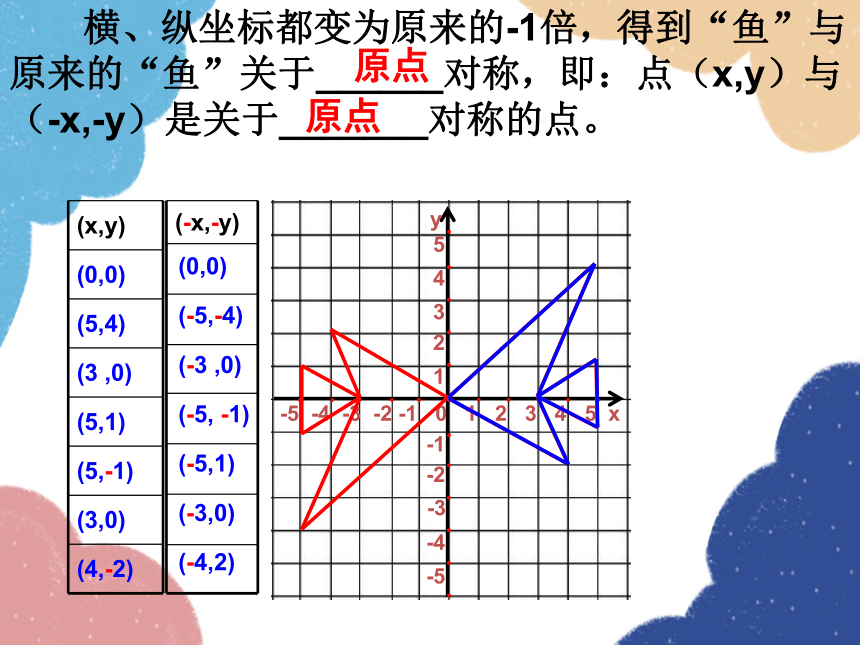
横、纵坐标都变为原来的-1倍,得到“鱼”与原来的“鱼”关于______对称,即:点(x,y)与(-x,-y)是关于_______对称的点。
原点
原点
-5 -4 -3 -2 - 1 0 1 2 3 4 5 x
1
-1
5
4
3
2
-2
-5
-4
-3
y
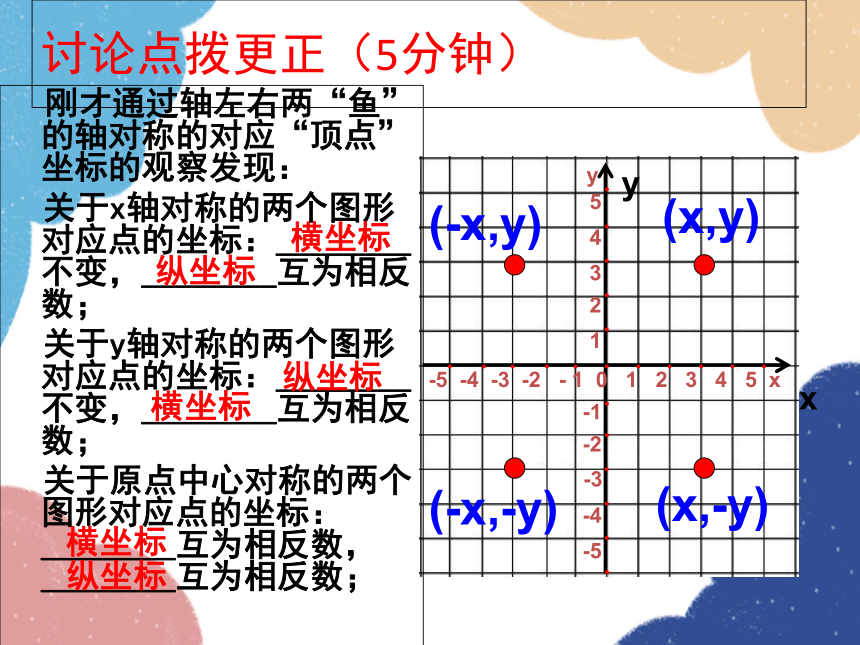
讨论点拨更正(5分钟)
刚才通过轴左右两“鱼”的轴对称的对应“顶点”坐标的观察发现:
关于x轴对称的两个图形对应点的坐标:________不变,________互为相反数;
关于y轴对称的两个图形对应点的坐标:________不变,________互为相反数;
关于原点中心对称的两个图形对应点的坐标:________互为相反数,________互为相反数;
横坐标
纵坐标
纵坐标
横坐标
横坐标
纵坐标
(-x,y)
(x,y)
(x,-y)
(-x,-y)
x
y
1.已知在第二象限的点M到x轴的距离为2,到y轴的距离为3,则M点关于原点对称点的坐标为( )
A.(3,-2)B.(-3,-2)C.(2,3)D.(-3,2)
当堂训练(18分钟)
2.点P(-2,5)关于原点的对称点的坐标_______.
3.把点A(4,-5 )的横坐标不变,纵坐标乘以 -1得到的点的坐标为________,这个点和点A关于______对称
(2,-5)
(4,5)
X轴
4.点A(a, 3)和点B(2,b)关于y轴对称,则 a+b= 。
1
A
5. 完成P69习题3、5 1(做在书上)
6.点A(4,-3)关于x轴的对称点是点B,则线段AB的长是__________个单位,点A(4,-3)关于原点的对称点是点C,则线段AC的长是________个单位。
7.如右图,将梯形绕点O旋转180度,请写出所得图案各点的坐标。
6
10
- -
- -
-
8己知两点A(0,4),B(8,2),点P是轴上的一点,求PA+PB的最小值。
A
B
B’
P
10
9.(选做)如图,在直角坐标系中,第一次将△OAB变换成△OA1B1 ,第二次将△OA1B1变换成△OA2B2 ,第三次将△OA2B2变换成△OA3B3 。已知:A(1,3),A1 (2,3),A2 (4,3),A3 (8,3),B(2,0),B1 (4,0), B2 (8,0),B3(16,0)。
(1)观察每次变换前后
的三角形有何变化,找出
规律,按此变换规律再将
△ OA3B3变换成△OA4B4 ,
那么A4的坐标是_______,
B4的坐标是________。
(2)若按第(1)题找到的规律,将△OAB进行n次变换,得到△OAnBn,比较每次变换中三角形顶点有何变化,找出规律,
推测An 的坐标是_________,Bn的坐标是____________。
( 8, 3 )
( 32, 0 )
x
y
A
A1
A2
A3
1
2
3
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
B
B1
B2
B3
^
y
>
x
0
1
1
2
3
4
3
2
-1
-2
-3
-1
-2
-3
-4
如图,三架飞机P、Q、R保持编队飞行,分别写出它们的坐标。 30秒后,飞机P飞到Pˋˊ位置,飞机Q、R飞到了什么位置?你能写出这三架飞机新位置的坐标吗
1.知识目标
(1)认识图形的轴对称、中心对称变换与坐标变化之间的关系.
(2)以平面直角坐标系为工具体会数形结合.
2.教学重点
点的坐标变化与图形变化之间的关系.
3.教学难点
点坐标变化与图形变化之间的变化规律.
在如图所示的平面直
角坐标系中,第一、
二象限内各有一面小
旗.
(1)两面小旗之间有
怎样的位置关系?对
应点A与A1的坐标又
有什么特点?其它对
应的点也有这个特点
吗?
归纳 概括
1.关于x轴对称的两点,它们的横坐标 ,
纵坐标 ;
2.关于y轴对称的两点,它们的横坐标 ,
纵坐标 .
相同
互为相反数
相同
互为相反数
1
2
3
4
5
6
7
8
O
–1
–2
–3
–4
–5
1
2
3
4
9
5
在直角坐标系中描出以下各点:(0,0) (5,4) (3,0) (5,1) (5,-1) (3,0) (4,-2) (0,0)并用线段依次连接,看一看是什么图案.
y
x
1
2
3
4
5
6
7
8
0
–1
–2
–3
–4
–5
1
2
3
4
9
5
将所得图案的各个顶点的纵坐标保持不变,横坐标分别乘-1,依次连接这些点,你会得到怎样的图案?
这个图案与原图案又有着怎样的位置关系呢?
y
x
1
2
3
4
5
-1
-2
-3
0
–1
–2
–3
–4
–5
1
2
3
4
-4
-5
5
y
x
两个图形关于y轴对称
顶点坐标变化:
纵坐标保持不变,
横坐标都乘以-1
(为原横坐标的相
反数).
归纳:纵坐标相同,
横坐标互为相反数
的两点关于y轴对称.
1
2
3
4
5
6
7
8
0
–1
–2
–3
–4
–5
1
2
3
4
5
将各坐标的纵
坐标都乘以
-1,横坐标保
持不变,则图形
怎么变化?
y
x
与原图形关于x轴对称
1
2
3
4
5
6
7
8
0
–1
–2
–3
–4
–5
1
2
3
4
5
将各坐标的纵
坐标都乘以-1,
横坐标保持不
变,则图形怎么
变化?
y
x
与原图形关于x轴对称
归纳:横坐标相同,
纵坐标互为相反
数的两点关于x
轴对称.
–5
将各坐标的纵坐标与横坐标都乘以-1,图形会变成什么样?
y
x
2
3
4
5
1
0
–1
–2
–3
–4
1
2
3
4
5
–1
–2
–3
–4
–5
与原图形关于原点中心对称
归纳:
横,纵坐标都互
为相反数的两
点关于原点对称.
例 已知△ABC 的三个顶点的坐标分别为A(-3,5),B(- 4,1),C (-1,3),作出△ABC 关于y 轴和x 轴对称的图形.
·
·
·
·
A
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
·
·
c
B
B ′
A ′
C ′
1.将平面直角坐标系内某个图形各个点的横坐标不变,纵坐标都乘以-1,所得图形与原图形( )
A. 关于X轴对称. B. 关于Y轴对称
C. 关于原点对称 D. 无法确定
2.点A(-3,2)与点B(-3,-2)的关系是( )
A.关于X轴对称 B.关于Y轴对称
C.关于原点对称 D.以上各项都不对
3.已知点M(3,-2),点N(a,b)是M点关于Y轴的对称点,则 a= , b= .
4.已知点P(a-1,5)和点Q(2,b-1)关于X轴对称,则
a= ,b= .
A
-3
-2
3
-4
跟踪练习
A
A`(-4,-1)
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
C(-3,2)
B(-1,-1)
A(-4,1)
·
·
·
如图,利用关于坐标轴对称的点的坐标的特点,分别作出△ABC关于x轴和y 轴对称的图形.
B``(1,-1)
C``(3,2)
A``(4,1)
·
·
·
·
·
·
C`(-3,-2)
B`(-1,1)
拔尖自助餐
x
y
课堂检测
1.已知点P(2a-3,4),点A(-1,2b+2),
(1)如果点P与点A关于x轴对称,那么a+b=___
(2)如果点P与点A关于y轴对称,那么a+b=___
2.已知A、B两点的坐标分别是(-2,3)和(2,3), 则下面四个结论:①A、B关于x轴对称;②A、B关于y轴对称;③A、B关于原点对称;④A、B之间的距离为4,其中正确的有( ) A.1个 B.2个 C.3个 D.4个
-2
3
B
3.点(m,-1)和点(2,n)关于x轴对称,则mn等于( )
A.- 2 B.2 C.1 D.- 1
4.若点A(1-a,5),B(3 ,b)关于y轴对称,求(2a,-b)的坐标,指出它在第几象限?
B
(8,-5)第四象限
5.已知点P (2a+b,-3a)与点 P′ (8,b+2).
若点p与点p′关于x轴对称,求a、 b的值.
若点p与点p′关于y轴对称,求a、 b的值.
{
2a+b=8
3a=b+2
{
b=4
a=2
{
2a+b=-8
-3a=b+2
{
b=-20
a=6
本节课你学到了什么
感悟与反思
横坐标保持不变,纵坐标分别变为原来的-1倍 新图案与原图案关于x轴对称
纵坐标保持不变,横坐标分别变为原来的-1倍 新图案与原图案关于y轴对称
横坐标和纵坐标分别变为原来的-1倍 新图案与原图案关于原点中心对称
小 结
祝同学们学习进步!
再见!
轴对称与坐标变化
学习目标(1分钟)
1、掌握轴对称变换的技巧与规律
2、掌握图形坐标的变化与图形轴对称变换
之间的关系
自学指导(2分钟)
学生自学,老师巡视(6)
阅读课本P68~P69的内容:
1、观察图3-18中的两面小旗,回答(1)(2)
中的问题。
2、根据例一思考:
图形上的所有点的横坐标不变,纵坐标分别乘以
-1,所得图形和原来的图形关于_____对称;
若纵坐标不变,横坐标分别乘以-1,所得新图形
与 原图形关于______对称;
若横、纵坐标均乘以-1,所得新图形与原图形关
于________对称.
3、参考P69议一议,思考:坐标具有这样的关系的点
关于坐标轴对称吗?
X 轴
y 轴
原点
自学检测(12分钟)
1、下图中左右两“鱼”能通过( )变换得到
A.平移、B.压缩、C.拉伸、D.轴对称
(0,0)
(-5,4)
(-3 ,0)
(-5,1)
(-5,-1)
(-3,0)
(-4,-2)
(-x,y)
(0,0)
(5,4)
(3 ,0)
(5,1)
(5,-1)
(3,0)
(4,-2)
(x,y)
D
关于y轴对称点的坐标,___同,____ 互为相反数,即: 点(x,y)关于y轴对称点的坐标是______
(-x,y)
纵坐标
横坐标
2、根据图形在表中填对应点的坐标继而填空。
-5 -4 -3 -2 -1 0 1 2 3 4 5 x
1
-1
5
4
3
2
-2
-5
-4
-3
y
(x,-y)
(x,y)
(0,0)
(5,4)
(3 ,0)
(5,1)
(5,-1)
(3,0)
(4,-2)
(0,0)
(5,-4)
(3 ,-0)
(5, -1)
(5,1)
(3,0)
(4,2)
横坐标不变,纵坐标变为原来的-1倍,得到“鱼”与
原来的“鱼”关于________对称即:点(x,y)与(x,-y)是关于________对称的点。
X 轴
X 轴
-5 -4 -3 -2 -1 0 1 2 3 4 5 x
1
-1
5
4
3
2
-2
-5
-4
-3
y
(-x,-y)
(x,y)
(0,0)
(5,4)
(3 ,0)
(5,1)
(5,-1)
(3,0)
(4,-2)
(0,0)
(-5,-4)
(-3 ,0)
(-5, -1)
(-5,1)
(-3,0)
(-4,2)
横、纵坐标都变为原来的-1倍,得到“鱼”与原来的“鱼”关于______对称,即:点(x,y)与(-x,-y)是关于_______对称的点。
原点
原点
-5 -4 -3 -2 - 1 0 1 2 3 4 5 x
1
-1
5
4
3
2
-2
-5
-4
-3
y
讨论点拨更正(5分钟)
刚才通过轴左右两“鱼”的轴对称的对应“顶点”坐标的观察发现:
关于x轴对称的两个图形对应点的坐标:________不变,________互为相反数;
关于y轴对称的两个图形对应点的坐标:________不变,________互为相反数;
关于原点中心对称的两个图形对应点的坐标:________互为相反数,________互为相反数;
横坐标
纵坐标
纵坐标
横坐标
横坐标
纵坐标
(-x,y)
(x,y)
(x,-y)
(-x,-y)
x
y
1.已知在第二象限的点M到x轴的距离为2,到y轴的距离为3,则M点关于原点对称点的坐标为( )
A.(3,-2)B.(-3,-2)C.(2,3)D.(-3,2)
当堂训练(18分钟)
2.点P(-2,5)关于原点的对称点的坐标_______.
3.把点A(4,-5 )的横坐标不变,纵坐标乘以 -1得到的点的坐标为________,这个点和点A关于______对称
(2,-5)
(4,5)
X轴
4.点A(a, 3)和点B(2,b)关于y轴对称,则 a+b= 。
1
A
5. 完成P69习题3、5 1(做在书上)
6.点A(4,-3)关于x轴的对称点是点B,则线段AB的长是__________个单位,点A(4,-3)关于原点的对称点是点C,则线段AC的长是________个单位。
7.如右图,将梯形绕点O旋转180度,请写出所得图案各点的坐标。
6
10
- -
- -
-
8己知两点A(0,4),B(8,2),点P是轴上的一点,求PA+PB的最小值。
A
B
B’
P
10
9.(选做)如图,在直角坐标系中,第一次将△OAB变换成△OA1B1 ,第二次将△OA1B1变换成△OA2B2 ,第三次将△OA2B2变换成△OA3B3 。已知:A(1,3),A1 (2,3),A2 (4,3),A3 (8,3),B(2,0),B1 (4,0), B2 (8,0),B3(16,0)。
(1)观察每次变换前后
的三角形有何变化,找出
规律,按此变换规律再将
△ OA3B3变换成△OA4B4 ,
那么A4的坐标是_______,
B4的坐标是________。
(2)若按第(1)题找到的规律,将△OAB进行n次变换,得到△OAnBn,比较每次变换中三角形顶点有何变化,找出规律,
推测An 的坐标是_________,Bn的坐标是____________。
( 8, 3 )
( 32, 0 )
x
y
A
A1
A2
A3
1
2
3
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
B
B1
B2
B3
^
y
>
x
0
1
1
2
3
4
3
2
-1
-2
-3
-1
-2
-3
-4
如图,三架飞机P、Q、R保持编队飞行,分别写出它们的坐标。 30秒后,飞机P飞到Pˋˊ位置,飞机Q、R飞到了什么位置?你能写出这三架飞机新位置的坐标吗
1.知识目标
(1)认识图形的轴对称、中心对称变换与坐标变化之间的关系.
(2)以平面直角坐标系为工具体会数形结合.
2.教学重点
点的坐标变化与图形变化之间的关系.
3.教学难点
点坐标变化与图形变化之间的变化规律.
在如图所示的平面直
角坐标系中,第一、
二象限内各有一面小
旗.
(1)两面小旗之间有
怎样的位置关系?对
应点A与A1的坐标又
有什么特点?其它对
应的点也有这个特点
吗?
归纳 概括
1.关于x轴对称的两点,它们的横坐标 ,
纵坐标 ;
2.关于y轴对称的两点,它们的横坐标 ,
纵坐标 .
相同
互为相反数
相同
互为相反数
1
2
3
4
5
6
7
8
O
–1
–2
–3
–4
–5
1
2
3
4
9
5
在直角坐标系中描出以下各点:(0,0) (5,4) (3,0) (5,1) (5,-1) (3,0) (4,-2) (0,0)并用线段依次连接,看一看是什么图案.
y
x
1
2
3
4
5
6
7
8
0
–1
–2
–3
–4
–5
1
2
3
4
9
5
将所得图案的各个顶点的纵坐标保持不变,横坐标分别乘-1,依次连接这些点,你会得到怎样的图案?
这个图案与原图案又有着怎样的位置关系呢?
y
x
1
2
3
4
5
-1
-2
-3
0
–1
–2
–3
–4
–5
1
2
3
4
-4
-5
5
y
x
两个图形关于y轴对称
顶点坐标变化:
纵坐标保持不变,
横坐标都乘以-1
(为原横坐标的相
反数).
归纳:纵坐标相同,
横坐标互为相反数
的两点关于y轴对称.
1
2
3
4
5
6
7
8
0
–1
–2
–3
–4
–5
1
2
3
4
5
将各坐标的纵
坐标都乘以
-1,横坐标保
持不变,则图形
怎么变化?
y
x
与原图形关于x轴对称
1
2
3
4
5
6
7
8
0
–1
–2
–3
–4
–5
1
2
3
4
5
将各坐标的纵
坐标都乘以-1,
横坐标保持不
变,则图形怎么
变化?
y
x
与原图形关于x轴对称
归纳:横坐标相同,
纵坐标互为相反
数的两点关于x
轴对称.
–5
将各坐标的纵坐标与横坐标都乘以-1,图形会变成什么样?
y
x
2
3
4
5
1
0
–1
–2
–3
–4
1
2
3
4
5
–1
–2
–3
–4
–5
与原图形关于原点中心对称
归纳:
横,纵坐标都互
为相反数的两
点关于原点对称.
例 已知△ABC 的三个顶点的坐标分别为A(-3,5),B(- 4,1),C (-1,3),作出△ABC 关于y 轴和x 轴对称的图形.
·
·
·
·
A
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
·
·
c
B
B ′
A ′
C ′
1.将平面直角坐标系内某个图形各个点的横坐标不变,纵坐标都乘以-1,所得图形与原图形( )
A. 关于X轴对称. B. 关于Y轴对称
C. 关于原点对称 D. 无法确定
2.点A(-3,2)与点B(-3,-2)的关系是( )
A.关于X轴对称 B.关于Y轴对称
C.关于原点对称 D.以上各项都不对
3.已知点M(3,-2),点N(a,b)是M点关于Y轴的对称点,则 a= , b= .
4.已知点P(a-1,5)和点Q(2,b-1)关于X轴对称,则
a= ,b= .
A
-3
-2
3
-4
跟踪练习
A
A`(-4,-1)
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
C(-3,2)
B(-1,-1)
A(-4,1)
·
·
·
如图,利用关于坐标轴对称的点的坐标的特点,分别作出△ABC关于x轴和y 轴对称的图形.
B``(1,-1)
C``(3,2)
A``(4,1)
·
·
·
·
·
·
C`(-3,-2)
B`(-1,1)
拔尖自助餐
x
y
课堂检测
1.已知点P(2a-3,4),点A(-1,2b+2),
(1)如果点P与点A关于x轴对称,那么a+b=___
(2)如果点P与点A关于y轴对称,那么a+b=___
2.已知A、B两点的坐标分别是(-2,3)和(2,3), 则下面四个结论:①A、B关于x轴对称;②A、B关于y轴对称;③A、B关于原点对称;④A、B之间的距离为4,其中正确的有( ) A.1个 B.2个 C.3个 D.4个
-2
3
B
3.点(m,-1)和点(2,n)关于x轴对称,则mn等于( )
A.- 2 B.2 C.1 D.- 1
4.若点A(1-a,5),B(3 ,b)关于y轴对称,求(2a,-b)的坐标,指出它在第几象限?
B
(8,-5)第四象限
5.已知点P (2a+b,-3a)与点 P′ (8,b+2).
若点p与点p′关于x轴对称,求a、 b的值.
若点p与点p′关于y轴对称,求a、 b的值.
{
2a+b=8
3a=b+2
{
b=4
a=2
{
2a+b=-8
-3a=b+2
{
b=-20
a=6
本节课你学到了什么
感悟与反思
横坐标保持不变,纵坐标分别变为原来的-1倍 新图案与原图案关于x轴对称
纵坐标保持不变,横坐标分别变为原来的-1倍 新图案与原图案关于y轴对称
横坐标和纵坐标分别变为原来的-1倍 新图案与原图案关于原点中心对称
小 结
祝同学们学习进步!
再见!
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
