圆周角[上学期]

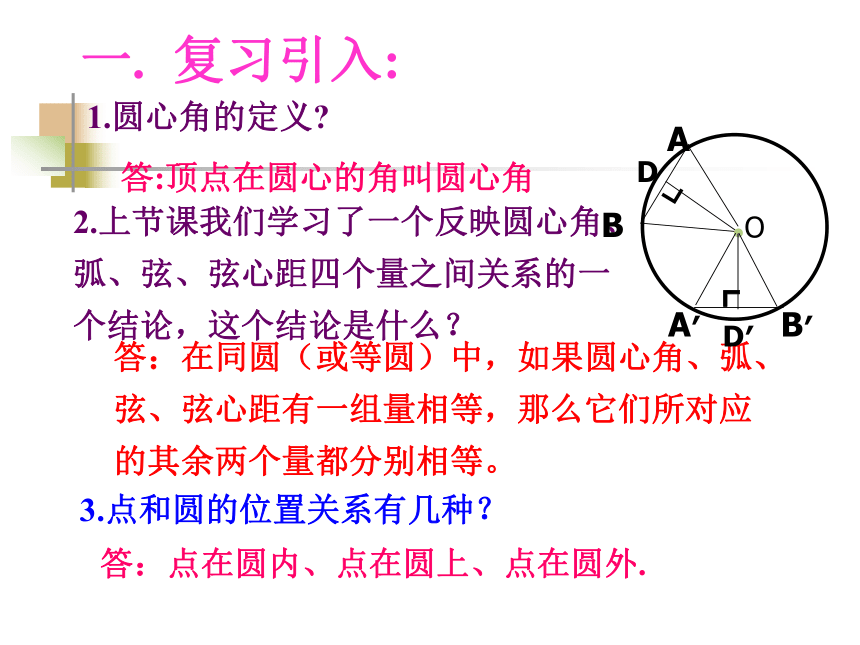
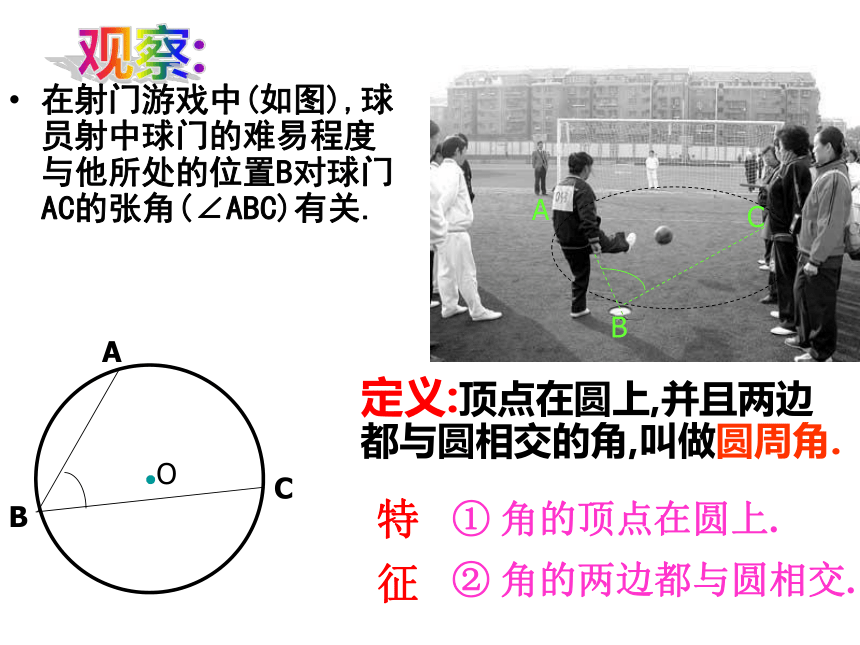
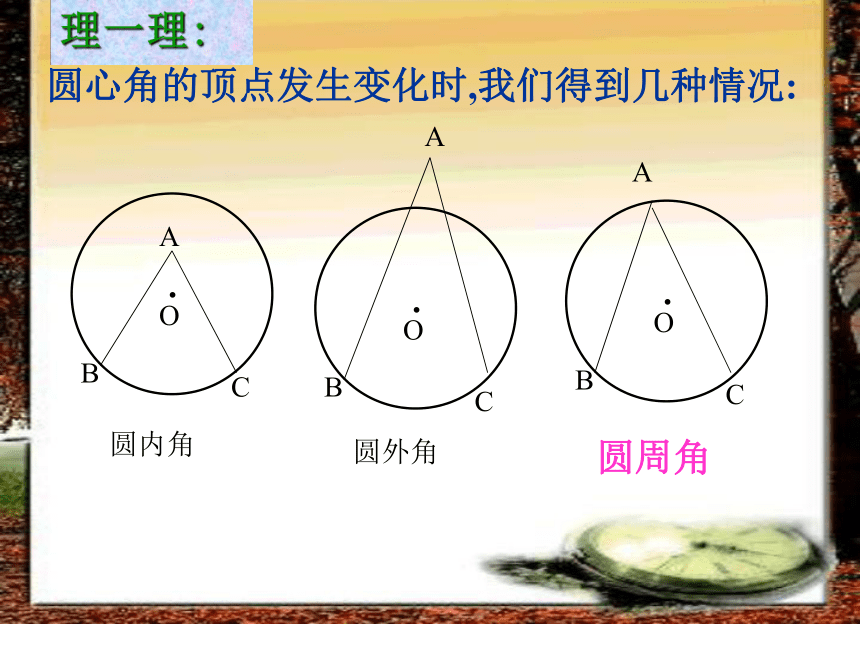
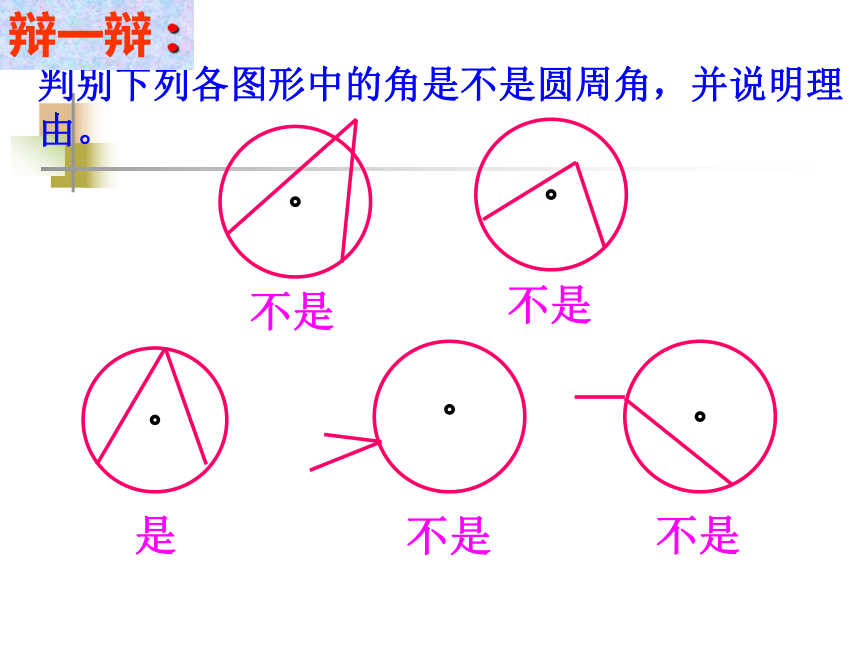
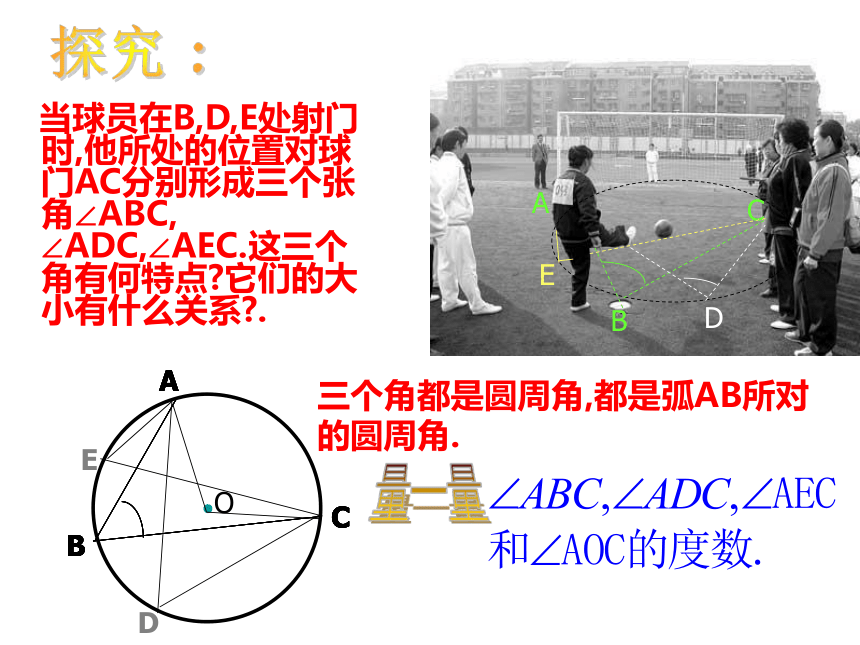
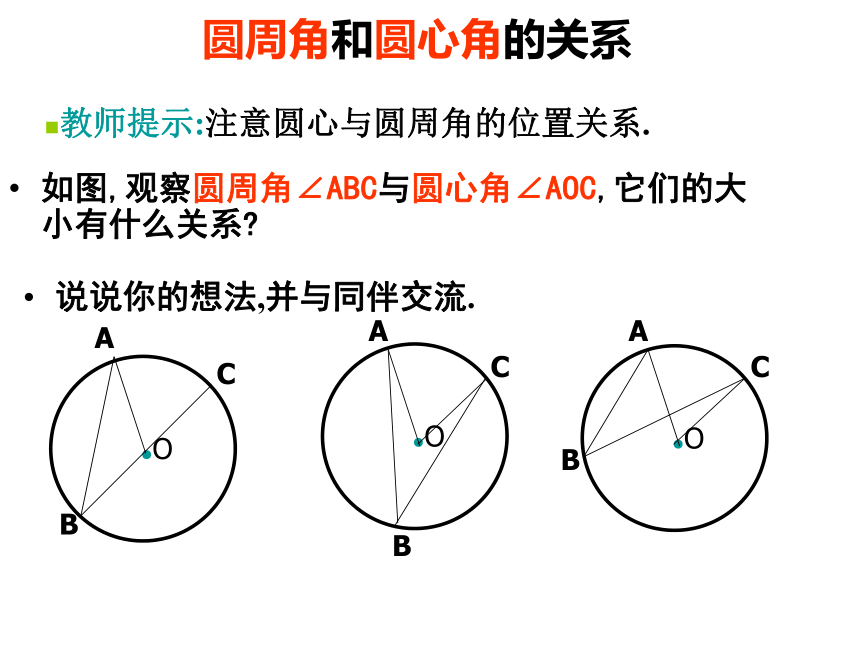
课件22张PPT。ABCO圆周角一. 复习引入:1.圆心角的定义?答：在同圆（或等圆）中，如果圆心角、弧、弦、弦心距有一组量相等，那么它们所对应的其余两个量都分别相等。答:顶点在圆心的角叫圆心角2.上节课我们学习了一个反映圆心角、弧、弦、弦心距四个量之间关系的一个结论，这个结论是什么？3.点和圆的位置关系有几种？答：点在圆内、点在圆上、点在圆外.在射门游戏中(如图),球员射中球门的难易程度与他所处的位置B对球门AC的张角(∠ABC)有关.定义:顶点在圆上,并且两边都与圆相交的角,叫做圆周角.观察:特 征圆心角的顶点发生变化时,我们得到几种情况:A.OBCAA圆内角圆外角圆周角理一理:判别下列各图形中的角是不是圆周角，并说明理由。不是不是是不是不是辩一辩 : 当球员在B,D,E处射门时,他所处的位置对球门AC分别形成三个张角∠ABC, ∠ADC,∠AEC.这三个角有何特点?它们的大小有什么关系?.探究?:量一量三个角都是圆周角,都是弧AB所对的圆周角.类比圆心角探知圆周角在同圆或等圆中,同弧或等弧所对的圆心角相等.在同圆或等圆中,同弧或等弧所对的圆周角有什么关系？ 为了解决这个问题,我们先探究同弧所对的圆周角和圆心角之间有的关系.你会画同弧所对的圆周角和圆心角吗?圆周角和圆心角的关系如图,观察圆周角∠ABC与圆心角∠AOC,它们的大小有什么关系?说说你的想法,并与同伴交流.教师提示:注意圆心与圆周角的位置关系.圆周角和圆心角的关系1.首先考虑一种特殊情况：
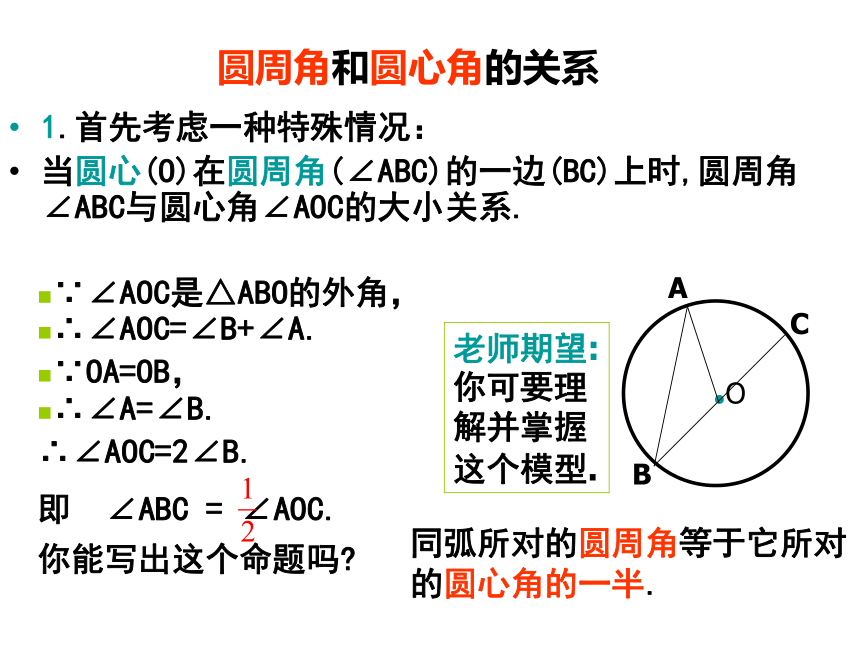
当圆心(O)在圆周角(∠ABC)的一边(BC)上时,圆周角∠ABC与圆心角∠AOC的大小关系.∵∠AOC是△ABO的外角，∴∠AOC=∠B+∠A.∵OA=OB，∴∠A=∠B.∴∠AOC=2∠B.即 ∠ABC = ∠AOC.你能写出这个命题吗?同弧所对的圆周角等于它所对的圆心角的一半.老师期望:你可要理解并掌握这个模型.如果圆心不在圆周角的一边上,结果会怎样?
2.当圆心(O)在圆周角(∠ABC)的内部时,圆周角∠ABC与圆心角∠AOC的大小关系会怎样?老师提示:能否转化为1的情况?过点B作直径BD.由1可得: ∴ ∠ABC = ∠AOC.你能写出这个命题吗?同弧所对的圆周角等于它所对的圆心角的一半.∠ABD = ∠AOD,∠CBD = ∠COD,圆周角和圆心角的关系圆周角和圆心角的关系如果圆心不在圆周角的一边上,结果会怎样?
3.当圆心(O)在圆周角(∠ABC)的外部时,圆周角∠ABC与圆心角∠AOC的大小关系会怎样?老师提示:能否也转化为1的情况?过点B作直径BD.由1可得:∴ ∠ABC = ∠AOC.你能写出这个命题吗?同弧所对的圆周角等于它所对的圆心角的一半.∠ABD = ∠AOD,∠CBD = ∠COD,综上所述,圆周角∠ABC与圆心角∠AOC的大小关系是:同弧所对的圆周角等于它所对的圆心角的一半.即 ∠ABC = ∠AOC.如图所示，∠ADB、∠ACB、∠AOB 分别是什么角？ 它们 有何共同点？ ∠ADB与∠ACB有什么关系？ 同弧 所对的圆周角相等.(等弧)思考:
相等的圆周角所对的弧相等吗?在同圆或等圆中都等于这条弧所对的圆心角的一半.圆周角定理:ABCD在同圆或等圆中相等的圆周角所对的弧相等.则 ∠ D=∠A∴AB∥CD1.如图,在⊙O中,∠BOC=50°,求∠A的大小.解: ∠A = ∠BOC = 25°.如图,AB是直径,则∠ACB=＿＿＿＿90 度半圆（或直径）所对的圆周角是直角，90度的圆周角所对的弦是直径。2.试找出下图中所有相等的圆周角。 ∠2=∠7∠1=∠4∠3=∠6∠5=∠83：已知⊙O中弦AB的等于半径，
求弦AB所对的圆心角和圆周角的度数。 圆心角为60度圆周角为 30 度或 150 度。4.如图，∠A是圆O的圆周角， ∠A=40°，求∠OBC的度数。 例: 如图，AB是⊙O的直径AB=10cm,
弦AC=6cm,∠ACB的平分线交⊙O于点D . 求 BC, AD ,BD 的长.106练习:如图 AB是⊙O的直径, C ,D是圆上的两点,若∠ABD=40°,则∠BCD=＿＿＿＿＿.40°50°五.课堂小结1. 【圆周角的定义】 顶点在圆上，两边都与圆相交，这样的角叫圆周角。 2. 【圆周角的性质】 （3）在同圆（或等圆）中，同弧或等弧所对的圆周角相等，都等于该弧所对的圆心角的一半； 相等的圆周角所对的弧相等；

（2）一条弧所对的圆周角等于该弧所对的圆心角的一半；（1）半圆或直径所对的圆周角都相等，都等于90°（直角）． 90°的圆周角所对的弦是圆的直径 驶向胜利的彼岸六.作业再见！