2.密铺(课件)-五年级上册数学冀教版(共41张PPT)
文档属性
| 名称 | 2.密铺(课件)-五年级上册数学冀教版(共41张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-08 13:00:38 | ||
图片预览







文档简介
(共41张PPT)
密 铺
五年级数学上册
1
先看下面几个密铺的图案
观察下图,这些图形在拼接时有什么特点
用形状、大小完全相同的一种或几种平面图形进行拼接,彼此之间不留空隙、不重叠地铺成一片,这就是平面图形的密铺,又称作平面图形的镶嵌。
平面图形的密铺
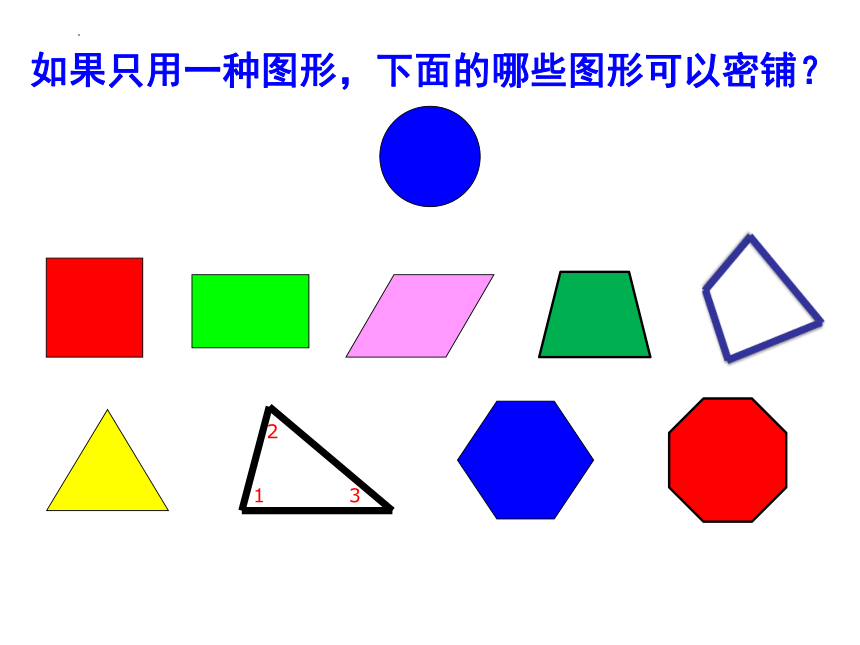
如果只用一种图形,下面的哪些图形可以密铺?
1
3
2
操作要求:
1、小组长布置任务,并记录研究结果。
2、要求小组同学分工合作,把密铺的成果展
示在课桌桌面上。
3、铺到能证明自己的猜想就可以了,不用
铺得太多。
4、把铺的结果小组内交流。
12
结论:圆形不可以单独密铺。
13
结论:正方形可以单独密铺。
14
结论:长方形可以单独密铺。
15
结论:平行四边形可以单独密铺。
16
结论:梯形可以单独密铺。
17
平行四边形,长方形和梯形可以进行密铺,那么任意的四边形可以进行密铺嘛?
形状、大小完全相同的任意四边形可以密铺
1
2
3
4
1
2
3
4
1
2
3
4
1
2
3
4
1
2
3
4
1
2
3
4
1
2
3
4
1
2
3
4
用四边形密铺的图案中,观察每个拼接点处有几个角?
它们与这种四边形的四个内角有什么关系?
1
2
3
4
1
2
3
4
1
2
3
4
1
2
3
4
1
2
3
4
1
2
4
3
1
2
3
4
拼接点处几个角的和是360度,
这个平面图形就能密铺。
1
3
4
2
结论:正三角形可以单独密铺。
21
所有的三角形都能单独密铺吗?
等腰三角形
不等边三角形
22
形状、大小完全相同的三角形可以密铺
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
拼接点处几个角的和是360度,
这个平面图形就能密铺。
在用三角形密铺的图案中,观察每个拼接点处有几个角?
它们与这种三角形的三个内角有什么关系?
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
结论:正六边形可以单独密铺。
25
内角和
(6 - 2)×180°=
720°
每一个内角
720°÷6=120°
结论:正八边形不可以单独密铺。
26
内角和
(8 - 2)×180°=
1080°
每一个内角
1080°÷8=135°
结论:正五边形不可以单独密铺。
27
内角和
(5 - 2)×180°=
540°
540°÷5=108°
每一个内角
生活中的密铺图片
说一说
31
32
埃舍尔
(1898-1972)
荷兰画家埃舍尔被人们称为“艺术怪才”,他的画非常有想象力,也非常有趣,能给人带来一种美妙的艺术享受。
33
埃舍尔作品欣赏
埃舍尔作品欣赏
埃舍尔作品欣赏
埃舍尔作品欣赏
埃舍尔作品欣赏
埃舍尔作品欣赏
埃舍尔作品欣赏
如果你有兴趣,课后自己也可以动手设计,相信你会有更出色的设计。
密 铺
五年级数学上册
1
先看下面几个密铺的图案
观察下图,这些图形在拼接时有什么特点
用形状、大小完全相同的一种或几种平面图形进行拼接,彼此之间不留空隙、不重叠地铺成一片,这就是平面图形的密铺,又称作平面图形的镶嵌。
平面图形的密铺
如果只用一种图形,下面的哪些图形可以密铺?
1
3
2
操作要求:
1、小组长布置任务,并记录研究结果。
2、要求小组同学分工合作,把密铺的成果展
示在课桌桌面上。
3、铺到能证明自己的猜想就可以了,不用
铺得太多。
4、把铺的结果小组内交流。
12
结论:圆形不可以单独密铺。
13
结论:正方形可以单独密铺。
14
结论:长方形可以单独密铺。
15
结论:平行四边形可以单独密铺。
16
结论:梯形可以单独密铺。
17
平行四边形,长方形和梯形可以进行密铺,那么任意的四边形可以进行密铺嘛?
形状、大小完全相同的任意四边形可以密铺
1
2
3
4
1
2
3
4
1
2
3
4
1
2
3
4
1
2
3
4
1
2
3
4
1
2
3
4
1
2
3
4
用四边形密铺的图案中,观察每个拼接点处有几个角?
它们与这种四边形的四个内角有什么关系?
1
2
3
4
1
2
3
4
1
2
3
4
1
2
3
4
1
2
3
4
1
2
4
3
1
2
3
4
拼接点处几个角的和是360度,
这个平面图形就能密铺。
1
3
4
2
结论:正三角形可以单独密铺。
21
所有的三角形都能单独密铺吗?
等腰三角形
不等边三角形
22
形状、大小完全相同的三角形可以密铺
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
拼接点处几个角的和是360度,
这个平面图形就能密铺。
在用三角形密铺的图案中,观察每个拼接点处有几个角?
它们与这种三角形的三个内角有什么关系?
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
结论:正六边形可以单独密铺。
25
内角和
(6 - 2)×180°=
720°
每一个内角
720°÷6=120°
结论:正八边形不可以单独密铺。
26
内角和
(8 - 2)×180°=
1080°
每一个内角
1080°÷8=135°
结论:正五边形不可以单独密铺。
27
内角和
(5 - 2)×180°=
540°
540°÷5=108°
每一个内角
生活中的密铺图片
说一说
31
32
埃舍尔
(1898-1972)
荷兰画家埃舍尔被人们称为“艺术怪才”,他的画非常有想象力,也非常有趣,能给人带来一种美妙的艺术享受。
33
埃舍尔作品欣赏
埃舍尔作品欣赏
埃舍尔作品欣赏
埃舍尔作品欣赏
埃舍尔作品欣赏
埃舍尔作品欣赏
埃舍尔作品欣赏
如果你有兴趣,课后自己也可以动手设计,相信你会有更出色的设计。
