安徽省合肥市第五十中学西校2022—2023学年九年级上学期期中数学模拟测试卷(含答案)
文档属性
| 名称 | 安徽省合肥市第五十中学西校2022—2023学年九年级上学期期中数学模拟测试卷(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 242.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-08 00:00:00 | ||
图片预览


文档简介
合肥市五十中学西校九年级上学期期中数学阶段模拟测试卷
一、选择题(本大题共10小题,每小题4分,满分40分)
1. 将抛物线向左平移4个单位,向上平移1个单位所得新抛物线的表达式为( )
A. y=-2(x-4)2-4 B. y=-2(x+4)2-2 C. y=-2x2+4 D. y=-2x2+4
2. 抛物线的顶点坐标是( )
A. B. C. D.
3. 如图,在中,点P在边上,则在下列四个条件中:;;;, 能满足与相似的条件是( )
A. ①②④ B. ①③④ C. ②③④ D. ①②③
4. 关于x的二次函数,当时,y随x的增大而增大,则实数m的取值范围是( )
A. B. C. D.
5. 对于函数(k<0),下列说法错误的是( )
A. 它的图像分布在二、四象限 B. 它的图像既是轴对称图形又是中心对称图形
C. 当x>0时,y的值随x的增大而增大 D. 当x<0时,y的值随x的增大而减小
6. 如图,AC与BD相交于点E,∠A=∠B,若AE=2,CE=4,DE=3,则BE的长是( )
A 6 B. 4 C. D.
(第3题图) (第6题图) (第9题图) (第10题图)
7. 若点A(-3,y1)、B(-1,y2)、C(3,y3)都在反比例函数(k>0)图象上,则y1、y2、y3的大小关系是( )
A. y1>y2>y 3 B. y3>y1>y2 C. y2>y1>y3 D. y1>y3>y2
8. 在同一平面直角坐标系中,函数y=ax2﹣bx与y=bx+a的图象可能是( )
A. B. C. D.
9. 如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,翻折∠B,使点B落在直角边AC上某一点D处,折痕为EF,点E、F分别在边BC、AB上,若△CDE与△ABC相似,则CE的长为( )
A B. C. 或 D. 或
10. 如图,在△ABC中,∠ACB=90°,AC=4,BC=3,P是AB边上一动点,PD⊥AC于点D,点E在P的右侧,且PE=1,连接CE,P从点A出发,沿AB方向运动,当E到达点B时,P停止运动,在整个运动过程中,阴影部分面积S1+S2的大小变化的情况是( )
A. 一直减小 B. 一直增大 C. 先增大后减小 D. 先减小后增大
二、填空题(本大题共4小题,每小题5分,满分20分)
11. 已知=,则=________.
12. 如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上.已知纸板的两条直角边DE=40cm,EF=20cm,测得边DF离地面的高度AC=1.5 m,CD=8 m,则树高AB=____m.
13. 如图,在反比例函数的图象上有一点A向x轴作垂线交x轴于点C,B为线段的中点,又D点在x轴上,且,则的面积为__________.
14. 已知二次函数(a为常数).则该二次函数的对称轴是__________;当时,y的最小值是,则a的值为__________.
三、(本大题共2小题,每小题8分,满分16分)
15. 已知二次函数y=x2+4x+k-1.
(1)若抛物线与x轴有两个不同的交点,求k的取值范围;
(2)若抛物线的顶点在x轴上,求k的值.
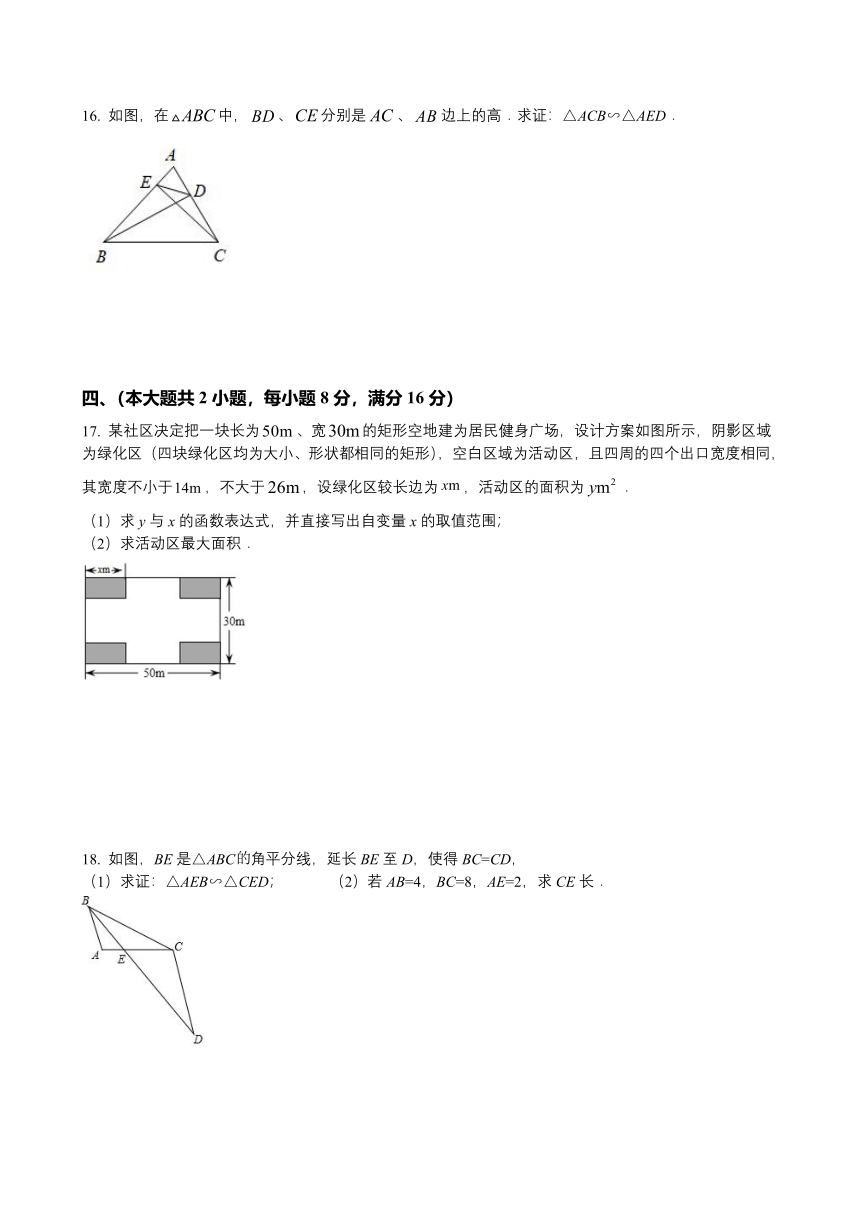
16. 如图,在中,、分别是、边上的高.求证:△ACB∽△AED.
四、(本大题共2小题,每小题8分,满分16分)
17. 某社区决定把一块长为、宽的矩形空地建为居民健身广场,设计方案如图所示,阴影区域为绿化区(四块绿化区均为大小、形状都相同的矩形),空白区域为活动区,且四周的四个出口宽度相同,其宽度不小于,不大于,设绿化区较长边为,活动区的面积为.
(1)求y与x的函数表达式,并直接写出自变量x的取值范围;
(2)求活动区最大面积.
18. 如图,BE是△ABC角平分线,延长BE至D,使得BC=CD,
(1)求证:△AEB∽△CED; (2)若AB=4,BC=8,AE=2,求CE长.
五、(本大题共2小题,每小题10分,满分20分)
19. 如图,点M是AB上一点,AE与BD交于点C,,且DM交AC于F,ME交BC于G. (1)求证:; (2)请你再写出两对相似三角形.
20. 如图,抛物线.与x轴交于A,B两点,与y轴交于直线经过点A且与抛物线交于另一点D.
(1)求抛物线的解析式;
(2)若P是位于直线上方的抛物线上的一个动点,连接,求的面积的最大值.
六、(本题满分12分)
21. 如图,在直角坐标系中,点和点是一次函数和反比例函数图象的交点.
(1)求反比例函数的表达式和点的坐标.
(2)利用图象,直接写出当时的取值范围.
(3)连结并延长交双曲线于点,连结,求面积.
七、(本题满分12分)
22. 如图,点P是菱形ABCD的对角线AC上一点,连接DP并延长,交AB于点F,交CB的延长线于点E. 求证:(1)APB≌APD; (2)PD2=PE PF.
八、(本题满分14分)
23. 某超市拟于中秋节前50天里销售某品牌月饼,其进价为18元/kg.设第x天的销售价格为y(元/kg),销售量为m(kg).该超市根据以往的销售经验得出以下的销售规律:①当1≤x≤30时,y=40;当31≤x≤50时,y与x满足一次函数关系,且当x=36时,y=37;x=44时,y=33.②m与x的关系为m=5x+50.
(1)当31≤x≤50时,求y与x的关系式;
(2)x为多少时,当天的销售利润w(元)最大?最大利润为多少?
(3)若超市希望第31天到第35天的日销售利润W(元)随x的增大而增大,则需要在当天销售价格的基础上涨a元/kg,求a的最小值.
答案
一、选择题(本大题共10小题,每小题4分,满分40分)
1、B 2、C 3、A 4、B 5、D 6、C 7、B 8、A 9、D 10、D
二、填空题(本大题共4小题,每小题5分,满分20分)
11、或填0.25 12、5.5 13、6 14、 ①. ②.
三、(本大题共2小题,每小题8分,满分16分)
15、k<5;k=5. 16、见详解
四、(本大题共2小题,每小题8分,满分16分)
17、(1) (2) 18.(1)见解析;(2)4
五、(本大题共2小题,每小题10分,满分20分)
19、(1)见解析;(2),.
20、(1) (2)
六、(本题满分12分)
21、(1),点的坐标为;(2)或;(3)8
七、(本题满分12分)
22、(1)见解析;(2)见解析
八、(本题满分14分)
23、(1)();(2)当时,w最大值为4410元;(3).
一、选择题(本大题共10小题,每小题4分,满分40分)
1. 将抛物线向左平移4个单位,向上平移1个单位所得新抛物线的表达式为( )
A. y=-2(x-4)2-4 B. y=-2(x+4)2-2 C. y=-2x2+4 D. y=-2x2+4
2. 抛物线的顶点坐标是( )
A. B. C. D.
3. 如图,在中,点P在边上,则在下列四个条件中:;;;, 能满足与相似的条件是( )
A. ①②④ B. ①③④ C. ②③④ D. ①②③
4. 关于x的二次函数,当时,y随x的增大而增大,则实数m的取值范围是( )
A. B. C. D.
5. 对于函数(k<0),下列说法错误的是( )
A. 它的图像分布在二、四象限 B. 它的图像既是轴对称图形又是中心对称图形
C. 当x>0时,y的值随x的增大而增大 D. 当x<0时,y的值随x的增大而减小
6. 如图,AC与BD相交于点E,∠A=∠B,若AE=2,CE=4,DE=3,则BE的长是( )
A 6 B. 4 C. D.
(第3题图) (第6题图) (第9题图) (第10题图)
7. 若点A(-3,y1)、B(-1,y2)、C(3,y3)都在反比例函数(k>0)图象上,则y1、y2、y3的大小关系是( )
A. y1>y2>y 3 B. y3>y1>y2 C. y2>y1>y3 D. y1>y3>y2
8. 在同一平面直角坐标系中,函数y=ax2﹣bx与y=bx+a的图象可能是( )
A. B. C. D.
9. 如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,翻折∠B,使点B落在直角边AC上某一点D处,折痕为EF,点E、F分别在边BC、AB上,若△CDE与△ABC相似,则CE的长为( )
A B. C. 或 D. 或
10. 如图,在△ABC中,∠ACB=90°,AC=4,BC=3,P是AB边上一动点,PD⊥AC于点D,点E在P的右侧,且PE=1,连接CE,P从点A出发,沿AB方向运动,当E到达点B时,P停止运动,在整个运动过程中,阴影部分面积S1+S2的大小变化的情况是( )
A. 一直减小 B. 一直增大 C. 先增大后减小 D. 先减小后增大
二、填空题(本大题共4小题,每小题5分,满分20分)
11. 已知=,则=________.
12. 如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上.已知纸板的两条直角边DE=40cm,EF=20cm,测得边DF离地面的高度AC=1.5 m,CD=8 m,则树高AB=____m.
13. 如图,在反比例函数的图象上有一点A向x轴作垂线交x轴于点C,B为线段的中点,又D点在x轴上,且,则的面积为__________.
14. 已知二次函数(a为常数).则该二次函数的对称轴是__________;当时,y的最小值是,则a的值为__________.
三、(本大题共2小题,每小题8分,满分16分)
15. 已知二次函数y=x2+4x+k-1.
(1)若抛物线与x轴有两个不同的交点,求k的取值范围;
(2)若抛物线的顶点在x轴上,求k的值.
16. 如图,在中,、分别是、边上的高.求证:△ACB∽△AED.
四、(本大题共2小题,每小题8分,满分16分)
17. 某社区决定把一块长为、宽的矩形空地建为居民健身广场,设计方案如图所示,阴影区域为绿化区(四块绿化区均为大小、形状都相同的矩形),空白区域为活动区,且四周的四个出口宽度相同,其宽度不小于,不大于,设绿化区较长边为,活动区的面积为.
(1)求y与x的函数表达式,并直接写出自变量x的取值范围;
(2)求活动区最大面积.
18. 如图,BE是△ABC角平分线,延长BE至D,使得BC=CD,
(1)求证:△AEB∽△CED; (2)若AB=4,BC=8,AE=2,求CE长.
五、(本大题共2小题,每小题10分,满分20分)
19. 如图,点M是AB上一点,AE与BD交于点C,,且DM交AC于F,ME交BC于G. (1)求证:; (2)请你再写出两对相似三角形.
20. 如图,抛物线.与x轴交于A,B两点,与y轴交于直线经过点A且与抛物线交于另一点D.
(1)求抛物线的解析式;
(2)若P是位于直线上方的抛物线上的一个动点,连接,求的面积的最大值.
六、(本题满分12分)
21. 如图,在直角坐标系中,点和点是一次函数和反比例函数图象的交点.
(1)求反比例函数的表达式和点的坐标.
(2)利用图象,直接写出当时的取值范围.
(3)连结并延长交双曲线于点,连结,求面积.
七、(本题满分12分)
22. 如图,点P是菱形ABCD的对角线AC上一点,连接DP并延长,交AB于点F,交CB的延长线于点E. 求证:(1)APB≌APD; (2)PD2=PE PF.
八、(本题满分14分)
23. 某超市拟于中秋节前50天里销售某品牌月饼,其进价为18元/kg.设第x天的销售价格为y(元/kg),销售量为m(kg).该超市根据以往的销售经验得出以下的销售规律:①当1≤x≤30时,y=40;当31≤x≤50时,y与x满足一次函数关系,且当x=36时,y=37;x=44时,y=33.②m与x的关系为m=5x+50.
(1)当31≤x≤50时,求y与x的关系式;
(2)x为多少时,当天的销售利润w(元)最大?最大利润为多少?
(3)若超市希望第31天到第35天的日销售利润W(元)随x的增大而增大,则需要在当天销售价格的基础上涨a元/kg,求a的最小值.
答案
一、选择题(本大题共10小题,每小题4分,满分40分)
1、B 2、C 3、A 4、B 5、D 6、C 7、B 8、A 9、D 10、D
二、填空题(本大题共4小题,每小题5分,满分20分)
11、或填0.25 12、5.5 13、6 14、 ①. ②.
三、(本大题共2小题,每小题8分,满分16分)
15、k<5;k=5. 16、见详解
四、(本大题共2小题,每小题8分,满分16分)
17、(1) (2) 18.(1)见解析;(2)4
五、(本大题共2小题,每小题10分,满分20分)
19、(1)见解析;(2),.
20、(1) (2)
六、(本题满分12分)
21、(1),点的坐标为;(2)或;(3)8
七、(本题满分12分)
22、(1)见解析;(2)见解析
八、(本题满分14分)
23、(1)();(2)当时,w最大值为4410元;(3).
同课章节目录
