14.1.2幂的乘方 课件(共25张PPT)
文档属性
| 名称 | 14.1.2幂的乘方 课件(共25张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-09 17:12:10 | ||
图片预览




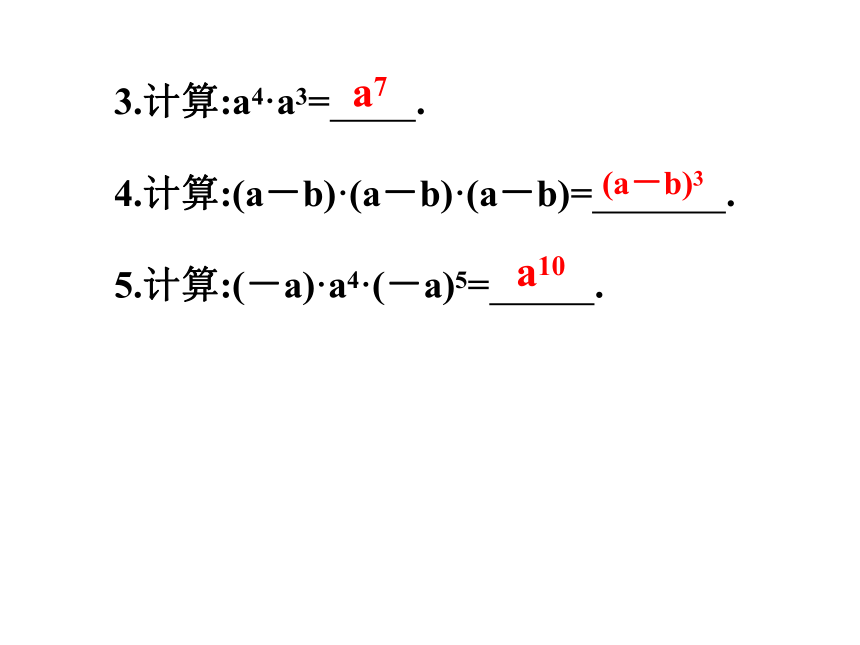




文档简介
(共25张PPT)
人教版 八年级上册
14.1.2 幂的乘方
课件说明
学习目标:
1.理解幂的乘方性质的推导根据.
2.会运用幂的乘方进行计算.
3.在类比同底数幂的乘法性质学习幂的乘方
体会 二者的联系和区别及类比、归纳的
思想方法.
学习重点:幂的乘方的性质.
同底数幂相乘,
底数不变,
指数相加.
(m、n都是正整数).
am an=
am+n
●
复习旧知
1.对于式子34与(-3)4,下列说法正确的是( ).
A.底数相同,指数相同
B.底数不相同,指数相同
C.底数相同,指数不相同
D.底数不相同,指数不相同
2.下列运算正确的是( ).
A.a+b=ab B.x·x=2x
C.x·x·x=x3 D.3a-2a=1
B
C
3.计算:a4·a3= .
4.计算:(a-b)·(a-b)·(a-b)= .
5.计算:(-a)·a4·(-a)5= .
a7
(a-b)3
a10
(1) (32)3 = 32×32 ×32=3( ) ;
观察计算结果,你能发现什么规律?
根据乘方的意义及同底数幂的乘法填空:
(3) (am)3=
(2) (a2)3 =
a2
●
a2
a2
●
=
a( );
am
●
am
am
●
=
a( );
6
6
3m
幂的乘方,
底数不变,
指数相乘。
学习新知
对于任意底数a 与任意正整数m ,n,
(am)n
=
?
(am)n
=
am
●
am
●
●
● ● ●
am
n个am
=
m+m+ +m
● ● ●
n个m
=
amn
a
学习新知
多重乘方可以重复运用上述法则:
幂的乘方性质:
(p是正整数).
(m ,n 都是正整数).
(am)n
=
amn
幂的乘方,
底数不变,
指数相乘.
[(am)n]p
=
amnp
学习新知
例1 计算:
(2) (a4)4;
(3) (am) 2 ;
(1) (103)5;
(4) -(x4)3.
解:
=
10
=
1015;
=
a
=
a16;
=
=
(1) (103)5
(2) (a4)4
(3) (am) 2 =
a
a2m;
(4) -(x4)3=
-
x
-
x12 .
3×5
4×4
m×2
4×3
例题解析
(2) (x3)2;
(1) (103)3;
(3) -(xm)5;
解:
=
=
109;
=
=
x6;
=
=
(1) (103)3
(2) (x3)2
(4) (a2) 3
a6
(3) -(xm)5
-
x5m ;
●
(4) (a2) 3
a5;
●
a5
(5) [(a3)4] 2 ;
(6) 2(am) 2
-
(a2)m .
(5) [(a3)4] 2
(a12)2;
(6) 2(am) 2
-
(a2)m
2a2m
=a24;
a2m
a2m .
-
=
●
a5
a11
=
练习巩固
计算:
(1) (-x3)2;
解:
=
=
-x6;
(1) (- x3)2
a20
(2) (-a5)4
(-a5)3;
●
●
(-a15)
-a35
=
练习巩固
计算:
(3) (a3)2
-
(a3)6 .
(a4)3
●
(2) (-a5)4
(-a5)3
●
(3) (a3)2
-
(a3)6
(a4)3
●
=
a6
a12
●
-a18
=
a18
-a18
=0
例2. 已知 (a)2m =25,
求am的值.
解:
∵ (a)2m = 25,
∴a2m
=
=
±5.
25,
=
52,
∴(am)2
∴ am
例题解析
逆用幂的乘方公式
已知10m=2,
求103m+2n的值.
解:
∵ 10m =2,
∴103m
=
102n =
=
(10m)3
23
=
32
10n=3,
10n =3,
(10n)2
=
9
=
8
=
=
∴103m+2n
103m
102n
8
×9
=72
●
学以致用
例3 若a=355,b=444,c=533,比较a、b、c 的大小.
解:
∵ 355 =
35×11
=
(35)11
=
24311,
444 =
44×11
=
(44)11
=
25611,
533 =
53×11
=
(53)11
=
12511,
而256>243>125,
∴
25611>24311>12511,
即444>355>533,
∴b>a>c.
例题解析
逆用幂的乘方公式
若a=248,b=336,c=524,比较a、b、c 的大小.
解:
∵ 248 =
24×12
=
(24)12
=
1612,
336 =
33×12
=
(33)12
=
2712,
524 =
52×12
=
(52)12
=
2512,
而27>25>16,
∴
2712>2512>1612,
即336>524>248,
∴b>c>a.
学以致用
(1)本节课学习了哪些主要内容?
(2)幂的两个运算性质是什么?它们有什么区别和联系?
课堂小结
(1) x2 · x3= x6
(2) (b2)3=b5
(3) 3a+2a=5a2
(4) (x ) x= x6
判断下列计算是否正确,并简要说明理由:
●
( )
( )
( )
( )
×
×
×
×
练习巩固
1.下列运算正确的是( ).
A. (a ) =a9 B. 2a-a=2
C. (a5)2=a10 D.(a6)6=a12
巩固提高
C
2.计算:(-a5)4·(-a2)3=_______.
-a26
3.辨一辨,填一填:
(1)(-m )4= ;
(2) -(m )4= ;
(3)(-m4) = ;
(4)[(-m)4] = .
m12
-m12
-m12
m12
4. 若3m =2,3n =5,求33m+2n的值.
解:
∴33m+2n
=33m
·32n
=(3)3m
·(3)2n
=(3m)3
·(3n)2
=23
·52
∵3m =2,3n =5,
=8×25
=400.
5.解方程:aa=22048
解:
∵ 22048 =(22)1024
=(4)1024
=(42)512
=(16)512
=(162)256
=(256)256
∴aa=
(256)256
∴a=256.
6.已知:415+ 810=2a.求a的值.
解:
∵ 415 =(22)15
=230,
810 =(23)10
=230,
∴230+ 230=2a
∴2·230=2a
∴231=2a
∴a=31.
今天作业
课本P97页练习
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教版 八年级上册
14.1.2 幂的乘方
课件说明
学习目标:
1.理解幂的乘方性质的推导根据.
2.会运用幂的乘方进行计算.
3.在类比同底数幂的乘法性质学习幂的乘方
体会 二者的联系和区别及类比、归纳的
思想方法.
学习重点:幂的乘方的性质.
同底数幂相乘,
底数不变,
指数相加.
(m、n都是正整数).
am an=
am+n
●
复习旧知
1.对于式子34与(-3)4,下列说法正确的是( ).
A.底数相同,指数相同
B.底数不相同,指数相同
C.底数相同,指数不相同
D.底数不相同,指数不相同
2.下列运算正确的是( ).
A.a+b=ab B.x·x=2x
C.x·x·x=x3 D.3a-2a=1
B
C
3.计算:a4·a3= .
4.计算:(a-b)·(a-b)·(a-b)= .
5.计算:(-a)·a4·(-a)5= .
a7
(a-b)3
a10
(1) (32)3 = 32×32 ×32=3( ) ;
观察计算结果,你能发现什么规律?
根据乘方的意义及同底数幂的乘法填空:
(3) (am)3=
(2) (a2)3 =
a2
●
a2
a2
●
=
a( );
am
●
am
am
●
=
a( );
6
6
3m
幂的乘方,
底数不变,
指数相乘。
学习新知
对于任意底数a 与任意正整数m ,n,
(am)n
=
?
(am)n
=
am
●
am
●
●
● ● ●
am
n个am
=
m+m+ +m
● ● ●
n个m
=
amn
a
学习新知
多重乘方可以重复运用上述法则:
幂的乘方性质:
(p是正整数).
(m ,n 都是正整数).
(am)n
=
amn
幂的乘方,
底数不变,
指数相乘.
[(am)n]p
=
amnp
学习新知
例1 计算:
(2) (a4)4;
(3) (am) 2 ;
(1) (103)5;
(4) -(x4)3.
解:
=
10
=
1015;
=
a
=
a16;
=
=
(1) (103)5
(2) (a4)4
(3) (am) 2 =
a
a2m;
(4) -(x4)3=
-
x
-
x12 .
3×5
4×4
m×2
4×3
例题解析
(2) (x3)2;
(1) (103)3;
(3) -(xm)5;
解:
=
=
109;
=
=
x6;
=
=
(1) (103)3
(2) (x3)2
(4) (a2) 3
a6
(3) -(xm)5
-
x5m ;
●
(4) (a2) 3
a5;
●
a5
(5) [(a3)4] 2 ;
(6) 2(am) 2
-
(a2)m .
(5) [(a3)4] 2
(a12)2;
(6) 2(am) 2
-
(a2)m
2a2m
=a24;
a2m
a2m .
-
=
●
a5
a11
=
练习巩固
计算:
(1) (-x3)2;
解:
=
=
-x6;
(1) (- x3)2
a20
(2) (-a5)4
(-a5)3;
●
●
(-a15)
-a35
=
练习巩固
计算:
(3) (a3)2
-
(a3)6 .
(a4)3
●
(2) (-a5)4
(-a5)3
●
(3) (a3)2
-
(a3)6
(a4)3
●
=
a6
a12
●
-a18
=
a18
-a18
=0
例2. 已知 (a)2m =25,
求am的值.
解:
∵ (a)2m = 25,
∴a2m
=
=
±5.
25,
=
52,
∴(am)2
∴ am
例题解析
逆用幂的乘方公式
已知10m=2,
求103m+2n的值.
解:
∵ 10m =2,
∴103m
=
102n =
=
(10m)3
23
=
32
10n=3,
10n =3,
(10n)2
=
9
=
8
=
=
∴103m+2n
103m
102n
8
×9
=72
●
学以致用
例3 若a=355,b=444,c=533,比较a、b、c 的大小.
解:
∵ 355 =
35×11
=
(35)11
=
24311,
444 =
44×11
=
(44)11
=
25611,
533 =
53×11
=
(53)11
=
12511,
而256>243>125,
∴
25611>24311>12511,
即444>355>533,
∴b>a>c.
例题解析
逆用幂的乘方公式
若a=248,b=336,c=524,比较a、b、c 的大小.
解:
∵ 248 =
24×12
=
(24)12
=
1612,
336 =
33×12
=
(33)12
=
2712,
524 =
52×12
=
(52)12
=
2512,
而27>25>16,
∴
2712>2512>1612,
即336>524>248,
∴b>c>a.
学以致用
(1)本节课学习了哪些主要内容?
(2)幂的两个运算性质是什么?它们有什么区别和联系?
课堂小结
(1) x2 · x3= x6
(2) (b2)3=b5
(3) 3a+2a=5a2
(4) (x ) x= x6
判断下列计算是否正确,并简要说明理由:
●
( )
( )
( )
( )
×
×
×
×
练习巩固
1.下列运算正确的是( ).
A. (a ) =a9 B. 2a-a=2
C. (a5)2=a10 D.(a6)6=a12
巩固提高
C
2.计算:(-a5)4·(-a2)3=_______.
-a26
3.辨一辨,填一填:
(1)(-m )4= ;
(2) -(m )4= ;
(3)(-m4) = ;
(4)[(-m)4] = .
m12
-m12
-m12
m12
4. 若3m =2,3n =5,求33m+2n的值.
解:
∴33m+2n
=33m
·32n
=(3)3m
·(3)2n
=(3m)3
·(3n)2
=23
·52
∵3m =2,3n =5,
=8×25
=400.
5.解方程:aa=22048
解:
∵ 22048 =(22)1024
=(4)1024
=(42)512
=(16)512
=(162)256
=(256)256
∴aa=
(256)256
∴a=256.
6.已知:415+ 810=2a.求a的值.
解:
∵ 415 =(22)15
=230,
810 =(23)10
=230,
∴230+ 230=2a
∴2·230=2a
∴231=2a
∴a=31.
今天作业
课本P97页练习
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
