14.1.3积的乘方 课件(共25张PPT)
文档属性
| 名称 | 14.1.3积的乘方 课件(共25张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-09 00:00:00 | ||
图片预览








文档简介
(共25张PPT)
人教版 八年级上册
14.1.3 积的乘方
课件说明
学习目标:
1.理解积的乘方性质的推导根据.
2.会运用积的乘方性质进行计算.
3.在类比同底数幂的乘法性质学习与积的乘方性
质,体会二者的联系和区别及类比、归纳的思想方法.
学习重点:
积的乘方的性质.
1.同底数幂相乘,
底数不变,
指数相加.
(m、n都是正整数).
am an=
am+n
●
复习旧知
幂运算法则
(m ,n 都是正整数).
(am)n
=
amn
2.幂的乘方,
底数不变,
指数相乘.
1.下列计算中正确的是( ).
A. a2+a3=2a5 B.a4·a=a4
C.a2·a4=a8 D.(-a2)3=-a6
2.化简(-x)3·(-x)2的结果正确的是 ( ).
A. -x6 B. x6
C. x5 D. -x5
D
D
3.若3x=15, 3y=5,则3x+y等于( ).
A.10 B.20
C.60 D.75
4.化简(-a2)3·(-a3)2的结果是 .
D
-a12
你能发现有何运算规律吗?
根据乘方的意义和乘法的运算律计算:
(1) (ab)2 =
(ab)
●
(ab)
=
(a
●
a)
(2)
●
(ab)3=
(b
●
b)
=
a( )
b( );
(ab)
(a
●
a a)
●
(ab)
●
(ab)
●
=
●
(b
●
b b)
●
=
a( )
b( )
2
2
3
3
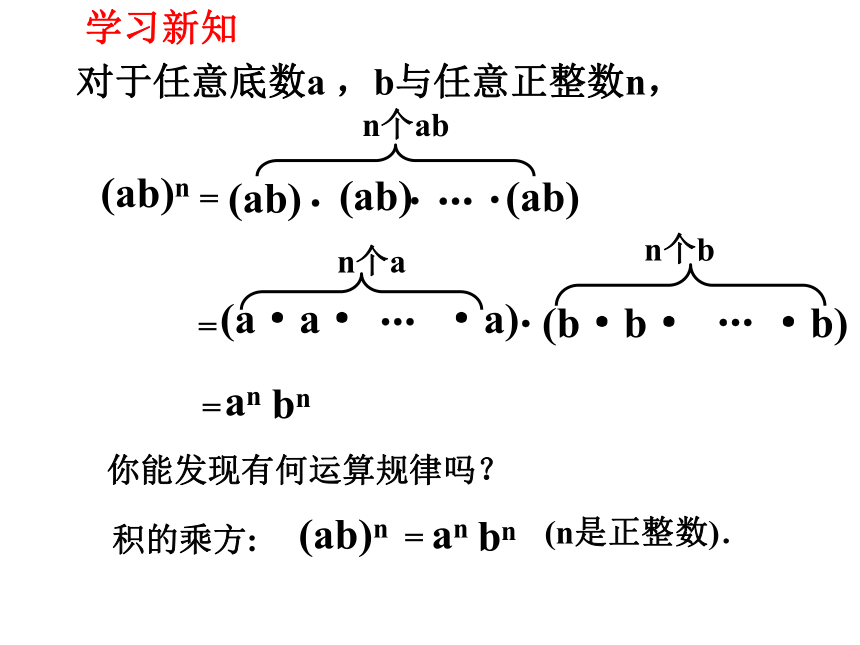
学习新知
对于任意底数a ,b与任意正整数n,
=
●
● ● ●
n个ab
=
n个a
=
an
(ab)n
(ab)
●
(ab)
●
(ab)
●
(a·a· ·a)
● ● ●
(b·b· ·b)
● ● ●
n个b
bn
你能发现有何运算规律吗?
积的乘方:
=
an
(ab)n
bn
(n是正整数).
学习新知
当n 是正整数时,三个或三个以上因式的积的乘
方,也具有这一性质吗?
积的乘方,等于把积的每一个因式分别乘方,再
把所得的幂相乘.
推广:
能用文字语言概述你发现的积的乘方运算规律吗?
=
an
(abc)n =
bn
(ab)n
bn
cn
an
学习新知
例1 计算:
(2) (-5b)3;
(3) (xy2) 2 ;
(1) (2a)3;
(4) (-2x3 )4.
解:
=
=
8a3;
=
=
b3;
=
=
(1) (2a)3
(2) (-5b)3
(3) (xy2) 2 =
x2y4;
(4) (-2x 3) 4 =
(-2)4
16
x12 .
23
●
a3
(-5)3
●
b3
-125
x2
●
(y2)2
●
(x3)4
例题解析
计算:
(2) (- xy)3;
(4) (2ab2) 3 .
(1) (ab)4;
(3) ( - 3×102 )3;
解:
=
a4b4;
=
x3y3;
=
=
(1) (ab)4
(2) (- xy)3
(4) (2ab2) 3 =
(2)3
8
a3b6 .
-
(b2)3
●
(a)3
1
2
1
2
1
8
(3) ( -3×102 )3
(-3)3×(102 )3
=
- 27×106
=
=
(- )3
(xy)3
1
2
- 2.7×107;
练习巩固
计算:
(1) ( -3a4bc2 )3;
解:
(2) (- x3y)3 (-2xy)5
●
1
2
练习巩固
(1) ( -3a4bc2 )3=
(-3)3
b3
(a4)3
(c2)3
=-27
a12b3
c6
(2) (- x3y)3 (-2xy)5
●
1
2
=(- )3
(x3)3y3
(-2)5
x5y5
1
2
=
1
8
-
x9y3
●
(-32)
x5y5
=
4x14y8
解:
答:所得的铁盒的容积是a3b3.
一个边长为a 的正方体铁盒,现将它的边
长变为原来的b 倍,所得的铁盒的容积是多少?
(ab)3
=
ab
●
ab
ab
●
=
a3b3
练习巩固
2.下列计算正确的是( ).
A. 3a+2b=5ab B. (2ab3)2=2a2b6
C. (-2)2×(-2)3=-26 D. (-a3b)2=a6b2
1.下列运算正确的是( ).
A.x2+x2=2x4 B.a·a4=a4
C.x2·x2=2x3 D.(-2x2)3=-8x6
D
D
练习巩固
计算:
0.252022×(-4)2022×0.1252023 ×(-8)2024
解:
原式=
[0.25×(-4)]2022
×(-8)
=
1
×(-1)
×(-8)
=
8
[0.125× (-8)]2023
×
新知拓展
逆用积的乘方法则
计算:
2100×( )100×( )10 ×( )9
解:
原式=
[2× ]100
×( )
=
1
×1
×
=
( × )9
×
学以致用
1
2
3
5
5
3
1
2
3
5
5
3
3
5
3
5
3
5
(1)本节课学习了哪些主要内容?
(2)幂的三个运算性质是什么?它们有什么区别和联系?
课堂小结
1.下列运算正确的是( ).
A.a a3=a3 B.(ab)3=ab3
C.a3+a3=a6: D.(a3)3=a9
2.计算(-4a)2的结果是( ).
A. -8a2 B.8a2
C. -16a2 D.16a2
●
巩固提高
D
D
3.计算(3×106) 的结果是( ).
A.9×109 B.2.7×1019
C.9×1018 D.2.7×1010
B
4.计算(- 4×103)2×(-2×103)3的
正确结果是( ).
A .-1.28×1017. B.4.8×1016
C.1.08×1017 D. 1.28×1017
A
5. 已知(ambn )3=a6b12,求mn的算术平方根.
。
解:
∵(ambn )3=a6b12,
∴a3mb3n =a6b12
∴3m=6,
3n=12,
∴m=2,
n=4,
∴mn
=24
=16.
∴mn的算术平方根为4.
∵16的算术平方根为4,
6.计算:523×167
解:
523×167
=523×(24)7
=523×228
=523×223
×25
=(5×2)23
×25
=1023
×32
=3.2×1024
7.已知:89=a ,98=b.求7272.
解:
7272
=(8×9)72
=872×972
=89×8×98×9
=(89)8×(98) 9
=a8b9
今天作业
课本P104页第1、2题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教版 八年级上册
14.1.3 积的乘方
课件说明
学习目标:
1.理解积的乘方性质的推导根据.
2.会运用积的乘方性质进行计算.
3.在类比同底数幂的乘法性质学习与积的乘方性
质,体会二者的联系和区别及类比、归纳的思想方法.
学习重点:
积的乘方的性质.
1.同底数幂相乘,
底数不变,
指数相加.
(m、n都是正整数).
am an=
am+n
●
复习旧知
幂运算法则
(m ,n 都是正整数).
(am)n
=
amn
2.幂的乘方,
底数不变,
指数相乘.
1.下列计算中正确的是( ).
A. a2+a3=2a5 B.a4·a=a4
C.a2·a4=a8 D.(-a2)3=-a6
2.化简(-x)3·(-x)2的结果正确的是 ( ).
A. -x6 B. x6
C. x5 D. -x5
D
D
3.若3x=15, 3y=5,则3x+y等于( ).
A.10 B.20
C.60 D.75
4.化简(-a2)3·(-a3)2的结果是 .
D
-a12
你能发现有何运算规律吗?
根据乘方的意义和乘法的运算律计算:
(1) (ab)2 =
(ab)
●
(ab)
=
(a
●
a)
(2)
●
(ab)3=
(b
●
b)
=
a( )
b( );
(ab)
(a
●
a a)
●
(ab)
●
(ab)
●
=
●
(b
●
b b)
●
=
a( )
b( )
2
2
3
3
学习新知
对于任意底数a ,b与任意正整数n,
=
●
● ● ●
n个ab
=
n个a
=
an
(ab)n
(ab)
●
(ab)
●
(ab)
●
(a·a· ·a)
● ● ●
(b·b· ·b)
● ● ●
n个b
bn
你能发现有何运算规律吗?
积的乘方:
=
an
(ab)n
bn
(n是正整数).
学习新知
当n 是正整数时,三个或三个以上因式的积的乘
方,也具有这一性质吗?
积的乘方,等于把积的每一个因式分别乘方,再
把所得的幂相乘.
推广:
能用文字语言概述你发现的积的乘方运算规律吗?
=
an
(abc)n =
bn
(ab)n
bn
cn
an
学习新知
例1 计算:
(2) (-5b)3;
(3) (xy2) 2 ;
(1) (2a)3;
(4) (-2x3 )4.
解:
=
=
8a3;
=
=
b3;
=
=
(1) (2a)3
(2) (-5b)3
(3) (xy2) 2 =
x2y4;
(4) (-2x 3) 4 =
(-2)4
16
x12 .
23
●
a3
(-5)3
●
b3
-125
x2
●
(y2)2
●
(x3)4
例题解析
计算:
(2) (- xy)3;
(4) (2ab2) 3 .
(1) (ab)4;
(3) ( - 3×102 )3;
解:
=
a4b4;
=
x3y3;
=
=
(1) (ab)4
(2) (- xy)3
(4) (2ab2) 3 =
(2)3
8
a3b6 .
-
(b2)3
●
(a)3
1
2
1
2
1
8
(3) ( -3×102 )3
(-3)3×(102 )3
=
- 27×106
=
=
(- )3
(xy)3
1
2
- 2.7×107;
练习巩固
计算:
(1) ( -3a4bc2 )3;
解:
(2) (- x3y)3 (-2xy)5
●
1
2
练习巩固
(1) ( -3a4bc2 )3=
(-3)3
b3
(a4)3
(c2)3
=-27
a12b3
c6
(2) (- x3y)3 (-2xy)5
●
1
2
=(- )3
(x3)3y3
(-2)5
x5y5
1
2
=
1
8
-
x9y3
●
(-32)
x5y5
=
4x14y8
解:
答:所得的铁盒的容积是a3b3.
一个边长为a 的正方体铁盒,现将它的边
长变为原来的b 倍,所得的铁盒的容积是多少?
(ab)3
=
ab
●
ab
ab
●
=
a3b3
练习巩固
2.下列计算正确的是( ).
A. 3a+2b=5ab B. (2ab3)2=2a2b6
C. (-2)2×(-2)3=-26 D. (-a3b)2=a6b2
1.下列运算正确的是( ).
A.x2+x2=2x4 B.a·a4=a4
C.x2·x2=2x3 D.(-2x2)3=-8x6
D
D
练习巩固
计算:
0.252022×(-4)2022×0.1252023 ×(-8)2024
解:
原式=
[0.25×(-4)]2022
×(-8)
=
1
×(-1)
×(-8)
=
8
[0.125× (-8)]2023
×
新知拓展
逆用积的乘方法则
计算:
2100×( )100×( )10 ×( )9
解:
原式=
[2× ]100
×( )
=
1
×1
×
=
( × )9
×
学以致用
1
2
3
5
5
3
1
2
3
5
5
3
3
5
3
5
3
5
(1)本节课学习了哪些主要内容?
(2)幂的三个运算性质是什么?它们有什么区别和联系?
课堂小结
1.下列运算正确的是( ).
A.a a3=a3 B.(ab)3=ab3
C.a3+a3=a6: D.(a3)3=a9
2.计算(-4a)2的结果是( ).
A. -8a2 B.8a2
C. -16a2 D.16a2
●
巩固提高
D
D
3.计算(3×106) 的结果是( ).
A.9×109 B.2.7×1019
C.9×1018 D.2.7×1010
B
4.计算(- 4×103)2×(-2×103)3的
正确结果是( ).
A .-1.28×1017. B.4.8×1016
C.1.08×1017 D. 1.28×1017
A
5. 已知(ambn )3=a6b12,求mn的算术平方根.
。
解:
∵(ambn )3=a6b12,
∴a3mb3n =a6b12
∴3m=6,
3n=12,
∴m=2,
n=4,
∴mn
=24
=16.
∴mn的算术平方根为4.
∵16的算术平方根为4,
6.计算:523×167
解:
523×167
=523×(24)7
=523×228
=523×223
×25
=(5×2)23
×25
=1023
×32
=3.2×1024
7.已知:89=a ,98=b.求7272.
解:
7272
=(8×9)72
=872×972
=89×8×98×9
=(89)8×(98) 9
=a8b9
今天作业
课本P104页第1、2题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
