高中数学必修第一册人教A版(2019)5.3《诱导公式---第二课时》名师课件(共27张PPT)
文档属性
| 名称 | 高中数学必修第一册人教A版(2019)5.3《诱导公式---第二课时》名师课件(共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-09 06:42:47 | ||
图片预览






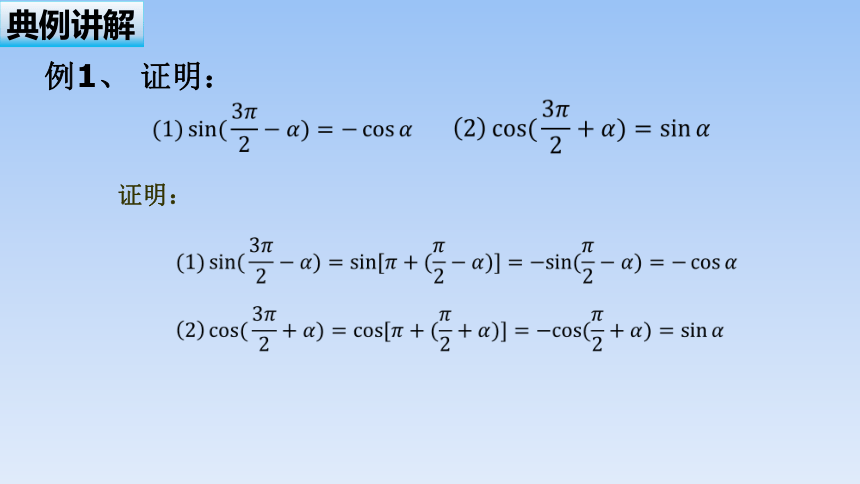

文档简介
(共27张PPT)
公式一
公式二
公式三
公式四
复习引入
人教A版同步教材名师课件
诱导公式---第二课时
学习目标
学 习 目 标 核心素养
通过本节内容的学习,学会推导并理解诱导公式,总结这些诱导公式的特征与规律,理解“奇变偶不变,符号看象限”的准确含义. 数学抽象
通过本节的学习,熟练运用诱导公式进行简单三角函数式的化简、求值与证明. 逻辑推理
学习目标
课程目标
1.借助单位圆,推导出正弦、余弦第二、三、四、五、六组的诱导公式,能正确运用诱导公式将任意角的三角函数化为锐角的三角函数,并解决有关三角函数求值、化简和恒等式证明问题.
2.通过公式的应用,了解未知到已知、复杂到简单的转化过程,培养学生的化归思想,以及信息加工能力、运算推理能力、分析问题和解决问题的能力.
数学学科素养
1.数学抽象:理解六组诱导公式;
2.逻辑推理:借助单位圆中三角函数的定义推导出六组诱导公式;
3.数学运算:利用六组诱导公式进行化简、求值与恒等式证明.
o
x
y
P(x,y)
P’(y,x)
M
N
的
终边
的
终边
终边关于直线对称
探究1、角与的终边有何位置关系
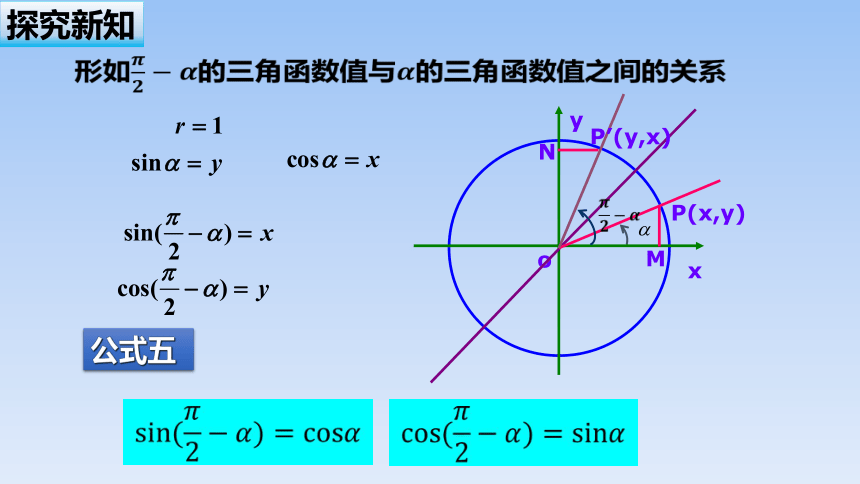
探究新知
公式五
o
x
y
P(x,y)
P’(y,x)
M
N
形如的三角函数值与的三角函数值之间的关系
探究新知
公式六
o
x
y
P(x,y)
P’(y,x)
P’’(-y,x)
探究2、角与的终边有何位置关系
探究新知
例1、 证明:
证明:
典例讲解
典例讲解
例2、已知则的值等于( )
解析
因为,所以.
利用先将角进行转化,再利用诱导公式求值.
思路分析
A
方法归纳
给值求值问题的求解思路
已知角A的三角函数值,求角B的三角函数值,当不能将A,B均转化为与另一角有关的三角函数时,可考虑采用整体处理法.观察已知角A与所求角B的和或差,看能否等于等,如果能,可把角B的三角函数用角A的三角函数表示,进而代入求值.
步骤如下:
(1)寻关系:确定已知式中的角与所求式子中的角的关系.(2)选公式:根据两角之间的关系选择合理的诱导公式.
(3)得结论:根据选择的诱导公式,得到已知式与所求式之间的关系,从而得到答案.
变式训练
1.,则
因为,,
所以
故选A.
解析
变式训练
2.设,则_________.
解析
由,得,
又,把代入,得原式.
变式训练
解析
,
,且
原式,把代入,得原式.
典例讲解
例3、已知
解析
由题意,得,得
.
,.
把代入②,得,又∵0 < < π,= ;
把代入②,得,又∵ 0 < < π ,.
综上,,= 或,.
先用诱导公式进行化简,然后利用方程(组)求解得到角α的一个三角函数值,最后利用范围求解.
思路分析
方法归纳
(1)化简题目中的条件,求出角的某个三角函数值;
(2)结合特殊角的三角函数值逆向求角,表示出符合条件的角;
(3)依据题目条件中角的对应范围求得相应角的值.
给值求角问题的解题方法
变式训练
4. ,
, .
解析
典例讲解
例4、化简:.
解析
原式.
方法归纳
化简是一种不指明答案的恒等变形,将三角函数式化为最简形式的标准是相对的,一般是指函数种类最少,项数最少,函数次数最低,能求出数值的求出数值,分母上不含三角函数和根式,三角函数式化简主要采用“异角化同角、异名化同名”的解题策略.
变式训练
5.化简:
.
原式
解析
典例讲解
例5、求证.
解析
左边右边,
原等式得证.
观察被证等式两端,左繁右简,可以从左端入手,利用诱导公式进行化简,逐步地推向右边.
思路分析
方法归纳
(1)直接证明法:即从一边开始,证得它等于另一边,一般由繁到简;
(2)左右归一法:即证明左右两边都等于同个式子;
(3)作差法:即证明“”;
(4)作商法:即证明 = 1,且右边 ≠ 0.
无论用哪种方法都要针对题设与结论间的差异,有针对性地变形.
关于无条件三角恒等式证明的常用方法
变式训练
6.求证:
.
(1)左边
(2)左边,,
左边=右边,故原等式成立.
解析
1.诱导公式五、六
素养提炼
(1)诱导公式一~六揭示了终边具有某种对称关系的两个角的三角函数之间的关系.
(2)这六组诱导公式可归纳为“k·90°±α(k∈Z)”的三角函数值与α的三角函数值之间的关系.当k为偶数时得角α的同名三角函数值,当k为奇数时得角α的异名三角函数值.然后在前面加上一个把角α看成锐角时原三角函数值的符号.可简记为“奇变偶不变,符号看象限”.
2.诱导公式一~六
素养提炼
当堂练习
1.若
A.第一象限角 B.第二象限角 C.第三象限角 D.第四象限角
2.下列与的值相等的式子为( )
A. B.C. D.s
3.如果,那么
4.已知 = ,则的值为( )
B
D
B
A
归纳小结
诱导公式
公式五
公式六
的正弦(余弦)函数值,分别等于的余弦(正弦)函数值,前面加上个把α看成锐角时原函数值的符号
作 业
P194练习:2、3
公式一
公式二
公式三
公式四
复习引入
人教A版同步教材名师课件
诱导公式---第二课时
学习目标
学 习 目 标 核心素养
通过本节内容的学习,学会推导并理解诱导公式,总结这些诱导公式的特征与规律,理解“奇变偶不变,符号看象限”的准确含义. 数学抽象
通过本节的学习,熟练运用诱导公式进行简单三角函数式的化简、求值与证明. 逻辑推理
学习目标
课程目标
1.借助单位圆,推导出正弦、余弦第二、三、四、五、六组的诱导公式,能正确运用诱导公式将任意角的三角函数化为锐角的三角函数,并解决有关三角函数求值、化简和恒等式证明问题.
2.通过公式的应用,了解未知到已知、复杂到简单的转化过程,培养学生的化归思想,以及信息加工能力、运算推理能力、分析问题和解决问题的能力.
数学学科素养
1.数学抽象:理解六组诱导公式;
2.逻辑推理:借助单位圆中三角函数的定义推导出六组诱导公式;
3.数学运算:利用六组诱导公式进行化简、求值与恒等式证明.
o
x
y
P(x,y)
P’(y,x)
M
N
的
终边
的
终边
终边关于直线对称
探究1、角与的终边有何位置关系
探究新知
公式五
o
x
y
P(x,y)
P’(y,x)
M
N
形如的三角函数值与的三角函数值之间的关系
探究新知
公式六
o
x
y
P(x,y)
P’(y,x)
P’’(-y,x)
探究2、角与的终边有何位置关系
探究新知
例1、 证明:
证明:
典例讲解
典例讲解
例2、已知则的值等于( )
解析
因为,所以.
利用先将角进行转化,再利用诱导公式求值.
思路分析
A
方法归纳
给值求值问题的求解思路
已知角A的三角函数值,求角B的三角函数值,当不能将A,B均转化为与另一角有关的三角函数时,可考虑采用整体处理法.观察已知角A与所求角B的和或差,看能否等于等,如果能,可把角B的三角函数用角A的三角函数表示,进而代入求值.
步骤如下:
(1)寻关系:确定已知式中的角与所求式子中的角的关系.(2)选公式:根据两角之间的关系选择合理的诱导公式.
(3)得结论:根据选择的诱导公式,得到已知式与所求式之间的关系,从而得到答案.
变式训练
1.,则
因为,,
所以
故选A.
解析
变式训练
2.设,则_________.
解析
由,得,
又,把代入,得原式.
变式训练
解析
,
,且
原式,把代入,得原式.
典例讲解
例3、已知
解析
由题意,得,得
.
,.
把代入②,得,又∵0 < < π,= ;
把代入②,得,又∵ 0 < < π ,.
综上,,= 或,.
先用诱导公式进行化简,然后利用方程(组)求解得到角α的一个三角函数值,最后利用范围求解.
思路分析
方法归纳
(1)化简题目中的条件,求出角的某个三角函数值;
(2)结合特殊角的三角函数值逆向求角,表示出符合条件的角;
(3)依据题目条件中角的对应范围求得相应角的值.
给值求角问题的解题方法
变式训练
4. ,
, .
解析
典例讲解
例4、化简:.
解析
原式.
方法归纳
化简是一种不指明答案的恒等变形,将三角函数式化为最简形式的标准是相对的,一般是指函数种类最少,项数最少,函数次数最低,能求出数值的求出数值,分母上不含三角函数和根式,三角函数式化简主要采用“异角化同角、异名化同名”的解题策略.
变式训练
5.化简:
.
原式
解析
典例讲解
例5、求证.
解析
左边右边,
原等式得证.
观察被证等式两端,左繁右简,可以从左端入手,利用诱导公式进行化简,逐步地推向右边.
思路分析
方法归纳
(1)直接证明法:即从一边开始,证得它等于另一边,一般由繁到简;
(2)左右归一法:即证明左右两边都等于同个式子;
(3)作差法:即证明“”;
(4)作商法:即证明 = 1,且右边 ≠ 0.
无论用哪种方法都要针对题设与结论间的差异,有针对性地变形.
关于无条件三角恒等式证明的常用方法
变式训练
6.求证:
.
(1)左边
(2)左边,,
左边=右边,故原等式成立.
解析
1.诱导公式五、六
素养提炼
(1)诱导公式一~六揭示了终边具有某种对称关系的两个角的三角函数之间的关系.
(2)这六组诱导公式可归纳为“k·90°±α(k∈Z)”的三角函数值与α的三角函数值之间的关系.当k为偶数时得角α的同名三角函数值,当k为奇数时得角α的异名三角函数值.然后在前面加上一个把角α看成锐角时原三角函数值的符号.可简记为“奇变偶不变,符号看象限”.
2.诱导公式一~六
素养提炼
当堂练习
1.若
A.第一象限角 B.第二象限角 C.第三象限角 D.第四象限角
2.下列与的值相等的式子为( )
A. B.C. D.s
3.如果,那么
4.已知 = ,则的值为( )
B
D
B
A
归纳小结
诱导公式
公式五
公式六
的正弦(余弦)函数值,分别等于的余弦(正弦)函数值,前面加上个把α看成锐角时原函数值的符号
作 业
P194练习:2、3
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
