24[1].1 圆综合训练(含答案)-.doc[上学期]
文档属性
| 名称 | 24[1].1 圆综合训练(含答案)-.doc[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 41.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-10-10 00:00:00 | ||
图片预览


文档简介
24.1 圆综合训练 ( http: / / )
(检测时间:45分钟 满分:100分)
班级_______________ 姓名________________ 得分_______
一、填空题(4分×6=24分)
1.经过一点可以作________个圆;经过两点可以作_______个圆,这些圆的圆心在这两点连线的_______上;经过不在同一直线上的三点可以作_____个圆,并且只_______圆.
2.如图1,已知△ABC中,∠ACB=90°,∠B=35°,以C为圆心,CA为半径的圆交AB于D 点,则弧AD所对的圆心角的度数为________.
( http: / / )
(1) (2) (3) (4)
3.如图2,已知⊙O中,OD⊥BC于D,∠BOD=48°,则∠BAC=_______.
4.如图3,在⊙O中,所对的圆心角有_______个;所对的圆周角有______;弧AB所对的圆心角有______个;弧AB所对的圆周角有________个.
5.如图4所示,AB是⊙O的直径,,∠A=25°,则∠BOD=_______.
6.如图5,已知AB是⊙O的直径,D是圆上任意一点(不与A、B重合),连接BD,并延长到C,使DC=BD,连接AC则△ABC的形状为________三角形.
( http: / / )
(5) (6) (7) (8)
二、选择题(4分×7=28分)
7.下列命题中,不正确的是( )
A.圆是轴对称图形; B.圆是中心对称图形;
C.圆既是轴对称图形,又是中心对称图形;
D.圆既不是轴对称图形,又不是中心对称图形
8.已知⊙O的半径为2cm,圆心角∠AOB=90°,则弦AB的长为( )
A.4cm B.cm C.3cm D.2cm
9.如图6,DE是⊙O的直径,弦AB⊥ED于C,连接AE、BE、AO、BO,则图中全等三角形的对数有( )
A.3对 B.2对 C.1对 D.0对
10.一条弧所对的圆心角是30°,则它所对的圆周角是( )
A.15° B.30° C.60° D.不能确定
11.如图7,AB为⊙O的直径,CD为弦,其中相等的圆周角共有( )
A.3对 B.4对 C.5对 D.6对
12.如图8,C是⊙O上的一点,O是圆心,若∠C=35°,则∠AOB的度数为( )
A.35° B.70° C.105° D.150°
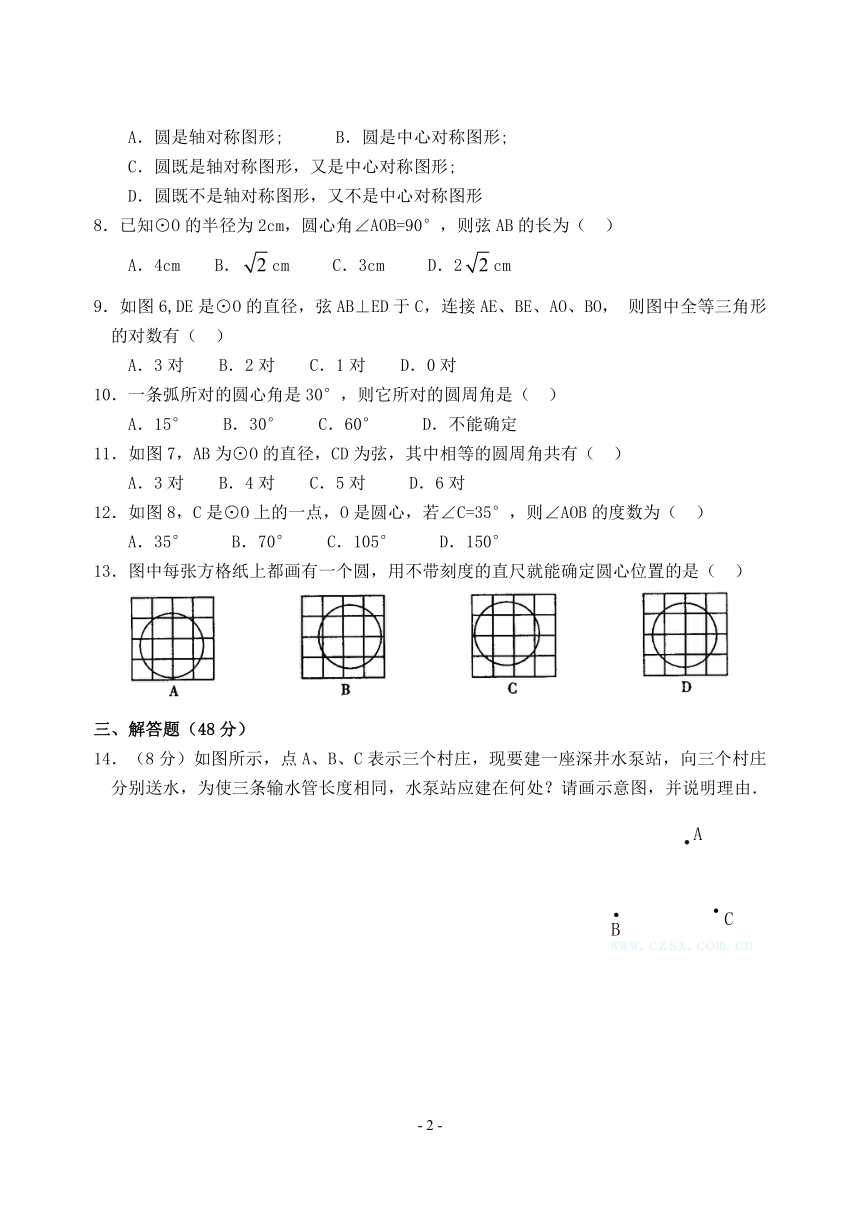
13.图中每张方格纸上都画有一个圆,用不带刻度的直尺就能确定圆心位置的是( )
( http: / / )
三、解答题(48分)
14.(8分)如图所示,点A、B、C表示三个村庄,现要建一座深井水泵站,向三个村庄分别送水,为使三条输水管长度相同,水泵站应建在何处?请画示意图,并说明理由.
15.(8分)如图所示,自⊙O上一点C向弦AB作垂线段CD,求证∠ACD=∠BCO.
16.(10分)如图所示,已知△ABC内接于⊙O,AB=AC,∠BOC=120°.
(1)求证△ABC为等边三角形;(2)试求∠BAD的度数.
17.(10分)如图,在△ABC中,以BC为直径的⊙O交AB于D、交AC于E,且BD=EC.
求证:AB=AC.
18.(12分)如图,点P是圆上的一个动点,弦AB=,PC是∠APB的平分线,∠BAC=30°.
(1)当∠PAC等于多少度时,四边形PACB有最大面积?最大面积是多少?
(2)当∠PAC等于多少度时,四边形PACB是梯形?说明你的理由.
答案:
1.无数 无数 垂直平分线 一 能作一个 2.70° 3.48°
4.1 无数 1 无数 5.50° 6.等腰
7.D 8.D 9.A 10.A 11.C 12.B 13.D
14.略 15.提示:连接OB,∵OC=OB,
∴∠OCB=∠OBC=(180°-∠BOC)=90°-∠BOC,
而∠ACD=90°-∠A,∵∠BOC=2∠A,
∴∠BCO=90°-∠BOC=90°-∠A,∴∠ACD=∠BCO.
16.(1)证明:∵∠BOC=120°,
∴∠BAC=∠BOC=60°,
又∵AB=AC,∴△ABC是等边三角形.
(2)∠BAD=90°
17.证明:连结OD、OE,∵BD=EC,
∴∠BOD=∠COE,
又OB=OC,OD=OE,
∴△BOD≌△COE,
∴∠B=∠C,∴AB=AC.
18.(1)∵PC是∠APB的平分线,
∴,当PC是圆的直径,
即∠PAC=90°时,四边形PACB面积最大,
在Rt△PAC中,∠APC=30°,AP=PB=AB=,
∴PC=2,
∴S四边形PACB=2S△ACP=PC·AB=×2×=.
(2)当∠PAC=120°时,四边形PACB是梯形,
∵PC是∠APB的平分线,∴∠APC=∠BPC=∠CAB=30°,
∴∠APB=60°,∴∠PAC+∠APB=180°,
∴AC∥PB.且AP与BC不平行,
∴四边形PACB是梯形,
当∠PAC=60°时,四边形PACB是梯形,
∵,∴AC=BC,
又∵∠BAC=30°,∴∠ACB=120°,
∴∠PAC+∠ACB=180°,
∴BC∥AP且AC与PB不平行,
∴四边形PACB是梯形.
- 1 -
(检测时间:45分钟 满分:100分)
班级_______________ 姓名________________ 得分_______
一、填空题(4分×6=24分)
1.经过一点可以作________个圆;经过两点可以作_______个圆,这些圆的圆心在这两点连线的_______上;经过不在同一直线上的三点可以作_____个圆,并且只_______圆.
2.如图1,已知△ABC中,∠ACB=90°,∠B=35°,以C为圆心,CA为半径的圆交AB于D 点,则弧AD所对的圆心角的度数为________.
( http: / / )
(1) (2) (3) (4)
3.如图2,已知⊙O中,OD⊥BC于D,∠BOD=48°,则∠BAC=_______.
4.如图3,在⊙O中,所对的圆心角有_______个;所对的圆周角有______;弧AB所对的圆心角有______个;弧AB所对的圆周角有________个.
5.如图4所示,AB是⊙O的直径,,∠A=25°,则∠BOD=_______.
6.如图5,已知AB是⊙O的直径,D是圆上任意一点(不与A、B重合),连接BD,并延长到C,使DC=BD,连接AC则△ABC的形状为________三角形.
( http: / / )
(5) (6) (7) (8)
二、选择题(4分×7=28分)
7.下列命题中,不正确的是( )
A.圆是轴对称图形; B.圆是中心对称图形;
C.圆既是轴对称图形,又是中心对称图形;
D.圆既不是轴对称图形,又不是中心对称图形
8.已知⊙O的半径为2cm,圆心角∠AOB=90°,则弦AB的长为( )
A.4cm B.cm C.3cm D.2cm
9.如图6,DE是⊙O的直径,弦AB⊥ED于C,连接AE、BE、AO、BO,则图中全等三角形的对数有( )
A.3对 B.2对 C.1对 D.0对
10.一条弧所对的圆心角是30°,则它所对的圆周角是( )
A.15° B.30° C.60° D.不能确定
11.如图7,AB为⊙O的直径,CD为弦,其中相等的圆周角共有( )
A.3对 B.4对 C.5对 D.6对
12.如图8,C是⊙O上的一点,O是圆心,若∠C=35°,则∠AOB的度数为( )
A.35° B.70° C.105° D.150°
13.图中每张方格纸上都画有一个圆,用不带刻度的直尺就能确定圆心位置的是( )
( http: / / )
三、解答题(48分)
14.(8分)如图所示,点A、B、C表示三个村庄,现要建一座深井水泵站,向三个村庄分别送水,为使三条输水管长度相同,水泵站应建在何处?请画示意图,并说明理由.
15.(8分)如图所示,自⊙O上一点C向弦AB作垂线段CD,求证∠ACD=∠BCO.
16.(10分)如图所示,已知△ABC内接于⊙O,AB=AC,∠BOC=120°.
(1)求证△ABC为等边三角形;(2)试求∠BAD的度数.
17.(10分)如图,在△ABC中,以BC为直径的⊙O交AB于D、交AC于E,且BD=EC.
求证:AB=AC.
18.(12分)如图,点P是圆上的一个动点,弦AB=,PC是∠APB的平分线,∠BAC=30°.
(1)当∠PAC等于多少度时,四边形PACB有最大面积?最大面积是多少?
(2)当∠PAC等于多少度时,四边形PACB是梯形?说明你的理由.
答案:
1.无数 无数 垂直平分线 一 能作一个 2.70° 3.48°
4.1 无数 1 无数 5.50° 6.等腰
7.D 8.D 9.A 10.A 11.C 12.B 13.D
14.略 15.提示:连接OB,∵OC=OB,
∴∠OCB=∠OBC=(180°-∠BOC)=90°-∠BOC,
而∠ACD=90°-∠A,∵∠BOC=2∠A,
∴∠BCO=90°-∠BOC=90°-∠A,∴∠ACD=∠BCO.
16.(1)证明:∵∠BOC=120°,
∴∠BAC=∠BOC=60°,
又∵AB=AC,∴△ABC是等边三角形.
(2)∠BAD=90°
17.证明:连结OD、OE,∵BD=EC,
∴∠BOD=∠COE,
又OB=OC,OD=OE,
∴△BOD≌△COE,
∴∠B=∠C,∴AB=AC.
18.(1)∵PC是∠APB的平分线,
∴,当PC是圆的直径,
即∠PAC=90°时,四边形PACB面积最大,
在Rt△PAC中,∠APC=30°,AP=PB=AB=,
∴PC=2,
∴S四边形PACB=2S△ACP=PC·AB=×2×=.
(2)当∠PAC=120°时,四边形PACB是梯形,
∵PC是∠APB的平分线,∴∠APC=∠BPC=∠CAB=30°,
∴∠APB=60°,∴∠PAC+∠APB=180°,
∴AC∥PB.且AP与BC不平行,
∴四边形PACB是梯形,
当∠PAC=60°时,四边形PACB是梯形,
∵,∴AC=BC,
又∵∠BAC=30°,∴∠ACB=120°,
∴∠PAC+∠ACB=180°,
∴BC∥AP且AC与PB不平行,
∴四边形PACB是梯形.
- 1 -
同课章节目录
