北师大版数学七年级上册 第四章 基本平面图形过关训练课件(共31张PPT)
文档属性
| 名称 | 北师大版数学七年级上册 第四章 基本平面图形过关训练课件(共31张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-08 00:00:00 | ||
图片预览



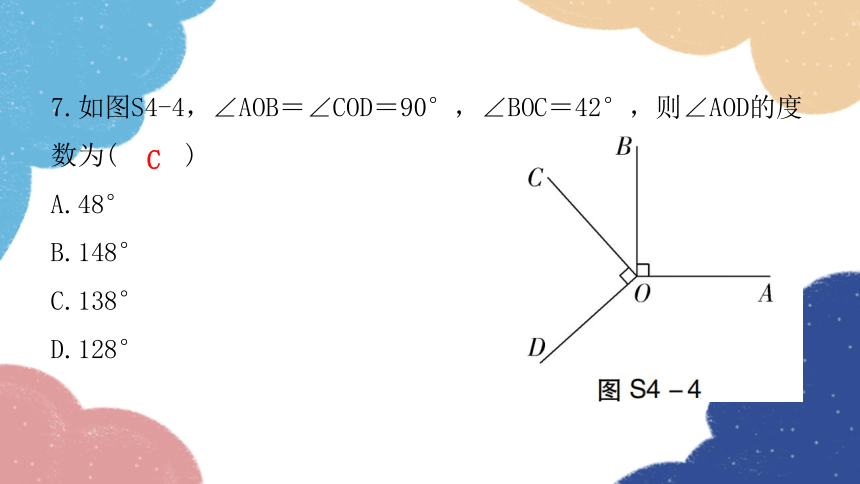



文档简介
(共31张PPT)
第四章 基本平面图形过关训练
过关训练+综合训练
一、选择题(本大题10小题,每小题3分,共30分)
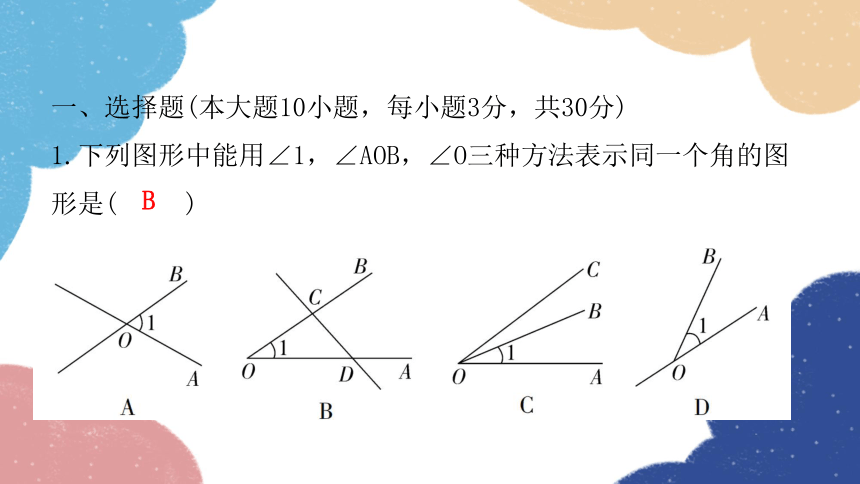
1.下列图形中能用∠1,∠AOB,∠O三种方法表示同一个角的图形是( )
B
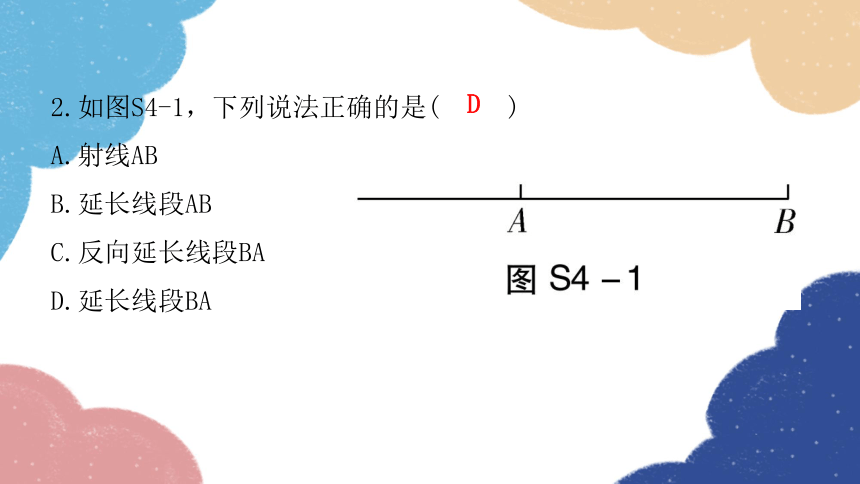
2.如图S4-1,下列说法正确的是( )
A.射线AB
B.延长线段AB
C.反向延长线段BA
D.延长线段BA
D
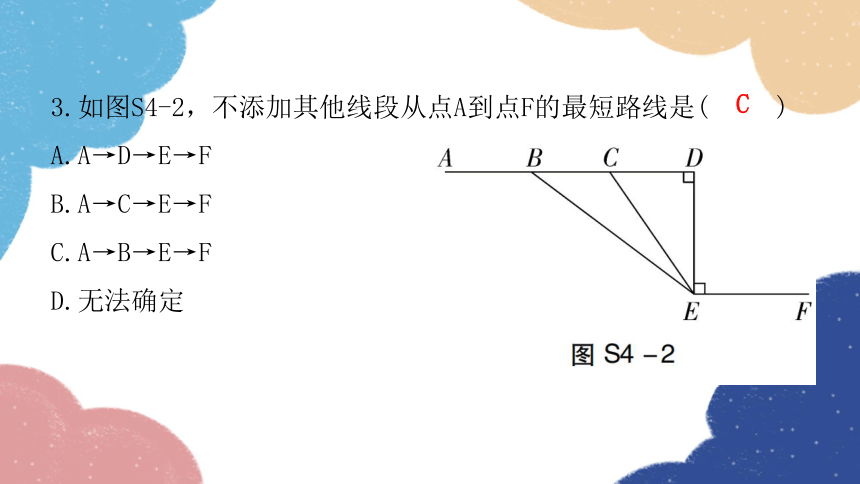
3.如图S4-2,不添加其他线段从点A到点F的最短路线是( )
A.A→D→E→F
B.A→C→E→F
C.A→B→E→F
D.无法确定
C
4.语句中正确的是( )
A.线段AB就是A,B两点间的距离
B.画射线AB=10 cm
C.A,B两点之间的所有连线中,线段AB最短
D.如果AB=BC,那么点A与点C重合
C
5.将31.24°化为度、分、秒的形式为( )
A.31°14′24″ B.31°16′24″
C.31°14′26″ D.31°16′26″
A
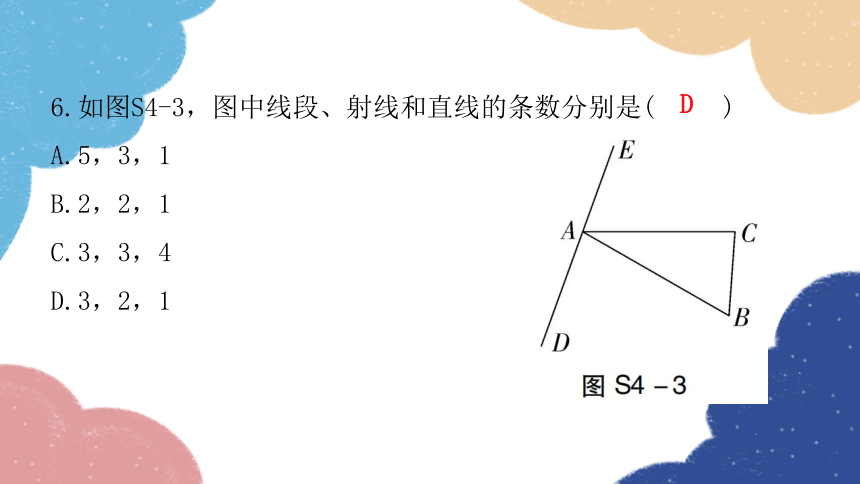
6.如图S4-3,图中线段、射线和直线的条数分别是( )
A.5,3,1
B.2,2,1
C.3,3,4
D.3,2,1
D
7.如图S4-4,∠AOB=∠COD=90°,∠BOC=42°,则∠AOD的度数为( )
A.48°
B.148°
C.138°
D.128°
C
8.如图S4-5,已知点A在点O的北偏东42°40′方向上,点B在点O的正南方向,OE平分∠AOB,则点E相对于点O的方位可表示为( )
A.南偏东68°40′方向
B.南偏东69°40′方向
C.南偏东68°20′方向
D.南偏东69°10′方向
A
D
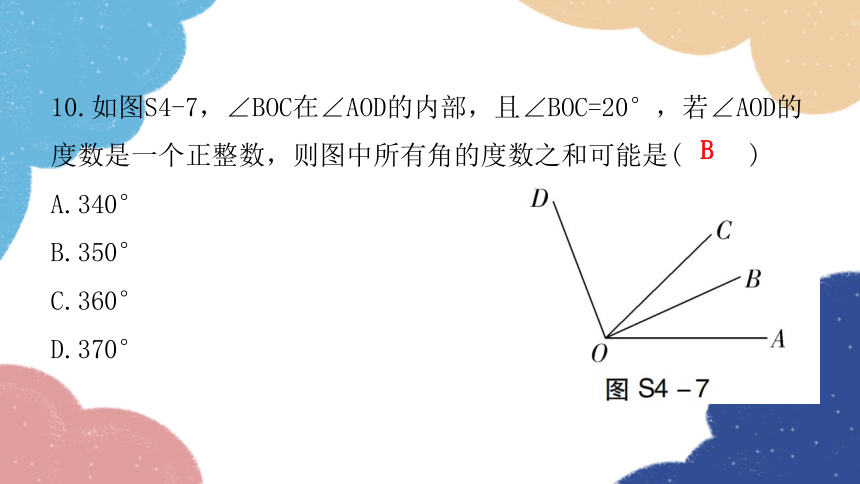
10.如图S4-7,∠BOC在∠AOD的内部,且∠BOC=20°,若∠AOD的度数是一个正整数,则图中所有角的度数之和可能是( )
A.340°
B.350°
C.360°
D.370°
B
二、填空题(本大题5小题,每小题3分,共15分)
11.高速公路的建设带动我国经济的快速发展.在高速公路的建设中,通常要从大山中开挖隧道穿过,把道路取直,以缩短路程.这样做蕴含的数学道理是_______________________.
12.某校下午放学的时间是4:30,此时时针与分针夹角的度数为________.
两点之间,线段最短
45°
13.将一个圆分成四个扇形,它们的圆心角的度数比为4∶4∶5∶7,则其中最大扇形的圆心角的度数是________.
14.如图S4-8,已知OE是∠AOC的平分线,
OD是∠BOC的平分线,若∠AOC=110°,
∠BOC=30°,则∠DOE=________°.
126°
40
15.已知∠AOC=2∠BOC,∠BOC=30°,
则∠AOB的度数为______________.
30°或90°
三、解答题(一)(本大题3小题,每小题8分,共24分)
16.如图S4-9,已知线段a,b,利用尺规作一条线段AB,使AB=a+3b.(保留作图痕迹,不写作法)
解:如答图S4-1,线段AB即为所求.
17.如图S4-10,直线AB,CD相交于点O,且∠DOE=3∠COE,∠EOB=90°,求∠AOD的度数.
解:因为∠DOE=3∠COE,∠DOE+∠COE=180°,
所以∠DOE=135°.
因为∠EOB=90°,
所以∠BOD=∠DOE-∠EOB=45°.
所以∠AOD=180°-∠BOD=135°.
四、解答题(二)(本大题3小题,每小题9分,共27分)
19.如图S4-12,已知O是直线AB上的一点,∠COD是直角,OE平分∠BOC.
(1)若∠AOC=30°,求∠DOE的度数;
(2)若∠AOC=α,求∠DOE的度数.(用
含α的代数式表示)
20.如图S4-13,已知线段AB=15 cm,CD=3 cm,E是AC的中点,F是BD的中点.
(1)若AC=4 cm,求线段EF的长;
(2)当线段CD在线段AB上从左向右或从右向左运动时,试判断线段EF的长是否发生变化?若不变,请求出线段EF的长度;若变化,请说明理由.
21.如图S4-14,已知轮船A在灯塔P的北偏东30°的方向上,轮船B在灯塔P的南偏东70°的方向上.
(1)求从灯塔P看两轮船的视角(即
∠APB)的度数;
(2)若轮船C在∠APB的平分线上,
则轮船C在灯塔P的什么方向上?
五、解答题(三)(本大题2小题,每小题12分,共24分)
22.点O为直线AB上一点,过点O作射线OC.将一直角三角板的直角顶点放在点O处.
(1)如图S4-15①,若∠BOC=65°,将三角板MON的一边ON与射线OB重合时,则∠MOC=________;
25°
(2)如图S4-15②,若∠BOC=65°,将三角板MON绕点O逆时针旋转一定角度,此时OC是∠MOB的平分线.
①∠BON=________;
②若∠BOC=α,求∠AOM的度数.
40°
解:(2)②因为OC是∠MOB的平分线,
所以∠BOM=2∠BOC=2α.
所以∠AOM=180°-∠BOM=180°-2α.
23.如图S4-16①,已知C,D是线段AB上两点,D是AC的中点,若CB=4 cm,DB=7 cm.
(1)求线段AB的长;
(2)如图S4-16②,若
M,N分别为AD,CB的
中点,求线段MN的长;
(3)类比以上探究,如图S4-16③,解决以下问题:射线OA,OB分别为∠MOP和∠NOP的平分线,∠MON=α,∠NOP=β(β<α).求∠AOB的大小.
解:(1)因为CB=4 cm,DB=7 cm.
所以DC=DB-CB=3(cm).
因为D是AC的中点,
所以AC=2DC=6(cm).
所以AB=AC+CB=10(cm).
谢 谢!
第四章 基本平面图形过关训练
过关训练+综合训练
一、选择题(本大题10小题,每小题3分,共30分)
1.下列图形中能用∠1,∠AOB,∠O三种方法表示同一个角的图形是( )
B
2.如图S4-1,下列说法正确的是( )
A.射线AB
B.延长线段AB
C.反向延长线段BA
D.延长线段BA
D
3.如图S4-2,不添加其他线段从点A到点F的最短路线是( )
A.A→D→E→F
B.A→C→E→F
C.A→B→E→F
D.无法确定
C
4.语句中正确的是( )
A.线段AB就是A,B两点间的距离
B.画射线AB=10 cm
C.A,B两点之间的所有连线中,线段AB最短
D.如果AB=BC,那么点A与点C重合
C
5.将31.24°化为度、分、秒的形式为( )
A.31°14′24″ B.31°16′24″
C.31°14′26″ D.31°16′26″
A
6.如图S4-3,图中线段、射线和直线的条数分别是( )
A.5,3,1
B.2,2,1
C.3,3,4
D.3,2,1
D
7.如图S4-4,∠AOB=∠COD=90°,∠BOC=42°,则∠AOD的度数为( )
A.48°
B.148°
C.138°
D.128°
C
8.如图S4-5,已知点A在点O的北偏东42°40′方向上,点B在点O的正南方向,OE平分∠AOB,则点E相对于点O的方位可表示为( )
A.南偏东68°40′方向
B.南偏东69°40′方向
C.南偏东68°20′方向
D.南偏东69°10′方向
A
D
10.如图S4-7,∠BOC在∠AOD的内部,且∠BOC=20°,若∠AOD的度数是一个正整数,则图中所有角的度数之和可能是( )
A.340°
B.350°
C.360°
D.370°
B
二、填空题(本大题5小题,每小题3分,共15分)
11.高速公路的建设带动我国经济的快速发展.在高速公路的建设中,通常要从大山中开挖隧道穿过,把道路取直,以缩短路程.这样做蕴含的数学道理是_______________________.
12.某校下午放学的时间是4:30,此时时针与分针夹角的度数为________.
两点之间,线段最短
45°
13.将一个圆分成四个扇形,它们的圆心角的度数比为4∶4∶5∶7,则其中最大扇形的圆心角的度数是________.
14.如图S4-8,已知OE是∠AOC的平分线,
OD是∠BOC的平分线,若∠AOC=110°,
∠BOC=30°,则∠DOE=________°.
126°
40
15.已知∠AOC=2∠BOC,∠BOC=30°,
则∠AOB的度数为______________.
30°或90°
三、解答题(一)(本大题3小题,每小题8分,共24分)
16.如图S4-9,已知线段a,b,利用尺规作一条线段AB,使AB=a+3b.(保留作图痕迹,不写作法)
解:如答图S4-1,线段AB即为所求.
17.如图S4-10,直线AB,CD相交于点O,且∠DOE=3∠COE,∠EOB=90°,求∠AOD的度数.
解:因为∠DOE=3∠COE,∠DOE+∠COE=180°,
所以∠DOE=135°.
因为∠EOB=90°,
所以∠BOD=∠DOE-∠EOB=45°.
所以∠AOD=180°-∠BOD=135°.
四、解答题(二)(本大题3小题,每小题9分,共27分)
19.如图S4-12,已知O是直线AB上的一点,∠COD是直角,OE平分∠BOC.
(1)若∠AOC=30°,求∠DOE的度数;
(2)若∠AOC=α,求∠DOE的度数.(用
含α的代数式表示)
20.如图S4-13,已知线段AB=15 cm,CD=3 cm,E是AC的中点,F是BD的中点.
(1)若AC=4 cm,求线段EF的长;
(2)当线段CD在线段AB上从左向右或从右向左运动时,试判断线段EF的长是否发生变化?若不变,请求出线段EF的长度;若变化,请说明理由.
21.如图S4-14,已知轮船A在灯塔P的北偏东30°的方向上,轮船B在灯塔P的南偏东70°的方向上.
(1)求从灯塔P看两轮船的视角(即
∠APB)的度数;
(2)若轮船C在∠APB的平分线上,
则轮船C在灯塔P的什么方向上?
五、解答题(三)(本大题2小题,每小题12分,共24分)
22.点O为直线AB上一点,过点O作射线OC.将一直角三角板的直角顶点放在点O处.
(1)如图S4-15①,若∠BOC=65°,将三角板MON的一边ON与射线OB重合时,则∠MOC=________;
25°
(2)如图S4-15②,若∠BOC=65°,将三角板MON绕点O逆时针旋转一定角度,此时OC是∠MOB的平分线.
①∠BON=________;
②若∠BOC=α,求∠AOM的度数.
40°
解:(2)②因为OC是∠MOB的平分线,
所以∠BOM=2∠BOC=2α.
所以∠AOM=180°-∠BOM=180°-2α.
23.如图S4-16①,已知C,D是线段AB上两点,D是AC的中点,若CB=4 cm,DB=7 cm.
(1)求线段AB的长;
(2)如图S4-16②,若
M,N分别为AD,CB的
中点,求线段MN的长;
(3)类比以上探究,如图S4-16③,解决以下问题:射线OA,OB分别为∠MOP和∠NOP的平分线,∠MON=α,∠NOP=β(β<α).求∠AOB的大小.
解:(1)因为CB=4 cm,DB=7 cm.
所以DC=DB-CB=3(cm).
因为D是AC的中点,
所以AC=2DC=6(cm).
所以AB=AC+CB=10(cm).
谢 谢!
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
