24.2.2直线与圆的位置关系(4)—三角形内切圆[上学期]
文档属性
| 名称 | 24.2.2直线与圆的位置关系(4)—三角形内切圆[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 232.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-10-07 20:56:00 | ||
图片预览


文档简介
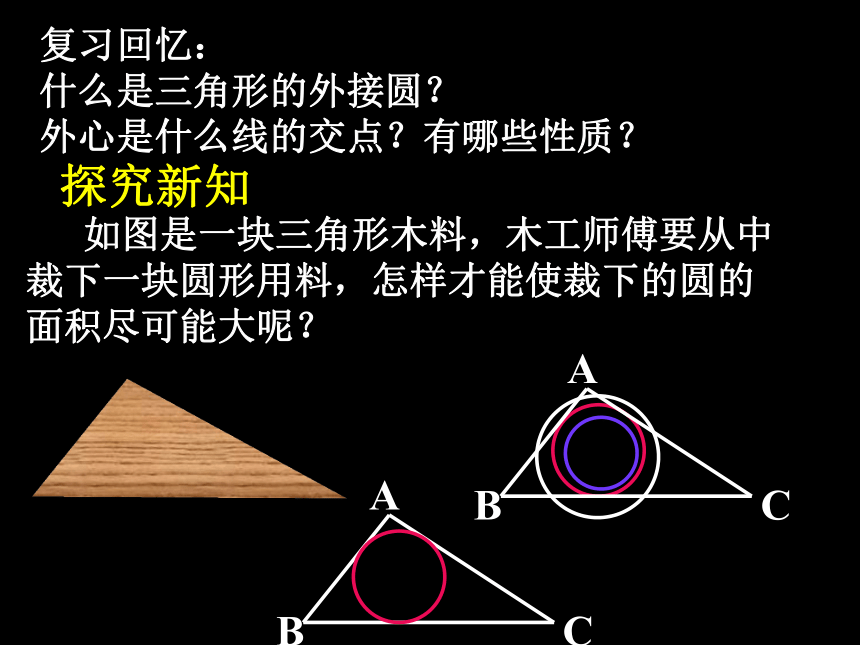
课件16张PPT。 24.2.2三角形的内切圆探究新知复习回忆:
什么是三角形的外接圆?
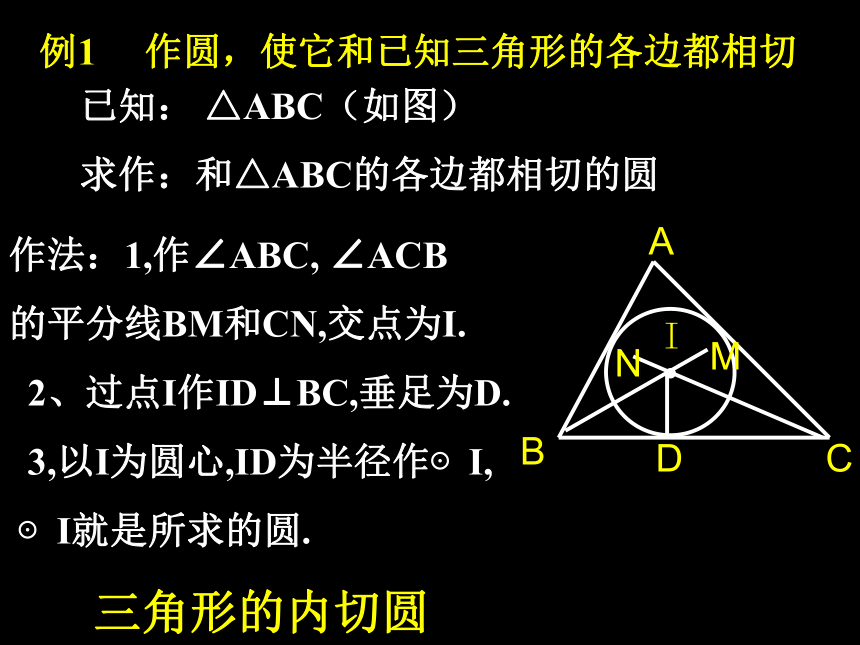
外心是什么线的交点?有哪些性质? 例1 作圆,使它和已知三角形的各边都相切已知: △ABC(如图)
求作:和△ABC的各边都相切的圆作法:1,作∠ABC, ∠ACB
的平分线BM和CN,交点为I.
2、过点I作ID⊥BC,垂足为D.
3,以I为圆心,ID为半径作⊙I,
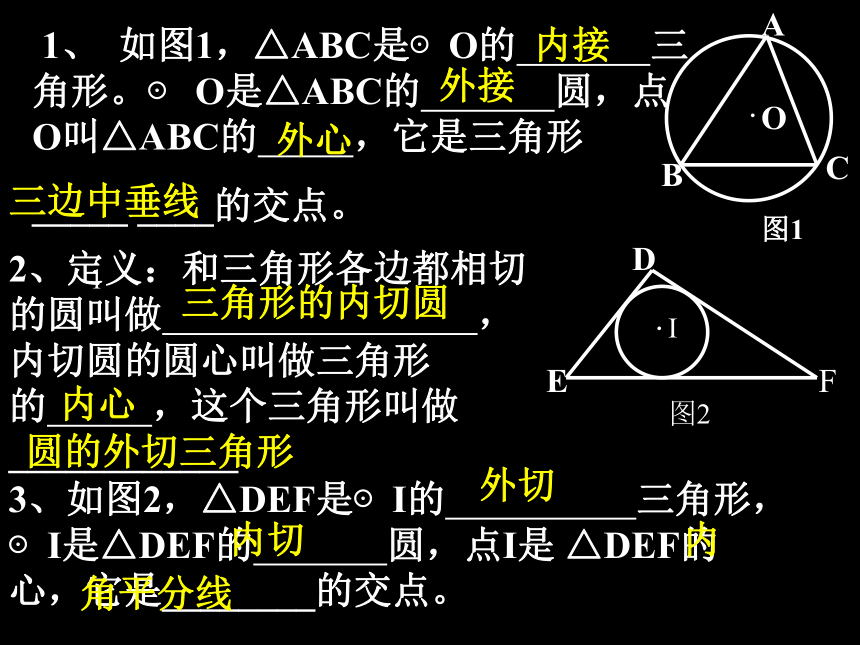
⊙I就是所求的圆.CBMIAND三角形的内切圆 1、 如图1,△ABC是⊙O的 三角形。⊙ O是△ABC的 圆,点O叫△ABC的 ,它是三角形
_____ ____的交点。外接内接外心三边中垂线13、如图2,△DEF是⊙I的 三角形, ⊙I是△DEF的 圆,点I是 △DEF的 心,它是________的交点。2、定义:和三角形各边都相切的圆叫做 ,内切圆的圆心叫做三角形的 ,这个三角形叫做____________ 三角形的内切圆内心圆的外切三角形外切内切内角平分线三角形内心的性质:1、三角形的内心到三角形各边的距离相等;
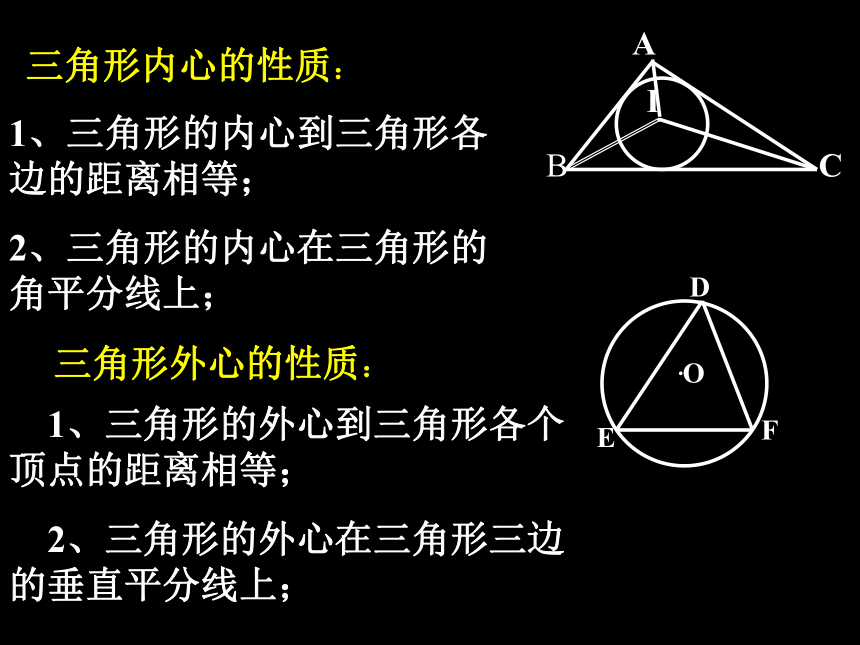
2、三角形的内心在三角形的 角平分线上; 1、三角形的外心到三角形各个 顶点的距离相等;
2、三角形的外心在三角形三边 的垂直平分线上; 三角形外心的性质:定义:和多边形各边都相切的圆叫做 ,这个多边形叫做 。 多边形的内切 圆圆的外切多边形内切外切如上图,四边形DEFG是⊙O的 四
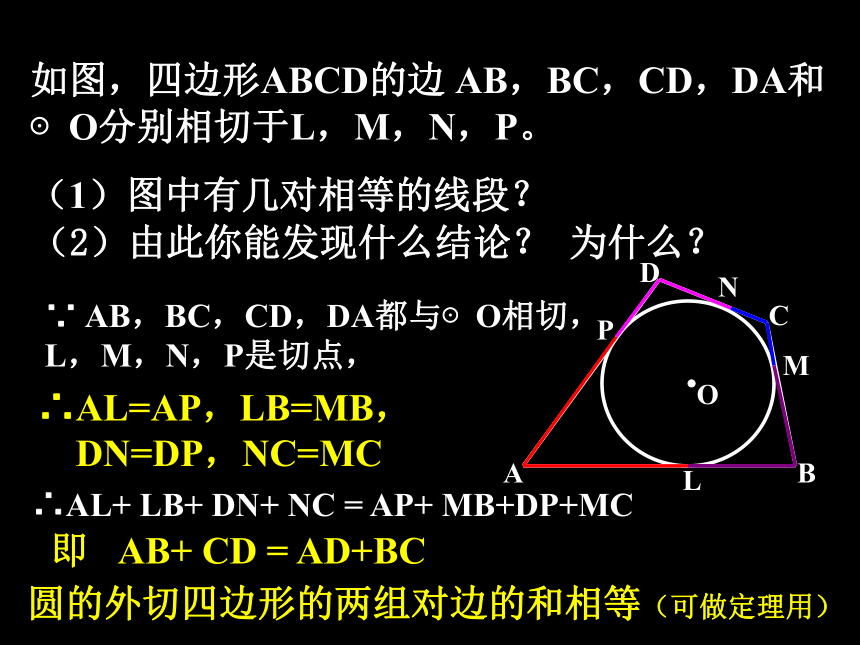
边形,⊙O是四边形DEFG的 圆,再探究新知如图,四边形ABCD的边 AB,BC,CD,DA和⊙O分别相切于L,M,N,P。
(1)图中有几对相等的线段?(2)由此你能发现什么结论? 为什么?∵ AB,BC,CD,DA都与⊙O相切,
L,M,N,P是切点,∴AL=AP,LB=MB,
DN=DP,NC=MC∴AL+ LB+ DN+ NC = AP+ MB+DP+MC即 AB+ CD = AD+BC圆的外切四边形的两组对边的和相等(可做定理用)定理:圆的外切四边形的两组对边和相等。比较圆的内接四边形的性质:8cm6cm4cm6cm等腰梯形各边都与⊙O相切, ⊙O的直径为6cm,等腰梯形的腰等于8cm,则梯形的面积为_____。868 判断题:
1、三角形的内心到三角形各个顶点的距离相等
2、三角形的外心到三角形各边的距离相等 ( )
3、等边三角形的内心和外心重合; ( )
4、三角形的内心一定在三角形的内部( )
5、菱形一定有内切圆( )
6、矩形一定有内切圆( )
错错对对 错 对例2已知:△ABC是⊙O外切三角形,切点为D,E,F,若BC=14 cm ,AC=9cm,AB=13cm.求AF,BD,CE。解:设AF=Xcm, BD=Ycm,CE=Zcm则AE=AF=Xcm ,DC=BD=Ycm, AE=EC=Zcm依题意得方程组
例3 如图,在△ABC中,点O是内心, (1)若∠ABC=50°, ∠ACB=70°,求∠BOC的度数(2)若∠A=80 °,则∠BOC= 度。
(3)若∠BOC=100 °,则∠A= 度。
解(1)∵点O是△ABC的内心,
∴ ∠OBC= ∠OBA= ∠ABC= 25 °
同理 ∠OCB= ∠OCA= ∠ACB=35 °13020∴ ∠BOC=180 °- (∠OBC+ ∠OCB)
= 180 -60 °=120 ° O是内心,∠A与∠BOC之间存在怎样的数量关系?请说明理由。理由: ∵点O是△ABC的内心, 答: ∠BOC =90 ° + ∠A∴ ∠OBC= ∠ABC, ∠OCB= ∠ACB∴ ∠OBC+ ∠OCB = (∠ABC+ ∠ACB)= (180 - ∠A )= 90 °- ∠A∴ ∠BOC =180 °-( ∠OBC+ ∠OCB )= 180 -( 90 - ∠A )= 90 + ∠A三探究新知 ⊿ABC 中,AB= 50,BC=40,AC=30,
求三角形内切圆的半径0BDEACF设O是△ABC的内心, ⊙O的半径为r米,
连结AO、BO、CO,
⊙O分别切AC、BC、AB于点D、E、F,则MD⊥AC, OE ⊥BC, OF ⊥AB,
则OD= OE= OF=r,
∵AC=30,BC=40, AB=50
∴AD=AF=30-r,BE=BF=40-r
∵ AB=AF+BF
∴ (30+r)+(40-r)=50
∴已知:如图,⊙O是Rt△ABC的内切圆,∠C是直角,三边长分别是a,b,c.
求⊙O的半径r.
Rt△的三边长与其内切圆半径间的关系练习:直角三角形的两直角边分别是5cm,
12cm 则其内切圆的半径为______。 谈谈你的收获------------
1、三角形内切圆的作法 .
2,类比三角形的外接圆与圆的内接三角形概念与三角形的内切圆,圆的外切三角形概念.要明确“接”和“切”的含义,,弄清“内心”与“外心”的区别,
3.直角三角形内切圆半径的公式,以及圆的外切四边形的性质.
什么是三角形的外接圆?
外心是什么线的交点?有哪些性质? 例1 作圆,使它和已知三角形的各边都相切已知: △ABC(如图)
求作:和△ABC的各边都相切的圆作法:1,作∠ABC, ∠ACB
的平分线BM和CN,交点为I.
2、过点I作ID⊥BC,垂足为D.
3,以I为圆心,ID为半径作⊙I,
⊙I就是所求的圆.CBMIAND三角形的内切圆 1、 如图1,△ABC是⊙O的 三角形。⊙ O是△ABC的 圆,点O叫△ABC的 ,它是三角形
_____ ____的交点。外接内接外心三边中垂线13、如图2,△DEF是⊙I的 三角形, ⊙I是△DEF的 圆,点I是 △DEF的 心,它是________的交点。2、定义:和三角形各边都相切的圆叫做 ,内切圆的圆心叫做三角形的 ,这个三角形叫做____________ 三角形的内切圆内心圆的外切三角形外切内切内角平分线三角形内心的性质:1、三角形的内心到三角形各边的距离相等;
2、三角形的内心在三角形的 角平分线上; 1、三角形的外心到三角形各个 顶点的距离相等;
2、三角形的外心在三角形三边 的垂直平分线上; 三角形外心的性质:定义:和多边形各边都相切的圆叫做 ,这个多边形叫做 。 多边形的内切 圆圆的外切多边形内切外切如上图,四边形DEFG是⊙O的 四
边形,⊙O是四边形DEFG的 圆,再探究新知如图,四边形ABCD的边 AB,BC,CD,DA和⊙O分别相切于L,M,N,P。
(1)图中有几对相等的线段?(2)由此你能发现什么结论? 为什么?∵ AB,BC,CD,DA都与⊙O相切,
L,M,N,P是切点,∴AL=AP,LB=MB,
DN=DP,NC=MC∴AL+ LB+ DN+ NC = AP+ MB+DP+MC即 AB+ CD = AD+BC圆的外切四边形的两组对边的和相等(可做定理用)定理:圆的外切四边形的两组对边和相等。比较圆的内接四边形的性质:8cm6cm4cm6cm等腰梯形各边都与⊙O相切, ⊙O的直径为6cm,等腰梯形的腰等于8cm,则梯形的面积为_____。868 判断题:
1、三角形的内心到三角形各个顶点的距离相等
2、三角形的外心到三角形各边的距离相等 ( )
3、等边三角形的内心和外心重合; ( )
4、三角形的内心一定在三角形的内部( )
5、菱形一定有内切圆( )
6、矩形一定有内切圆( )
错错对对 错 对例2已知:△ABC是⊙O外切三角形,切点为D,E,F,若BC=14 cm ,AC=9cm,AB=13cm.求AF,BD,CE。解:设AF=Xcm, BD=Ycm,CE=Zcm则AE=AF=Xcm ,DC=BD=Ycm, AE=EC=Zcm依题意得方程组
例3 如图,在△ABC中,点O是内心, (1)若∠ABC=50°, ∠ACB=70°,求∠BOC的度数(2)若∠A=80 °,则∠BOC= 度。
(3)若∠BOC=100 °,则∠A= 度。
解(1)∵点O是△ABC的内心,
∴ ∠OBC= ∠OBA= ∠ABC= 25 °
同理 ∠OCB= ∠OCA= ∠ACB=35 °13020∴ ∠BOC=180 °- (∠OBC+ ∠OCB)
= 180 -60 °=120 ° O是内心,∠A与∠BOC之间存在怎样的数量关系?请说明理由。理由: ∵点O是△ABC的内心, 答: ∠BOC =90 ° + ∠A∴ ∠OBC= ∠ABC, ∠OCB= ∠ACB∴ ∠OBC+ ∠OCB = (∠ABC+ ∠ACB)= (180 - ∠A )= 90 °- ∠A∴ ∠BOC =180 °-( ∠OBC+ ∠OCB )= 180 -( 90 - ∠A )= 90 + ∠A三探究新知 ⊿ABC 中,AB= 50,BC=40,AC=30,
求三角形内切圆的半径0BDEACF设O是△ABC的内心, ⊙O的半径为r米,
连结AO、BO、CO,
⊙O分别切AC、BC、AB于点D、E、F,则MD⊥AC, OE ⊥BC, OF ⊥AB,
则OD= OE= OF=r,
∵AC=30,BC=40, AB=50
∴AD=AF=30-r,BE=BF=40-r
∵ AB=AF+BF
∴ (30+r)+(40-r)=50
∴已知:如图,⊙O是Rt△ABC的内切圆,∠C是直角,三边长分别是a,b,c.
求⊙O的半径r.
Rt△的三边长与其内切圆半径间的关系练习:直角三角形的两直角边分别是5cm,
12cm 则其内切圆的半径为______。 谈谈你的收获------------
1、三角形内切圆的作法 .
2,类比三角形的外接圆与圆的内接三角形概念与三角形的内切圆,圆的外切三角形概念.要明确“接”和“切”的含义,,弄清“内心”与“外心”的区别,
3.直角三角形内切圆半径的公式,以及圆的外切四边形的性质.
同课章节目录
