1.3.1单调性与最大(小)值(三)
文档属性
| 名称 | 1.3.1单调性与最大(小)值(三) |  | |
| 格式 | zip | ||
| 文件大小 | 609.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-12-01 19:10:48 | ||
图片预览









文档简介
课件51张PPT。(三)1.3.1单调性与最大(小)值
【教学重点】【教学目标】【教学难点】课程目标理解增函数、减函数的概念掌握判断某些函数增减性的方法步渗透数形结合的数学方法函数单调性概念的理解及应用函数单调性的判定及证明教法:自学辅导法、讨论法、讲授法学法:归纳—讨论—练习【教学方法】【教学手段】多媒体电脑与投影仪?判断函数 在区间(-1,1)上的单调性.解:设则 f(x1)-f(x2)∵-1<x1<x2<1,∴1+x1x2>0,x2-x1>0,∴ f(x1)-f(x2)>0 .即 f(x1)>f(x2) .故此函数在(-1,1)上是减函数.课前热身利用函数单调性判断函数的最大(小)值的方法 1.利用二次函数的性质(配方法)求函数的最大(小)值 2. 利用图象求函数的最大(小)值 3.利用函数单调性的判断函数的最大(小)值 如果函数y=f(x)在区间[a,b]上单调递增,则函数y=f(x)在x=a处有最小值f(a),在x=b处有最大值f(b) ; 如果函数y=f(x)在区间[a,b]上单调递减,在区间[b,c]上单调递增则函数y=f(x)在x=b处有最小值f(b); 1.增函数与减函数 一般地,设函数y=f(x)的定义域为I,如果对于定义域I内的某个区间D内的任意两个自变量x1,x2,当x1(2)作差f(x1)-f(x2);
(3)变形;
(4)判号(即判断差f(x1)-f(x2)的正负);
(5)定论(即指出函数f(x)在给定的区间D上的单调性).3.利用单调性定义证明函数f(x)在给定的区间D上的单调性的一般步骤:4.常见函数的单调性:在
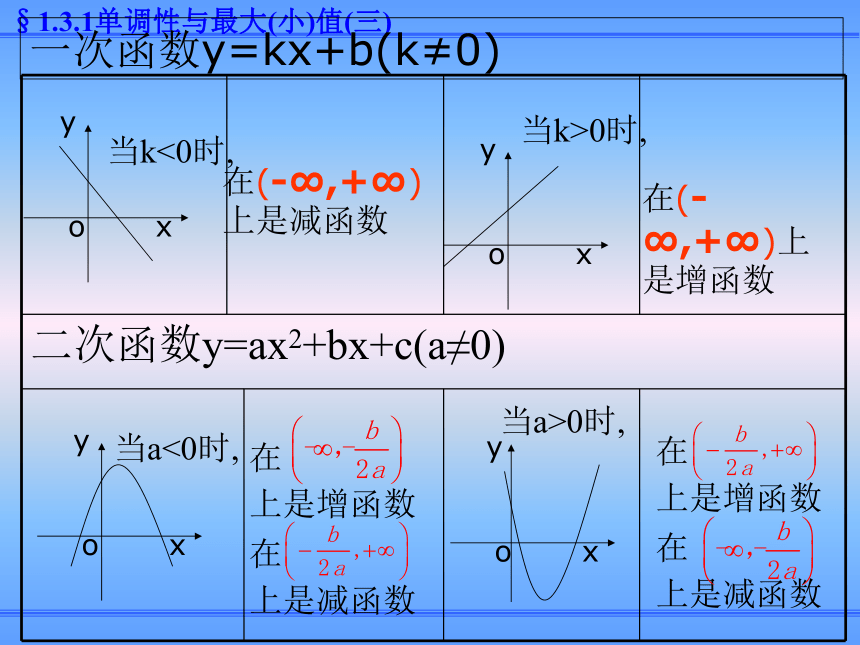
上是增函数
在
上是减函数在
上是增函数
在
上是减函数在(-∞,+∞)上是减函数
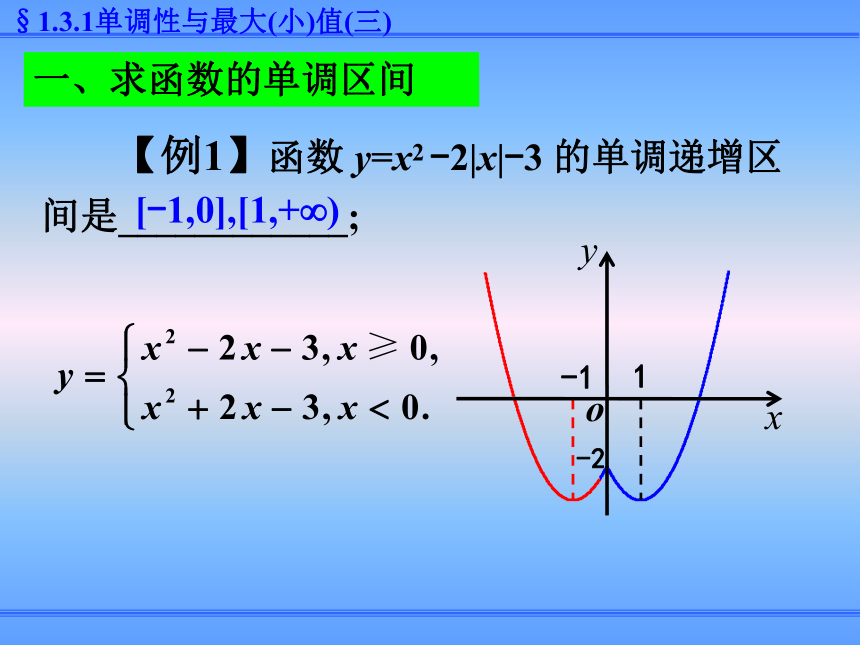
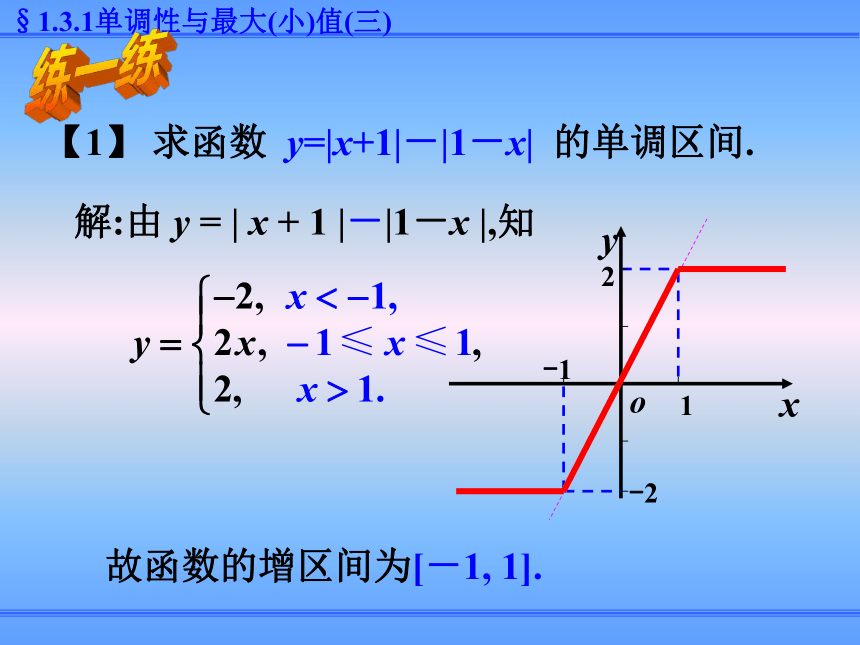
在(-∞,+∞)上是增函数一次函数y=kx+b(k≠0)1.利用二次函数的性质(配方法)求函数的最 大(小)值 2. 利用图象求函数的最大(小)值 3.利用函数单调性的判断函数的最大(小)值 如果函数y=f(x)在区间[a,b]上单调递增,则函数y=f(x)在x=a处有最小值f(a),在x=b处有最大值f(b); 如果函数y=f(x)在区间[a,b]上单调递减,在区间[b,c]上单调递增则函数y=f(x)在x=b处有最小值f(b).利用函数单调性判断函数的最大(小)值的方法1.求函数的单调区间;2.判断函数的单调性(证明);5.求函数的最值或值域3.比较函数的大小函数单调性的应用4.求参数的取值范围 【例1】函数 y=x2 -2|x|-3 的单调递增区间是____________;[-1,0],[1,+?)-21-1一、求函数的单调区间【1】 求函数 y=|x+1|-|1-x| 的单调区间.解:由 y = | x + 1 |-|1-x |,知故函数的增区间为[-1, 1].练一练【2】画出函数y = |x2-2x-3|的图象.解:当 x2-2x-3≥0 ,即 x ≤-1 或 x≥3 时,y = x2-2x-3=( x-1)2-4. 当 x2-2x-3<0, 即 -1<x<3时,y =-(x2-2x-3) =-(x-1)2+4. 【3】求函数y=2|x-1|-3|x|的最大值.解:(1)当x<0时,y=-2(x-1)+3x=x+2;(2)当0≤x<1时,y=-2(x-1)-3x=-5x+2;(3)当x≥1时,y=2(x-1)+3x=-x-2.备课资料1.函数 的单调减区间为______.2.函数y=|2x-1|的单调增区间是______.巩固练习【例2】证明函数 在 上是减函数.二、判断(证明)函数的单调性证明:任取因此 在 上是减函数.【例2】证明函数 在二、判断(证明)函数的单调性上是减函数.另解:向上平移向左平移2 个单位3个单位所以函数f(x)的递减区间是 练一练【1】写出函数 的单调区间. 例3.已知函数 对任意实数t都有 比较f(1), f(2), f(3)的大小.三、利用单调性比较函数值的大小 【1】已知函数f(x)在(0,+∞)上是减函数,则
的大小关系为___________. 练一练1.设函数y=x2+2(a-1)x+2在区间[2,+?)上是增函数,求实数a的取值范围.解:函数y=x2+2(a-1)x+2的对称轴方程为x=1-a,函数的单调增区间是[1-a,+?),∴ [2,+?)是[1-a,+?)的一个子集,∴ 1-a≤2即a≥-1.即所求的实数取值范围是a≥-1.图象演示由二次函数性质知,四、利用函数单调性求参数的取值范围 【1】函数f(x)=x2+4ax+2在区间(-∞,6]内递减,则a的取值范围是………………( )
A.a≥3 B.a≤3
C.a≥-3 D.a≤-3D 【2】在已知函数f(x)=4x2-mx+1,在(-∞,-2]上递减,在[-2,+∞)上递增,则f(x)在[1,2]上的值域________.[21,39]练一练 【3】已知f(x)是R上的增函数, 若a+b>0,则有f(a)+f(b)>f(-a)+f(-b).证明:由a+b>0,得a>-b,b>-a.又因为f(x)是R上的增函数,∴ f(a) > f(-b), ① f(b)>f(-a), ②①+②得f(a)+f(b) >f(-a)+f(-b).练一练分析:设则确定 正负号的关键,是确定的正负号.由于x1, x2在同一区间内,要使 则需要使 则需例5.求函数 的最大值.五、求函数的最大(小)值或值域例5.求函数 的最大值.解:任取x1, x2 , x1, x2∈[2,4],且x1< x2,当 时,所以函数f(x)在[2,4]上是减函数.同理函数f(x)在[4,10]上是增函数.五、求函数的最大(小)值或值域解:∵函数在[2,4]上是减函数.所以f(x)在[2,4]上有最大值,∵函数在[4,10]上是增函数.所以f(x)在[4,10]上有最大值,所以函数f(x)在[2,10]上的最大值是几何画板 例6.函数f(x)是定义在(0,+?)上的递减函数,且f(x)< f(2x-3),求x的取值范围.解: ∵函数f(x) 在(0,+?)上为减函数,∴x的取值范围是.解之, 得模拟试验六、利用函数单调性解不等式 【1】已知函数y=f(x)在定义域R上是单调减函数,且f(a+1) > f(3-a),求实数a 的取值范围 【2】函数y=f(x)是定义在(-1,1)上的减函数,若f(2-a) > f(3-a),求实数a 的取值范围练一练【例3】求f(x)=x2-2ax+2在 [ 2,4 ]上的最小值.解:f (x) = (x-a) 2+2-a 2,① 当a<2时,②当2≤a<4 时, ③当a≥4时, ∴ f(x)min=f(2)=6-4a;f(x)在[ 2,4 ]上是增函数,∴ f(x)min=f(a)=2-a2.f(x)在[2,4]上是减函数.∴ f(x)min=f(4) = 18-8a.几何画板七、有关最值讨论题求最大值:① 当 a < 3 时, ② 当 a ≥ 3 时, f ( x ) max = f ( x ) max = f ( 4 ) = 18 -8af ( x ) max = f ( 2 ) = 6 -4a例6.已知f(x)=x2-4x-4,x∈[t,t+1](t∈R ),
求 f(x)的最小值g(t)的解析式.解:f(x)=(x-2)2-8(1)当2∈[t,t+2],即1≤t≤2时, g(t)=f(2)=-8;(2) 当 t > 2 时,∴g(t) = f(t)=t2-4t-4;(3)当t+1<2,即t<1时,f(x)在[t,t+1]上是减函数,∴g(t)=f(t+1)=t2-2t -7.综上所述:g ( t ) = f(x)在[t,t+1]上是增函数,教材P11 练习T4.教材P12 A组T7,9,10.作业布置再见2007年9月13日山东省临沂一中 李福国课堂小结1.函数单调性的定义:图象法定义法2.函数单调性的判定:3.函数单调性的应用:(1)设元:对任意x1,x2∈D,且x1<x2
(2)作差:f(x1)-f(x2)
(3)变形
(4)判号
(5)定论
*求函数 的单调区间. 若函数f(x),g(x)在给定的区间I上具有单调性,
(1)k>0时,函数y=f(x)与y=kf(x)+b具有相同的单调性;
(2)若f(x)恒为正或恒为负时,函数f(x)与1/f(x)具有相反的单调性.
(3)若函数f(x),g(x)都是增(减)函数,则f(x)+g(x)仍是增(减)函数.
(4)若f(x)>0,g(x)>0,且f(x)与g(x)都是增(减)函数,则f(x)·g(x)也是增(减)函数;若f(x)<0,g(x)<0,且f(x)与g(x)都是增(减)函数,则f(x)·g(x)是减(增)函数.单调性性质规律总结:(4)奇函数在对称的区间上有相同的单调性,偶函数在对称的区间上有相反的单调性.
(5)复合函数f[g(x)]的单调性由f(x)和g(x)的单调性共同决定(同则增异则减) .单调性性质规律总结:复合函数:y=f[g(x)]令 u=g(x)则 y=f(u)内函数外函数y=f[g(x)]原函数以x为自变量以u为自变量以x为自变量(5)复合函数的单调性复合函数单调性结论: ①当内外函数在各自定义域内同增同减时,原函数增; ②当内外函数在各自定义域内一增一减时,原函数减. (1)f(x)是[a,b]上增函数,若存在x1, x2∈[a,b]且x1 (2)若存在x1, x2∈[a,b]且x1 (3)函数f(x)在[a,b]上满足f(a) < f(b),则f(x)在[a,b]上是增函数.
(4)若存在x1, x2∈[a,b]且x1f(x2) f(x)是[a,b]上减函数 .(正确)(错误)(错误)(错误)【2】判断下列两个命题的正误:练一练练习:注意:在原函数定义域内讨论函数的单调性补充练习: (1)f(x)是[a,b]上增函数,若存在x1, x2∈[a,b]且x1 (2)若存在x1, x2∈[a,b]且x1 (3)函数f(x)在[a,b]上满足f(a) < f(b),则f(x)在[a,b]上是增函数.
(4)若存在x1, x2∈[a,b]且x1f(x2) f(x)是[a,b]上减函数 .(正确)(错误)(错误)(错误)【1】判断下列说法是否正确.练一练①定义在R上的函数f(x)满足f(2)>f(1),则函数f(x)是R上的增函数( ).②定义在R上的函数f(x)满足f(2)>f(1),则函数f(x)在R上不是减函数( ).③函数y=f(x)在区间I上对于任意的x1,x2满足 ,则f(x)在区间I上为单调增函数( ). √√X练一练【2】判断下列说法是否正确.⑤定义在R上的函数f(x)在区间(-∞,0]上是增函数,在区间(0,+∞)上也是增函数,则函数f(x)在R上是增函数( ).⑥定义在R上的函数f(x)在区间(-∞,0]上是增函数,在区间[0,+∞)上也是增函数,则函数f(x)在R上是增函数( ).y√X④函数y=f(x)在区间I上对于任意的x1,x2 ,且x1① f(xy)=f(x)+f(y), ② f(2)=1, ③ 当 x>1 时, f(x)>0. (1)求证: f(x)为偶函数;(2)讨论函数的单调性;(3)求不等式 f(x)+f(x-3)≤2的解集.(1)证: 在①中令 x=y=1, 得 f(1)=f(1)+f(1) ?f(1)=0. 令 x=y=-1, 得 f(1)=f(-1)+f(-1)?f(-1)=0. 再令 y=-1, 得 f(-x)=f(x)+f(-1)=f(x). ∴f(x) 为偶函数. 先讨论 f(x) 在 (0, +∞) 上的单调性, 任取x1, x2, 设x2>x1>0, ∴f(x2)>f(x1). ∴f(x) 在 (0, +∞) 上是增函数, ∴由 (1) 知, f(x) 在(-∞, 0) 上是减函数. ∵偶函数图象关于 y 轴对称, (3)解: ∵f[x(x-3)]=f(x)+f(x-3)≤2, 由 ①、② 得 2=1+1=f(2)+f(2)=f(4)=f(-4), 1)若 x(x-3)>0, ∵ f(x) 在 (0, +∞) 上为增函数, ∴由 f[x(x-3)]≤f(4) 得: 2)若 x(x-3)<0, ∵ f(x) 在 (-∞, 0) 上为减函数, ∴由 f[x(x-3)]≤f(-4) 得: ∴原不等式的解集为[-1, 0)∪(0, 3)∪(3, 4]. 注 抽象函数问题是函数学习中一类比较特殊的问题, 其基本方法是变量代换、换元等, 应熟练掌握它们的这些特点. 法二 原不等式等价于 f[|x(x-3)|]≤f(4)(x?0, x-3?0), 由 f(x) 在 (0, +∞) 上为增函数得: |x(x-3)|≤4. 再进一步求得解集.
【教学重点】【教学目标】【教学难点】课程目标理解增函数、减函数的概念掌握判断某些函数增减性的方法步渗透数形结合的数学方法函数单调性概念的理解及应用函数单调性的判定及证明教法:自学辅导法、讨论法、讲授法学法:归纳—讨论—练习【教学方法】【教学手段】多媒体电脑与投影仪?判断函数 在区间(-1,1)上的单调性.解:设则 f(x1)-f(x2)∵-1<x1<x2<1,∴1+x1x2>0,x2-x1>0,∴ f(x1)-f(x2)>0 .即 f(x1)>f(x2) .故此函数在(-1,1)上是减函数.课前热身利用函数单调性判断函数的最大(小)值的方法 1.利用二次函数的性质(配方法)求函数的最大(小)值 2. 利用图象求函数的最大(小)值 3.利用函数单调性的判断函数的最大(小)值 如果函数y=f(x)在区间[a,b]上单调递增,则函数y=f(x)在x=a处有最小值f(a),在x=b处有最大值f(b) ; 如果函数y=f(x)在区间[a,b]上单调递减,在区间[b,c]上单调递增则函数y=f(x)在x=b处有最小值f(b); 1.增函数与减函数 一般地,设函数y=f(x)的定义域为I,如果对于定义域I内的某个区间D内的任意两个自变量x1,x2,当x1
(3)变形;
(4)判号(即判断差f(x1)-f(x2)的正负);
(5)定论(即指出函数f(x)在给定的区间D上的单调性).3.利用单调性定义证明函数f(x)在给定的区间D上的单调性的一般步骤:4.常见函数的单调性:在
上是增函数
在
上是减函数在
上是增函数
在
上是减函数在(-∞,+∞)上是减函数
在(-∞,+∞)上是增函数一次函数y=kx+b(k≠0)1.利用二次函数的性质(配方法)求函数的最 大(小)值 2. 利用图象求函数的最大(小)值 3.利用函数单调性的判断函数的最大(小)值 如果函数y=f(x)在区间[a,b]上单调递增,则函数y=f(x)在x=a处有最小值f(a),在x=b处有最大值f(b); 如果函数y=f(x)在区间[a,b]上单调递减,在区间[b,c]上单调递增则函数y=f(x)在x=b处有最小值f(b).利用函数单调性判断函数的最大(小)值的方法1.求函数的单调区间;2.判断函数的单调性(证明);5.求函数的最值或值域3.比较函数的大小函数单调性的应用4.求参数的取值范围 【例1】函数 y=x2 -2|x|-3 的单调递增区间是____________;[-1,0],[1,+?)-21-1一、求函数的单调区间【1】 求函数 y=|x+1|-|1-x| 的单调区间.解:由 y = | x + 1 |-|1-x |,知故函数的增区间为[-1, 1].练一练【2】画出函数y = |x2-2x-3|的图象.解:当 x2-2x-3≥0 ,即 x ≤-1 或 x≥3 时,y = x2-2x-3=( x-1)2-4. 当 x2-2x-3<0, 即 -1<x<3时,y =-(x2-2x-3) =-(x-1)2+4. 【3】求函数y=2|x-1|-3|x|的最大值.解:(1)当x<0时,y=-2(x-1)+3x=x+2;(2)当0≤x<1时,y=-2(x-1)-3x=-5x+2;(3)当x≥1时,y=2(x-1)+3x=-x-2.备课资料1.函数 的单调减区间为______.2.函数y=|2x-1|的单调增区间是______.巩固练习【例2】证明函数 在 上是减函数.二、判断(证明)函数的单调性证明:任取因此 在 上是减函数.【例2】证明函数 在二、判断(证明)函数的单调性上是减函数.另解:向上平移向左平移2 个单位3个单位所以函数f(x)的递减区间是 练一练【1】写出函数 的单调区间. 例3.已知函数 对任意实数t都有 比较f(1), f(2), f(3)的大小.三、利用单调性比较函数值的大小 【1】已知函数f(x)在(0,+∞)上是减函数,则
的大小关系为___________. 练一练1.设函数y=x2+2(a-1)x+2在区间[2,+?)上是增函数,求实数a的取值范围.解:函数y=x2+2(a-1)x+2的对称轴方程为x=1-a,函数的单调增区间是[1-a,+?),∴ [2,+?)是[1-a,+?)的一个子集,∴ 1-a≤2即a≥-1.即所求的实数取值范围是a≥-1.图象演示由二次函数性质知,四、利用函数单调性求参数的取值范围 【1】函数f(x)=x2+4ax+2在区间(-∞,6]内递减,则a的取值范围是………………( )
A.a≥3 B.a≤3
C.a≥-3 D.a≤-3D 【2】在已知函数f(x)=4x2-mx+1,在(-∞,-2]上递减,在[-2,+∞)上递增,则f(x)在[1,2]上的值域________.[21,39]练一练 【3】已知f(x)是R上的增函数, 若a+b>0,则有f(a)+f(b)>f(-a)+f(-b).证明:由a+b>0,得a>-b,b>-a.又因为f(x)是R上的增函数,∴ f(a) > f(-b), ① f(b)>f(-a), ②①+②得f(a)+f(b) >f(-a)+f(-b).练一练分析:设则确定 正负号的关键,是确定的正负号.由于x1, x2在同一区间内,要使 则需要使 则需例5.求函数 的最大值.五、求函数的最大(小)值或值域例5.求函数 的最大值.解:任取x1, x2 , x1, x2∈[2,4],且x1< x2,当 时,所以函数f(x)在[2,4]上是减函数.同理函数f(x)在[4,10]上是增函数.五、求函数的最大(小)值或值域解:∵函数在[2,4]上是减函数.所以f(x)在[2,4]上有最大值,∵函数在[4,10]上是增函数.所以f(x)在[4,10]上有最大值,所以函数f(x)在[2,10]上的最大值是几何画板 例6.函数f(x)是定义在(0,+?)上的递减函数,且f(x)< f(2x-3),求x的取值范围.解: ∵函数f(x) 在(0,+?)上为减函数,∴x的取值范围是.解之, 得模拟试验六、利用函数单调性解不等式 【1】已知函数y=f(x)在定义域R上是单调减函数,且f(a+1) > f(3-a),求实数a 的取值范围 【2】函数y=f(x)是定义在(-1,1)上的减函数,若f(2-a) > f(3-a),求实数a 的取值范围练一练【例3】求f(x)=x2-2ax+2在 [ 2,4 ]上的最小值.解:f (x) = (x-a) 2+2-a 2,① 当a<2时,②当2≤a<4 时, ③当a≥4时, ∴ f(x)min=f(2)=6-4a;f(x)在[ 2,4 ]上是增函数,∴ f(x)min=f(a)=2-a2.f(x)在[2,4]上是减函数.∴ f(x)min=f(4) = 18-8a.几何画板七、有关最值讨论题求最大值:① 当 a < 3 时, ② 当 a ≥ 3 时, f ( x ) max = f ( x ) max = f ( 4 ) = 18 -8af ( x ) max = f ( 2 ) = 6 -4a例6.已知f(x)=x2-4x-4,x∈[t,t+1](t∈R ),
求 f(x)的最小值g(t)的解析式.解:f(x)=(x-2)2-8(1)当2∈[t,t+2],即1≤t≤2时, g(t)=f(2)=-8;(2) 当 t > 2 时,∴g(t) = f(t)=t2-4t-4;(3)当t+1<2,即t<1时,f(x)在[t,t+1]上是减函数,∴g(t)=f(t+1)=t2-2t -7.综上所述:g ( t ) = f(x)在[t,t+1]上是增函数,教材P11 练习T4.教材P12 A组T7,9,10.作业布置再见2007年9月13日山东省临沂一中 李福国课堂小结1.函数单调性的定义:图象法定义法2.函数单调性的判定:3.函数单调性的应用:(1)设元:对任意x1,x2∈D,且x1<x2
(2)作差:f(x1)-f(x2)
(3)变形
(4)判号
(5)定论
*求函数 的单调区间. 若函数f(x),g(x)在给定的区间I上具有单调性,
(1)k>0时,函数y=f(x)与y=kf(x)+b具有相同的单调性;
(2)若f(x)恒为正或恒为负时,函数f(x)与1/f(x)具有相反的单调性.
(3)若函数f(x),g(x)都是增(减)函数,则f(x)+g(x)仍是增(减)函数.
(4)若f(x)>0,g(x)>0,且f(x)与g(x)都是增(减)函数,则f(x)·g(x)也是增(减)函数;若f(x)<0,g(x)<0,且f(x)与g(x)都是增(减)函数,则f(x)·g(x)是减(增)函数.单调性性质规律总结:(4)奇函数在对称的区间上有相同的单调性,偶函数在对称的区间上有相反的单调性.
(5)复合函数f[g(x)]的单调性由f(x)和g(x)的单调性共同决定(同则增异则减) .单调性性质规律总结:复合函数:y=f[g(x)]令 u=g(x)则 y=f(u)内函数外函数y=f[g(x)]原函数以x为自变量以u为自变量以x为自变量(5)复合函数的单调性复合函数单调性结论: ①当内外函数在各自定义域内同增同减时,原函数增; ②当内外函数在各自定义域内一增一减时,原函数减. (1)f(x)是[a,b]上增函数,若存在x1, x2∈[a,b]且x1
(4)若存在x1, x2∈[a,b]且x1
(4)若存在x1, x2∈[a,b]且x1
