第三章 勾股定理 单元测试（含答案）

中小学教育资源及组卷应用平台
《勾股定理》单元测试
一、选择题（每题3分，共30分）
1．一个直角三角形，两直角边长分别为3和4，下列说法正确的是（　　）
A．斜边长为5 B．三角形的周长为25 C．斜边长为25 D．三角形的面积为20
2．下列各组数中不能作为直角三角形的三边长的是（　　）
A．1.5，2，3 B．7，24，25 C．6，8，10 D．9，12，15
3．直角三角形两直角边长度为5，12，则斜边上的高（　　）
A．6 B.8 C. D.
4．小明想知道学校旗杆的高度，他发现旗杆上的绳子垂到地面还多1米，当他把绳子的下端拉开5米后，发现下端刚好接触地面，则旗杆的高是（　　）
A．8米 B．10米 C．12米 D．14米
5．在△ABC中，∠C=90°，周长为60，斜边与一直角边比是13：5，则这个三角形三边长分别是（　　）
A．5，4，3 B．13，12，5 C．10，8，6 D．26，24，10
6．下列各组线段中的三个长度：①9，12，15；②7，24，25；③32，42，52；④3a，4a，5a（a＞0）；
⑤m2﹣n2，2mn，m2+n2（m，n为正整数，且m＞n）其中可以构成直角三角形的有（　　）
A．5组 B．4组 C．3组 D．2组
7．下列结论错误的是（　　）
A．三个角度之比为1：2：3的三角形是直角三角形
B．三个边长之比为3：4：5的三角形是直角三角形
C．三个边长之比为8：16：17的三角形是直角三角形
D．三个角度之比为1：1：2的三角形是直角三角形
8．小明准备测量一段河水的深度，他把一根竹竿竖直插到离岸边1.5m远的水底，竹竿高出水面0.5m，把竹竿的顶端拉向岸边，竿顶和岸边的水面刚好相齐，则河水的深度为（　　）
A． 2m B．2.5m C．2.25m D．3m
9．小军量得家里新购置的彩电荧光屏的长为58厘米，宽为46厘米，则这台电视机的尺寸是（实际测量的误差可不计）（　　）
A．9英寸（23厘米） B．21英寸（54厘米）
C．29英寸（74厘米） D．34英寸（87厘米）
10．观察下列几组数据：（1）8，15，17；（2）7，12，15；（3）12，15，20；（4）7，24，25．其中能作为直角三角形三边长的有（　　）组．
A． 1 B．2 C．3 D．4
二、填空题（每题3分，共30分）
11．在Rt△ABC中，∠C=90°，（1）若a=5，b=12，则c=　_________　；（2）b=8，c=17，则
S△ABC=　_________　．
12．如果梯子的底端离建筑物9米，那么15米长的梯子可以到达建筑物的高度是　_________　米．
13．已知|x﹣6|+|y﹣8|+（z﹣10）2=0，则由此x，y，z为三边的三角形面积为　_________　．
14．在△ABC中，若三边长分别为9，12，15，则以这样的三角形拼成的矩形面积为　_________　．
15．△ABC中，AB=AC=17cm，BC=16cm，则高AD=　_________　cm．[]
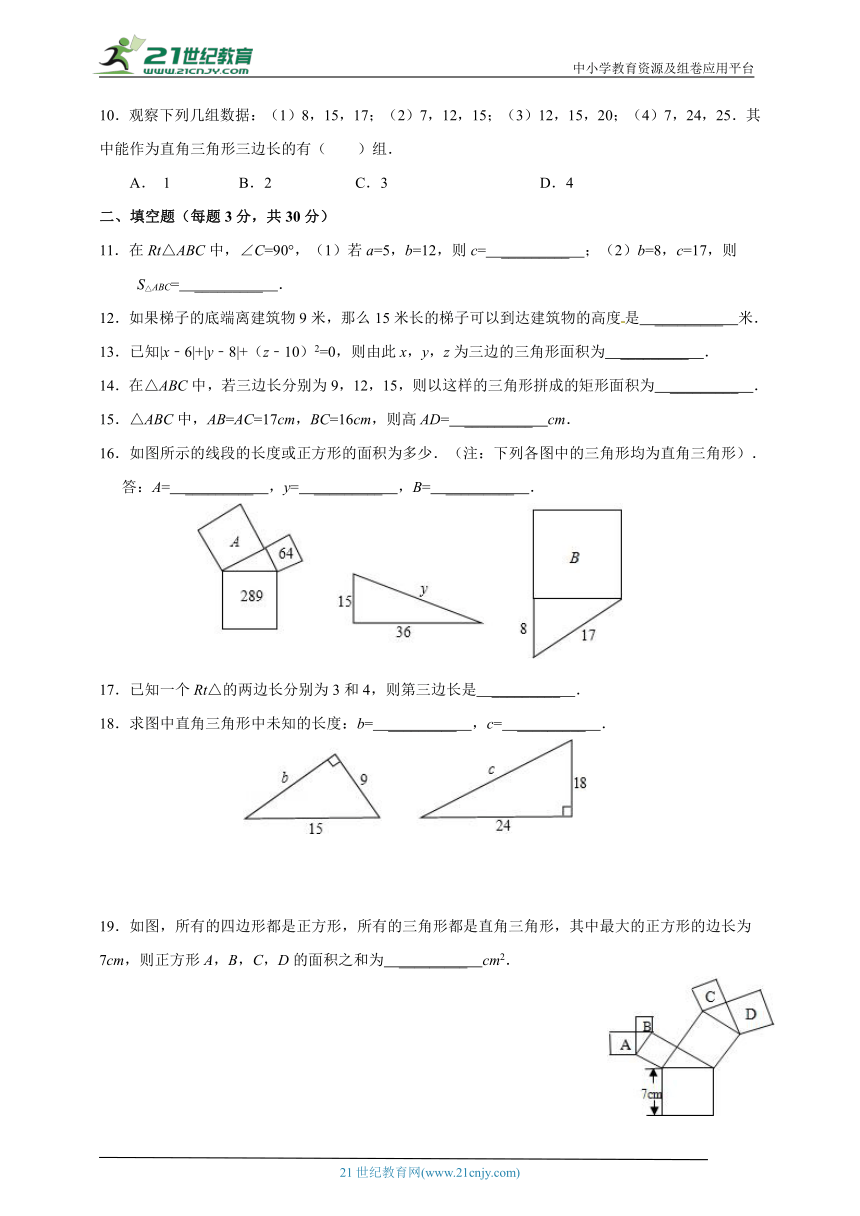
16．如图所示的线段的长度或正方形的面积为多少．（注：下列各图中的三角形均为直角三角形）．
答：A=　_________　，y=　_________　，B=　_________　．
17．已知一个Rt△的两边长分别为3和4，则第三边长是　_________　．
18．求图中直角三角形中未知的长度：b=　_________　，c=　_________　．
19．如图，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形的边长为7cm，则正方形A，B，C，D的面积之和为　_________　cm2．
20．已知三角形的三边长分别是2n+1，2n2+2n，2n2+2n+1，则最大角是　_________　度．
三、解答题（共60分）
21．（6分）做一做，如图每个小方格都是边长为1的正方形，求图中格点四边形ABCD的面积．
22．（6分）如图，一直角三角形三边长分别为6，8，10，且是三个圆的直径，求阴影部分面积（π取3.14）
23．（8分）一个三角形的三边长的比为3：4：5，那么这个三角形是直角三角形吗，为什么？
24．（8分）如图所示，为修铁路需凿通隧道AC，测得∠A=53°，∠B=37°．AB=5km，BC=4km，若每天凿0.3km，试计算需要几天才能把隧道AC凿通？
25．（8分）观察下列表格：请你结合该表格及相关知识，求出b，c的值．
列举 猜想
3、4、5 32=4+5
5、12、13 52=12+13
7、24、25 72=24+25
… …
35、b、c 352=b+c
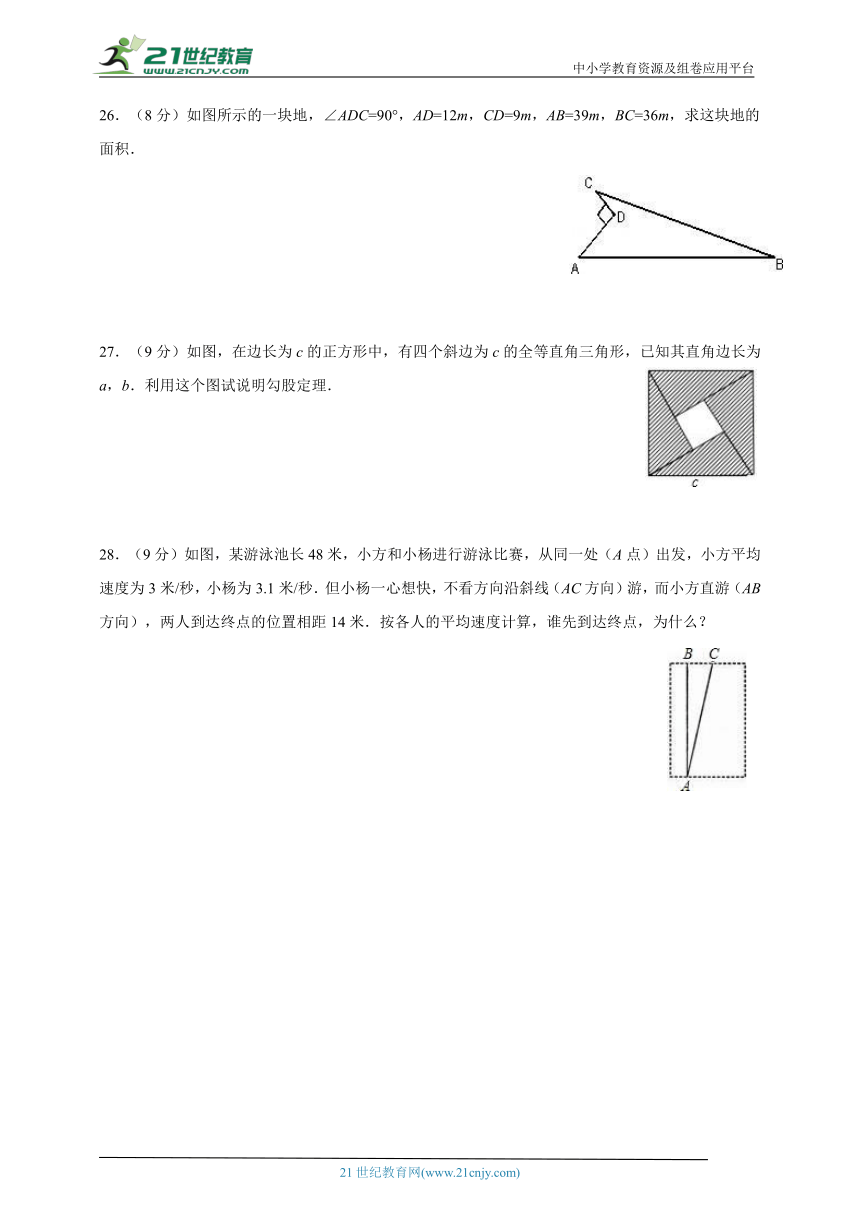
26．（8分）如图所示的一块地，∠ADC=90°，AD=12m，CD=9m，AB=39m，BC=36m，求这块地的面积．
27．（9分）如图，在边长为c的正方形中，有四个斜边为c的全等直角三角形，已知其直角边长为a，b．利用这个图试说明勾股定理．
28．（9分）如图，某游泳池长48米，小方和小杨进行游泳比赛，从同一处（A点）出发，小方平均速度为3米/秒，小杨为3.1米/秒．但小杨一心想快，不看方向沿斜线（AC方向）游，而小方直游（AB方向），两人到达终点的位置相距14米．按各人的平均速度计算，谁先到达终点，为什么？
参考答案
1，解：两直角边长分别为3和4，
∴斜边==5；
故选A．
2，解：A、1.52+22≠32，不符合勾股定理的逆定理，故正确；
B、72+242=252，符合勾股定理的逆定理，故错误；
C、62+82=102，符合勾股定理的逆定理，故错误；
D、92+122=152，符合勾股定理的逆定理，故错误．
故选A．
3，解：由题意得，斜边为=13．所以斜边上的高=12×5÷13=．
故选D．
4，解：画出示意图如下所示：
设旗杆的高AB为xm，则绳子AC的长为（x+1）m，
在Rt△ABC中，AB2+BC2=AC2，
∴x2+52=（x+1）2，
解得：x=12，
∴AB=12m，
即旗杆的高是12m．
故选C．
5，解：设斜边是13k，直角边是5k，
根据勾股定理，得另一条直角边是12k．
根据题意，得：13k+5k+12k=60
解得：k=2．则三边分别是26，24，10．
故选D．
6，解：①中有92+122=152；
②中有72+242=252；
③（32）2+（42）2≠（52）2；
④中有（3a）2+（4a）2=（5a）2；
⑤中有（m2﹣n2）2+（2mn）2=（m2+n2）2，所以可以构成4组直角三角形．
故选B．
7，解：A、因为根据三角形内角和定理可求出三个角分别为30°，60°，90°，所以该结论正确；
B、因为其三边符合勾股定理的逆定理，所以该结论正确；
C、因为其三边不符合勾股定理的逆定理，所以该结论不正确；
D、因为根据三角形内角和定理可求出三个角分别为45°，45°，90°，所以该结论正确．
故选C．
8，解：若假设竹竿长x米，则水深（x﹣0.5）米，由题意得，
x2=1.52+（x﹣0.5）2解之得，x=2.5
所以水深2.5﹣0.5=2米．
故选A．
9，解：根据勾股定理≈74．
故选C．
10，解：①82+152=172，根据勾股定理的逆定理是直角三角形，故正确；
②72+122≠152，根据勾股定理的逆定理不是直角三角形，故错误；
③122+152≠202，根据勾股定理的逆定理不是直角三角形，故错误；
④72+242=252，根据勾股定理的逆定理是直角三角形，故正确．
故选B．
11，解：（1）如图：∵在Rt△ABC中，∠C=90°，a=5，b=12，
∴c2=a2+b2=52+122=132，
∴c=13．
故答案是：13；
（2）如图：∵在Rt△ABC中，∠C=90°，b=8，c=17，
∴a==15，
∴S△ABC=ab=×15×8=60．
故答案是：60．
12，解：∵直角三角形的斜边长为15m，一直角边长为9m，
∴另一直角边长==12m，
故梯子可到达建筑物的高度是12m．
13，解：∵|x﹣6|+|y﹣8|+（z﹣10）2=0，
∴x﹣6=0，y﹣8=0，z﹣10=0，
∴x=6，y=8，z=10，
∵62+82=102，
∴x，y，z为三边的三角形是直角三角形，
∴S=6×8÷2=24．
故答案为：24．
14，解：∵92+122=152，∴根据勾股定理的逆定理，三角形是直角三角形，且两短边的边长分别为9，12，
∴以这样的三角形拼成的矩形面积为9×12=108．故填108．
15，解：∵等腰三角形底边上的高线、中线以及顶角平分线三线合一
∴BD=BC，
∵BC=16cm，
∴BD=BC=×16=8cm，
∵AB=AC=17cm，
∴AD====15cm．
16，解：根据勾股定理，A=289﹣64=225；
y===39；
B=172﹣82=289﹣64=225．
故答案为：225；39；225．
17，解：当长是3和4的两边是两条直角边时，第三边是斜边==5；
当长是3和4的两边一条是直角边，一条是斜边时，则长是4的一定是斜边，第三边是直角边==．
故第三边长是：5或．
故答案是：5或．
18，解：根据勾股定理得：b===12；
c===30．
故答案为：12，30．
19，解：由图形可知四个小正方形的面积和等于最大正方形的面积，故正方形A，B，C，D的面积之和=49cm2．
20，解：∵（2n+1）2+（2n2+2n）2=4n4+8n3+8n2+4n+1=（2n2+2n+1）2．
∴根据勾股定理的逆定理，三角形是直角三角形，则最大角为90°，故填90．
21，解：∵S△ADC=5×2÷2=5，S△ABC=5×3÷2=7.5，
∴四边形ABCD的面积=S△ADC+S△ABC=5+7.5=12.5．
22，解：根据题意可知：从小到大半圆的直径分别为6，8，10，
所以半径分别为：3，4，5，
则阴影部分的面积S=π×32+π×42+π×52=25π≈78.5．
23，解：是直角三角形；
因为边长之比满足3：4：5，
设三边分别为3x、4x、5x，
∵（3x）2+（4x）2=（5x）2，
即满足两边的平方和等于第三边的平方，
所以它是直角三角形．
24，解：∵∠A=53°，∠B=37°∴∠ACB=90°，
又∵在Rt△ABC中，AC2=AB2﹣BC2=52﹣42=9，∴AC=3，
需要的时间t===10（天）．
故需要10天才能把隧道AC凿通．
解：根据题意可知当n=13时，
b=（352﹣1）=612，
c=（352+1）=613．
26，解：连接AC，
已知，在直角△ACD中，CD=9m，AD=12m，
根据AD2+CD2=AC2，可以求得AC=15m，
在△ABC中，AB=39m，BC=36m，AC=15m，
∴存在AC2+CB2=AB2，
∴△ABC为直角三角形，
要求这块地的面积，求△ABC和△ACD的面积之差即可，
S=S△ABC﹣S△ACD=AC BC﹣CD AD，
=×15×36﹣×9×12，
=270﹣54，
=216m2，
答：这块地的面积为216m2．
27，解：∵大正方形面积为：c2，直角三角形面积为ab，小正方形面积为：（a﹣b）2，
所以c2=4×ab+（a﹣b）2，
即c2=a2+b2，
在每个直角边为a、b而斜边为c的直角三角形中，这个式子就是勾股定理．
28，解：如图，AB表示小方的路线，AC表示小杨的路线，
由题意可知，AB=48，BC=14，
在直角三角形ABC中，AC==50，
小方用时：=16秒，小杨用时秒，
因为16，所以小方用时少，即小方先到达终点．
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)