1.3.2(1)函数的奇偶性
图片预览








文档简介
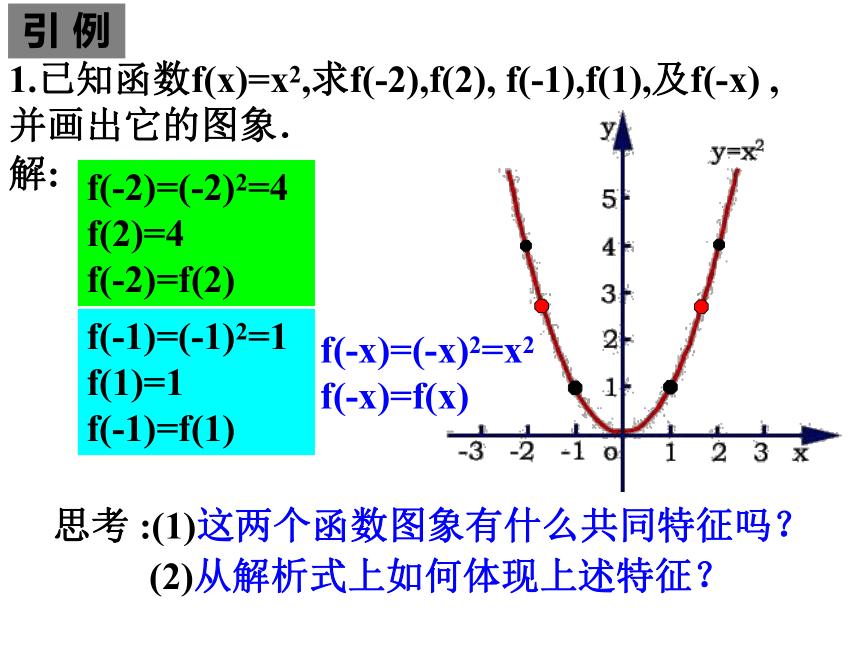
课件32张PPT。函数的奇偶性书 山 有 路 勤 为 径,学 海 无 崖 苦 作 舟少 壮 不 努 力 ,老 大 徒 伤 悲 成功=艰苦的劳动+正确的方法+少谈空话天才就是百分之一的灵感加上百分之九十九的汗水! 勤 奋、守 纪、团结、进取!教学目标奇函数的概念;偶函数的概念;函数奇偶性的判断;【重点】函数奇偶性的概念【难点】函数奇偶性的判断【教法】自学辅导法、讨论法、讲授法【学法】归纳——讨论——练习【教学手段】多媒体电脑与投影仪引 例1.已知函数f(x)=x2,求f(-2),f(2), f(-1),f(1),及f(-x) ,并画出它的图象.解:f(-2)=(-2)2=4 f(2)=4
f(-2)=f(2)f(-1)=(-1)2=1 f(1)=1
f(-1)=f(1)f(-x)=(-x)2=x2
f(-x)=f(x)思考 :(1)这两个函数图象有什么共同特征吗?
(2)从解析式上如何体现上述特征?
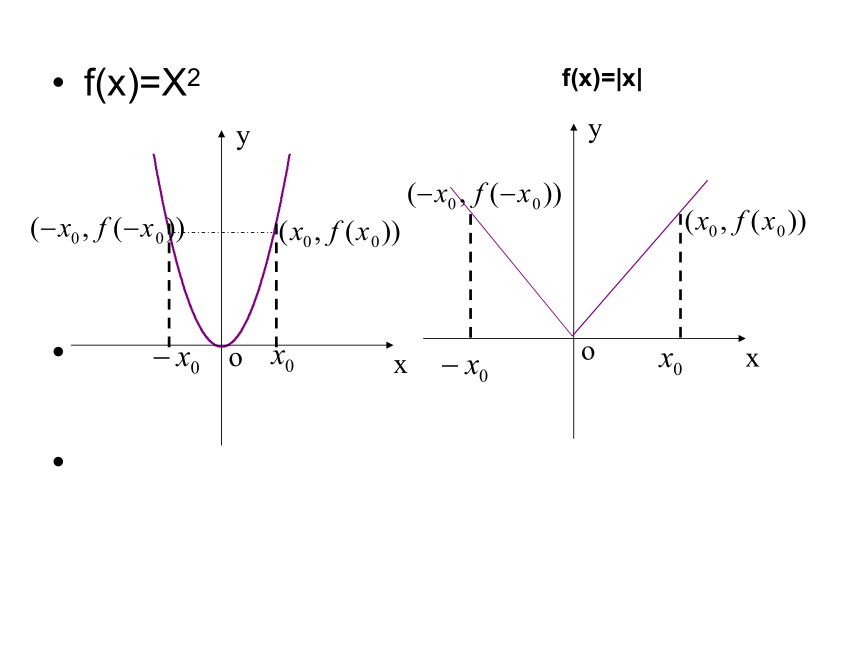
f(x)=X2 f(x)=|x|
根据图像发现了什么?
关于y轴对称
当自变量任取定义域中的两个相反数时,对应的函数值相等,即我们这节课所学的偶函数。
偶函数的定义:如果对于f(x)定义域内的任意一个x,都有f(-x)=f(x),
那么函数f(x)就叫偶函数.偶函数的特征:①解析式的基本特征:f (-x)=f (x)②图像特征:关于y轴对称. 如果对于函数f(x)的定义域内任意一个x,都有f(-x)=f(x),那么函数f(x)就叫做偶函数(even fun_ction).1. 偶函数的概念
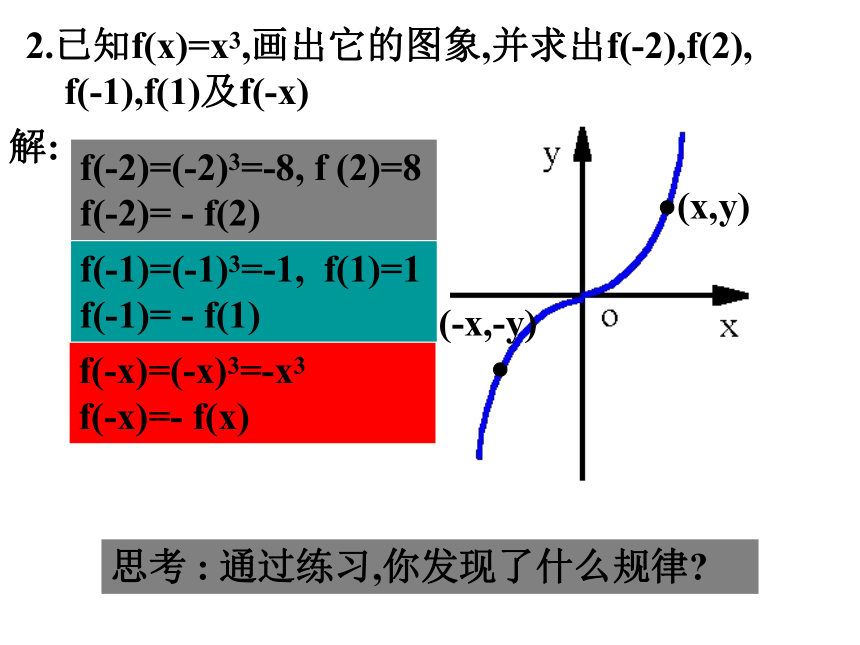
2.已知f(x)=x3,画出它的图象,并求出f(-2),f(2),
f(-1),f(1)及f(-x)解:f(-2)=(-2)3=-8, f (2)=8
f(-2)= - f(2)f(-1)=(-1)3=-1, f(1)=1 f(-1)= - f(1)f(-x)=(-x)3=-x3 f(-x)=- f(x)思考 : 通过练习,你发现了什么规律?(-x,-y)(x,y)接下来再看看我们常见的几个函数图像
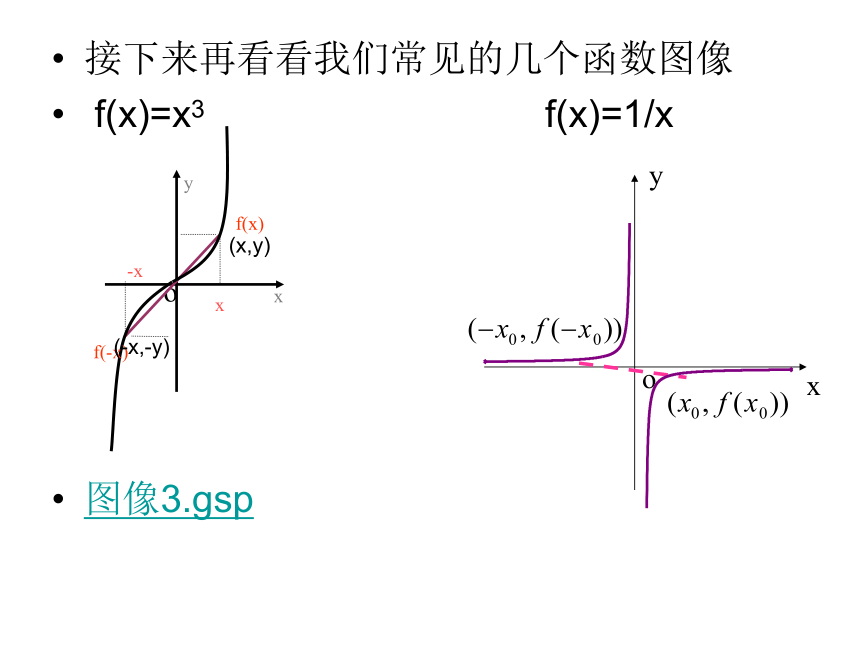
f(x)=x3 f(x)=1/x
图像3.gsp
xf(x)-xf(-x)(x,y)(-x,-y)根据图像发现了什么?
关于原点对称
当自变量任取定义域中的两个相反数时,对应的函数值相反,即我们这节课所学的奇函数。
奇函数的定义:如果对于f(x)定义域内的任意一个x,都有f(-x)=-f(x),
那么函数f(x)就叫奇函数.
为奇函数,定义域为R,0 判断函数奇偶性的前提条件是什么 定义域关于原点对称是函数具有奇偶性的前提条件。判断函数的奇偶性为什么要定义域关于原点对称判断函数的奇偶性的步骤:先看定义域是否关于原点对称
再看是否对于定义域内任意x都满足 奇函数的特征:①解析式的基本特征:f (-x)=-f (x)②图像特征:关于原点对称. 如果对于函数f(x)的定义域内任意一个x,都有f(-x)=-f(x),那么函数f(x)就叫做奇函数(odd fun_ction).2.奇函数的概念 如果一个函数f(x)是奇函数或偶函数,那么我们就说函数f(x)具有奇偶性.(1)奇、偶函数定义的逆命题也成立,即若f(x)为奇函数, 则f(-x)=-f(x)成立.若f(x)为偶函数, 则f(-x)= f(x) 成立.(2)判断函数是否具有奇偶性.首先要看函数的定义域是否关于原点对称,即函数定义域关于原点对称是函数具有奇偶性的前提.注意事项注意: (1)函数是奇函数或是偶函数称为函数的奇偶性,函数的奇偶性是函数的整体性质;而函数的单调性是函数的局部性质. (2)由函数的奇偶性定义可知,函数具有奇偶性的一个必要条件是,对于定义域内的任意一个x,则-x也一定是定义域内的一个自变量(即定义域关于原点对称). (3)奇、偶函数定义的逆命题也成立,即
若f(x)为奇函数,则f(-x)=-f(x)有成立.
若f(x)为偶函数,则f(-x)=f(x)有成立. (4)如果一个函数f(x)是奇函数或偶函数,那么我们就说函数f(x)具有奇偶性.(5)、若一个函数f(x)是奇函数,且当x=0时有定义, 则: f(0)=0注:1.奇、偶函数的定义域一定关于原点对称.例1.判断下列函数的奇偶性 定义域不对称的函数无奇偶性,既不是奇函数也不是偶函数。 例2. 函数 是定义在
上的偶函数,则该函数的值域是_____.例3.判断下列函数的奇偶性 定义域对称的非零常数函数仅是偶函数,而零函数既是奇函数又是偶函数.2.奇偶函数图象的性质:(2)偶函数的图象关于y轴对称.反过来,如果一个函数的图象关于y轴对称,那么这个函数为偶函数.奇偶函数图象的性质可用于:
① 判断函数的奇偶性.
②简化函数图象的画法,(1)奇函数的图象关于原点对称.反过来,如果一个函数的图象关于原点对称,那么这个函数为奇函数.例1. 判断下列函数的奇偶性(1) f(x)=x3+2x; (2) f(x)=2x4+3x2;解:∵f(-x)=(-x)3+2(-x)= -x3-2x= -(x3+2x)= - f(x),∴f(x)为奇函数. ∵f(-x)=2(-x)4+3(-x)2=2x4+3x2∴f(x)为偶函数.函数定义域为R.解:函数定义域为R.= f(x),巩固双基解:函数定义域为R.∴f(x)为奇函数.有既奇又偶的函数来吗?解:函数定义域为 [0 ,+∞).
∵ 定义域不关于原点对称,
∴f(x)为非奇非偶函数.(6) f(x)=x+1解:函数f(x)的定义域为R.
∵ f(-x)=f(x)=0,
又 f(-x)=-f(x)=0,
∴f(x)为既奇又偶函数.(5)f(x)=0 (x?R)根据奇偶性, 函数可划分为四类:奇函数;偶函数;
既奇又偶函数;
非奇非偶函数.
解:函数定义域为R.
∵ f(-x)= -x+1, - f(x)= -x-1,
∴f(-x)≠f(x),且f(-x)≠ –f(x).
∴f(x)为非奇非偶函数.判定函数的奇偶性的步骤:
(1)先求函数的定义域;
①若定义域不是关于原点对称的区间,则函数为非奇非偶函数.
②若定义域是关于原点对称的区间,进入第二步;
(2)计算f(-x)化向 f ( x ) 的解析式;
①若等于 f ( x ),则函数是偶函数,
②若等于-f ( x ),则函数是奇函数,
③若不等于 ,则函数是非奇非偶函数
(3)结论.有时判定f(-x)=±f(x)比较困难,可考虑判定f(-x)±f(x)=0或判定f(x)/f(-x)=±1. 练习2.判断下列函数的奇偶性∴f(x)为奇函数.解:定义域为{x|x≠0},即 f(-x)= - f(x),(3)f(x)=5解:f(x)的定义域为R.
∵ f(-x)=f(x)=5∴f(x)为偶函数.(4)f(x)=|x+1|-|x-1|∴f(x)既是偶函数, 又是奇函数. 解:函数的定义域为{-1,1},例4.若函数
是偶函数,求m的值.复习回顾1.两个定义: 对于f(x)定义域内的任意一个x ,
如果都有f(-x)=-f(x)?f(x)为奇函数.
如果都有f(-x)=f(x) ?f(x)为偶函数.一个函数为奇函数?它的图象关于原点对称.一个函数为偶函数?它的图象关于y 轴对称.2.两个性质:3.判断函数奇偶性的步骤
①考查函数定义域是否关于原点对称;
②判断f(-x)=±f(x)之一是否成立;
③作出结论.作业:课本P42 练习2, P46102.设y=f(x)为R上的任一函数,判断下列函数的奇偶性:
(1). F(x)=f(x)+f(- x) (2)F(x)=f(x)-f(-x)课堂作业课外作业学案P.22-23山东省临沂第一中学 李福国祝同学们学习进步!例3.已知f(x)是奇函数,当x≥0时,f(x)=x2-2x,求当 x<0时,f(x)的解析式,并画出此函数f(x)的图象.解:∵f(x)是奇函数,∴f(-x)=-f(x).∵当x≥0时,f(x)=x2-2x,∴当x<0时,-x>0,f(-x) = (-x)2-2(-x) = x2+2x,即 -f(x)= (x2+2x),∴ f(x)=-x2-2x.
f(-2)=f(2)f(-1)=(-1)2=1 f(1)=1
f(-1)=f(1)f(-x)=(-x)2=x2
f(-x)=f(x)思考 :(1)这两个函数图象有什么共同特征吗?
(2)从解析式上如何体现上述特征?
f(x)=X2 f(x)=|x|
根据图像发现了什么?
关于y轴对称
当自变量任取定义域中的两个相反数时,对应的函数值相等,即我们这节课所学的偶函数。
偶函数的定义:如果对于f(x)定义域内的任意一个x,都有f(-x)=f(x),
那么函数f(x)就叫偶函数.偶函数的特征:①解析式的基本特征:f (-x)=f (x)②图像特征:关于y轴对称. 如果对于函数f(x)的定义域内任意一个x,都有f(-x)=f(x),那么函数f(x)就叫做偶函数(even fun_ction).1. 偶函数的概念
2.已知f(x)=x3,画出它的图象,并求出f(-2),f(2),
f(-1),f(1)及f(-x)解:f(-2)=(-2)3=-8, f (2)=8
f(-2)= - f(2)f(-1)=(-1)3=-1, f(1)=1 f(-1)= - f(1)f(-x)=(-x)3=-x3 f(-x)=- f(x)思考 : 通过练习,你发现了什么规律?(-x,-y)(x,y)接下来再看看我们常见的几个函数图像
f(x)=x3 f(x)=1/x
图像3.gsp
xf(x)-xf(-x)(x,y)(-x,-y)根据图像发现了什么?
关于原点对称
当自变量任取定义域中的两个相反数时,对应的函数值相反,即我们这节课所学的奇函数。
奇函数的定义:如果对于f(x)定义域内的任意一个x,都有f(-x)=-f(x),
那么函数f(x)就叫奇函数.
为奇函数,定义域为R,0 判断函数奇偶性的前提条件是什么 定义域关于原点对称是函数具有奇偶性的前提条件。判断函数的奇偶性为什么要定义域关于原点对称判断函数的奇偶性的步骤:先看定义域是否关于原点对称
再看是否对于定义域内任意x都满足 奇函数的特征:①解析式的基本特征:f (-x)=-f (x)②图像特征:关于原点对称. 如果对于函数f(x)的定义域内任意一个x,都有f(-x)=-f(x),那么函数f(x)就叫做奇函数(odd fun_ction).2.奇函数的概念 如果一个函数f(x)是奇函数或偶函数,那么我们就说函数f(x)具有奇偶性.(1)奇、偶函数定义的逆命题也成立,即若f(x)为奇函数, 则f(-x)=-f(x)成立.若f(x)为偶函数, 则f(-x)= f(x) 成立.(2)判断函数是否具有奇偶性.首先要看函数的定义域是否关于原点对称,即函数定义域关于原点对称是函数具有奇偶性的前提.注意事项注意: (1)函数是奇函数或是偶函数称为函数的奇偶性,函数的奇偶性是函数的整体性质;而函数的单调性是函数的局部性质. (2)由函数的奇偶性定义可知,函数具有奇偶性的一个必要条件是,对于定义域内的任意一个x,则-x也一定是定义域内的一个自变量(即定义域关于原点对称). (3)奇、偶函数定义的逆命题也成立,即
若f(x)为奇函数,则f(-x)=-f(x)有成立.
若f(x)为偶函数,则f(-x)=f(x)有成立. (4)如果一个函数f(x)是奇函数或偶函数,那么我们就说函数f(x)具有奇偶性.(5)、若一个函数f(x)是奇函数,且当x=0时有定义, 则: f(0)=0注:1.奇、偶函数的定义域一定关于原点对称.例1.判断下列函数的奇偶性 定义域不对称的函数无奇偶性,既不是奇函数也不是偶函数。 例2. 函数 是定义在
上的偶函数,则该函数的值域是_____.例3.判断下列函数的奇偶性 定义域对称的非零常数函数仅是偶函数,而零函数既是奇函数又是偶函数.2.奇偶函数图象的性质:(2)偶函数的图象关于y轴对称.反过来,如果一个函数的图象关于y轴对称,那么这个函数为偶函数.奇偶函数图象的性质可用于:
① 判断函数的奇偶性.
②简化函数图象的画法,(1)奇函数的图象关于原点对称.反过来,如果一个函数的图象关于原点对称,那么这个函数为奇函数.例1. 判断下列函数的奇偶性(1) f(x)=x3+2x; (2) f(x)=2x4+3x2;解:∵f(-x)=(-x)3+2(-x)= -x3-2x= -(x3+2x)= - f(x),∴f(x)为奇函数. ∵f(-x)=2(-x)4+3(-x)2=2x4+3x2∴f(x)为偶函数.函数定义域为R.解:函数定义域为R.= f(x),巩固双基解:函数定义域为R.∴f(x)为奇函数.有既奇又偶的函数来吗?解:函数定义域为 [0 ,+∞).
∵ 定义域不关于原点对称,
∴f(x)为非奇非偶函数.(6) f(x)=x+1解:函数f(x)的定义域为R.
∵ f(-x)=f(x)=0,
又 f(-x)=-f(x)=0,
∴f(x)为既奇又偶函数.(5)f(x)=0 (x?R)根据奇偶性, 函数可划分为四类:奇函数;偶函数;
既奇又偶函数;
非奇非偶函数.
解:函数定义域为R.
∵ f(-x)= -x+1, - f(x)= -x-1,
∴f(-x)≠f(x),且f(-x)≠ –f(x).
∴f(x)为非奇非偶函数.判定函数的奇偶性的步骤:
(1)先求函数的定义域;
①若定义域不是关于原点对称的区间,则函数为非奇非偶函数.
②若定义域是关于原点对称的区间,进入第二步;
(2)计算f(-x)化向 f ( x ) 的解析式;
①若等于 f ( x ),则函数是偶函数,
②若等于-f ( x ),则函数是奇函数,
③若不等于 ,则函数是非奇非偶函数
(3)结论.有时判定f(-x)=±f(x)比较困难,可考虑判定f(-x)±f(x)=0或判定f(x)/f(-x)=±1. 练习2.判断下列函数的奇偶性∴f(x)为奇函数.解:定义域为{x|x≠0},即 f(-x)= - f(x),(3)f(x)=5解:f(x)的定义域为R.
∵ f(-x)=f(x)=5∴f(x)为偶函数.(4)f(x)=|x+1|-|x-1|∴f(x)既是偶函数, 又是奇函数. 解:函数的定义域为{-1,1},例4.若函数
是偶函数,求m的值.复习回顾1.两个定义: 对于f(x)定义域内的任意一个x ,
如果都有f(-x)=-f(x)?f(x)为奇函数.
如果都有f(-x)=f(x) ?f(x)为偶函数.一个函数为奇函数?它的图象关于原点对称.一个函数为偶函数?它的图象关于y 轴对称.2.两个性质:3.判断函数奇偶性的步骤
①考查函数定义域是否关于原点对称;
②判断f(-x)=±f(x)之一是否成立;
③作出结论.作业:课本P42 练习2, P46102.设y=f(x)为R上的任一函数,判断下列函数的奇偶性:
(1). F(x)=f(x)+f(- x) (2)F(x)=f(x)-f(-x)课堂作业课外作业学案P.22-23山东省临沂第一中学 李福国祝同学们学习进步!例3.已知f(x)是奇函数,当x≥0时,f(x)=x2-2x,求当 x<0时,f(x)的解析式,并画出此函数f(x)的图象.解:∵f(x)是奇函数,∴f(-x)=-f(x).∵当x≥0时,f(x)=x2-2x,∴当x<0时,-x>0,f(-x) = (-x)2-2(-x) = x2+2x,即 -f(x)= (x2+2x),∴ f(x)=-x2-2x.
