华师大版九年级上册 24.2.用计算器求锐角三角函数值 (第1课时) 课件(共16张PPT)
文档属性
| 名称 | 华师大版九年级上册 24.2.用计算器求锐角三角函数值 (第1课时) 课件(共16张PPT) |
|
|
| 格式 | ppt | ||
| 文件大小 | 654.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-08 20:07:03 | ||
图片预览




文档简介
(共16张PPT)
锐角三角函数
探 索
小明某天去爬山,(山高约600米).他沿着一条笔直的约有3千米的山道向上爬,当他前进到A处时(如图所示)发现有一石碑,石碑上的信息告诉他,此地海拔高为400米,请你帮小明计算一下从开始爬山到A处,他前进的路程有多远?
A
O
D
C
B
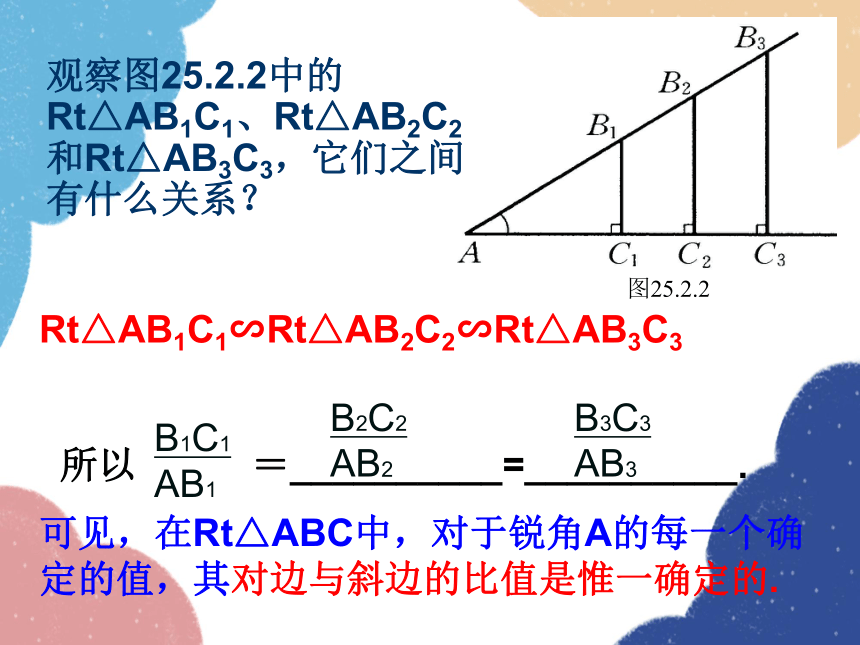
我们已经知道,直角三角形ABC可以简记为Rt△ABC,直角∠C所对的边AB称为斜边,用c表示,另两条直角边分别叫∠A的对边与邻边,用a、b表示.
温故知新
问题(1):画一个Rt△ABC,使∠C=90°,∠A=30°,并且算出∠A的对边与斜边的比值是多少?量一量,算一算。
问题(2):你画的三角形与你同伴化的三角形全等吗?算出的比值有什么关系?
问题(3):在问题(1)中当∠A=45°、60°时,∠A的对边与斜边的比值是多少?你和同伴的结果还相等吗?
做一做
一般情况下,在Rt△ABC中,当∠A取其他固定值时,∠A的对边与斜边的比值还会是一个固定值吗?
思考
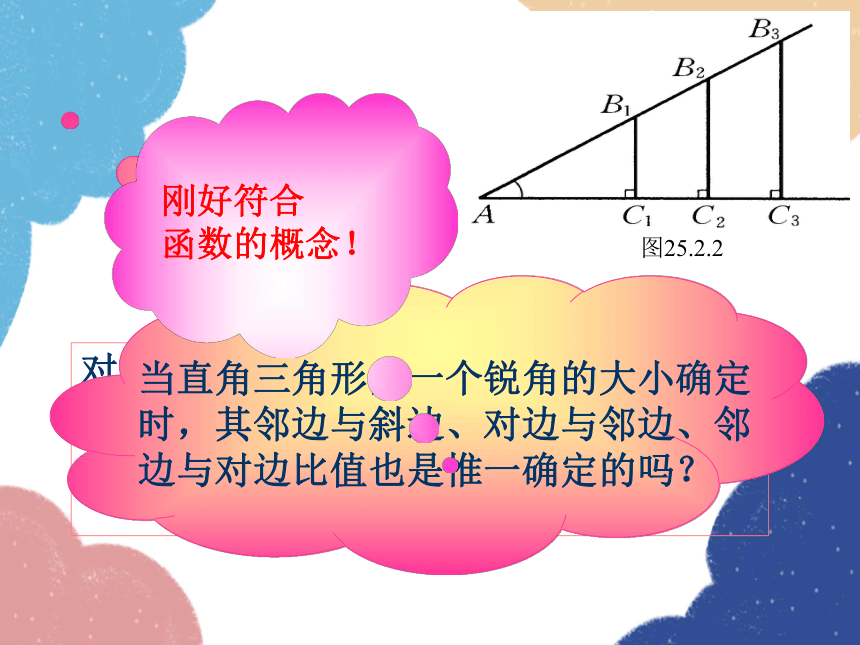
Rt△AB1C1∽Rt△AB2C2∽Rt△AB3C3
所以 =__________=__________.
可见,在Rt△ABC中,对于锐角A的每一个确定的值,其对边与斜边的比值是惟一确定的.
B2C2
AB2
B3C3
AB3
图25.2.2
B1C1
AB1
观察图25.2.2中的Rt△AB1C1、Rt△AB2C2和Rt△AB3C3,它们之间有什么关系?
对于锐角A的每一个确定的值,其对边与斜边、邻边与斜边、邻边与对边、对边与邻边的比值也都是惟一确定的。
想一想
当直角三角形的一个锐角的大小确定时,其邻边与斜边、对边与邻边、邻边与对边比值也是惟一确定的吗?
图25.2.2
刚好符合
函数的概念!
这几个比值都是锐角A的函数,记作
sin A、cos A、tan A、cot A,即
sin A=
cos A=
tan A=
cot A=
分别叫做锐角∠A的正弦、余弦、正切、余切,统称为锐角∠A的三角函数.
1、sinA 不是一个角 2、sinA不是 sin与A的乘积
3、 sinA 是一个比值 4、sinA 没有单位
=
=
=
=
1、你能利用直角三角形的三边关系得到sinA与 cosA的取值范围吗?
0<sin A<1,0<cos A<1
2、
tan A与cot A之间有什么关系?
tanA
=
cotA
=
sinA
=
cosA
=
tan A cot A=1
探 索
例1:求出图25.2.3所示的Rt△ABC中∠A的四个三角函数值.
8
15
图25.2.3
解:在Rt△ABC中:
AB= √BC2 +AC2
= √152+82 =17
sinA= ;cosA=
tanA= ;cotA=
变式1:如果将例(1)中条件“AC=15,BC=8”改为“AC:BC=1:2”,你能求出∠A的四个三角函数值吗?
变式训练
A
B
C
解:设AC=k (k>0),则由AC:BC=1:2得 ____ _
BC=2k,AB=√(2k)2+k2 =√5 k
sinA cosA
tanA cotA
变式2:如果将例(1)中条件“AC=15,BC=8”改为“cotA= ”,你能求出∠A的其他三个三角函数值吗?
变式训练
A
B
C
解:在Rt△ABC中,cotA= ,即
由AC:BC=1:2,则设AC=k (k>0),得 _ ___ _
BC=2k,AB=√(2k)2+k2 =√5 k
sinA cosA
tanA cotA
例题
例2:已知在△ABC中∠C=90°,sinA= BC=3,求AB,AC的长.
解:∵在Rt△ABC中,∠C=90°,sinA=
A
B
C
课 堂 小 结
☆一、基本概念
☆二、几个重要关系式
☆ 三、会利用三角函数所涉及的边角关系求解一些题目。
sinA
=
cosA
=
tanA
=
cotA
=
回味 无穷
通过本节课的学习你有什么收获和困惑?
1.课本习题25.2 的第一、二题。
课后作业
2.已知sinA= ,求∠A其余三角函数值。
3.等腰△ABC中,AB=AC=13,BC=10,求∠B的四种三角函数值。
谢谢各位指导!
锐角三角函数
探 索
小明某天去爬山,(山高约600米).他沿着一条笔直的约有3千米的山道向上爬,当他前进到A处时(如图所示)发现有一石碑,石碑上的信息告诉他,此地海拔高为400米,请你帮小明计算一下从开始爬山到A处,他前进的路程有多远?
A
O
D
C
B
我们已经知道,直角三角形ABC可以简记为Rt△ABC,直角∠C所对的边AB称为斜边,用c表示,另两条直角边分别叫∠A的对边与邻边,用a、b表示.
温故知新
问题(1):画一个Rt△ABC,使∠C=90°,∠A=30°,并且算出∠A的对边与斜边的比值是多少?量一量,算一算。
问题(2):你画的三角形与你同伴化的三角形全等吗?算出的比值有什么关系?
问题(3):在问题(1)中当∠A=45°、60°时,∠A的对边与斜边的比值是多少?你和同伴的结果还相等吗?
做一做
一般情况下,在Rt△ABC中,当∠A取其他固定值时,∠A的对边与斜边的比值还会是一个固定值吗?
思考
Rt△AB1C1∽Rt△AB2C2∽Rt△AB3C3
所以 =__________=__________.
可见,在Rt△ABC中,对于锐角A的每一个确定的值,其对边与斜边的比值是惟一确定的.
B2C2
AB2
B3C3
AB3
图25.2.2
B1C1
AB1
观察图25.2.2中的Rt△AB1C1、Rt△AB2C2和Rt△AB3C3,它们之间有什么关系?
对于锐角A的每一个确定的值,其对边与斜边、邻边与斜边、邻边与对边、对边与邻边的比值也都是惟一确定的。
想一想
当直角三角形的一个锐角的大小确定时,其邻边与斜边、对边与邻边、邻边与对边比值也是惟一确定的吗?
图25.2.2
刚好符合
函数的概念!
这几个比值都是锐角A的函数,记作
sin A、cos A、tan A、cot A,即
sin A=
cos A=
tan A=
cot A=
分别叫做锐角∠A的正弦、余弦、正切、余切,统称为锐角∠A的三角函数.
1、sinA 不是一个角 2、sinA不是 sin与A的乘积
3、 sinA 是一个比值 4、sinA 没有单位
=
=
=
=
1、你能利用直角三角形的三边关系得到sinA与 cosA的取值范围吗?
0<sin A<1,0<cos A<1
2、
tan A与cot A之间有什么关系?
tanA
=
cotA
=
sinA
=
cosA
=
tan A cot A=1
探 索
例1:求出图25.2.3所示的Rt△ABC中∠A的四个三角函数值.
8
15
图25.2.3
解:在Rt△ABC中:
AB= √BC2 +AC2
= √152+82 =17
sinA= ;cosA=
tanA= ;cotA=
变式1:如果将例(1)中条件“AC=15,BC=8”改为“AC:BC=1:2”,你能求出∠A的四个三角函数值吗?
变式训练
A
B
C
解:设AC=k (k>0),则由AC:BC=1:2得 ____ _
BC=2k,AB=√(2k)2+k2 =√5 k
sinA cosA
tanA cotA
变式2:如果将例(1)中条件“AC=15,BC=8”改为“cotA= ”,你能求出∠A的其他三个三角函数值吗?
变式训练
A
B
C
解:在Rt△ABC中,cotA= ,即
由AC:BC=1:2,则设AC=k (k>0),得 _ ___ _
BC=2k,AB=√(2k)2+k2 =√5 k
sinA cosA
tanA cotA
例题
例2:已知在△ABC中∠C=90°,sinA= BC=3,求AB,AC的长.
解:∵在Rt△ABC中,∠C=90°,sinA=
A
B
C
课 堂 小 结
☆一、基本概念
☆二、几个重要关系式
☆ 三、会利用三角函数所涉及的边角关系求解一些题目。
sinA
=
cosA
=
tanA
=
cotA
=
回味 无穷
通过本节课的学习你有什么收获和困惑?
1.课本习题25.2 的第一、二题。
课后作业
2.已知sinA= ,求∠A其余三角函数值。
3.等腰△ABC中,AB=AC=13,BC=10,求∠B的四种三角函数值。
谢谢各位指导!
