华师大版数学九年级上册 24.2 直角三角形的性质 课件(共14张PPT)
文档属性
| 名称 | 华师大版数学九年级上册 24.2 直角三角形的性质 课件(共14张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 515.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-08 20:09:32 | ||
图片预览



文档简介
(共14张PPT)
24.2 直角三角形的性质
导入新课
讲授新课
当堂练习
课堂小结
第24章 解直角三角形
1.理解直角三角形及在实际生活中的应用;(重点)
2.经历直角三角形的性质的猜想、演绎推理、证明过程,体会
探究过程中的乐趣.(难点)
学习目标
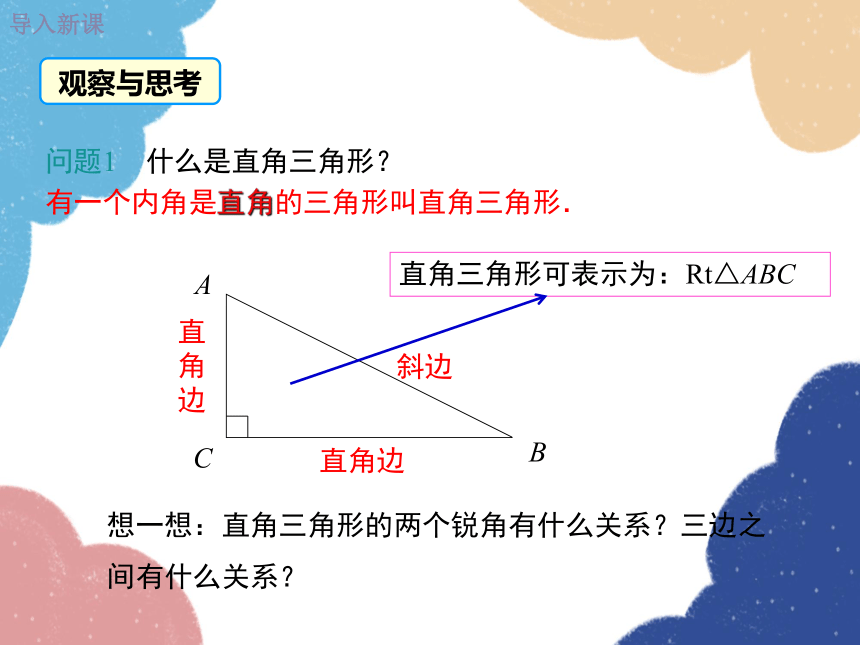
问题1 什么是直角三角形?
有一个内角是直角的三角形叫直角三角形.
直角三角形可表示为:Rt△ABC
A
C
B
斜边
直角边
直角边
想一想:直角三角形的两个锐角有什么关系?三边之间有什么关系?
导入新课
观察与思考
(1)直角三角形的两个锐角_________;
互余
(2)勾股定理:直角三角形两直角边的平方和______斜边的
平方.
等于
下面我们探索直角三角形的其他性质
问题2 你知道我们学过了直角三角形的哪些性质?
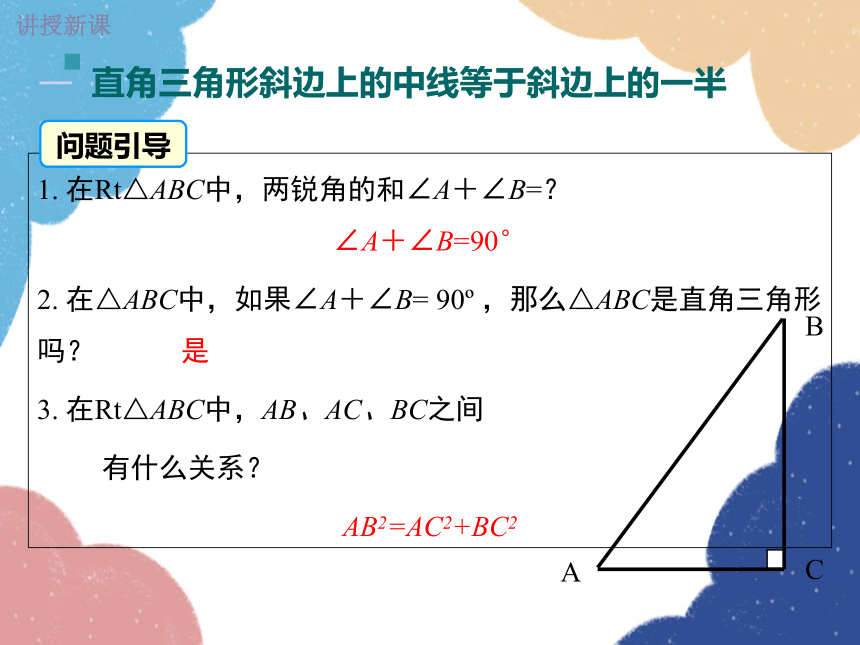
1. 在Rt△ABC中,两锐角的和∠A+∠B=?
∠A+∠B=90°
2. 在△ABC中,如果∠A+∠B= 90 ,那么△ABC是直角三角形吗? 是
3. 在Rt△ABC中,AB、AC、BC之间
有什么关系?
AB2=AC2+BC2
A
B
C
讲授新课
直角三角形斜边上的中线等于斜边上的一半
一
问题引导
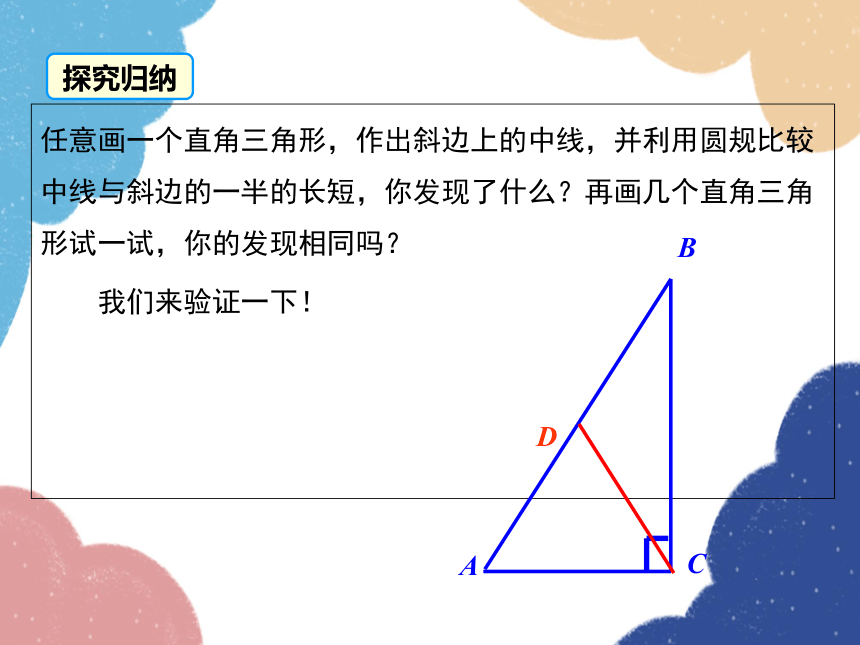
任意画一个直角三角形,作出斜边上的中线,并利用圆规比较中线与斜边的一半的长短,你发现了什么?再画几个直角三角形试一试,你的发现相同吗?
我们来验证一下!
A
B
C
D
探究归纳
直角三角形的性质之一
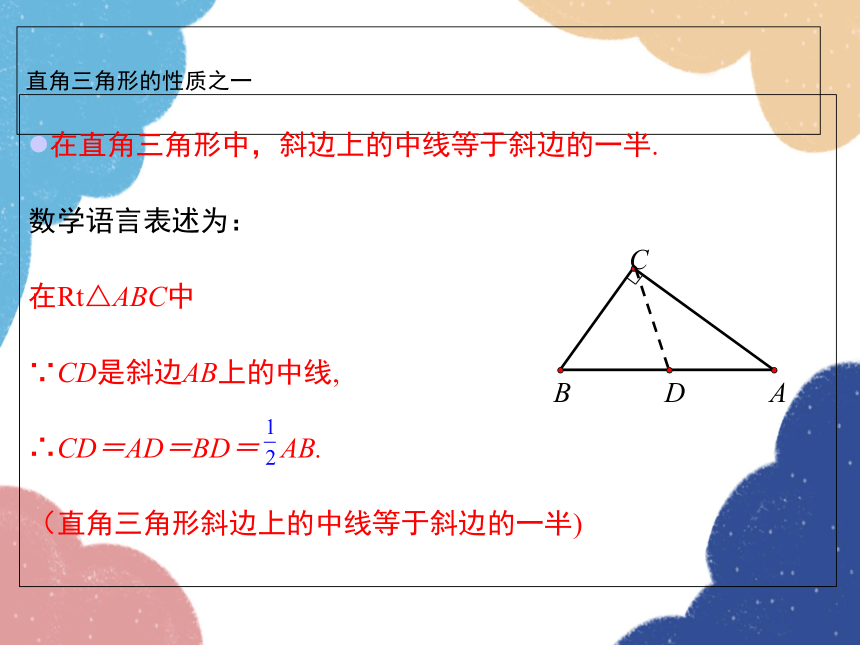
在直角三角形中,斜边上的中线等于斜边的一半.
数学语言表述为:
在Rt△ABC中
∵CD是斜边AB上的中线,
∴CD=AD=BD= AB.
(直角三角形斜边上的中线等于斜边的一半)
C
B
A
D
A
B
C
∟
D
【证明】
思路引导:
中线辅助线作法:将中线延长一倍.
延长CD到点E,使DE=CD,连结AE、BE.
E
∵ CD是斜边AB的中线,
∴ AD=BD.
又∵ DE=CD,
∴ 四边形ACBE是平行四边形.
又∵∠ACB=90 ,
∴ ACBE是矩形,
∴ CE=AB.
如图,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线.
求证:CD= AB.
1.已知Rt△ABC中,斜边AB=10cm,则斜边上的中线的长为______.
2.如图,在Rt△ABC中,CD是斜边AB上的中线∠CDA=80°,则∠A=_____ ,∠B=_____.
5cm
50°
40°
练一练
例 Rt△ABC中,∠ACB=90 ° ,∠A=30°,求证:BC= AB.
证明: 作斜边上的中线CD,
则CD=AD=BD= AB
(在直角三角形中,斜边上的中线等于斜边的一半)
∵ ∠A=30°
∴ ∠B=60°
∴ △CDB是等边三角形,
∴ BC=BD= AB
C
B
A
D
对此,你能得出什么结论?
直角三角形中,30°角所对的直角边等于斜边的一半
二
1.如图,在△ABC中,若∠BAC=120°,AB=AC, AD⊥AC于点A,BD=3,则BC=______.
9
当堂练习
2.如图, ∠C=90°,∠B=15°,DE垂直平分AB,垂足为点E,交BC边于点D,BD=16cm,则AC的长为______.
8cm
3.如图,在△ABC中,BD、CE是高,M、N分别是BC、ED的中点,试说明:MN⊥DE.
解:连结EM、DM.
∵BD、CE是高,M是BC中点,
∴在Rt△BCE和Rt△BCD中,
∴EM=DM.
又∵N是ED的中点,
∴MN⊥ED
N
M
D
E
B
C
A
,
,
BC
2
1
DM
BC
2
1
EM
=
=
我们学习了直角三角形哪些性质?
性质1
直角三角形两个锐角互余
性质2
直角三角形的勾股定理
性质3
直角三角形斜边上的中线等于斜边的一半
性质4
直角三角形30 角所对直角边等于斜边的一半
课堂小结
24.2 直角三角形的性质
导入新课
讲授新课
当堂练习
课堂小结
第24章 解直角三角形
1.理解直角三角形及在实际生活中的应用;(重点)
2.经历直角三角形的性质的猜想、演绎推理、证明过程,体会
探究过程中的乐趣.(难点)
学习目标
问题1 什么是直角三角形?
有一个内角是直角的三角形叫直角三角形.
直角三角形可表示为:Rt△ABC
A
C
B
斜边
直角边
直角边
想一想:直角三角形的两个锐角有什么关系?三边之间有什么关系?
导入新课
观察与思考
(1)直角三角形的两个锐角_________;
互余
(2)勾股定理:直角三角形两直角边的平方和______斜边的
平方.
等于
下面我们探索直角三角形的其他性质
问题2 你知道我们学过了直角三角形的哪些性质?
1. 在Rt△ABC中,两锐角的和∠A+∠B=?
∠A+∠B=90°
2. 在△ABC中,如果∠A+∠B= 90 ,那么△ABC是直角三角形吗? 是
3. 在Rt△ABC中,AB、AC、BC之间
有什么关系?
AB2=AC2+BC2
A
B
C
讲授新课
直角三角形斜边上的中线等于斜边上的一半
一
问题引导
任意画一个直角三角形,作出斜边上的中线,并利用圆规比较中线与斜边的一半的长短,你发现了什么?再画几个直角三角形试一试,你的发现相同吗?
我们来验证一下!
A
B
C
D
探究归纳
直角三角形的性质之一
在直角三角形中,斜边上的中线等于斜边的一半.
数学语言表述为:
在Rt△ABC中
∵CD是斜边AB上的中线,
∴CD=AD=BD= AB.
(直角三角形斜边上的中线等于斜边的一半)
C
B
A
D
A
B
C
∟
D
【证明】
思路引导:
中线辅助线作法:将中线延长一倍.
延长CD到点E,使DE=CD,连结AE、BE.
E
∵ CD是斜边AB的中线,
∴ AD=BD.
又∵ DE=CD,
∴ 四边形ACBE是平行四边形.
又∵∠ACB=90 ,
∴ ACBE是矩形,
∴ CE=AB.
如图,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线.
求证:CD= AB.
1.已知Rt△ABC中,斜边AB=10cm,则斜边上的中线的长为______.
2.如图,在Rt△ABC中,CD是斜边AB上的中线∠CDA=80°,则∠A=_____ ,∠B=_____.
5cm
50°
40°
练一练
例 Rt△ABC中,∠ACB=90 ° ,∠A=30°,求证:BC= AB.
证明: 作斜边上的中线CD,
则CD=AD=BD= AB
(在直角三角形中,斜边上的中线等于斜边的一半)
∵ ∠A=30°
∴ ∠B=60°
∴ △CDB是等边三角形,
∴ BC=BD= AB
C
B
A
D
对此,你能得出什么结论?
直角三角形中,30°角所对的直角边等于斜边的一半
二
1.如图,在△ABC中,若∠BAC=120°,AB=AC, AD⊥AC于点A,BD=3,则BC=______.
9
当堂练习
2.如图, ∠C=90°,∠B=15°,DE垂直平分AB,垂足为点E,交BC边于点D,BD=16cm,则AC的长为______.
8cm
3.如图,在△ABC中,BD、CE是高,M、N分别是BC、ED的中点,试说明:MN⊥DE.
解:连结EM、DM.
∵BD、CE是高,M是BC中点,
∴在Rt△BCE和Rt△BCD中,
∴EM=DM.
又∵N是ED的中点,
∴MN⊥ED
N
M
D
E
B
C
A
,
,
BC
2
1
DM
BC
2
1
EM
=
=
我们学习了直角三角形哪些性质?
性质1
直角三角形两个锐角互余
性质2
直角三角形的勾股定理
性质3
直角三角形斜边上的中线等于斜边的一半
性质4
直角三角形30 角所对直角边等于斜边的一半
课堂小结
