四川省2014届高三学业水平考试试卷 数学 高清图片版缺答案
文档属性
| 名称 | 四川省2014届高三学业水平考试试卷 数学 高清图片版缺答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 269.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-12-01 00:00:00 | ||
图片预览




文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
金华一中2013学年第一学期期中考试试题
高二 数学(文科)
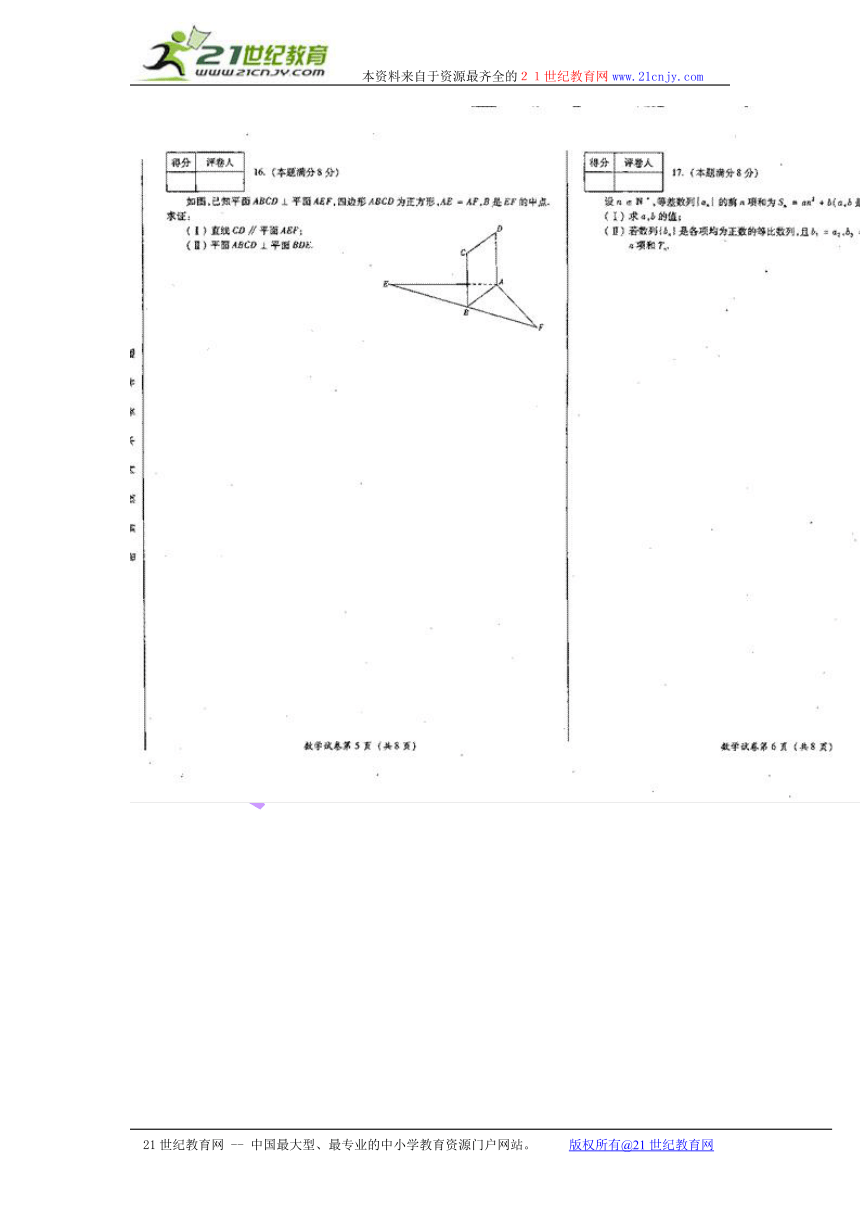
一、选择题(共10小题,每小题只有一个正确选项,每小题5分,共50分)
1,在直角坐标系中,直线的斜率是 ( )
A. B. C. D.
2,点在直线2x-y+5=0上,O为原点,则的最小值为 ( )
A. B. C. D.
3,点(1,2)关于直线 y = x1的对称点的坐标是 ( )
A.(3,2) B.(3,2) C.(3,2) D.(3,2)
4,已知平面α∥平面β,它们之间的距离为,直线,则在β内与直线相距为的直线有 ( )
A.1条 B.2条 C.无数条 D.不存在
5,下列说法中正确的是 ( )
A.“”是直线“与直线平行”的充要条件;
B.命题“”的否定是“”;
C.命题“若,则方程有实数根”的逆否命题为:“若方程无实数根,则”;
D.若为假命题,则p,q均为假命题。
6,一个几何体的三视图及部分数据如图所示,正视图、
侧视图和俯视图都是等腰直角三角形,则该几何体的
体积为 ( )
A. B.
C. D.1
7,已知是两条不同的直线,是三个不同的平面,则下列命题中正确的是( )
A.,则 B.,则
C.,则 D.,则
8,已知α,β表示两个不同的平面,,则“”是“”的 ( )
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
9,如图所示,点P在正方形ABCD所在平面外,PA⊥平面ABCD,
PA=AB,则PB与AC所成的角是 ( )
A.90° B.30°
C.45° D.60°
10,已知M为直线上任意一点,点,则过点M,N且与直线相切的圆的个数可能为 ( )
A .0或1 B.1或2 C.0,1或2 D.2
二、填空题(本大题共7小题,每小题4分,共28分。)
11,两条平行直线与间的距离是_________.
12,一球与棱长为2的正方体的各个面相切,则该球的表面积为 .
13,已知直线l1:ax+4y-2=0与直线l2:2x-5y+b=0互相垂直,垂足为(1,c),则c的值为_________.
14,已知p:|4-|≤6 , q: (m>0),若是的充分而不必要条件,则实数m的取值范围是________.
15,已知两圆和相交于A,B两点,则直线AB的方程为 .
16,已知菱形ABCD中,AB=2,∠A=120°,沿对角线BD将△ABD折起,使二面角A-BD-C为120°,则点A到△BCD所在平面的距离等于_ .
17,过直线:上一点作圆: 的切线,若关于直线对称,则点到圆心的距离为_ .
三、解答题(本大题共5小题,共72分,解答应写出文字说明,证明过程或演算步骤)
18,(本小题满分14分)
已知命题p:关于x的不等式对一切恒成立,q:函数是增函数,如果p∨q为真命题,p∧q为假命题,求实数的取值范围.
19,(本小题满分14分)
已知圆C:关于直线对称,圆心C在第四象限,半径为。
(Ⅰ)求圆C的方程;
(Ⅱ)是否存在直线与圆C相切,且在x轴上的截距是y轴上的截距的2倍?若存在,求直线的方程;若不存在,说明理由。
20,(本小题满分14分)
如图,在四棱锥中,底面为
正方形, 平面,已知.
(Ⅰ)求证:平面平面;
(Ⅱ)求直线与平面所成角的正弦值.
21,(本小题满分15分)
如图,平面PAC⊥平面ABC,AC⊥BC,△PAC为等边三角形,PE∥,M, N分别是线段,上的动点,且满足:
.
(Ⅰ) 求证:∥平面;
(Ⅱ) 当时,求平面ABC与平面MNC所成的锐二面角的大小.
22,(本小题满分15分)
如图,已知定圆,定直线,过的一条动直线与直线相交于,与圆相交于两点,是中点.
(Ⅰ)当与垂直时,求证:过圆心;
(Ⅱ)当时,求直线的方程;
(Ⅲ)设,试问是否为定值,
若为定值,请求出的值;若不为定值,
请说明理由.
金华一中2013学年第一学期期中考试答题卷
高二 数学(文科)
一、选择题:本大题共10小题,每小题5分,共50分。在每小题给出的四个选项
中,只有一项是符合题目要求的。
题目 1 2 3 4 5 6 7 8 9 10
答案
二、填空题:本大题共7小题,每小题4分,共28分。
11. 12 13.
14. 15. 16.
17.
三、解答题:本大题共5小题,共72分,解答应写出文字说明、证明过程或演算步骤.
18,(本小题满分14分)
已知命题p:关于x的不等式对一切恒成立,q:函数是增函数,如果p∨q为真命题,p∧q为假命题,求实数的取值范围.
19,(本小题满分14分)
已知圆C:关于直线对称,圆心C在第四象限,半径为。
(Ⅰ)求圆C的方程;
(Ⅱ)是否存在直线与圆C相切,且在x轴上的截距是y轴上的截距的2倍?若存在,求直线的方程;若不存在,说明理由。
20,(本小题满分14分)
如图,在四棱锥中,底面为
正方形, 平面,已知.
(Ⅰ)求证:平面平面;
(Ⅱ)求直线与平面所成角的正弦值.
21,(本小题满分15分)
如图,平面PAC⊥平面ABC,AC⊥BC,△PAC为等边三角形,PE∥,M, N分别是线段,上的动点,且满足:
.
(Ⅰ) 求证:∥平面;
(Ⅱ) 当时,求平面ABC与平面MNC所成的锐二面角的大小.
22,(本小题满分15分)
如图,已知定圆,定直线,过的一条动直线与直线相交于,与圆相交于两点,是中点.
(Ⅰ)当与垂直时,求证:过圆心;
(Ⅱ)当时,求直线的方程;
(Ⅲ)设,试问是否为定值,
若为定值,请求出的值;若不为定值,
请说明理由.
高二 数学(文科)参考答案
一,1—10 CADBC ABBDC
二,(11) (12) (13)-2 (14)[9,+∞ (15)
(16) (17)
18,解:由关于x的不等式对一切恒成立,得
∴ —————4分
函数是增函数,得
∴ —————8分
如果p真且q假,则,此不等式组无解;—————10分
如果p假且 q真,则,解得————————13分
所以实数a的取值范围为 ————————————14分
19,解:(Ⅰ)由得:
∴圆心C,半径,从而
解之得,
∴圆C的方程为 ……………7分
(Ⅱ)由(Ⅰ)知圆心C,设直线在x轴、y轴上的截距分别为
当时,设直线的方程为,则
解得,,此时直线的方程为 ……10分
当时,设直线的方程为即
则 ∴ 此时直线的方程为……13分
综上,存在四条直线满足题意,其方程为或
…………14分
20,(Ⅰ) 证明:由M、N分别是线段AE、AP上的中点,得MN∥PE,
又依题意PE∥BC,所以MN∥BC.
因为平面,平面,
所以//平面. …………7分
(Ⅱ)解:由(Ⅰ)知MN∥BC,故C、B、M、N共面,
平面ABC与平面MNC所成的锐二面角即N—CB—A.
因为平面PAC⊥平面ABC,平面PAC∩ 平面ABC = AC,且CB⊥AC,
所以CB⊥平面PAC.故CB⊥CN,
即知为二面角N—CB—A的平面角 ………12分
∵△PAC为等边三角形, N是线段的中点,
∴=30°
故平面ABC与平面MNC所成的锐二面角为30° ………15分
21.证明:(Ⅰ) 平面,平面, ,
, 平面,Ks*5u
平面,平面
∴平面平面 ………………7分
(Ⅱ)过作于,连结,由(Ⅰ) 平面平面
∴平面,为在平面内的射影,
为与平面的所成角的平面角, ………………10分
又平面,为直角三角形,
,且,. ……14分
22,解:(Ⅰ)由已知 ,故,所以直线的方程为.
将圆心代入方程易知过圆心 . ………………4分
(Ⅱ) 当直线与轴垂直时,易知符合题意;
当直线与轴不垂直时,设直线的方程为,由于,
所以由,解得.
故直线的方程为或. ………………9分
(Ⅲ)当与轴垂直时,易得,,又则
,
故. 即. ………………10分
当的斜率存在时,设直线的方程为,代入圆的方程得
,则
,即,
.又由得,
则.
故.
综上,的值为定值,且. …………15分
另解一:连结,延长交于点,由(Ⅰ)知.又于,
故△∽△.于是有.
由得
故 ………………………15分
另解二:连结并延长交直线于点,连结由(Ⅰ)知又,
所以四点都在以为直径的圆上,由相交弦定理得
. ……………15分
1
2
(第6题)
2
俯视图
正视图
侧视图
E
A
B
C
M
N
P
(第21题)
高( ) 班 姓名____________ 考号 试场座位号_________
E
A
B
C
M
N
P
(第21题)
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
金华一中2013学年第一学期期中考试试题
高二 数学(文科)
一、选择题(共10小题,每小题只有一个正确选项,每小题5分,共50分)
1,在直角坐标系中,直线的斜率是 ( )
A. B. C. D.
2,点在直线2x-y+5=0上,O为原点,则的最小值为 ( )
A. B. C. D.
3,点(1,2)关于直线 y = x1的对称点的坐标是 ( )
A.(3,2) B.(3,2) C.(3,2) D.(3,2)
4,已知平面α∥平面β,它们之间的距离为,直线,则在β内与直线相距为的直线有 ( )
A.1条 B.2条 C.无数条 D.不存在
5,下列说法中正确的是 ( )
A.“”是直线“与直线平行”的充要条件;
B.命题“”的否定是“”;
C.命题“若,则方程有实数根”的逆否命题为:“若方程无实数根,则”;
D.若为假命题,则p,q均为假命题。
6,一个几何体的三视图及部分数据如图所示,正视图、
侧视图和俯视图都是等腰直角三角形,则该几何体的
体积为 ( )
A. B.
C. D.1
7,已知是两条不同的直线,是三个不同的平面,则下列命题中正确的是( )
A.,则 B.,则
C.,则 D.,则
8,已知α,β表示两个不同的平面,,则“”是“”的 ( )
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
9,如图所示,点P在正方形ABCD所在平面外,PA⊥平面ABCD,
PA=AB,则PB与AC所成的角是 ( )
A.90° B.30°
C.45° D.60°
10,已知M为直线上任意一点,点,则过点M,N且与直线相切的圆的个数可能为 ( )
A .0或1 B.1或2 C.0,1或2 D.2
二、填空题(本大题共7小题,每小题4分,共28分。)
11,两条平行直线与间的距离是_________.
12,一球与棱长为2的正方体的各个面相切,则该球的表面积为 .
13,已知直线l1:ax+4y-2=0与直线l2:2x-5y+b=0互相垂直,垂足为(1,c),则c的值为_________.
14,已知p:|4-|≤6 , q: (m>0),若是的充分而不必要条件,则实数m的取值范围是________.
15,已知两圆和相交于A,B两点,则直线AB的方程为 .
16,已知菱形ABCD中,AB=2,∠A=120°,沿对角线BD将△ABD折起,使二面角A-BD-C为120°,则点A到△BCD所在平面的距离等于_ .
17,过直线:上一点作圆: 的切线,若关于直线对称,则点到圆心的距离为_ .
三、解答题(本大题共5小题,共72分,解答应写出文字说明,证明过程或演算步骤)
18,(本小题满分14分)
已知命题p:关于x的不等式对一切恒成立,q:函数是增函数,如果p∨q为真命题,p∧q为假命题,求实数的取值范围.
19,(本小题满分14分)
已知圆C:关于直线对称,圆心C在第四象限,半径为。
(Ⅰ)求圆C的方程;
(Ⅱ)是否存在直线与圆C相切,且在x轴上的截距是y轴上的截距的2倍?若存在,求直线的方程;若不存在,说明理由。
20,(本小题满分14分)
如图,在四棱锥中,底面为
正方形, 平面,已知.
(Ⅰ)求证:平面平面;
(Ⅱ)求直线与平面所成角的正弦值.
21,(本小题满分15分)
如图,平面PAC⊥平面ABC,AC⊥BC,△PAC为等边三角形,PE∥,M, N分别是线段,上的动点,且满足:
.
(Ⅰ) 求证:∥平面;
(Ⅱ) 当时,求平面ABC与平面MNC所成的锐二面角的大小.
22,(本小题满分15分)
如图,已知定圆,定直线,过的一条动直线与直线相交于,与圆相交于两点,是中点.
(Ⅰ)当与垂直时,求证:过圆心;
(Ⅱ)当时,求直线的方程;
(Ⅲ)设,试问是否为定值,
若为定值,请求出的值;若不为定值,
请说明理由.
金华一中2013学年第一学期期中考试答题卷
高二 数学(文科)
一、选择题:本大题共10小题,每小题5分,共50分。在每小题给出的四个选项
中,只有一项是符合题目要求的。
题目 1 2 3 4 5 6 7 8 9 10
答案
二、填空题:本大题共7小题,每小题4分,共28分。
11. 12 13.
14. 15. 16.
17.
三、解答题:本大题共5小题,共72分,解答应写出文字说明、证明过程或演算步骤.
18,(本小题满分14分)
已知命题p:关于x的不等式对一切恒成立,q:函数是增函数,如果p∨q为真命题,p∧q为假命题,求实数的取值范围.
19,(本小题满分14分)
已知圆C:关于直线对称,圆心C在第四象限,半径为。
(Ⅰ)求圆C的方程;
(Ⅱ)是否存在直线与圆C相切,且在x轴上的截距是y轴上的截距的2倍?若存在,求直线的方程;若不存在,说明理由。
20,(本小题满分14分)
如图,在四棱锥中,底面为
正方形, 平面,已知.
(Ⅰ)求证:平面平面;
(Ⅱ)求直线与平面所成角的正弦值.
21,(本小题满分15分)
如图,平面PAC⊥平面ABC,AC⊥BC,△PAC为等边三角形,PE∥,M, N分别是线段,上的动点,且满足:
.
(Ⅰ) 求证:∥平面;
(Ⅱ) 当时,求平面ABC与平面MNC所成的锐二面角的大小.
22,(本小题满分15分)
如图,已知定圆,定直线,过的一条动直线与直线相交于,与圆相交于两点,是中点.
(Ⅰ)当与垂直时,求证:过圆心;
(Ⅱ)当时,求直线的方程;
(Ⅲ)设,试问是否为定值,
若为定值,请求出的值;若不为定值,
请说明理由.
高二 数学(文科)参考答案
一,1—10 CADBC ABBDC
二,(11) (12) (13)-2 (14)[9,+∞ (15)
(16) (17)
18,解:由关于x的不等式对一切恒成立,得
∴ —————4分
函数是增函数,得
∴ —————8分
如果p真且q假,则,此不等式组无解;—————10分
如果p假且 q真,则,解得————————13分
所以实数a的取值范围为 ————————————14分
19,解:(Ⅰ)由得:
∴圆心C,半径,从而
解之得,
∴圆C的方程为 ……………7分
(Ⅱ)由(Ⅰ)知圆心C,设直线在x轴、y轴上的截距分别为
当时,设直线的方程为,则
解得,,此时直线的方程为 ……10分
当时,设直线的方程为即
则 ∴ 此时直线的方程为……13分
综上,存在四条直线满足题意,其方程为或
…………14分
20,(Ⅰ) 证明:由M、N分别是线段AE、AP上的中点,得MN∥PE,
又依题意PE∥BC,所以MN∥BC.
因为平面,平面,
所以//平面. …………7分
(Ⅱ)解:由(Ⅰ)知MN∥BC,故C、B、M、N共面,
平面ABC与平面MNC所成的锐二面角即N—CB—A.
因为平面PAC⊥平面ABC,平面PAC∩ 平面ABC = AC,且CB⊥AC,
所以CB⊥平面PAC.故CB⊥CN,
即知为二面角N—CB—A的平面角 ………12分
∵△PAC为等边三角形, N是线段的中点,
∴=30°
故平面ABC与平面MNC所成的锐二面角为30° ………15分
21.证明:(Ⅰ) 平面,平面, ,
, 平面,Ks*5u
平面,平面
∴平面平面 ………………7分
(Ⅱ)过作于,连结,由(Ⅰ) 平面平面
∴平面,为在平面内的射影,
为与平面的所成角的平面角, ………………10分
又平面,为直角三角形,
,且,. ……14分
22,解:(Ⅰ)由已知 ,故,所以直线的方程为.
将圆心代入方程易知过圆心 . ………………4分
(Ⅱ) 当直线与轴垂直时,易知符合题意;
当直线与轴不垂直时,设直线的方程为,由于,
所以由,解得.
故直线的方程为或. ………………9分
(Ⅲ)当与轴垂直时,易得,,又则
,
故. 即. ………………10分
当的斜率存在时,设直线的方程为,代入圆的方程得
,则
,即,
.又由得,
则.
故.
综上,的值为定值,且. …………15分
另解一:连结,延长交于点,由(Ⅰ)知.又于,
故△∽△.于是有.
由得
故 ………………………15分
另解二:连结并延长交直线于点,连结由(Ⅰ)知又,
所以四点都在以为直径的圆上,由相交弦定理得
. ……………15分
1
2
(第6题)
2
俯视图
正视图
侧视图
E
A
B
C
M
N
P
(第21题)
高( ) 班 姓名____________ 考号 试场座位号_________
E
A
B
C
M
N
P
(第21题)
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
同课章节目录
