直线与圆的位置关系[上学期]
文档属性
| 名称 | 直线与圆的位置关系[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 224.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-09-21 00:00:00 | ||
图片预览


文档简介
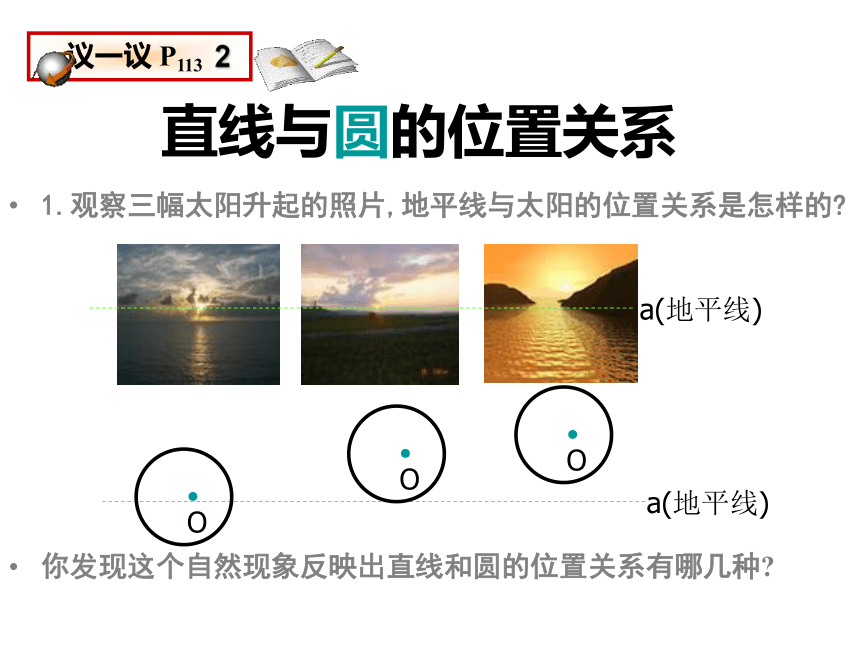
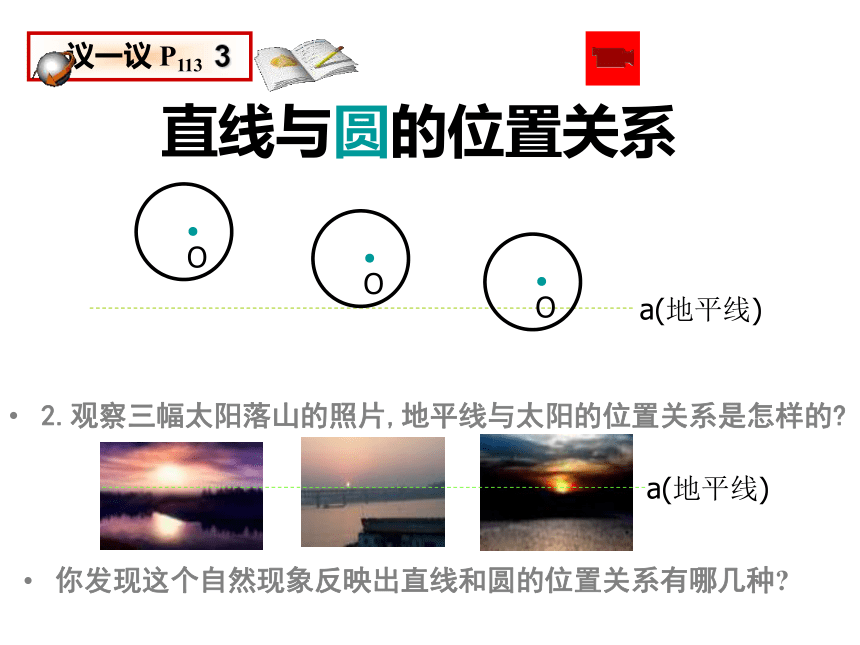
课件47张PPT。5.直线和圆的位置关系(1)直线与圆的位置关系1.观察三幅太阳升起的照片,地平线与太阳的位置关系是怎样的?你发现这个自然现象反映出直线和圆的位置关系有哪几种?a(地平线)a(地平线)直线与圆的位置关系2.观察三幅太阳落山的照片,地平线与太阳的位置关系是怎样的?你发现这个自然现象反映出直线和圆的位置关系有哪几种?a(地平线)a(地平线)直线与圆的位置关系
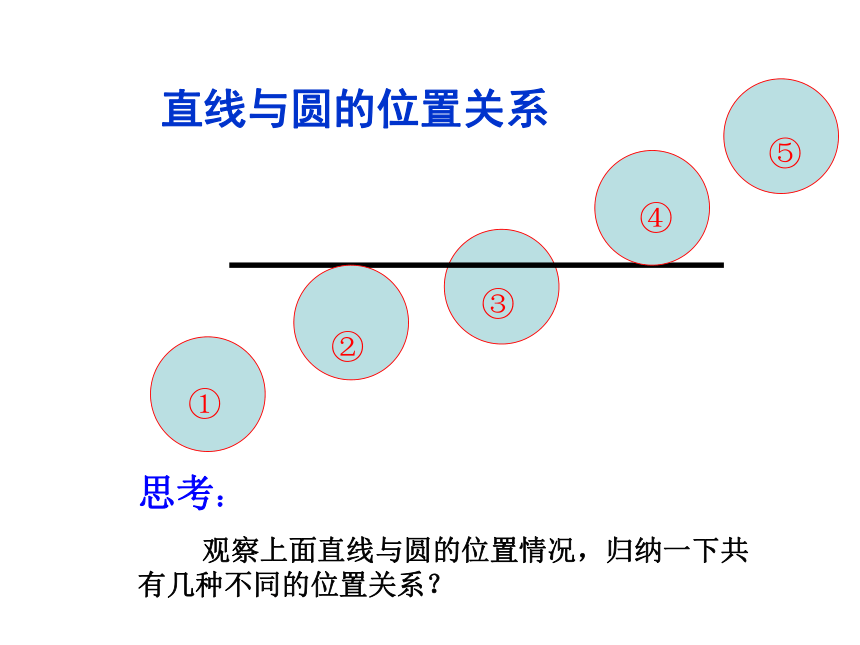
思考:
观察上面直线与圆的位置情况,归纳一下共有几种不同的位置关系?
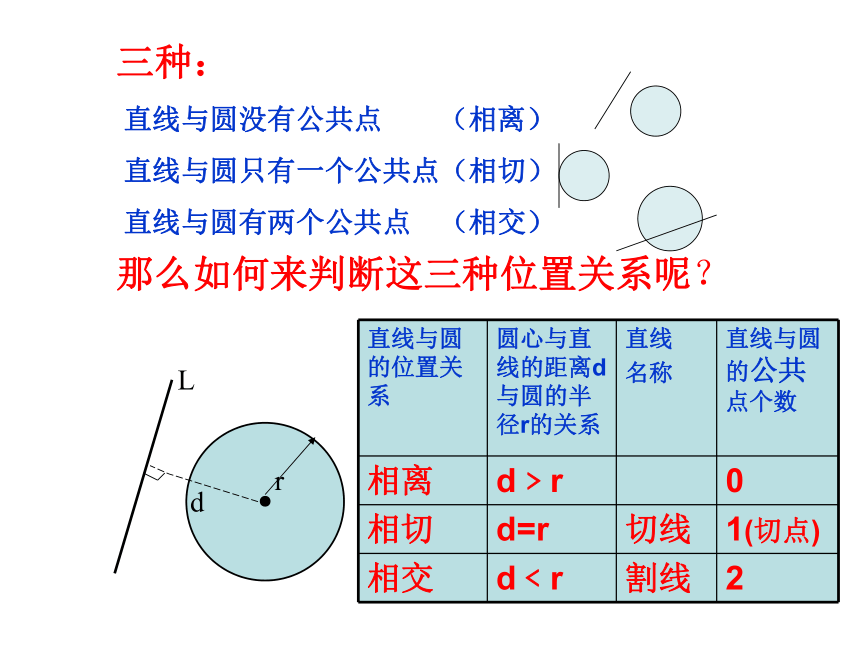
三种:
直线与圆没有公共点 (相离)
直线与圆只有一个公共点(相切)
直线与圆有两个公共点 (相交)那么如何来判断这三种位置关系呢?
1、已知的⊙O直径为5cm,直线L与圆心O之间的距离d。
(1)若d=2.5cm,则L与⊙O 有_______公共点,此时直线L与⊙O ___________.
(2)若d=3cm,则L与⊙O 有______公共点,此时直线L与⊙O __________.
(3)若d=1.5cm,则L与⊙O 有________公共点,此时直线L与⊙O __________.
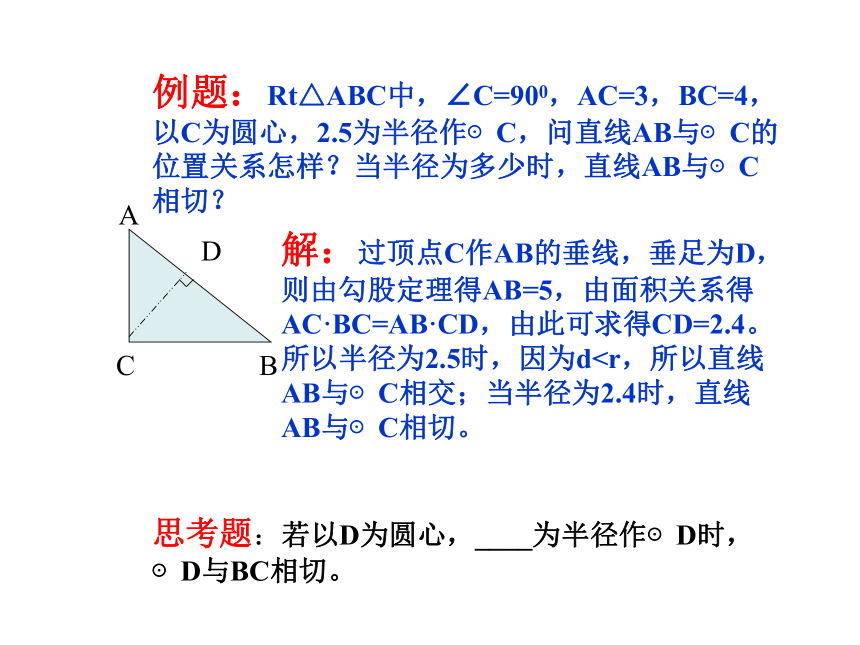
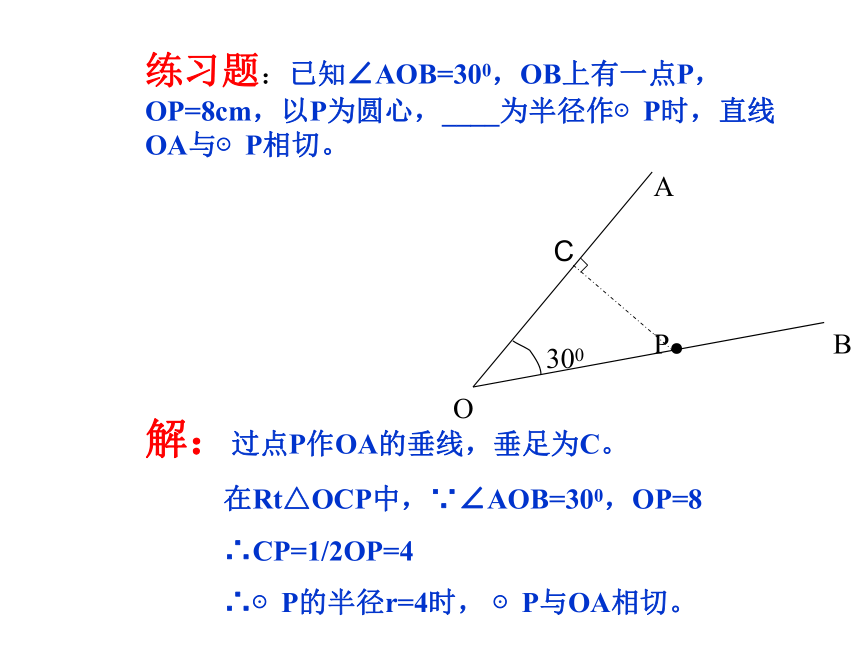
2、 ⊙O 的半径R=4cm,弦AB=4√3cm,以点O为圆心,2cm为半径的圆和AB的位置关系是___________练习题:例题:Rt△ABC中,∠C=900,AC=3,BC=4,以C为圆心,2.5为半径作⊙C,问直线AB与⊙C的位置关系怎样?当半径为多少时,直线AB与⊙C相切?解:过顶点C作AB的垂线,垂足为D,则由勾股定理得AB=5,由面积关系得AC·BC=AB·CD,由此可求得CD=2.4。所以半径为2.5时,因为d 在Rt△OCP中,∵∠AOB=300,OP=8
∴CP=1/2OP=4
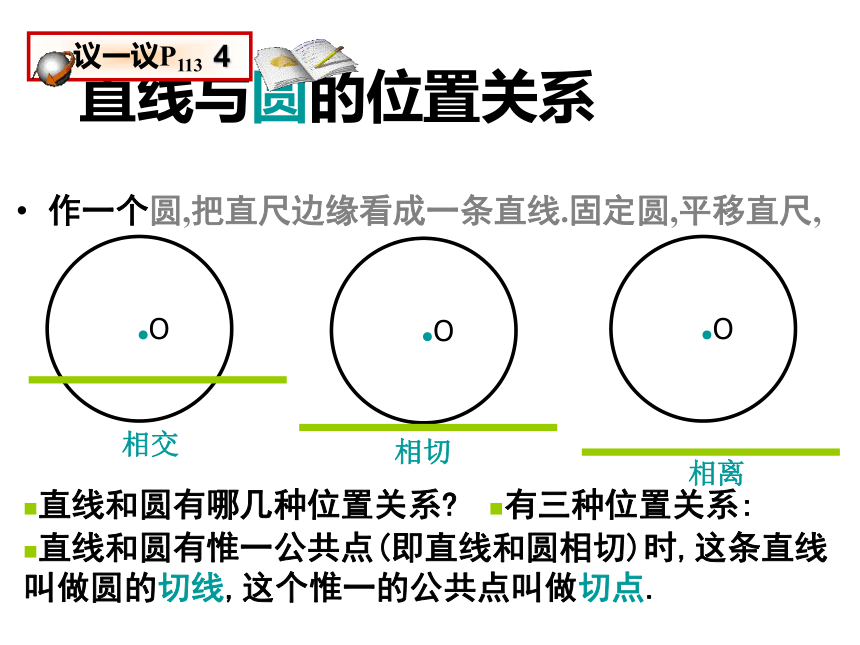
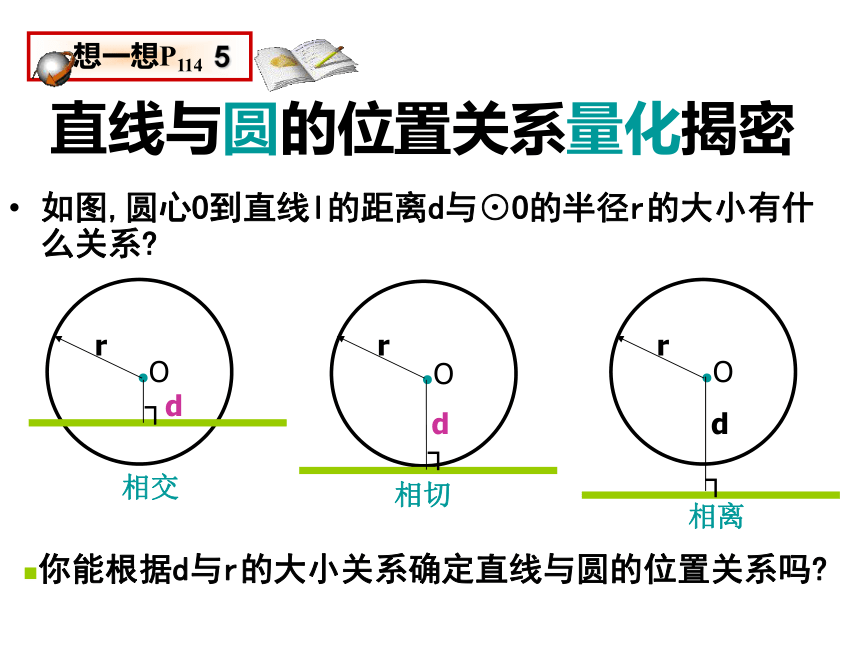
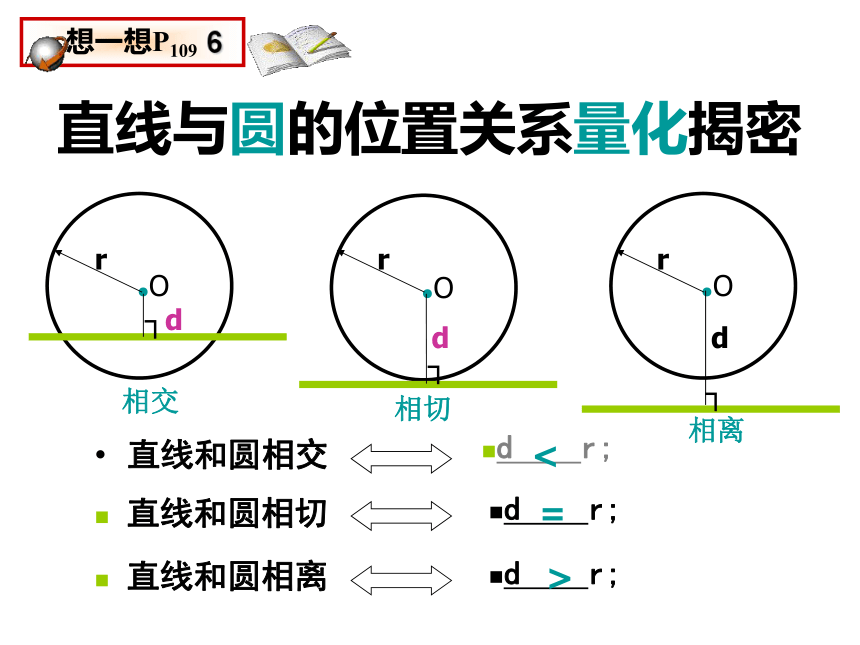
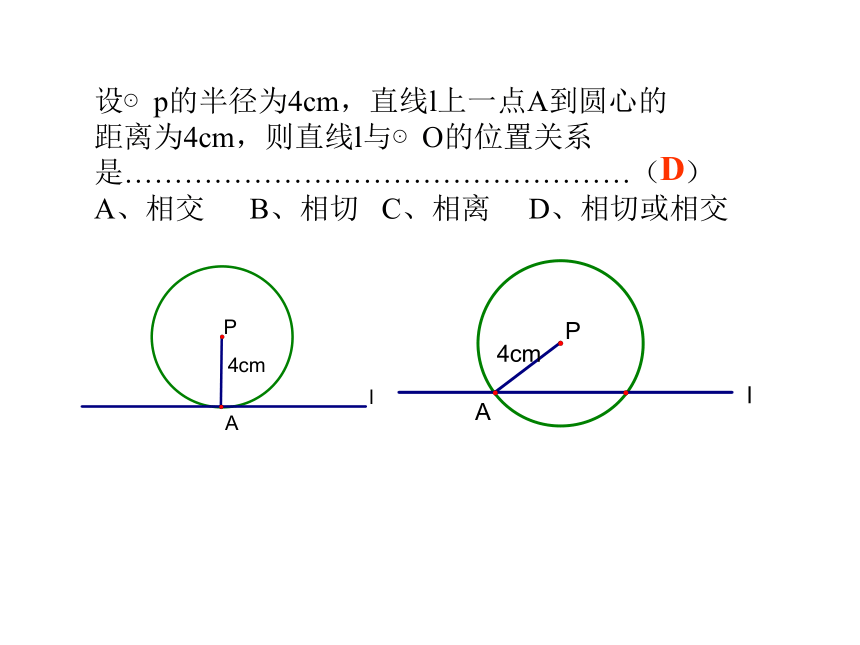
∴⊙P的半径r=4时, ⊙P与OA相切。练习题:已知∠AOB=300,OB上有一点P,OP=8cm,以P为圆心,____为半径作⊙P时,直线OA与⊙P相切。直线与圆的位置关系作一个圆,把直尺边缘看成一条直线.固定圆,平移直尺,直线和圆有哪几种位置关系?有三种位置关系:相交直线和圆有惟一公共点(即直线和圆相切)时,这条直线叫做圆的切线,这个惟一的公共点叫做切点.相切相离如图,圆心O到直线l的距离d与⊙O的半径r的大小有什么关系? 你能根据d与r的大小关系确定直线与圆的位置关系吗?直线与圆的位置关系量化揭密直线和圆相交d r;d r; 直线和圆相切 直线和圆相离d r;直线与圆的位置关系量化揭密<=>设⊙p的半径为4cm,直线l上一点A到圆心的
距离为4cm,则直线l与⊙O的位置关系
是……………………………………………( )
A、相交 B、相切 C、相离 D、相切或相交D探索切线性质1.你能举出生活中直线与圆相交,相切,相离的实例吗?2.上面的三个图形是轴对称图形吗?如果是,你能画出它们的对称轴吗?由此你能悟出点什么?探索切线性质如图,直线CD与⊙O相切于点A,直径AB与直线CD有怎样的位置关系?说说你的理由.直径AB垂直于直线CD.老师期望:
圆的对称性已经在你心中落地生根.小颖的理由是:
∵右图是轴对称图形,AB是对称轴,
∴沿直线AB对折图形时,AC与AD重合,因此,∠BAC=∠BAD=90°.探索切线性质小亮的理由是:直径AB与直线CD要么垂直,要么不垂直.假设AB与CD不垂直,过点O作一条直径垂直于CD,垂足为M,老师期望:
你能看明白(或掌握)用反证法说理的过程.则OM切线的性质定理是证明两线垂直的重要根据;作过切点的半径是常用经验辅助线之一.如图
∵CD是⊙O的切线,A是切点,OA是⊙O的半径,
∴CD⊥OA.若OC是⊙O的半径;AB⊥OC;
则直线AB切⊙O与C。(×)圆的切线的性质: (1)圆的切线垂直于过切点的半径; (2)经过圆心且垂直于切线的直线必过切点; (3)经过切点且垂直于切线的直线必过圆心. 按图填空:(口答)
(1). 如果AB切⊙O于A,
那么AOB⊙O的切线切点PA、PB分别切⊙O于A、BPA = PB∠OPA=∠OPB 从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角。 切线长定理几何语言: 外心:是指三角形外接圆的圆心内心:是指三角形内切圆的圆心三角形各边垂直平分线的交点三角形各内角角平分线的交点重心:是三角形各边中线的交点重心把每条中线内分成1:2的两条线段知 识 的 应 用若内切圆半径为r,则△ABC的面积为:(a+b+c) r/2r如图:直角三角形的两直角边分别是a,b,斜边为c 则其内切圆的半径为: : 弦切角的度数等于它所夹的弧度数的一半几何语言: BA切⊙O于A
AC是圆O的弦弦切角定理推论: 弦切角等于它所夹的弧对的圆周角∠BAC= ∠ADC相交弦定理 圆内的两条弦相交,被交点分成的两条线段长的积相等。相交弦定理的推论 如果弦与直径垂直相交,那么弦的一半是它分直径所成的两条线段的比例中项。从圆外一点引圆的切线,切线长是这点到割线与圆交点的两条线段的长的比例中项切割线定理:数学语言:
PT为⊙O切线,PAB为⊙O的割线
PT2 =PA ? PB割线定理从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段的长的乘积相等EF如图,OP=8,PC=1,PA=AB,
求PA。CDPA×PB=PC×PO
PA=2(×)PA×PB=PC×PD 过 圆外一点任意画圆的一条割线,这点到割线与圆的两个交点之间的两条线段长的乘积等于定值。设⊙ O的半径为 r ,PO=d当点P在圆内时, PA ? PB=( r - d )(r + d)
=当点P在圆外时 PA ? PB=(d-r)(d+r)
=由相交弦定理得:由割线定理得(圆内)点P在圆内,r>d,此时,P到A、B的距离的乘积为PA?PB=r2-d2点P在圆外,d>r,此时,P到A、B的距离的乘积为PA?PB=d2-r2PA?PB=| d2-r2 |切线的性质定理的应用1.已知Rt△ABC的斜边AB=8cm,直角边AC=4cm.(1)以点C为圆心作圆,当半径为多长时,AB与⊙C相切?老师提示:
模型“双垂直三角形”你可曾认识.解:(1)过点C作CD⊥AB于D.∵AB=8cm,AC=4cm.∴∠A=60°.因此,当半径长为 cm时,AB与⊙C相切.切线的性质定理的应用1.已知Rt△ABC的斜边AB=8cm,直角边AC=4cm.(2)以点C为圆心,分别以2cm,4cm为半径作两个圆,这两个圆与AB分别有怎样的位置关系?当r=4cm时,dr,AB与⊙C相离;解:(2)由(1)可知,圆心到AB的距离d= cm,所以切线的性质定理的应用1.直线BC与半径为r的⊙O相交,且点O到直线BC的距离为5,求r的取值范围..2.一枚直径为d的硬币沿直线滚动一圈.圆心经过的距离是多少?.老师提示:硬币滚动一圈,圆心经过的路经是与直线平行的一条线段,其长度等于圆的周长.挑战自我1.已知:如图,P是⊙O外一点,PA,PB都是⊙O的切线,A,B是切点.请你观察猜想,PA,PB有怎样的关系?并证明你的结论.2.由1所得的结论及证明过程,你还能发现那些新的结论?如果有,仍请你予以证明.老师提示:根据这个结论写出的命题称为切线长定理及其推论.5.直线和圆的位置关系(2)直线和圆相交d r;d r; 直线和圆相交直线和圆相交d r;直线与圆的位置关系量化揭密<=>画板演示切线的性质定理定理 圆切直线垂直于过切点的半径.如图∵CD是⊙O的切线,A是切点,OA是⊙O的半径,
∴CD⊥OA.老师提示:
切线的性质定理是证明两线垂直的重要根据;作过切点的半径是常用经验辅助线之一.直线何时变为切线如图,AB是⊙O的直径,直线CD经过点A,CD与AB的夹角为∠α,当CD绕点A旋转时,你能写出一个命题来表述这个事实吗?1.随着∠α的变化,点O到CD的距离如何变化?直线CD与⊙O的位置关系如何变化?2.当∠α等于多少度时,点O到CD的距离等于半径?此时,直线CD与⊙O有的位置关系?有为什么?切线的判定定理定理 经过半径的外端,并且垂直于这条半径的直线是圆的切线.老师提示:
切线的判定定理是证明一条直线是否是圆的切线的根据;作过切点的半径是常用经验辅助线之一.如图
∵OA是⊙O的半径,直线CD经过A点,且CD⊥OA,
∴ CD是⊙O的切线.切线判定定理的应用1.已知⊙O上有一点A,你能过点A点作出⊙O的切线吗?老师提示:
根据“经过半径的外端,并且垂直于这条半径的直线是圆的切线”只要连接OA,过点A作OA的垂线即可.2.已知⊙O外有一点P,你还能过点P点作出⊙O的切线吗?从一块三角形材料中,能否剪下一个圆,使其与各边都相切?老师提示:
假设符合条件的圆已作出,则它的圆心到三边的距离相等.因此,圆心在这个三角形三个角的平分线上,半径为圆心到三边的距离.三角形与圆的位置关系I●I●这样的圆可以作出几个?为什么?.∵直线BE和CF只有一个交点I,并且点I到△ABC三边的距离相等(为什么?),∴因此和△ABC三边都相切的圆可以作出一个,并且只能作一个.三角形与圆的位置关系三角形与圆的位置关系这圆叫做三角形的内切圆.这个三角形叫做圆的外切三角形.内切圆的圆心是三角形三条角平分线的交点,叫做三角形的内心.老师提示:
多边形的边与圆的位置关系称为切.四边形与圆的位置关系如果四边形的四条边都与一个圆相切,这圆叫做四边形的内切圆.这个四边形叫做圆的外切四边形.我们可以证明圆外切四边的一个重要性质:
1.圆外切四边形两组对边的和相等.三角形与圆的“切”关系1.以边长为3,4,5的三角形的三个顶点为圆心,分别作圆与对边相切,则这三个圆的半径分别是多少?.2.分别作出锐角三角形,直角三角形,钝角三角形的内切圆,并说明与它们内心的位置情况?老师提示:
先确定圆心和半径,尺规作图要保留作图痕迹.反思自我想一想,你的收获和困惑有哪些?说出来,与同学们分享.
思考:
观察上面直线与圆的位置情况,归纳一下共有几种不同的位置关系?
三种:
直线与圆没有公共点 (相离)
直线与圆只有一个公共点(相切)
直线与圆有两个公共点 (相交)那么如何来判断这三种位置关系呢?
1、已知的⊙O直径为5cm,直线L与圆心O之间的距离d。
(1)若d=2.5cm,则L与⊙O 有_______公共点,此时直线L与⊙O ___________.
(2)若d=3cm,则L与⊙O 有______公共点,此时直线L与⊙O __________.
(3)若d=1.5cm,则L与⊙O 有________公共点,此时直线L与⊙O __________.
2、 ⊙O 的半径R=4cm,弦AB=4√3cm,以点O为圆心,2cm为半径的圆和AB的位置关系是___________练习题:例题:Rt△ABC中,∠C=900,AC=3,BC=4,以C为圆心,2.5为半径作⊙C,问直线AB与⊙C的位置关系怎样?当半径为多少时,直线AB与⊙C相切?解:过顶点C作AB的垂线,垂足为D,则由勾股定理得AB=5,由面积关系得AC·BC=AB·CD,由此可求得CD=2.4。所以半径为2.5时,因为d
∴CP=1/2OP=4
∴⊙P的半径r=4时, ⊙P与OA相切。练习题:已知∠AOB=300,OB上有一点P,OP=8cm,以P为圆心,____为半径作⊙P时,直线OA与⊙P相切。直线与圆的位置关系作一个圆,把直尺边缘看成一条直线.固定圆,平移直尺,直线和圆有哪几种位置关系?有三种位置关系:相交直线和圆有惟一公共点(即直线和圆相切)时,这条直线叫做圆的切线,这个惟一的公共点叫做切点.相切相离如图,圆心O到直线l的距离d与⊙O的半径r的大小有什么关系? 你能根据d与r的大小关系确定直线与圆的位置关系吗?直线与圆的位置关系量化揭密直线和圆相交d r;d r; 直线和圆相切 直线和圆相离d r;直线与圆的位置关系量化揭密<=>设⊙p的半径为4cm,直线l上一点A到圆心的
距离为4cm,则直线l与⊙O的位置关系
是……………………………………………( )
A、相交 B、相切 C、相离 D、相切或相交D探索切线性质1.你能举出生活中直线与圆相交,相切,相离的实例吗?2.上面的三个图形是轴对称图形吗?如果是,你能画出它们的对称轴吗?由此你能悟出点什么?探索切线性质如图,直线CD与⊙O相切于点A,直径AB与直线CD有怎样的位置关系?说说你的理由.直径AB垂直于直线CD.老师期望:
圆的对称性已经在你心中落地生根.小颖的理由是:
∵右图是轴对称图形,AB是对称轴,
∴沿直线AB对折图形时,AC与AD重合,因此,∠BAC=∠BAD=90°.探索切线性质小亮的理由是:直径AB与直线CD要么垂直,要么不垂直.假设AB与CD不垂直,过点O作一条直径垂直于CD,垂足为M,老师期望:
你能看明白(或掌握)用反证法说理的过程.则OM
∵CD是⊙O的切线,A是切点,OA是⊙O的半径,
∴CD⊥OA.若OC是⊙O的半径;AB⊥OC;
则直线AB切⊙O与C。(×)圆的切线的性质: (1)圆的切线垂直于过切点的半径; (2)经过圆心且垂直于切线的直线必过切点; (3)经过切点且垂直于切线的直线必过圆心. 按图填空:(口答)
(1). 如果AB切⊙O于A,
那么AOB⊙O的切线切点PA、PB分别切⊙O于A、BPA = PB∠OPA=∠OPB 从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角。 切线长定理几何语言: 外心:是指三角形外接圆的圆心内心:是指三角形内切圆的圆心三角形各边垂直平分线的交点三角形各内角角平分线的交点重心:是三角形各边中线的交点重心把每条中线内分成1:2的两条线段知 识 的 应 用若内切圆半径为r,则△ABC的面积为:(a+b+c) r/2r如图:直角三角形的两直角边分别是a,b,斜边为c 则其内切圆的半径为: : 弦切角的度数等于它所夹的弧度数的一半几何语言: BA切⊙O于A
AC是圆O的弦弦切角定理推论: 弦切角等于它所夹的弧对的圆周角∠BAC= ∠ADC相交弦定理 圆内的两条弦相交,被交点分成的两条线段长的积相等。相交弦定理的推论 如果弦与直径垂直相交,那么弦的一半是它分直径所成的两条线段的比例中项。从圆外一点引圆的切线,切线长是这点到割线与圆交点的两条线段的长的比例中项切割线定理:数学语言:
PT为⊙O切线,PAB为⊙O的割线
PT2 =PA ? PB割线定理从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段的长的乘积相等EF如图,OP=8,PC=1,PA=AB,
求PA。CDPA×PB=PC×PO
PA=2(×)PA×PB=PC×PD 过 圆外一点任意画圆的一条割线,这点到割线与圆的两个交点之间的两条线段长的乘积等于定值。设⊙ O的半径为 r ,PO=d当点P在圆内时, PA ? PB=( r - d )(r + d)
=当点P在圆外时 PA ? PB=(d-r)(d+r)
=由相交弦定理得:由割线定理得(圆内)点P在圆内,r>d,此时,P到A、B的距离的乘积为PA?PB=r2-d2点P在圆外,d>r,此时,P到A、B的距离的乘积为PA?PB=d2-r2PA?PB=| d2-r2 |切线的性质定理的应用1.已知Rt△ABC的斜边AB=8cm,直角边AC=4cm.(1)以点C为圆心作圆,当半径为多长时,AB与⊙C相切?老师提示:
模型“双垂直三角形”你可曾认识.解:(1)过点C作CD⊥AB于D.∵AB=8cm,AC=4cm.∴∠A=60°.因此,当半径长为 cm时,AB与⊙C相切.切线的性质定理的应用1.已知Rt△ABC的斜边AB=8cm,直角边AC=4cm.(2)以点C为圆心,分别以2cm,4cm为半径作两个圆,这两个圆与AB分别有怎样的位置关系?当r=4cm时,d
∴CD⊥OA.老师提示:
切线的性质定理是证明两线垂直的重要根据;作过切点的半径是常用经验辅助线之一.直线何时变为切线如图,AB是⊙O的直径,直线CD经过点A,CD与AB的夹角为∠α,当CD绕点A旋转时,你能写出一个命题来表述这个事实吗?1.随着∠α的变化,点O到CD的距离如何变化?直线CD与⊙O的位置关系如何变化?2.当∠α等于多少度时,点O到CD的距离等于半径?此时,直线CD与⊙O有的位置关系?有为什么?切线的判定定理定理 经过半径的外端,并且垂直于这条半径的直线是圆的切线.老师提示:
切线的判定定理是证明一条直线是否是圆的切线的根据;作过切点的半径是常用经验辅助线之一.如图
∵OA是⊙O的半径,直线CD经过A点,且CD⊥OA,
∴ CD是⊙O的切线.切线判定定理的应用1.已知⊙O上有一点A,你能过点A点作出⊙O的切线吗?老师提示:
根据“经过半径的外端,并且垂直于这条半径的直线是圆的切线”只要连接OA,过点A作OA的垂线即可.2.已知⊙O外有一点P,你还能过点P点作出⊙O的切线吗?从一块三角形材料中,能否剪下一个圆,使其与各边都相切?老师提示:
假设符合条件的圆已作出,则它的圆心到三边的距离相等.因此,圆心在这个三角形三个角的平分线上,半径为圆心到三边的距离.三角形与圆的位置关系I●I●这样的圆可以作出几个?为什么?.∵直线BE和CF只有一个交点I,并且点I到△ABC三边的距离相等(为什么?),∴因此和△ABC三边都相切的圆可以作出一个,并且只能作一个.三角形与圆的位置关系三角形与圆的位置关系这圆叫做三角形的内切圆.这个三角形叫做圆的外切三角形.内切圆的圆心是三角形三条角平分线的交点,叫做三角形的内心.老师提示:
多边形的边与圆的位置关系称为切.四边形与圆的位置关系如果四边形的四条边都与一个圆相切,这圆叫做四边形的内切圆.这个四边形叫做圆的外切四边形.我们可以证明圆外切四边的一个重要性质:
1.圆外切四边形两组对边的和相等.三角形与圆的“切”关系1.以边长为3,4,5的三角形的三个顶点为圆心,分别作圆与对边相切,则这三个圆的半径分别是多少?.2.分别作出锐角三角形,直角三角形,钝角三角形的内切圆,并说明与它们内心的位置情况?老师提示:
先确定圆心和半径,尺规作图要保留作图痕迹.反思自我想一想,你的收获和困惑有哪些?说出来,与同学们分享.
同课章节目录
